2. 清华大学 网络科学与网络空间研究院, 北京 100084
2. Institute for Network Sciences and Cyberspace, Tsinghua University, Beijing 100084, China
当前, 数据被称为“新时代的石油”. 无论是在制定决策、预测分析等企业或组织的关键行为上, 还是在社交网络、电子商务等个人的日常生活上, 数据正扮演着越来越重要的角色. 随着云计算的蓬勃发展, 越来越多的企业将数据存储在云数据库上. 根据2022年12月13日Gartner发布的调研数据(https://www.gartner.com/doc/reprints?id=1-2AIUY4M7&ct=220707&st=sb), 整个DBMS市场在2021年强劲增长了22.3%, 达到803亿美元, 其中84%以上的增长来自云数据库平台即服务(dbPaaS). Gartner预测在dbPaaS的推动下整个DBMS市场规模将在2023年达到
• 2017年6月1日起施行《中华人民共和国网络安全法》.
• 2020年1月1日起施行《中华人民共和国密码法》.
• 2021年9月1日起施行《中华人民共和国数据安全法》.
• 2021年11月1日起施行《中华人民共和国个人信息保护法》.
这些法案的出台, 旨在保护组织和个人的数据安全, 加强对数据的保护和管理, 凸显了我国对数据安全的重视. 云数据库作为云计算的重要一环, 其安全性是至关重要的. 云数据库的安全性包括数据的机密性、完整性和可用性等. 机密性可以保护用户的敏感数据不被非授权方窥探和泄露. 在这样的背景下, 全密态数据库技术应运而生, 为敏感数据提供全生命周期的机密性保护. 全密态数据库可以将敏感数据加密, 只有拥有密钥才能够解密数据. 因此, 即使数据被窃取, 也不会泄露重要信息.
近年来, 全密态数据库的相关技术一直是学术界和工业界的研究热点. 本综述系统地对全密态数据库系统现有工作进行全面的调研与总结, 按照以下方式组织: 首先对全密态数据库的功能和挑战做了概述(见第1节). 其次介绍了全密态数据库的应用场景和3种典型架构(见第2节), 之后对3种架构的关键技术做了全面的总结和分析, 包括基于软件加密方案的关键技术(见第3节)、基于可信硬件TEE的关键技术(见第4节), 以及基于软硬融合的关键技术(见第5节). 然后对保护访问模式的相关技术做了总结和分析(见第6节). 最后对未来的研究趋势做了展望(见第7节).
1 全密态数据库概述全密态数据库可以为敏感数据提供全生命周期的机密性保护, 包括数据的密态传输、密态存储和密态计算. (1)密态传输: 通过TLS/SSL等技术, 将敏感数据以密文形式传输, 防止在传输过程中的泄露, 如网络抓包、IP/DNS欺骗等. (2)密态存储: 使用AES等加密算法, 将敏感数据以密文的形式存储在云数据库的磁盘上, 防止在存储介质上的泄露, 如物理存储设备丢失或被盗、数据库文件泄漏等. (3)密态计算: 利用加密算法或可信硬件, 使敏感数据在云端的非可信内存区域始终保持密文形式, 并完成相关的数据库操作. 密态计算可防止拥有服务器超级权限的数据库管理员窥探, 以及黑客复制内存快照或持续观测内存数据等攻击. 密态传输和密态存储的技术相对简单, 发展的已经比较成熟, 目前很多云数据库厂商都已支持这两项功能. 密态计算则相对复杂很多, 挑战较大, 是学术界和工业界近一二十年的研究热点, 并且还在持续研究. 因此全密态数据库的关键技术主要在密态计算部分, 本文主要介绍这部分的相关技术和典型研究工作.
全密态数据库的研究的挑战主要包含安全性、高性能和功能性3个方面. (1)安全性: 安全性是首要挑战. 安全性足够好的方案才能为敏感数据提供有效的机密性保护. 而失去了安全性, 则和普通数据库没有区别, 失去了全密态数据库的全部意义. 在基于软件加密算法的全密态数据库中, CryptDB (详见第3.8.1节)是较早提出的综合性方案, 支持大多数SQL查询并且性能较好. 但由于其使用了安全性较低的保序加密算法, 使得其整体安全性受到了很大的争议, 该方案也没有被工业界的数据库采用. (2)高性能: 现代数据库需要支持海量的数据和大并发、低延迟, 这对基于密文运算的全密态数据库提出了很高的性能挑战. 有的软件加密方案(例如全同态加密或混淆电路)既有很高的安全性, 又有很好的功能性(支持多种运算), 但由于性能很低, 往往没有可实践性, 仅处于理论研究阶段, 还不能应用在实际的数据库系统中. (3)功能性: 数据库, 尤其是关系型数据库, 包含很多复杂的运算, 包括等值查询、范围查询、字符串查询、连接、聚集等. 很多加密方案仅能支持这些运算中的一项或两项. 如何设计功能性更强的加密方案, 或组合多个加密方案构建安全高效的全密态数据库是一项挑战. 当前, 没有方案能够同时完美满足高安全性、高性能和高功能性. 往往高安全性、高功能性的方案, 性能极低; 而高功能性、高性能的方案, 安全性较低. 因此可实践的全密态数据库方案都需要在安全性、高性能和功能性三者之间做权衡(trade-off).
数据库经历了几十年的蓬勃发展, 衍生出多种不同类型. 从数据模型的角度看, 数据库可分为关系型数据库和非关系型数据库(文档型、键值型、图型等). 按照业务特征划分, 可分为事务型数据库和分析型数据库. 而从系统架构角度, 可分为集中式和分布式数据库等多种类别. 不同类型的数据库对全密态技术的需求有着显著差异. 通常情况下, 全密态数据库技术主要应用于需要极高数据隐私与安全性的场景, 例如医疗、金融和政府领域的数据库. 这些数据库多数属于关系型和事务型数据库. 因此, 全密态数据库的研究重点通常集中在这些类型的数据库上. 少数研究也涵盖了非关系型数据库, 如文档型数据库MongoDB、分析型数据库Monomi等. 近年来, 随着大数据的迅猛发展, 集中式数据库已无法满足巨大数据量的需求, 分布式数据库逐渐成为主流. 分布式关系型事务数据库对全密态技术的需求日益迫切. 然而, 由于全密态计算的复杂性, 目前的研究主要集中在集中式数据库领域. 有关现有全密态数据库类型的详细信息, 请参阅第3.8节和第4.2节.
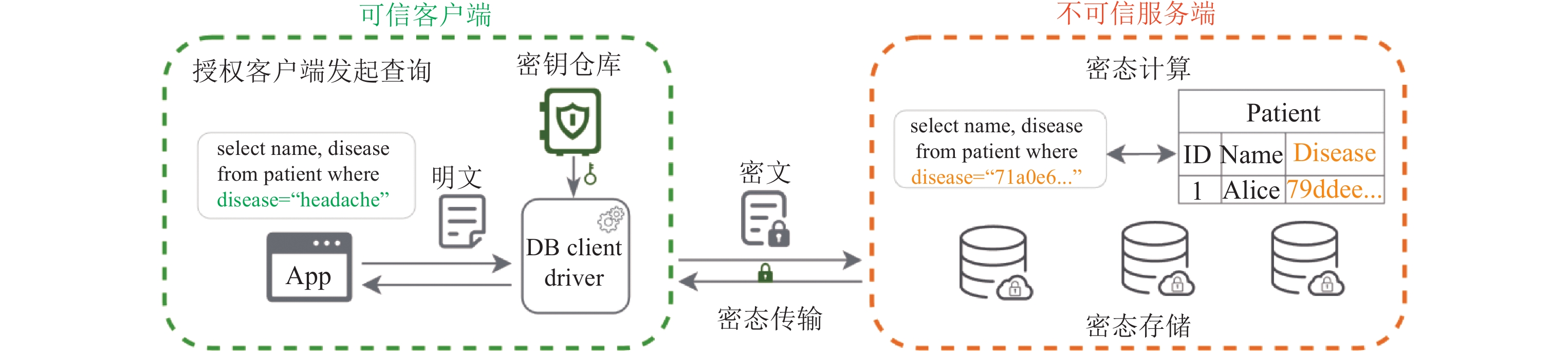
2 全密态数据库的模型和架构 2.1 全密态数据库系统模型全密态数据库的系统模型如如图1所示, 包含客户端和云服务端的两方场景. 客户端将数据外包给第三方云数据库服务端, 并以保护隐私的方式存储和检索. 客户端作为数据的拥有者和使用者是受信任方; 云服务端作为数据的存储和管理者, 是不受信任方. 在全密态数据库的场景下, 敏感数据只在授信方以明文形式存在. 当发送给非授信方时, 敏感数据被加密成密文传输, 并在非授信方始终以密文形式存储和计算. 具体地, 当客户端插入数据到服务端时, 敏感数据被数据库的客户端驱动程序(DB client driver)加密成密文再发送给服务端. 哪些数据字段(column或field)需要被加密成密文, 由该数据所在的数据库表或集合的schema决定. 加密所需要的密钥, 由密钥仓库提供给客户端驱动程序. 云服务端收到数据后, 以密文的形式存储到磁盘中. 之后, 当客户端检索数据时, 非可信的云服务端在密文上执行需要的数据库运算(例如, 等值查询、范围查询、多表连接, 聚合等), 并将查询结果以密文的形式返回给客户端. 客户端收到密文结果后, 由客户端驱动程序将其解密成明文. 客户端驱动程序的加密和解密操作可以做到自动完成, 对上层应用程序透明无感知. 由此, 敏感数据在离开可信区域之后, 始终以密文形式存在, 最大限度地保护数据的机密性.
|
图 1 全密态数据库系统模型 |
密钥服务用于密钥管理, 为客户端驱动程序提供加密所需要的密钥. 通常需要两类密钥: 数据加密密钥(data encryption key, DEK), 用来加密敏感数据; 以及用户主密(customer master key, CMK), 用来加密DEK. 加密后的DEK可以作为元数据(metadata)存储在云数据库内. 用户主密钥是最敏感的数据, 可以存储在用户本地或者可信的第三方密钥管理系统(key management system, KMS), 如AWS KMS、Azure Key Vault、华为云KMS、阿里云KMS等. 不同的数据库字段(column或field)可以使用不同的DEK加密, 通常在定义数据库表或集合时指定哪些字段需要加密, 以及加密的DEK ID, 这些信息保存在表或集合的元数据中. 客户端驱动程序可以从元数据里读取到这些配置, 完成自动加解密操作. 当需要加解密时, 客户端驱动程序向密钥仓库请求DEK, 密钥仓库从云数据库取到被加密的DEK, 用CMK解密后发送给客户端驱动程序做数据的加解密操作. 除了数据加密密钥和用户主密钥, 有的全密态数据库系统(如GaussDB)还设计了用户侧的设备密钥, 构成3层密钥体系. 设备密钥用于实现用户侧客户端设备之间的加密隔离, 进一步提升整体的安全性, 详细介绍见第5节.
2.2 全密态数据库的敌手模型敌手模型(adversary model)也被称为攻击模型(attack model)或威胁模型(threat model), 用于定义和分析给定系统或场景中的潜在对手或攻击者, 可以帮助研究人员了解潜在攻击者的目标、能力和资源, 有助于设计安全系统和制定有效的对策. 敌手分为被动型敌手(passive adversaries)和主动型敌手(active adversaries)两种类型[1]. 被动型敌手通常具有非法监听或读取数据的能力, 但没有篡改数据的能力, 因此又被称为诚实且好奇型敌手(honest-but-curious adversaries)或半诚实型敌手(semi-honest adversaries). 而主动型敌手不仅拥有非法监听或读取的能力, 还可以对数据做篡改, 因此也被称为恶意型敌手(malicious adversaries).
敌手模型是衡量全密态数据库设计有效性的关键因素. 很多研究将云数据库服务端假设为半诚实型敌手(被动型敌手), 即用户的敏感数据在服务端可能会被窥探或泄露, 并会假设敌手不仅能够将内存中的敏感数据以快照的形式导出, 还具有持续观察内存中数据实时变化的能力, 包括内存的访问模式. 对于这种情况, 研究的重点是如何保护数据的机密性, 即敏感数据的明文信息不会被泄露; 也有一些研究将云服务端假设为恶意型敌手(主动型敌手), 即敏感数据不仅可能会被窥探、泄露, 甚至可能会被恶意篡改或删减. 此时, 不仅要保护数据的机密性, 还需要对云服务端返回的数据做正确性与完整性校验. 此外, 全密态数据库通常会和传统的数据库安全机制结合起来使用, 如安全认证机制、访问对象控制、用户角色管理、审计机制等, 以达到更全面的安全效果. 有关现有全密态数据库的敌手模型的详细信息, 请参阅第3.8节和第4.2节.
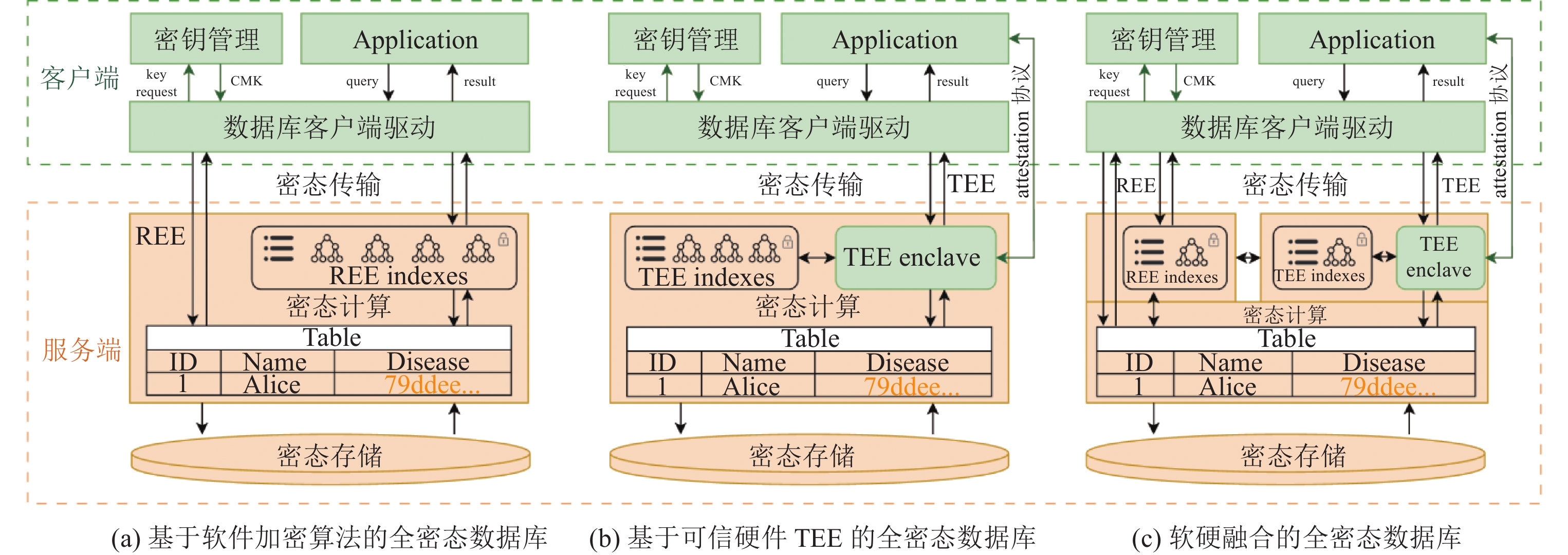
2.3 全密态数据库的3种典型架构全密态数据库有3种典型的架构(如图2所示).
|
图 2 全密态数据库的3种典型架构 |
(1) 基于软件加密算法的全密态数据库
基于加密算法的全密态数据库运行在传统的非可信富执行环境(rich execution environment, REE)中, 依赖纯软件的加密算法实现密文上的数据库操作. 例如, 使用确定性加密算法实现等值查询, 使用保序加密算法实现范围查询等. 确定性加密算法和保序加密算法的性能较高, 但安全性较低. 确定性加密算法暴露了密文的重复次数, 保序加密算法则暴露了密文的顺序. 此外确定性加密只适用于等值查询, 保序加密只适用于范围查询.
基于加密算法的全密态数据库的挑战在于如何安全、高效地在密文上实现各种数据库操作. 由于加密算法需要较大的计算资源和存储资源, 往往安全性高的算法性能低(例如同态加密算法), 性能高的算法安全性低(例如保序加密算法), 安全性和性能都高的算法功能性差(例如随机加密算法). 目前还没有任何一个加密算法能够同时满足高安全性、高性能和高功能性. 因此, 设计加密算法时, 经常需要在安全性、功能性和性能三者之间做权衡(trade-off).
(2) 基于可信硬件TEE的全密态数据库
这类全密态数据库依赖可信执行环境(trusted execution environment, TEE)实现数据库密态操作. 主流的可信执行环境有Intel SGX, AMD SEV, ARM TrustZone等, 微软的Always Encrypted [2]和阿里云的Enclage[3]基于Intel SGX实现. TEE在云服务端开辟了一小块可信区域, 被称为飞地(enclave), 用于保护敏感数据和关键代码. 飞地可以被看作是客户端的一部分, 是客户端在云服务端的延伸. 因此, 飞地是可信的, 敏感数据在飞地内可以是明文形式, 而在飞地之外则总是处于加密状态. 通过远程认证(attestation)协议, TEE能够从客户端取得密钥, 进而解密进入到飞地内的密文数据, 并在解密后的明文上执行各种数据库操作, 再将得到的结果加密, 返回给客户端. 不过飞地的内存空间是有限的, 而且TEE与REE之间通讯的上下文切换开销十分高昂. 因此, 将数据库集成到TEE并构建可信计算系统是一项挑战. 具体地, 首先是如何合理地拆分数据库系统的功能, 将哪些部分放到TEE内执行, 哪些留在REE内执行; 其次, 对于需要放到TEE内的数据, 如何设计合适的数据粒度、如何与REE交互; 再次, 如何减少TEE和REE之间的高昂的交互开销.
与软件加密算法相比, TEE最大的优点是能够在明文上做各种数据库运算, 因此功能性和性能都更好. 此外, 不同于一些加密算法只能支持部分数据库操作(如等值查询, 范围查询等), 基于明文运算的TEE几乎可以支持所有的数据库操作, 这大大降低了全密态数据库的设计复杂度和开发成本. 目前工业界主流的全密态数据库大多都支持了TEE的实现, 例如微软的Azure[2]、阿里云的PolarDB[3]、华为云的GaussDB[4]等. 相比软件加密算法, TEE泄漏的信息更少, 安全性也更高. 不过, TEE并非绝对安全, 仍然会受到如侧信道攻击等方式的攻击. 如果设计上存在缺陷或漏洞, 修复成本高昂且十分依赖于硬件厂商. 早期的TEE几乎都源自国外厂商的产品, 近几年国内的芯片厂商如海思、海光、兆芯、飞腾等也纷纷推出了自主可控的TEE产品, 为关系到国计民生的数据安全提供了有力保障.
(3) 软硬融合的全密态数据库
软硬融合的全密态数据库融合了软件加密算法和可信硬件TEE双方的优点, 将部分查询操作利用加密算法和REE加密索引在REE下执行, 部分操作利用可信硬件和TEE加密索引在TEE下执行, 显著地降低REE和TEE之间的交互开销. REE加密索引和TEE加密索引都是基于密文或加密索引值构建出来的索引. 他们的主要区别在于, REE加密索引的构建和查询依赖于加密算法, 运行在具有更多计算资源的REE中; 而TEE加密索引则依赖于TEE飞地将密文解密成明文, 并在明文上进行计算. 软硬融合架构的主要挑战在于如何正确地选择和分配TEE与REE中的查询操作, 以降低执行开销. GaussDB[4]是软硬融合的全密态数据库的典型代表.
表1给出了3种全密态数据库架构的横向对比. 其中, 基于软件加密算法的全密态数据库, 仅考虑目前具有可实践性的加密方案. 此外, 后3列中的“高”“中”“低”这3个指标是这3种架构之间相互比较的相对值. 有关这3种架构相关技术的详细信息, 请参阅第3节、第4节和第5节.
| 表 1 全密态数据库3种典型架构对比 |
3 基于加密算法的全密态数据库关键技术
基于软件加密算法的全密态数据库仅依赖加密算法实现密文上的各种数据库操作, 包括明文加密、等值查询、范围查询、字符串查询、算术运算等. 由于不需要依赖硬件设备, 这类全密态数据库可以运行在一般的云主机上, 有较好的通用性. 不过, 加密算法通常在功能性上存在局限, 如随机加密仅适用于明文加密, 确定性加密仅适用于等值查询, 保序加密仅适用于范围查询等. 因此, 基于软件加密算法的全密态数据库系统需要组合使用多种加密算法, 来实现较完整的数据库功能. 表2对全密态数据库的操作和对应的加密算法做了概括和分类.
| 表 2 全密态数据库操作类型与适合该操作的加密算法分类 |
3.1 加密算法的安全性
我们首先对加密算法的安全性做简要的介绍, 以便更好地说明各加密算法的安全性. 1982年Goldwasser等人[11]首次提出了语义安全(semantic security)的概念. 对于一个加密算法, 如果它的密文不会泄漏明文的任何信息, 或者根据密文来识别明文在概率上是可忽略的(negligible), 那么该加密算法是语义安全的. 语义安全概念在直觉上很容易理解, 不过不便于在计算机环境下描述和证明. 密码学家们于是提出了一种基于猜测游戏的安全性定义. 该游戏假定有一个敌手(adversary)和一个挑战者(challenger). 敌手宣称攻破了某个加密算法, 挑战者表示怀疑并向敌手发起挑战. 为了便于理解, 我们将游戏分为观察阶段和猜测阶段. 在观察阶段, 敌手可以在约定的限制条件下观察加密算法. 敌手会选择不同类型的数据, 如明文、密文、关键词等, 发送给挑战者. 挑战者拥有密钥, 可以将敌手发来的数据做加密或解密操作, 再将结果发送给敌手观察. 观察阶段可以持续多项式时间. 在猜测阶段, 敌手将两个相同长度的明文m0和m1发送给挑战者. 挑战者随机选择
工业界早期的全密态数据库仅能够支持极少的密态操作, 如MongoDB在2019年4.2版本中发布的Client-side field level encryption功能[13], 只支持明文加密, 而不能基于密文做任何查询操作, 需要通过其他非加密字段查询加密的敏感数据. 明文加密通常采用随机加密算法(randomized encryption, RND), 例如随机初始化向量的AES-CBC算法. 随机加密算法将明文加密成随机的密文, 即使相同的明文也会被加密成完全不同的密文, 因此有较高的安全性IND-CPA. 但同样因为加密是完全随机的, 无法仅根据密文做任何查询操作. 因此随机加密算法仅适合为安全性要求很高的敏感数据做加密, 通过其他非加密字段来检索加密的敏感数据.
3.3 密态等值查询 3.3.1 基于确定性加密的等值查询确定性加密算法(deterministic encryption, DET), 如固定初始化向量的AES-CBC算法, 将明文加密成确定性的密文, 即相同的明文总是被加密成相同的密文. 这个特性使得确定性加密算法很适合密态等值查询、等值连接、聚集等操作. 但这样暴露了相同明文的重复频率, 继而暴露了密文的分布规律, 因此安全性较低(IND-DCPA). 确定性加密容易受到推理攻击(inference attack), 尤其是对于数据分布可能存在规律的敏感数据集合(例如性别、年龄等). 攻击者可以根据密文的分布规律结合该数据集的统计信息推测出大量明文信息. Naveed 等人[5]通过推理攻击, 在200家美国医院的电子病历加密数据和公开可用的辅助信息基础上, 推断出超过60%的医院的60%以上的确定性加密数据, 包括性别、种族和死亡风险. 因此确定性加密算法仅适合于安全性要求不高、统计信息不明显, 并且有等值查询需求的敏感信息. 很多工业界的全密态数据库在早期使用确定性加密算法实现等值查询, 如微软的Azure[2]、阿里的PolarDB[3]、华为的GaussDB[4]等.
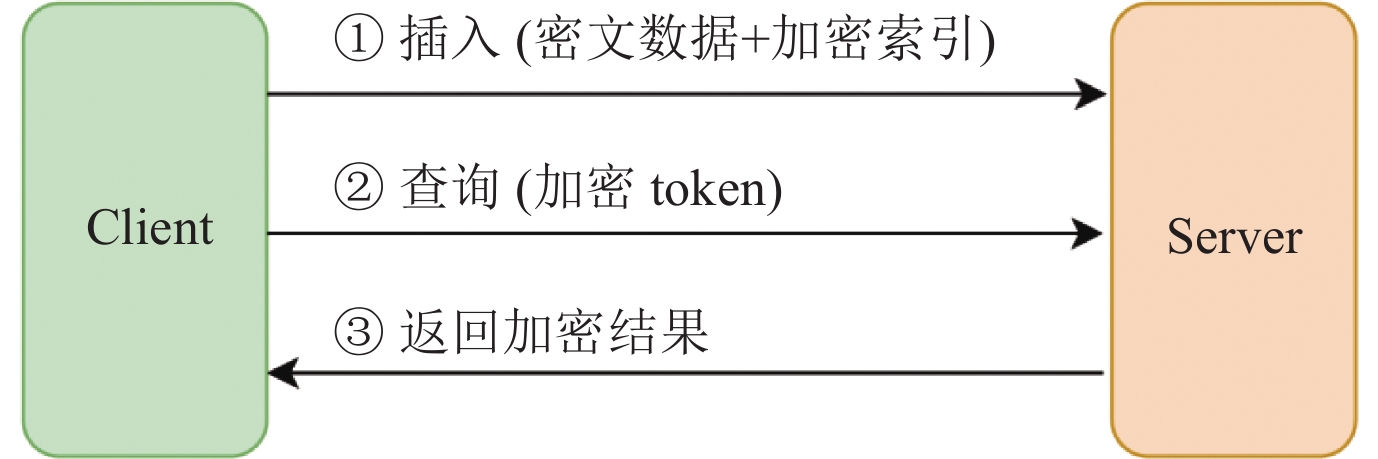
3.3.2 基于对称可搜索加密的等值查询可搜索加密(searchable encryption, SE)[14−33]是密文搜索领域的研究热点, 使得数据拥有者(客户端)可以将敏感数据外包到不受信任的云服务端加密存储, 并仍然可以根据关键词检索加密的数据. 可搜索加密广泛应用于医疗、政务、电子邮件等云服务场景. 不同于基本的加密算法(如RND, DET), 可搜索加密是由基本加密算法构建而成的加密方案(scheme). 图3展示了其主要流程特征[25,31]: (1)当插入数据时, 客户端将明文加密成随机密文, 同时也为明文生成加密索引(除了方案[14]), 并将密文和加密索引发送给云服务端存储. (2)当搜索某个关键词时, 客户端为该关键词生成陷门(trapdoor, 也称为token[31]), 发送给服务端. (3)服务端基于陷门在加密索引上查找包含该关键词的加密数据, 并将匹配的加密数据返回给客户端.
|
图 3 可搜索加密 (SE) |
对称可搜索加密(searchable symmetric encryption, SSE)[14,16,18−24,29,32]是可搜索加密的一个重要分支, 其使用对称加密算法(例如AES算法)加密敏感数据, 性能上好于使用公钥加密算法的非对称可搜索加密(asymmetric symmetric encryption, ASE). 并且, 对称可搜索加密适用于数据的拥有者和使用者为同一方的全密态数据库两方场景, 而非对称可搜索加密适用于数据拥有者和使用者不是同一方的数据共享多方场景. 2000年Song等人[14]首次提出了可搜索加密的概念, 并构造了首个对称可搜索加密方案SWP, 其具有IND-CPA安全性[21]. 但该方案只加密了文档, 没有生成加密索引. 每次查询需要完整地遍历所有的加密文档, 搜索时间与加密文档的个数和大小成正比, 因此效率较低. 除Song 等人[14]的SWP方案外, 其他可搜索加密方案都设计了加密索引, 如倒排索引[21]、正排索引[15]、树形索引[33,34]、布隆过滤器索引[35]等. 多种类型的索引使得SSE算法有非常广泛的适用性, 使用正排索引和倒排索引的SSE算法可支持密态等值查询, 使用树形索引的SSE可支持密态范围查询(详见第3.4节), 使用布隆过滤器索引的SSE可支持密态字符串通配符查询(详见第3.5节).
3.4 密态范围查询 3.4.1 基于分桶的密态范围查询2002年Hacigümüş 等人[36]利用分桶的方法设计了一个整数范围查询加密方案. 其核心思想是将敏感属性的值域空间划分成若干个分区(桶). 插入数据时, 客户端将每个元组整体加密, 并为其中的为每个敏感属性值分配桶ID, 发送到服务端. 假设一个明文关系表包含3个敏感属性列, 那么该表在服务端会被保存为4列, 第1列为加密的元组密文, 后3列分别是3个敏感属性的桶ID列, 即3个加密索引. 查询时, 查询条件里的常数会被替换成对应的桶ID (可能是多个), 再发送给服务端检索, 并返回结果. 这个方案的一个很明显的缺点是查询结果会有错误命中(假阳)数据, 需要客户端在收到密文结果后做后处理(post-processing)操作, 解密密文并过滤掉假阳数据. 由于桶ID可能会参与连接、子查询等运算, 过滤过程可能会相当复杂. 假阳的数量取决于分区的宽度, 设计合适的分区宽度是一项挑战. 文献[36]中显示, 当分区的宽度过大时, 后处理的开销可能会变得极大. 而分区宽度过小时, 容易暴露明文信息, 尤其是当分区等宽的时候.
2004年Hore等人[37]在Hacigümüş 等人[36]的方案基础上做了改进, 给出了设置合理分区大小的优化算法, 减少查询处理中的性能开销. 该算法还允许数据拥有者(客户端)微调分桶大小, 通过牺牲少量的查询准确性(包含一定的假阳数据)来实现所需的数据隐私级别. 2012年Hore等人[38]又在之前工作的基础上将一维的分桶索引推广到多维分桶索引, 以更高效地支持多维范围查询.
分桶方案都基于确定性加密算法(DET), 将范围查询转换成多个桶的等值查询, 是一种有效的查询方案. 但同时也继承确定性加密暴露相同明文重复频率的缺点, 暴露了被查询数据的分区分布. 并且分桶方案都没有给出严格的安全性定义和证明, 这使得很难确定其他可能的泄漏. 从密码学角度来说, 存在一定的安全隐患.
3.4.2 基于保序加密的密态范围查询保序加密(order preserving encryption, OPE)[39−46]使得密文保持了明文的顺序属性, 并且明文和密文都是数字类型的数据. 例如, 如果明文x<y, 那么对应的密文OPEK(x)<OPEK(y). 这个特性对数据库非常友好, 可以直接基于密文构建B-tree索引, 而无需改动现有任何功能, 并且查询效率很高. 但保序加密算法暴露了明文的顺序, 并且大部分保序加密算法是确定性的, 暴露了相同明文重复频率, 容易受到推理攻击, 因此安全性较低. 保序加密算法的发展可按其到达的安全性分为4个阶段[47]: (1)无严格安全性; (2)严格安全性; (3)理想安全性; (4)超越理想安全性.
(1) 无严格安全性定义的保序加密方案
2004年由Agrawal等人[39]在数据库社区(SIGMOD 2004)首次正式提出保序加密的概念, 并给出了第1个保序加密构造方案. 其基本思想是将所有明文数据和用户提供的目标分布(如高斯分布、均匀分布等)作为输入, 并以保持顺序的方式转换明文值, 转换后的值(即密文)遵循目标分布. 该方案在功能上有一定的局限性, 它的加密算法必须将数据库中的所有明文作为输入, 这是一种有状态的构造方式, 即加密某一个明文时, 需要依赖其他明文的加密状态. 而现实中的数据库中的数据大多是动态增长的, 无法事先知道所有明文, 因此无状态的动态加密方案更有实践性. 安全性方面, 该方案是确定性的, 暴露了相同明文的重复频率, 敌手可以使用重复项来猜测明文值域的分布, 尤其是在分布高度倾斜或明文值域中不同值的数量很少的情况下(例如, 一个月中的某天). 此外, Agrawal等人没有给出该方案的严格安全性定义, 也没有提供正式的安全性分析. Boldyreva等人[40]从密码学的角度认为该方案的安全性隐患较大.
(2) 有严格安全性定义的保序加密方案
2009年Boldyreva等人[40]从密码学的角度给出了保序加密的安全性定义. Boldyreva等人认为保序加密理论上的理想安全性是密文不会暴露明文除顺序以外的任何信息. 并仿照确定性加密为敌手增加限制的方式, 将保序加密的理想安全性定义为有序的选择明文攻击下的不可区分性(indistinguishability under ordered chosen-plaintext attack, IND-OCPA), 即限定敌手选择的明文都是顺序递增或递减的. 同时, Boldyreva等人也证明在加密算法无状态(stateless)和密文不变(immutable)的前提下, 要达到IND-OCPA安全性需要密文的长度随明文长度呈指数级增长, 这超出了计算机多项式级的处理能力, 是不可实践的. 无状态是指加密新的明文时无需参考之前加密的明文密文映射关系. Boldyreva等人给出了在无状态、密文不变条件下的较弱的安全性定义, 即抗选择密文攻击的伪随机保序函数(pseudorandom order-preserving function against chosen-ciphertext attack, POPF-CCA), 并基于伪随机函数(PRFs)和伪随机置换(PRPs)设计了符合POPF-CCA安全性的保序加密方案. 该方案依然是确定性的, 会暴露相同明文的重复频率, 容易受到推理攻击. 功能性方面, Boldyreva等人的方案是无状态的, 加密明文时无需依赖之前被加密的密文分布, 适合现实中动态增长的数据库场景. 此外, Boldyreva等人认为该方案是高效的(Boldyreva等人将“高效”定义为时间复杂度随数据规模的增长呈对数级(logarithmic)或者亚线性级(sub-linear)), 并给出其加密的时间复杂度为 log(M)–1和log(M)之间, 其中M为明文的数据规模.
(3) 理想安全性的保序加密方案
2013年Popa等人[43]提出了一个有状态(stateful)、密文可变(mutable)、交互式(interactive)的OPE方案, 是首个达到了理想安全性IND-OCPA的OPE方案, 并且Popa等人给出了严格的安全性证明. 该方案的基本思想基于非常自然的想法, 即直接使用明文的顺序编号作为保序密文值, 这样密文就只包含明文的顺序信息, 而不会泄漏任何其他信息. 例如, 对于3个明文{1, 5, 3}, 它们对应的保序密文可以为{1, 3, 2}. 当加密一个新的明文4时, 需要参考之前的明文密文对应关系(状态), 并按需调整之前的密文值. 按照明文的顺序, 需要将明文4的密文设置为3, 而明文5的密文需调整为4. 因此明文序列{1, 5, 3, 4}对应的密文序列为{1, 4, 2, 3}. 有状态和密文可变的保序加密方案牺牲了一部分存储空间和性能来实现理想安全性. Popa等人在服务端构建了一个二叉搜索树来维护保序密文. 当发生增删改查操作时, 客户端都需要与服务端交互来遍历搜索树, 最坏可能会产生搜索树的层高次的交互. 考虑到在云数据库的场景, 客户端与服务端通常不在一个局域网内, 多次交互将产生极大的网络延迟. 此外, 为了减少层高, 二叉搜索树最好为平衡二叉树, 使得在相同的数据规模下层高最小. 这就要求随着数据的插入和更新, 搜索树需要做再平衡(rebalance)处理, 也大大增加了维护开销. 因此, 该方案的性能较差, 不具有可实践性.
虽然Popa等人的方案达到了OPE的理想安全性IND-OCPA, 但由于密文是确定性的, 暴露了相同明文的重复频率, 依然容易受到推理攻击[5]. 例如, 对于考试分数为[0, 100]这样的数据集, 攻击者可以对密文去重, 得到互不相同(distinct)的密文. 当互不相同的密文数据足够多, 达到101个时, 攻击者就可以依据密文的顺序将密文和明文[0, 100]一一对应, 此时明文信息被完全暴露了. 因此暴露明文重复频率的OPE算法依然不够安全, 之后又有人提出隐藏频率的OPE算法, 可以称之为超越理想安全性的OPE算法.
(4) 超越理想安全性的保序加密方案
2015年Kerschbaum等人[48]提出了隐藏频率的OPE方案(frequency-hiding order-preserving encryption, FH-OPE). 该方案不仅达到了理想安全性IND-OCPA, 并且隐藏了相同明文的重复频率, 因此其安全性超越了理想安全性, 优于之前的所有OPE加密算法. Kerschbaum等人将这种安全性定义为频率分析有序选择明文攻击下的不可区分性(indistinguishability under frequency-analyzing ordered chosen-plaintext attack, IND-FAOCPA). 该方案的基本思想是在客户端构建树形索引来映射明文和非确定性保序密文, 每次查询仅有一次交互. 不过, 该方案理论上虽然可行, 但需要在客户端保存大量明文和密文映射数据, 其存储开销与数据规模呈线性增长, 因此不具有可实践性.
2021年Li等人[46]提出了另一个FH-OPE方案, 与Kerschbaum等人[48]的方案类似, 在客户端存储明文和非确定性密文的映射数据, 但存储开销有所改进, 只与不同的(distinct)明文线性相关, 即重复的明文不会增加存储开销. 并且该方案每次查询也仅有一次交互. 该方案适合值域空间不大的数据集合, 比如考试分数、一个月中的某天等. 对于值域空间较大的数据集合, 存储开销依然较大.
表3对保序加密方案做了对比, 其中n为加密数据集合总大小, N为加密数据集中互不不同的数据个数.
| 表 3 保序加密方案对比 |
3.4.3 基于揭序加密的密态范围查询
揭序加密(order-revealing encryption, ORE)[49−53]是对早期保序加密算法的改进, 在提高安全性的同时仍然能够判断密文的顺序. 与OPE密文能够直接判断顺序不同, ORE密文需要通过比较函数来判断顺序. 并且ORE的密文不需要像OPE密文那样只能是数字. 此外, ORE算法都是无状态的, 密文不会改变, 也不需要交互. 不过ORE也是确定性的, 其密文没有隐藏相同明文的重复频率.
2015年Boneh等人[50]首次提出了ORE概念, 并设计了首个ORE方案. 该方案基于多线性映射(multilinear map), 达到了等价于IND-OCPA的安全性. 但多线性映射是一种非常复杂的密码学工具, 效率很低, 因此该方案理论上可行, 但目前不具有实用性.
2016年Chenette等人[51]提出了基于伪随机函数的可实践的ORE方案, 其密文长度只有明文长度的1.6倍, 是目前性能最高的ORE方案, 但安全性没有达到IND-OCPA. 如前面所述, Boldyreva等人[40]证明过在无状态和密文不变的前提下, 达到IND-OCPA是不可实践的. Chenette等人的方案除了暴露了明文的顺序之外, 还泄露了密文的第1个不相同比特的位置. Chenette等人认为这是一种有限的泄露(limited leakage), 是可接受的. 不过文献[49]指出第1个不同的比特位置会暴露两个值的大概距离.
为了进一步减少信息泄露, 2016年Lewi等人[52]提出了两个基于分块(block)的ORE方案, 一个用于小明文值域的Lewi-Wu-Small, 一个用于正常明文值域的Lewi-Wu-Normal. Lewi-Wu-Small只泄露了顺序, 安全性达到了IND-OCPA, 但由于它是无状态的, 密文长度随明文呈指数级增长. Lewi-Wu-Normal泄露了第1个不同的block, 安全性没有达到IND-OCPA, 不过其安全性好于Chenette等人[51]的方案. 但安全性的提高牺牲了性能, 文献[49]指出随着block得增大, 性能会呈指数级下降.
2022年Liu等人[53]提出了一个新的ORE方案EncodeORE, 进一步减少了泄露的信息, 并保持了密文长度和加密时间的实用性. Liu等人[53]的动机是融合Chenette等人[51]和Lewi等人[52]两个方案的优点, 将密文分为两个部分left part和right part. Left part是一个小的值域, 代表明文的范围, 由Lewi-Wu-Small构建, 其安全性较高. Right part代表值域内的相对值, 由Chenette等人[51]的方案构建. 通过这样的方式将比较操作改为了范围比较和值比较, 进一步减少了泄露的信息. 但由于Lewi-Wu-Small的方案有密文膨胀问题, 实现时改用科学计数法表示明文. Liu等人设计了一个算法将科学计数法形式的明文编码成range part和value part, 再用Chenette等人[51]的方案加密两个部分, 使他们都可以做比较操作. 这个方案被命名为EncodeORE. 虽然不能用Lewi-Wu-Small实现, 安全性上有损失, 但依然好于Lewi-Wu-Normal的安全性. 并且基于Chenette等人[51]的方案完成比较操作, 因此继承了其较好的性能.
表4给出了上述揭序加密方案的对比, 其中n为明文长度. Lewi-Wu-Normal的d为block长度, λ为伪随机函数的输出长度. EncodeORE的l1是value pard的长度, l2是range part的长度. 我们可以看出, ORE方案的安全性不一定都优于OPE方案. 在2015年Boneh等人[50]首次提出了ORE方案时, ORE安全性达到了理想安全性IND-OCPA, 优于当时未达到理想安全性的OPE方案. 但之后OPE不断优化出安全性更高的方案. 对比达到的最高安全性, OPE达到的IND-FAOCPA要高于ORE达到的IND-OCPA.
| 表 4 揭序加密方案对比 |
虽然部分OPE和ORE方案都实现了除了顺序不暴露任何明文的其他信息, 有些还隐藏了等值频率信息, 但暴露顺序本身就令其安全性大大降低. 比如, 如果被加密的列是考试成绩或者工资等有一定分布规律的数据, 那么攻击者能通过密文顺序来观察其分布规律, 再结合公开的统计信息, 就能推断出大量明文信息. 一系列攻击[5,8,54]表明, 给定某些辅助信息, 攻击者可以从OPE和ORE方案揭示的顺序和相等关系中提取重要的敏感信息. 其中Naveed等人[5]通过推理攻击(inference attack), 在200家美国医院的电子病历加密数据和公开可用的辅助信息基础上, 推断出了超过95%的医院的80%以上的确定性加密数据.
3.4.4 基于对称可搜索加密(SSE)和树形索引的密态范围查询基于对称可搜索加密(SSE)和树形索引的方案的核心思想是利用树形索引将范围查询转变成了多个SSE token的等值查询. 通常用树形索引表示一个值域(例如32位非负整数), 每个叶子节点代表值域里的一个值, 每个中间节点代表包含其所有下层节点的范围, 根节点代表整个值域空间. 当插入数据时, 客户端生成随机密文的同时, 按照树形结构生成相关节点的加密索引值, 发送到服务端存储. 当查询某个范围时, 客户端按照树形结构将这个范围转换成多个相关节点的集合, 并生成对应的token集合, 发送给服务端. 服务端在加密索引里查找与token集合匹配的结果, 返回给客户端.
2016年Demertzis等人[34]提出了基于SSE和树形索引的一维范围查询RSSE框架, 将范围查询转换成多个子范围关键词的等值查询. 对于一个给定的查询范围, 如何将其按照树形结构拆分成多个子范围, Demertzis等人给出了4个方案: (1) Logarithmic-BRC, 使用最佳范围覆盖算法(best range cover, BRC)拆分查询范围. 对于给定的查询范围, BRC将其拆分为正好覆盖该查询范围, 并且没有重叠、没有假阳数据的子范围集合. (2) Logarithmic-URC, 使用统一范围覆盖算法(uniform range cover, URC), 将相同大小的查询范围拆分成统一大小的子范围集合. (3) Logarithmic-SRC, 使用单一范围覆盖算法(single range cover, SRC), 无论查询范围多大, 都会被转换成包含该范围的一个更大的范围. 隐藏了子范围的个数, 但结果可能会包含大量假阳数据. (4) Logarithmic-SRC-i, 在Logarithmic-SRC的基础上, 通过将树形结构每两个相邻的中间节点之间再增加一个节点, 将假阳的数据量从Logarithmic-SRC的O(n)降低为O(R+r), 其中n为数据库大小, R为请求的范围大小, r为返回结果的大小.
2022年Falzon等人[33]将基于SSE和树形索引的密态范围查询, 从一维扩展为多维, 并给出了严格的安全性证明. 其基本思想与Demertzis等人[34]的一维方案比较相似, 为了支持多维密态范围查询, Falzon等人引入了一个通用框架, 通过空间索引(多维范围树、四叉树)构建密态范围查询方案, 将目标范围查询转换为对底层加密multimap的一组查询.
与OPE和ORE相比, 基于SSE和树形索引的密态范围查询的安全性可达到自适应选择关键词下的不可区分性(adaptive indistinguishability against chosen keyword attack, IND-CKA2), 高于OPE和ORE的IND-OCPA, 低于随机加密算法的IND-CPA, 属于中等安全性. 功能性方面, OPE和ORE对数据库密态查询非常友好. 而SSE需要和借助树形索引将范围查询转换成多个等值查询, 变相地支持了范围查询, 集成进数据库需要做大量的适配开发. 因此对于密态范围查询来说, SSE的功能性要弱于OPE和ORE. 性能方面, 树形索引的SSE密文空间膨胀较大, 以平衡二叉树表示32位非负整数为例, 二叉树的层高是32层, 那么一个密文需要对应32个索引值, 即从二叉树根节点到密文所在的叶子节点路径上的所有节点都需要一个索引值, 空间复杂度为O(nlogA), 其中n为数据库大小, A为值域大小.
3.5 密态字符串查询字符串搜索包括多种类型: 等值搜索, 前缀搜索, 后缀搜索, 通配符搜索, 模糊搜索等. 字符串类型的等值搜索与其他数据类型的等值搜索实现方式相同, 基于密文的字符串等值搜索可以使用第3.3节介绍的方法实现. 前缀搜索和后缀搜索可以视为通配符搜索的特殊形式. 因此, 我们将密态字符串搜索归纳为两种类型: 密文字符串通配符搜索和密文字符串模糊搜索. 现有的密文通配符搜索方案和模糊搜索方案多为加密文档的检索场景设计. 在数据库场景下, 可将加密数据字段(column或field)作为加密文档, 因此这些方案也适用于密态数据库场景.
3.5.1 密文字符串通配符搜索字符串通配符通常有两种: “?”代表一个任意字符, “*”代表多个任意字符. 早期的密文字符串通配符搜索方案[55,56]多为枚举形式, 需要将关键词通配符的所有可能形式进行枚举, 因此效率低, 存储量大[57]. 为了解决这个问题, 文献[35,58]提出了基于SSE 和布隆过滤器(Bloom filter, BF)的特征提取方案. 布隆过滤器[59]由Bloom于1970年提出, 是一种基于哈希的概率数据结构, 可高效地将元素哈希值添加到集合中, 并测试集合是否包含某个元素.
2012年Suga等人[35]提出了以字符位置为特征的特征提取方案, 即将关键词里的每个字符与其在关键词中的位置结合起来作为特征. 例如, 字符串“cloud”, 可提取出5个特征{1||c, 2||l, 3||o, 4||u, 5||d}. 客户端为每个关键词构造一个布隆过滤器, 将该关键词的特征都添加到对应的布隆过滤器中. 利用 SSE将这个布隆过滤器作为索引, 与加密数据一同发送到服务端. 服务端建立倒排索引, 将每个关键词的布隆过滤器映射到它所属的文档. 搜索时, 客户端使用与上述相同的方法为包含通配符的搜索关键词提取特征. 例如“clo*”的特征集为{1||c, 2||l, 3||o}, “c?o?d”的特征集为{1||c, 3||o, 5||d}. 客户端为特征集生成布隆过滤器陷门, 并发送给服务端. 之后, 服务端扫描倒排索引, 找到包含陷门过滤器的关键词过滤器, 进而找到对应的加密数据. 不过我们可以看出, 该方案只适用于搜索关键词内字符位置可以确定的情况, 如上面提到的“clo*”形式的前缀搜索和“c?o?d”形式的位置固定的搜索关键词. 而对于后缀搜索“*oud”或“c*o*d”形式的字符位置不能确定的形式, 该方案则不适用.
2016年Hu等人[58] 在Suga等人[35]方案的基础上做了改进, 以支持更灵活的通配符形式. 该方案将字符的位置扩展为3种类型: (1)用正整数表示从前向后的位置; (2)用负整数表示从后向前的位置; (3)用0表示字符在关键词中存在. 这样, 关键词“cloud”的特征可扩展为{1||c, 2||l, 3||o, 4||u, 5||d, −5||c, −4||l, −3||o, −2||u, −1||d, 0||c, 0||l, 0||o, 0||u, 0||d}. 而后缀形式的搜索关键词“*oud”的特征可表示为{−3||o, −2||u, −1||d}, 字符位置不固定的搜索关键词“c*o*d”的特征可表示为{1||c, 0||o, −1||d}. 由此大大丰富了包含通配符的搜索关键词类型. 不过我们可以看出该方案的结果可能会有假阳数据, 如关键词cloud能够匹配“*cd*”的特征{0||c, 0||d}, 但并不是想要的结果. 因此客户端需要对搜索结果做后处理, 过滤掉假阳结果.
基于SSE和布隆过滤器的特征提取方案可以实现对密文的灵活通配符搜索. 然而, 安全性上不能达到SSE的IND-CKA[60]. 许多研究仍在探索安全性更高的方案. 如2020年Yang等人[61]提出基于同态加密的通配符搜索方案, 提高了安全性, 但降低了效率. 2021年Liu等人[62]基于布隆过滤器二叉树, 实现通配符多关键词搜索, 并改进服务端的倒排索引以增加安全性. 2023年Li等人[63]提出了基于内积(inner product)的通配符搜索方案, 支持所有类型的通配符搜索. 不过这些方案在增加安全性的同时, 也增大了存储容量和降低了搜索效率.
3.5.2 密态字符串模糊搜索字符串模糊搜索(fuzzy search)可将字符串进行模糊匹配, 从而可以找到与搜索关键词类似或相关的结果. 常见的明文模糊匹配算法包括编辑距离 (Levenshtein距离)、N-gram算法、Soundex算法等.
早期的基于密文的字符串模糊搜索方案主要思路是基于编辑距离为搜索关键词构造模糊关键词集. 2010年Li等人[64]提出首个密文上的模糊搜索方案, 利用编辑距离量化关键词的相似度, 并基于通配符或N-gram算法来构造模糊关键词集. 该方案的存储空间较大. 2011年Liu等人[65]提出了基于字典的模糊关键词集构造方案, 即模糊关键词集里的关键词必须是字典中有意义的单词, 从而大大减少了模糊关键词集的大小. 不过该方案的索引大小与加密文档的总关键词数量成线性关系, 存储空间依然较大. 2013年Wang等人[66]基于Li等人的方案[64]提出了结果可验证的密文模糊搜索方案, 并指出这两个方案的存储开销都为O(MN), M为模糊关键词集的大小, N为总关键词数.
之后提出了多个基于局部敏感哈希(locality sensitive hashing, LSH)的密文字符串模糊搜索方案. LSH可将对象映射到多个桶中, 相似度高的对象会被以较高的概率映射到相同的桶中, 而相似度低的对象会以较高的概率映射到不同的桶中. 2012年Kuzu等人[67]提出了基于LSH的密文字符串模糊搜索方案, 其利用LSH将相似度高的关键词映射到相同的桶中, 并在此基础上构建SSE安全索引. 为了提高系统安全性, 该方案将索引和字符串密文分别部署在两台不同的服务器上. 不过这导致查询需要两轮交互. 2014年Wang等人[68]基于LSH提出了首个多关键词密文字符串模糊查询方案. 该方案为每个文件构造一个布隆过滤器索引, 包含了文件中的每一个关键词. 为了支持多关键词模糊查询, 该方案将每一个关键词转换为一个bi-gram向量, 再利用LSH函数将关键词插入到布隆过滤器索引中. 搜索时以相同的方式将多个搜索关键词插入到布隆过滤器中生成陷门. 之后, 服务端将查询向量与索引向量做内积(inner product)操作, 量化查询关键词与每个文件的相关性完成搜索. 如果文件包含查询中的关键词, 则两个向量中的相应比特将为1, 因此内积将返回一个较大的值. 内积越大, 则文件包含越多的搜索关键词的概率越大. 因此, 内积结果可以很好地衡量匹配关键词的数量. 2017年Fu等人[69] 指出Wang等人[68]的方案仅对关键词中的一个字母错误有效, 而对其他常见的拼写错误则无效. 并且, 王的方案在排序过程中没有考虑关键词权重, 容易出现服务器乱序问题. 为了解决这些问题, Fu等人[69]提出了一个基于Wang等人[68]方案的高效多关键词模糊排序搜索方案. Fu等人开发了一种基于uni-gram的关键词转换方法, 提高准确性和处理拼写错误. 使用词根算法来查询具有相同根的关键词, 并考虑了关键词的权重. 2020年Zhong等人[70]指出Wang等人[68]和Fu等人[69]的方案有一个共同的缺点: 搜索时间O(n)与所有文档的个数n线性相关. Zhong等人[70]提出了一种动态多关键词模糊搜索方案, 利用平衡二叉树将所有的布隆过滤器索引聚合到一起, 使得搜索时间减少为O(rlogn), 其中r是包含查询关键词的文档数量.
3.6 密态算数运算半同态加密方案(partially homomorphic encryption, PHE)支持基于密文做指定的算数运算, 产生的密文经解密之后得到的结果, 与对明文数据进行相同算数运算得到的结果相同. 因此, PHE 可用于执行安全的数据库聚集操作, 如加和、平均值、最大值、最小值等.
按照底层加密算法类型的不同, PHE可分为两大类: (1)基于非对称加密算法的PHE. 1985年提出的ElGamal方案[71]和1999年提出的Paillier方案[72] 是两个是最典型的PHE方案, 它们都是非对称的概率加密方案, 都为语义安全(IND-CPA). ElGamal支持密文的同态乘除法运算, Paillier支持密文同态加减法运算、密文与明文的加减法运算、密文与明文的乘法运算. 根据2022年的一则研究[73], ElGamal的密文同态乘法的平均运算效率比明文慢约
此外, 还有一些研究对已有的PHE方案做性能优化, 以提高其运算效率. 2023年Tawose等人[76]提出了基于基数(radix-based)的并发缓存优化方案, 用以加速云外包数据库的同态运算速度. Tawose等人观察到, 现有PHE算法的加密操作开销要远大于算数运算操作的开销. 因此, 其设计的缓存优化方案在不降低原始同态加密算法安全性的前提下, 通过并发缓存选定基数的密文, 显著地减少在批量或增量加密的过程中的加密操作次数. 通过6种不同的工作负载的实验, Tawose等人称他们所提出的并发缓存方案可以将 Paillier和Symmetria等最先进的PHE方案的运算速度提升多达5个数量级.
3.7 通用加密方案上面介绍的加密方案都只能支持部分密态查询, 还有两种通用的加密方案: 全同态加密(fully homomorphic encryption, FHE)和混淆电路(garbled circuit, GC). 理论上, 全同态加密和混淆电路可以支持任何密文计算, 从而支持任何密态数据库运算.
3.7.1 全同态加密(FHE)全同态加密支持基于密文做任意类型运算, 产生的密文经解密之后得到的结果, 与对明文数据进行相同算数运算得到的结果相同. 全同态加密的概念最早可以追溯到1978年由Rivest等人[77]提出的隐私同态(privacy homomorphisms)概念, 即对密文进行计算, 间接地对明文进行操作的构想, 之后被扩展为全同态加密. 全同态加密概念一经提出, 就受到了整个密码学界的关注, 被称为现代密码学的圣杯. 但经历了30多年的研究和探索, 直到2009年才由当时读博士的Gentry[78]提出了第1个理论上可行的全同态方案. 之后, 在Gentry方案原理的启发下, 各类全同态方案[79−86]如雨后春笋搬涌现. 整体的发展脉络可归纳为在保障安全性的前提下, 改进全同态加密方案的性能, 使之能够真正地实际运用.
尽管全同态加密经历了十几年的蓬勃发展, 但和传统加密算法相比, 其时间开销和存储开销依然极高. 最近的一个研究[73]对两个经典的FHE开源库SEAL和HElib进行了性能测试. 测试结果表明, FHE加法的效率比明文计算慢10万到100万倍, 而乘法比明文慢
混淆电路最早由姚期智先生[87,88]提出, 用于解决百万富翁类的多方安全计算问题. 理论上, 混淆电路可以支持任何类型的密态运算, 并且是语义安全的(IND-CPA). 但为了保障安全性, 混淆电路通常不可重复使用(这里暂不考虑性能上还不具有可实践性的可重复执行方案[89−92]), 执行过一次之后, 需要重构该电路. 因此, 混淆电路方案需要大量的计算、带宽和交互, 会导致很高性能开销和延迟. 由于其较低其性能, 仅有少量的研究基于混淆电路实现全密态数据库, 详见第3.8.3节和第3.8.4节.
3.8 基于软件加密算法的全密态数据库系统表5总结了基于软件加密算法的全密态数据库, 它们的安全模型都是针对半诚实型敌手(被动型敌手). 其中CryptDB[93−95], Monomi[96], BlindSeer[97]和Arx[98]是学术研究的原型系统. MongoDB的Queryable Encryption[99,100]是最近工业界的产品.
| 表 5 基于软件加密算法的全密态数据库概览 |
3.8.1 CryptDB
2011年Popa等人[93]提出了CryptDB, 并在后续几年对其做了一系列优化工作[43,94,95,101]. CryptDB是第一个功能较完整且实用的全密态数据库系统. CryptDB支持密文上的等值查询、范围查询、LIKE查询、连接、聚集、GROUP BY、ORDER BY等操作. 在架构上, CryptDB基于现有数据库MySQL或PostgreSQL实现. 通过在客户端与服务端增加数据库代理(database proxy)、在服务端实现用户定义函数(UDFs)的方式, 在无任何修改的现有数据库上, 实现了基于密文的各种搜索操作. 客户端代理负责识别查询SQL中的加密列并改写与之相关的查询条件, 使得加密数据上的操作对客户端应用程序透明. 服务端增加的用户自定义函数负责完成基于密文的各种操作, 结合客户端代理对查询SQL的改写, 实现了无需修改现有数据库即可基于密文的各种查询操作. 为了支持不同的密文操作, CryptDB采用了多种加密方案, 并创新地设计了一种“洋葱加密模型”. 具体地, CryptDB将一列明文存储成多列密文, 不同的密文列支持不同的密文操作. 数字类型的明文列, 有3个对应的密文列, 分别是DET密文列、OPE密文列和PHE密文列, 分别对应数值的等值查询、范围查询和聚合操作. 字符串类型的明文列, 也有3个对应的密文列, 分别是DET密文列、OPE密文列和SEARCH密文列, 对应字符串的等值查询、范围查询和LIKE操作. SEARCH是CryptDB设计的一个基于SSE的字符串通配符加密方案. 为了进一步增加密文列的安全性, CryptDB设计的“洋葱加密模型”将每一列密文都做多次加密, 像洋葱一样将密文一层一层包裹起来. 最内层(最先加密的)是安全性较低的密文, 如DET密文、OPE密文, 最外侧是安全性较高的密文, 如RND密文. 当将一条新的数据插入时, 客户端代理将明文用不同的加密算法加密成多列, 每一列加密多次, 发送给服务端存储. 由于最外层密文是RND密文, 不支持任何密态查询. 因此在查询时, 客户端代理会先发送一个update SQL给服务端, 将对应的密文列解密到能够支持该查询操作的密文, 比如DET密文. 解密完成后, 再将改写的查询语句发送给服务端查询. 为了提高查询效率, 在查询后并不会马上把解密的列加密回RND密文, 而是等到对该列的查询不频繁时再加密回去.
当系统稳定运行后, CrypDB的查询效率是比较高的, 因为对于最频繁的等值查询和范围查询, DET密文和OPE密文都是比较高效. 相比于明文的phpBB测试, CryptDB吞吐量上降低了14.5%; 相比于明文的TPC-C测试, CryptDB在吞吐量上降低了26%[93]. 此外, CryptDB虽然将一个明文列存储为多个密文列, 但相比于其他加密方案(如SSE或FHE), 其存储开销还是相对较小的.
但CryptDB的安全性是饱受争议的. 首先, 查询时最外层的RND密文会被解密成安全性较低的DET或OPE密文, 导致被查询列的密文安全性会从RND的安全性退化为DET或OPE的安全性, 并且解密密钥也会被服务端获知, 这大大降低了洋葱加密模型的意义. 其次, DET和OPE的安全性是较弱的, 2015年Naveed等人[5]通过推理攻击, 破解了存储在CryptDB内的美国公开医疗数据中60%的医院超过60%的患者DET加密记录(例如, 性别、种族和死亡风险), 以及95%的医院中超过80%的患者记录的某些OPE加密数据(例如, 年龄和疾病严重程度). 从这之后, CryptDB的安全性就争议不断, 学术界也开始纷纷研究用于替代DET和OPE的更安全且实用的加密方案.
3.8.2 Monomi2013年Tu等人[96]提出了第1个分析型(OLAP)的全密态数据库Monomi. 该数据库基于CryptDB, 通过3方面的优化, 使之适用于分析型任务: (1)将复杂查询拆分成服务端与客户端共同完成. 例如在密文上的聚集操作. CryptDB在服务端通过计算PHE算法Paillier的密文完成, 但Tu等人发现在聚集的数据量不大的情况下, 客户端解密Paillier计算结果的开销要远大于客户端自己解密OPE密文再做聚集的开销. 因此, Monomi会根据查询条件将复杂查询的执行拆分到服务端和客户端, 减少查询的整体时间开销; (2)引入了多种优化技术改进特定类型的分析型查询(但不适用于所有类型的查询), 这些优化技术包括每行预计算、节省空间的加密、分组同态加法和预过滤等. Tu等人观察到分析型数据库的瓶颈在于I/O(如从磁盘读取数据), 而密态数据库导致密文数据膨胀, 会进一步加剧数据库系统的I/O压力. 通过前述的这些优化技术可以大大提高分析型查询的I/O效率; (3) Tu等人设计了一个用于优化服务器物理数据布局的设计器, 以及一个用于决定如何在客户端和服务器之间划分查询执行的规划器. 通过以上3方面的优化, Monimi在TPC-H测试上的平均执行时间, 是未加密数据执行时间的1.24倍.
尽管Monimi继承了CryptDB的诸多优点, 如支持大多数的数据库操作、密文操作效率高等, 并针对特定的分析型任务做了性能优化. 但Monimi也同时继承了CryptDB在安全性上的弱势, DET和OPE密文暴露的明文重复频率和分布信息, 使得Monomi的安全性整体上是比较低的.
3.8.3 BlindSeer2014年Pappas等人[97]提出了一个基于布隆过滤器搜索树(BF search tree)和混淆电路(GC)的全密态数据库BlindSeer, 支持大规模数据上的等值查询、范围查询和布尔查询. BF search tree是一个N叉树(Pappas等人采用的是10叉树), 是BlindSeer在服务端构造的密态索引, 每个加密表仅对应一个这样的索引. 树的叶子节点对应一条加密数据记录, 非叶子节点对应一个布隆过滤器, 包含其下面所有记录的所有属性值. 例如, 某个表有两个属性A和B, 某一记录对应的属性值为a和b. 那么该条记录加密后对应BF search tree上的一个叶子节点, 而A:a和B:b会当作两个关键词, 加入该叶子节点的所有祖先节点的布隆过滤器内. 这样给定任意的等值查询条件, 就能通过从上到下遍历BF search tree来找到所有匹配的叶子节点(记录). 不过由于索引树内的记录不是按某个属性排序的, 对于范围查询, 需要多次遍历索引树, 逐一查找范围内每一个值对应的叶子节点. 为了保障安全性, BlindSeer使用混淆电路来遍历索引树. 每次遍历, 客户端构造一个对应的混淆电路Q发送到服务端, 混淆电路Q能够判断布隆过滤器节点是否包含查询条件内的属性值. 服务端收到混淆电路Q之后, 从索引树的根节点开始, 从上到下逐层、逐节点执行该混淆电路Q, 直到找到对应的叶子节点为止. 由于每个布隆过滤器节点都包含该表所有的属性值的关键词, 因此布隆过滤器索引树可以方便地支持该表的多属性布尔查询.
BlindSeer具有很好的安全性, 不仅保护了敏感数据的机密性, 而且通过混淆电路保护了查询模式(query pattern). 但BF search tree索引结构比较适合静态数据, 对动态更新(插入、更新、删除)并不友好. 此外, BlindSeer支持的数据库操作比较有限, 仅支持等值、范围和布尔查询, 不能够支持连接(join)、聚集(aggregate)、投影(projection)、TopK查询等操作. 并且对于范围查询, 需要多次遍历搜索树, 每一次遍历都需要客户端与服务端交互, 有极大的时间延迟. 因此BlindSeer的方案不适用于通用型的全密态数据库.
3.8.4 Arx2016年Poddar等人[98]提出Arx, 一个仅基于语义安全加密方案的全密态数据库. 架构上, Arx基于MongoDB实现, 并从CryptDB的架构设计中吸取经验, 不对现有数据库做任何修改, 而是增加了客户端代理和服务端代理, 所有的密态操作都通过这两个增加的代理完成. 客户端代理包含数据库计划器(planner)和查询重写器(query rewriter), 负责解析query并改写与密文相关的查询语句. 服务端代理负责构建Arx设计的密态索引, 传递给MongoDB存储, 并在查找时执行相关的密态查询逻辑. Arx设计了两种类型的密态索引, 分别是支持等值密态查询的ArxEq和支持密态范围查询的ArxRange.
ArxEq基于SSE加密方案. 插入数据时, 客户端将明文加密成随机密文, 同时使用伪随机函数(PRF)生成密文索引值, 一并发送给服务端存储. 由于PRF是确定性的, 相同明文的密文索引值也相同. 为了避免泄漏明文的重复频率, ArxEq在服务端为每一个相同的明文维护一个计数器(counter). 当服务端收到确定性的密文索引值时, 找到对应的计数器, 并用计数器当前值将密文索引值二次加密, 再存储到ArxEq索引结构中. 这样对于每一个相同的明文, 其存储在服务端的最终密文索引值都互不相同; 查询时, 客户端使用PRF为明文生成与上述相同的确定性密文索引值, 即为查询token. 服务端收到该查询token后, 找到对应的计数器, 并使用PRF将一个token二次加密成多个密态索引值, 查找到对应的所有文档(document)返回给客户端. 由此可见, SSE与计数器的结合是ArxEq能够隐藏等值频率信息、达到语义安全的关键设计.
ArxRange基于混淆电路和二叉树索引构建, 服务端可以自行遍历二叉树索引. 每一个加密的属性, 对应一个加密二叉树索引. 其中每个叶子节点关联一个文档ID, 每个非叶子节点是一个混淆电路(GC), 其内编码了密文索引值、密钥e (不同于服务端存储的随机密文的密钥), 以及比较函数. 范围查询时, 客户端代理使用密钥e将查询条件中的明文加密成随机密文, 服务端收到该随机密文后, 从二叉索引树的根节点开始, 对该密文执行节点内的混淆电路, 根据得到大于或小于的执行结果, 继续执行对应的下层节点的混淆电路, 直到找到对应的叶子节点(或找不到对应的结果), 完成遍历. 混淆电路的安全性保证了服务端只能获知比较的结果, 而对查询条件中的明文和二叉树节点中编码的索引值一无所知. 但这里存在一个挑战, 混淆电路的安全性基于其只能执行一次, 如果执行多次就泄漏除结果外的其他信息. 因此二叉搜索树在遍历一次之后, 需要与客户端交互, 修复(重新构建)执行过的混淆电路. 修复的个数为O(logn), n为该加密属性的总数据量.
Arx的安全性较高, 得利于其仅使用语义安全的加密算法. 但Arx支持的数据库操作较少, 只能做等值查询、范围查询相关的数据库操作, 不能做连接、字符串模糊查询等复杂的数据库操作, 这可能是Arx基于非关系型数据库MongoDB实现的原因之一. 此外, 出于安全性考虑, 混淆电路通常不能重复执行(这里没考虑性能还不具有可实践性的可重复执行方案). 因此ArxRange的二叉树索引节点上的混淆电路是一次性的, 每次遍历之后都需要修复执行过的混淆电路, 导致大量的客户端与服务端之间的交互, 产生了很大延迟. 这也导致遍历二叉树需要串型执行, 无法并发处理. 综合来看, Arx的设计方案虽然安全性高, 但性能低, 功能上也不适用于通用的全密态数据库.
3.8.5 MongoDBMongoDB于2022年6月上线了Queryable encryption功能[99,100], 是当时工业界唯一一款只使用纯软件加密算法的全密态数据库. Queryable encryption使用SSE实现密文等值查询, 并会在后面的版本发布基于SSE的范围查询.
MongoDB的密文等值查询主要方法如下: 当插入一个包含敏感字段的文档(document)时, 客户端使用随机加密算法加密明文、使用伪随机函数(PRF)生成加密索引值. 由于伪随机函数是确定性的, 相同的明文会生成相同的加密索引值. 服务端收到包含密文的文档和加密索引值后, 为了隐藏相同加密索引值的重复信息, 为每个相同的加密索引值都分配了一个序号(count), 并使用伪随机函数对加密索引值和序号做二次加密. 二次加密后的加密索引值都是互不相同的(即使明文相同). 然后服务端在该文档内增加一个名为__safeContent__的集合类型字段保存该文档的所有加密索引值, 这个__safeContent__集合就是Queryable encryption的加密索引. 可以看出该加密索引没有集中存储在服务端的某个数据结构内(如B+树等), 而是分布存储在每一个包含敏感字段的文档内. 查找时, 客户端使用伪随机函数生成加密索引值, 该值就是查询token (陷门). 服务端收到查询token后, 根据为其分配的所有序号, 将该token二次加密成多个加密索引值, 并查找那些__safeContent__字段包含任意一个加密索引值的文档, 返回给客户端. 从上述方案我们可以看出, Queryable encryption的加密索引值都互不相同, 如果伪随机函数的随机性足够好, 那么存储在服务端的加密索引值近似于随机密文, 但客户端发给服务端的加密索引值(查询token)是确定性的, 因此该等值查询方案的具有中等安全性, 为典型的SSE方案安全性IND-CKA. 性能依赖于服务端存储的文档数量n、加密索引值编号的个数m, 以及返回的结果大小R, 因此时间复杂度为O(n×m+R).
MongoDB的密文范围查询原理和第3.4.4节中Demertzis等人[34]的基于SSE和树形索引的一维范围查询方案非常相似, MongoDB采用了Logarithmic-BRC形式的范围覆盖方案. 不同的地方在于, MongoDB的范围索引没有使用字典结构来存储索引密文, 而是复用了其密态等值索引的实现, 将索引密文存储在每一个文档的__safeContent__集合内. 并且为了隐藏相同索引密文的频率, MongoDB的范围索引密文也同等值索引密文一样维护了每个相同值的序号, 使用该序号为索引密文做二次加密, 使得所有的所有密文都是不相同的. 不过, 同时也增加维护序号的开销.
相比基于DET和OPE的CryptDB, MongoDB的安全性大大增加了, 除了访问模式和查询token之外, 基本没有向服务端暴露明文的其他信息. 但SSE加密方案在密文空间上的膨胀比DET和OPE算法大得多. 例如对于32位的整数明文, 使用SHA256作为伪随机函数对其做等值和范围密文索引, 那么会产生一个随机密文、一个等值查询索引、32个范围查询索引密文(32层的树形索引), 以及序号等元数据信息, 总的密文空间会是明文的200多倍. 密文的空间膨胀会增加数据的I/O开销和计算开销, 此外维护相同明文的序号, 也会对性能有较大影响.
4 基于可信硬件TEE的全密态数据库关键技术基于可信硬件TEE的全密态数据库依赖可信执行环境来实现密文上的数据库操作. 可信执行环境是一种基于可信硬件的安全技术, 为安全计算提供机密性和完整性保护, 使得敏感数据的计算可以被拆分到TEE中执行, 其余非敏感数据的计算在传统的不受信任的富执行环境(rich execution environments, REE)中运行, 避免攻击者的恶意操作或云主机管理员的窥探. 代表性的TEE有Intel SGX[102,103]、AMD SEV[104]、ARM TrustZone[105]等. 目前, Intel SGX是全密态数据库中使用最广泛的TEE, 本文后面主要以SGX为主介绍基于TEE的全密态数据库.
TEE供一个称为飞地(enclave)的可信代码和数据区域, 并向应用进程、操作系统和系统管理员隐藏了飞地内的运算和状态, 以在不受信任的云主机进程中进行可信运算. TEE实现了3个主要功能[106]: (1)隔离(isolation): 保护飞地内的代码和数据不会被任何外部进程读取或修改; (2)密封(sealing): 发送到飞地外的数据都被加密和验证; (3)认证(attestation): 使用专用的签名密钥和指令生成不可伪造的认证结果, 保障飞地内的代码、数据, 以及在飞地内部执行的计算输出都是可信的.
以Intel SGX为例, 飞地是进程中一个独立的虚拟地址空间, 在这个空间中, 代码和数据存储在被保护的内存页面中, 称为飞地页面缓存(enclave page caches, EPC). EPC中的数据由内存加密引擎(memory encryption engine, MEE)加密, 并且在EPC中始终保持密文状态, 只有被加载到CPU缓存中的数据才能够被解密. 需要通过加载指定的SGX库来初始化飞地, 之后服务端的应用程序需要使用指定的SGX库函数ECall和OCall与飞地内的代码和数据进行交互. 此外, Intel SGX提供远程认证(attestation), 允许客户端验证飞地的真实性以及远程主机上加载的代码和数据的完整性.
4.1 TEE在全密态数据上的应用与挑战TEE的可信特点, 使之可以被视为客户端在服务端的延伸. 借助认证(attestation)协议, 客户端可以将解密密钥安全地传递给TEE. 这样, REE内不受信任的云数据库可以借助TEE将密文数据解密成明文, 并完成指定的运算(如比较大小、求和等), 获取运算结果来完成对应的数据库操作. 解密后的明文始终在enclave内, 并在其内完成运算, TEE的安全性保障其不会被窥探和篡改. 根据功能需要, 运算结果可以明文形式返回给REE, 例如服务端需要比较大小的结果来构建密文的B树索引; 运算结果也可以在enclave内加密后再返回给REE, 例如加密列的求和结果. 由此可见, 基于TEE的全密态数据库是借助enclave在明文上完成各种运算, 因此理论上可以支持任何数据库操作, 功能性上大大优于基于加密算法的全密态数据库. 近些年越来越多的全密态数据库选择基于TEE实现. 不过将TEE应用到数据库中存在着如下的一些挑战.
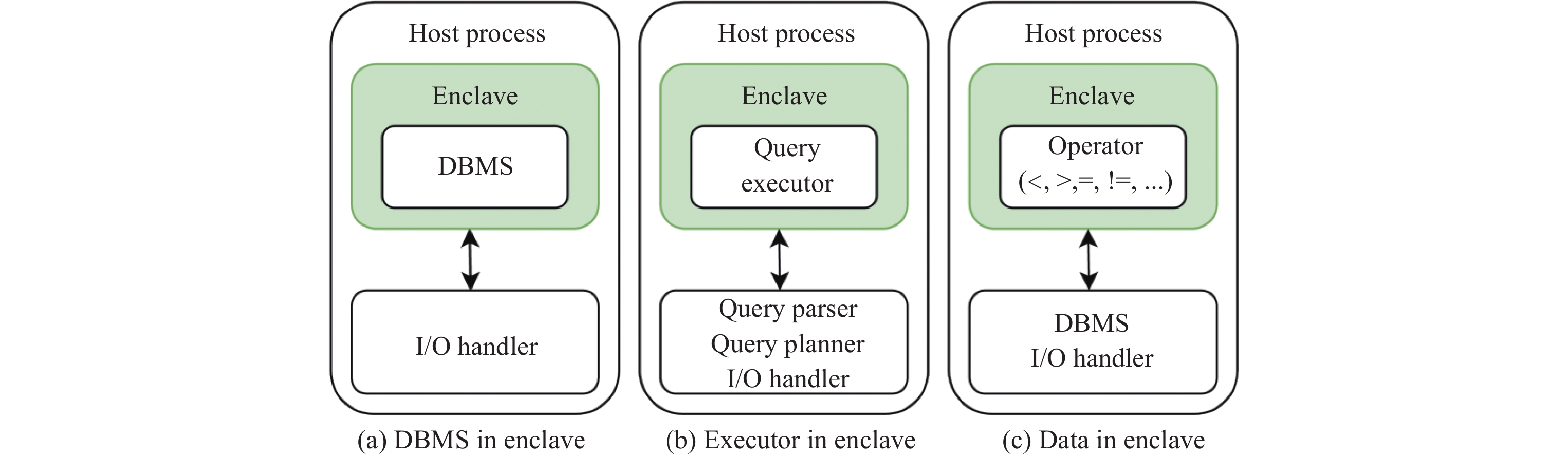
4.1.1 挑战1: 数据库功能在TEE与REE之间的拆分将TEE应用到全密态数据库的第1个挑战是确定如何在受信任的TEE和不受信任的REE之间划分查询的处理, 即数据库的哪些部分在TEE中执行, 哪些部分在REE中执行. 如图4所示, 按照放入TEE enclave的数据库模块由大到小, 可以有3种设计模式[106]: (1)整个数据库放入TEE. 此模式将整个数据库都放入TEE中执行, 包括查询解析器、规划器、执行器等数据库的功能模块, 以及数据库中存储的数据, 相当于以内存数据库的形式运行. EnclaveDB[107]选择此模式, 所有加密数据都加载到TEE中以明文形式运算. 由于TEE中的代码不能直接访问I/O, 需要通过REE中的I/O handler完成I/O操作. 当数据库的运行内存大于TEE内存容量时, 一部分数据需要交换到磁盘上, 会出现大量的TEE和REE之间的I/O交互, 导致性能急剧下降. 此外, 这种模式可能会带来安全性隐患. 由于整个数据库都运行在可信的TEE内, 一旦数据库或操作系统内核存在安全漏洞, 被黑客攻击(如SQL注入攻击、提权攻击), 那么相关的程序执行也可能会被认为是可信的, 从而造成安全事故. (2)部分执行器放入TEE. 该模式将处理密文数据所需的部分DBMS模块放在TEE中, 其他部分留在REE中. TrustedDB[108,109]和CipherBase[110,111]选择此模式, 将执行器的部分功能放在TEE内, 部分留在REE中. (3)算子放入TEE. 此模式仅将算子(operator)放入TEE内, 如比较、加减乘除等. 加密的数据从REE传入TEE供算子运算, 而其他的数据库的功能模块都在REE中执行. 加密的数据在TEE内被解密成明文, 并基于明文执行指定的运算(如比较大小), 计算结果返回给REE中的DBMS功能模块. 从可信计算基(trusted computing base, TCB)的角度来看, 仅将算子放入TEE时, TCB最小, 系统的攻击面也最小, 更容易实施安全控制. 目前大多数全密态数据库选择此模式, 如Always Encrypted[2], Enclage[3], GaussDB[4], StealthDB[106]等.
|
图 4 基于TEE的全密态数据库的3种设计模式 |
4.1.2 挑战2: 数据的加密粒度
第2个挑战是确定数据的加密粒度. 加密粒度越大, 泄露的信息越少, 存储开销越小, 利于批量处理. 但集成的成本高, 读写数据不够灵活. 即使只读取一个基础数据项, 也需要将整个粒度的加密数据加载到TEE enclave中. 加密粒度越小, 数据处理越灵活(利于非批量处理), 集成成本越低. 但泄露的信息越多, 存储成本也越高. 大多数全密态数据库都对基本数据对象进行加密, 例如元组(tuple)、单元(cell)、索引值等. Enclage[3]选择对整个索引页进行加密以达到更好的安全性.
4.1.3 挑战3: 有限的enclave内存空间2015年, Intel推出第1代SGX, 其enclave内存在启动加载时静态分配, 大小只有固定的128 MB[112], 其中的96 MB用于enclave页面缓存(EPC), 保存被保护的代码和数据. 之后推出的CPU将enclave内存大小扩展到了256 MB[3]. 虽然Linux上可以通过系统分页将enclave大小设置在128 MB以上, 但Intel官方出于性能考虑仍建议将其限制在128 MB内. 这样的内存限制对于现代数据库无疑是非常小的, 因此对于基于第1代SGX的全密态数据库, 有限的enclave内存大小是一项挑战.
2021年, 第2代SGX引入了enclave动态内存管理(EDMM), 可以动态分配enclave内存, 大大增加了enclave内存容量. 目前单CPU的enclave内存可支持到512 GB[113]. 如果通过Intel multi-socket系统支持多CPU, 可将enclave内存扩大到1 TB (https://www.intel.com/content/www/us/en/architecture-and-technology/software-guard-extensions-processors.html). 这样大大缓解了第1代SGX enclave内存不足的问题.
4.1.4 挑战4: TEE与REE交互的巨大开销TEE与REE之间的交互开销成本巨大. 以Intel SGX为例, 当REE调用TEE时, REE内的主机程序(host process)只能通过ECall函数调用enclave内的程序或将数据传入enclave. 而当TEE调用REE时, 由于enclave运行在用户态, 无法直接执行系统调用, 需要通过OCall调用到REE来执行. ECall和OCall的开销非常大, 可能需要
表6显示了基于TEE的全密态数据库的比较. 这些数据库都是关系型数据库, 并且都使用B-tree作为索引结构. StealthDB[106], 和Enclage[3]对索引节点中的密文进行了重加密, 避免B-tree索引泄露密文的顺序, 这样可以避免索引密文的安全性降低到OPE的安全性级别. GaussDB[4]通过名为secGear[115]的自主研发的中间件支持Intel SGX和Arm TrustZone两种TEE. 加密粒度列中的对象可以是tuple, cell value, 索引key等数据.
| 表 6 基于TEE的全密态数据库 |
2011年Bajaj和Sion提出了TrustedDB[108,109], 基于可信硬件IBM 4764的全密态数据库(此时还没有SGX等目前流行的可信硬件). IBM 4764拥有类似Intel SGX的安全协处理器(secure coprocessor, SCPU), SCPU拥有类似enclave的空间十分有限的被保护存储区域.TrustedDB将数据分为两类: 未加密的公开属性(public attributes)和加密的隐私属性(private attributes). 对应地, TrustedDB在架构上也将一些数据库模块拆分成两部分, 一部分在不受信任的REE中处理公开属性数据, 另一部分在受信任的TEE (SCPU)内处理私有属性数据, 这些模块包括解析器、优化器、执行器等. 查询的执行可以分成如下步骤.
(1) 客户端定义数据库模式(schema), 敏感属性使用SENSITIVE关键词进行标记. 通过该关键词, 客户端透明地加解密隐私属性的敏感数据.
(2) 查询时, 客户端将查询(query)加密, 通过标准SQL接口发送给云服务端. 加密密钥是SCPU的公钥(这里与Intel SGX不同, SGX的加解密密钥是客户端拥有并授权给TEE).
(3) 云服务端收到加密的查询请求后, 转发给SCPU内的请求处理模块(request handler).
(4) 请求处理模块解密查询, 发送给查询解析器. 查询被解析, 并拆分成一组查询计划(plans). 每个查询计划都是通过将原始客户端查询重写为一组子查询来构建的, 并且根据其目标数据集分类, 计划中的每个子查询被标记为public或private.
(5) 查询优化器评估每个查询计划的执行代价, 选择代价最小的查询计划, 发送给查询调度器(dispatcher).
(6) 查询调度器将标记为public的子查询发送到REE环境的数据库引擎执行, 将标记为private的子查询发送到SCPU内的数据库引擎执行, 并处理它们的依赖关系.
(7) 最终结果经过查询调度器组装、加密、签名, 然后发送给客户端.
TrustedDB是基于可信硬件的全密态数据库的先驱, 其很多设计现在看来仍然非常先进. 但受限于当时的可信硬件技术, 以及之后以Intel SGX为代表的TEE快速发展, TrustedDB并没有在工业界大范围推广.
2013年微软的Arasu等人[110,111]提出CipherBase, 基于定制化硬件FPGA的Microsoft SQL Server扩展, 支持几乎所有的SQL操作. CipherBase借鉴了TrustedDB的设计, 将可信硬件和云服务器组合在一起. CipherBase将云服务器上的不可信环境称为UM (untrusted module), 可信环境称为TM (trusted module), 类似于现在的REE和TEE. TM基于定制化硬件FPGA, 一个UM可以有多个TM, 对应多个FPGA. 每个TM都有烧制在硬件上的独有密钥, 使用该密钥, TM可以将应用程序的密钥加密并存储在UM内. 由于可信硬件的算力和内存有限, 不可信环境的算力更强、内存更大, CipherBase出于性能考虑没有像TrustedDB那样将与密文相关的所有运算都放在TM内执行, 而是仅将解密和基于明文的操作放在TM内执行, 其他操作放在UM内执行. 例如, 对于Hash Join操作, TM负责计算hash和检查是否相等, 其他逻辑则由UM完成. 不过, Vinayagamurthy等人[106]指出基于FPGA会有安全隐患, 需要进行大量研究才能将其用作云数据库的可信硬件.
2018年Priebe等人[107]提出EnclaveDB, 基于Intel SGX的内存数据库. 其工作模式是将所有的敏感数据(数据库表、索引和其他元数据)都放入到enclave内, 相当于将整个DBMS都放入到了enclave内执行. 此外, EnclaveDB客户端将包含敏感数据的查询编译成本地代码(native code), 再经过签名和加密后, 部署到云服务端的enclave上. 这样查询解析器、编译器和优化器就可以都放在enclave内执行, 减少了攻击者可以利用的攻击点. EnclaveDB客户端通过与enclave建立安全通道并发送带有加密参数的请求来执行预编译查询. enclave对请求进行验证、解密参数、执行预编译的查询、加密查询结果, 并将结果发送回客户端. EnclaveDB作为内存数据库, 对于数据总量小于enclave内存容量的数据库比较高效. 但当数据量大于enclave内存容量时, 一部分数据需要交换到磁盘上, 会出现大量的TEE和REE之间的I/O交互, 导致性能急剧下降.
2019年Vinayagamurthy等人[106]提出StealthDB, 基于Intel SGX的全密态数据库. StealthDB选择仅将加密数据和对应的运算传入enclave执行. 优点是对现有数据库的改动较小, 与磁盘和网络通讯的模块都无需改动, 仅需要修改敏感数据相关的运算符的执行方式即可. 并且enclave内的代码和数据量非常小, 容易实现不经意传输, 保护访问模式(详见第6节). StealthDB借助enclave为密文构建了B-tree索引. 不过文中的实验显示, 由于ECall和Ocall昂贵的开销, 相比于明文B-tree索引, 利用enclave逐个执行比较操作的密文B-tree索引要慢100倍以上. 为了更好的安全性, StealthDB为每个密文索引键做了二次加密, 否则B-tree索引会暴露密文的顺序, 使得其安全性降低为OPE的水平; 另外, 索引页也被加密后再存储到磁盘上. StealthDB的原型实现基于PostgreSQL, 支持完整的TPC-C测试, 与明文数据量为2 GB的未修改PostgreSQL相比, StealthDB在密文上执行的平均吞吐量下降了30%.
2020年微软的Antonopoulos 等人[2]提出了SQL Server第2版Always Encrypted (AEv2). 第1版Always Encrypted (AEv1) 随SQL Server 2016发布, 仅支持确定性加密列上的等值查询. AEv2随SQL Server 2019发布, 基于微软的虚拟化技术Windows virtualization-based security (VBS) enclaves (https://learn.microsoft.com/en-us/windows-hardware/design/device-experiences/oem-vbs), 之后改为使用Intel SGX. 与StealthDB相似, AEv2也仅将加密数据和对应的操作发送到enclave内解密执行, 并为密文构建了B-Tree索引. 不过AEv2没有为B-Tree的索引键做二次加密, 因此暴露了密文的顺序. 此外, AEv2仍然保留了AEv1的确定性加密(可能是处于向后兼容考虑), 这也会暴露确定性密文的频率.
2021年阿里的Sun等人[3]提出了基于Intel SGX的enclave原生数据库存储引擎Enclage (enclave+storage). 与StealthDB和AEv2类似, Enclage也借助enclave为密文构建B-Tree索引. 不同的是, enclave的加密粒度不是加密列的数据项(item), 而是整个内存页. 虽然这样大大增加了集成的难度, 但提高了安全性、降低了存储开销, 也提高了数据批处理的效率.
5 软硬融合的全密态数据库软硬融合的全密态数据库融合了软件加密算法和可信硬件TEE双方的优点, 部分查询操作利用加密算法和REE加密索引在REE下执行, 部分操作利用可信硬件和TEE加密索引在TEE下执行, 显著地降低REE和TEE之间的交互开销. REE加密索引和TEE加密索引都是基于密文或加密索引值构建出来的索引, 他们的主要区别在于, REE 加密索引的构建和查询依赖于加密算法, 运行在具有更多计算资源的REE中; 而TEE加密索引则依赖于TEE enclave将密文解密成明文, 并在明文上进行计算. 软硬融合架构的主要挑战在于如何正确地选择和分配REE与TEE中的查询操作, 以降低执行开销.
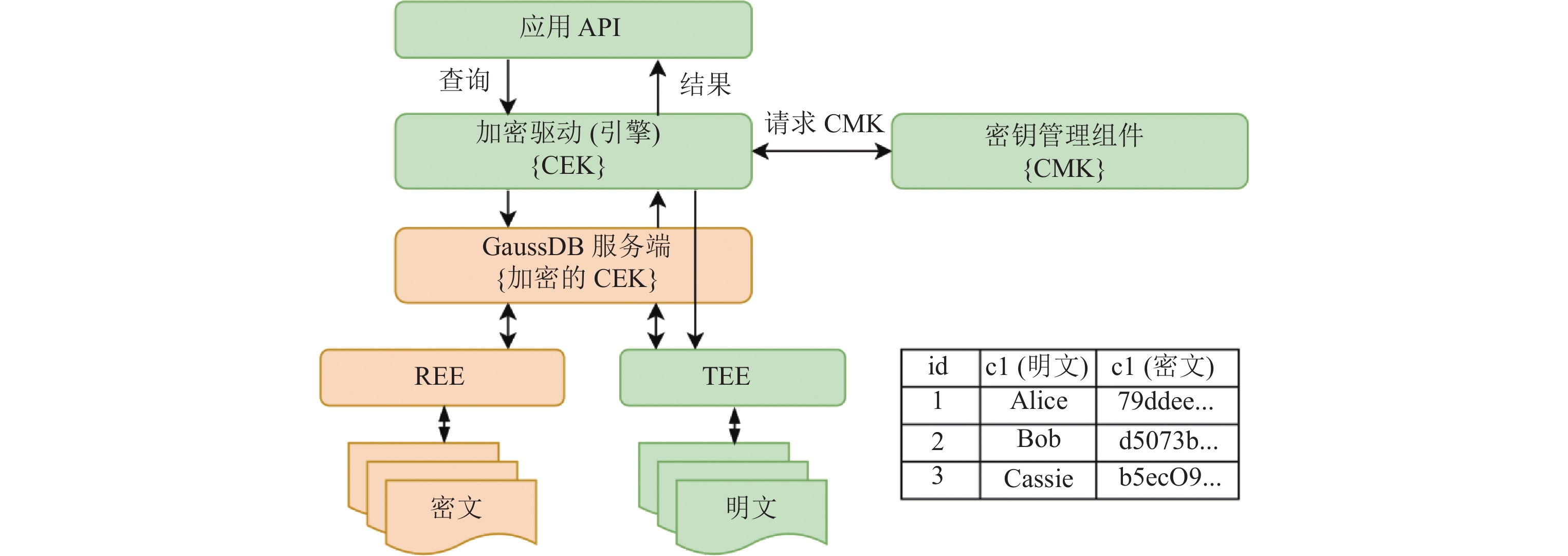
GaussDB[4]是软硬融合的全密态数据库的典型代表, 其架构如图5 所示. GaussDB提供了两个执行模式, 基于REE的软件执行模式和基于TEE的可信硬件执行模式. GaussDB会根据查询的功能划分和代价估计, 自适应地选择使用哪个模式执行. 敏感数据以列为单位加密存储在服务端, 而列加密密钥也被加密后存储在服务端.
|
图 5 GaussDB软硬融合全密态架构 |
GaussDB的密钥体系分为3层.
(1) 列加密密钥(column encryption key, CEK)
第1层是列加密密钥CEK. CEK通过随机初始向量对列属性的不同数据进行随机加密, 保证了各个属性之间的加密隔离. 如果一个CEK泄露, 则只有与之相关联的属性会受到影响.
(2) 用户主密钥(client master key, CMK)
第2层是用户主密钥CMK. 不同的用户使用自己唯一的CMK来加密自己的CEK. CMK永远不会离开用户的可信环境. 这样, 即使自己的数据被他人恶意访问, 也无法破译数据所有者加密的密文数据.
(3) 设备密钥(device key, DK)
第3层是设备密钥DK. 不同的DK可用于保护不同的CMK, 实现用户侧客户端设备之间的加密隔离, 进一步提升整体的安全性.
软件模式下, GaussDB在确定性密文列上构建标准的B-tree索引. 基于该索引可高效地进行密文等值查询、等值连接和分组(grouping)操作.TEE模式下, GaussDB借助TEE enclave比较随机密文的顺序, 从而在随机密文列上构建B-tree索引. 在执行范围查询时, 借助TEE遍历B-tree索引(将被查询的密文和索引keys发送到enclave中比较大小), 并获取匹配的结果. 由于软件模式是在确定性密文上构建的索引, 这暴露了密文的等值频率信息. 因此GaussDB的软硬融合的模式在某种程度上牺牲了一些安全性, 以换取灵活性和性能.
软硬融合的全密态数据库是最近两年刚刚出现的一种新型架构. 除GaussDB之外, 虽然也有一些基于TEE的全密态数据库(如微软的Azure[2]), 能够支持基于软件加密算法的密文等值查询, 但它们的软件模式与TEE模式是两个完全独立模式, 不能像GaussDB那样自适应地根据SQL查询来选择模式. 并且, 它们的软件模式仅支持密文的等值查询, 因此严格来说不能算是软硬融合模式.
6 全密态数据库的访问模式保护关键技术加密虽然能够对敏感数据的机密性提供一定的保护, 但还不能够保障明文信息完全不被泄漏. 攻击者还能够通过分析访问模式(access pattern)推断出部分重要信息. 访问模式是指访问的类型(读或写), 以及被访问的内存地址或查询的返回结果. 例如, 在Islam等人[117]的实验中, 攻击者仅通过观察加密电子邮件数据库的访问模式(查询对应的返回结果), 就可以确定多达80%的邮件搜索查询是否包含某个已知关键词.
6.1 基于软件的访问模式保护保护访问模式要求数据以不经意的(oblivious)方式被访问, 让攻击者不能区分客户端的访问类型和被访问的数据. 不经意随机访问机(oblivious RAM, ORAM)是研究的最广泛的一类不经意访问方案. ORAM最早由Coldreich和Ostrovsky[118, 119]提出, 允许客户端在不泄露其访问模式的情况下访问服务器上的加密数据. 为了隐藏访问的类型, ORAM通常将读取和写入作为原子操作一起执行. 当客户端读取数据时, ORAM也会将其写回. 写入数据时, ORAM先读取内容, 再更新内容, 最后写回. 为了隐藏访问地址, ORAM通常将真实数据和附加的虚拟数据一起存储在服务器上. ORAM总是读取或写入比实际需要的数据多的数据, 以防止攻击者发现客户端真正要访问的数据. 由于ORAM引入了额外的操作, 导致客户端和服务器的存储、带宽以及查询开销都很高, 因此相关的研究主要围绕着如何提高其性能展开. 研究者通过将ORAM的工作原理与不同的数据结构相结合, 在服务端使用不同的数据结构存储ORAM数据单元(数据桶、数据块等), 在客户端存储元数据和缓存数据, 并设计两端的ORAM访问协议, 从而产生了多种ORAM模型, 包括简单模型[119]、平方根模型[119]、层次模型[119]、分区模型[120]和树状模型[121−124]. 其中树状模型的性能相对较好, 每次访问最多遍历树的层高个数据单元. 因此近几年的ORAM方案大多基于树状模型, 如典型的Path-ORAM[122].
利用不经意访问技术, 全密态数据库在保护访问模式方面的研究可以分为以下几类.
(1) 保护连接操作的访问模式
2008年Li等人[125]首先提出了不经意连接方案, 但他们的算法的效率都等价于笛卡尔积. 2014年Arasu等人[126]提出了可支持多种数据库查询操作的不经意访问方案, 不过Krastnikov等人[127]指出该方案的细节不完整, 作者也没有提供可验证其实验结果的原型实现. 2020年Krastnikov等人[127] 提出了一种用于一般二元等值连接的不经意算法. 不过, Chang等人[128]指出该算法不容易扩展到不经意多表连接, 一系列不经意二元连接会泄露中间表的大小, 这可能会泄漏一些敏感信息, 例如数据分布或中间连接图的稀疏性. 2022年Chang等人[128]提出了一个解决通用(非主-外键连接)的二元或多元等值连接方案. 该方案将oblivious B-tree索引[116,129]与Path-ORAM[122]相结合, 在连接处理中通过oblivious B-tree检索数据块, 解决了以不经意的方式计算连接函数的问题. 他们的方案比非不经意访问的方式, 有大约10倍的存储空间开销和数十到数百倍的查询开销.
(2) 保护聚集操作的访问模式
2020年Hackenjos等人[130]提出了一个保护访问模式的多属性GROUP BY聚集操作的SAGMA方案, 支持COUNT, SUM和AVERAGE操作. 该方案利用SWHE和SSE实现了密文上的GROUP BY聚集操作, 并利用其设计的分桶算法实现了访问模式保护. 桶内的数据由SSE算法确定, 通过使用映射函数移动桶内的加密值并对移动后的值求和来完成聚集操作. 安全性上, SAGMA保护了密文的等值频率和访问模式, 但会暴露桶的访问频率. 此外, 由于使用了SSE算法, SAGMA会通过查询token暴露搜索模式(search pattern). 效率上, 根据Hackenjos等人[130]的实验, 在大小为
2022年Ren等人[131]提出了基于FHE的保护访问模式的多属性聚集方案HEDA, 支持COUNT, SUM和AVERAGE. 并且不限于GROUP BY, 理论上可支持IN, BETWEEN, EXIST, ANY, ALL等查询条件. 以SUM为例, 聚集查询的过程分为3个步骤: 1)比较. 扫描所有行, 并在临时表里记录这些行是否符合查询条件. 符合查询条件的行值标记为[0], 不符合条件的标记为[1] (中括号表示这些标记被FHE加密); 2)相乘. 将待聚合列的密文数值与标记密文[0]或[1]相乘, 不符合条件的相乘后结果为0, 符合条件的相乘后结果仍是原值; 3)求和. 将相乘后的密文累加起来即为SUM的密文结果. 安全性上, HEDA设计了基于FHE的安全协议, 保护了等值频率、访问模式和搜索模式, 因此安全性极高. 性能上, 在Ren等人[131]的实验中
(3) 保护范围查询的访问模式
2019年Asharov等人[132]和Chakraborti等人[133]都提出了支持不经意范围查询的Range ORAM方案, 基本原理非常相似. Range ORAM将ORAM与范围树(range tree)结合, 通过逻辑的范围树将完整的范围拆分成多个子范围, 并在服务端为每个子范围都存储一个单独的ORAM. 查询时, 客户端需要借助辅助数据结构来完成查询. 该辅助数据结构也存储在服务端的一个ORAM内, 可以被视为不经意二叉搜索树的变种. Range ORAM需要很大的存储成本, 对于大小为N的范围空间, 需要存储logN+1个单独ORAM. 同时也会带来很大的带宽和磁盘I/O开销. 此外, Range ORAM只适用于键值形式的数据, 不适用于多列形式的关系型数据库.
2022年Change等人[129]提出了基于Path-ORAM和B-tree索引的不经意范围查询方案. 其基本思想是忽略B-tree索引和ORAM数据块的语义差异, 将所有块存储到 Path-ORAM 结构中. 我们知道, B-tree中的每个节点都存储在一个磁盘页中, 指向子节点的指针是页ID. 因此可以把页ID作为ORAM块ID, 页作为ORAM块, 这样, 服务端的Path-ORAM树状结构就构建在加密的B-tree索引块和数据块之上, 查询时从根块开始向下遍历Path-ORAM树形结构来检索数据, 过程与遍历标准B-tree相同, 唯一的区别是通过ORAM协议检索索引和数据块. 如果将B-tree换成R-tree, 该方案也适用于k近邻查询.
6.2 基于可信硬件TEE的访问模式保护由于不经意访问极高的开销, 基于软件的访问模式保护通常只能保护某个特定的操作, 如上面介绍的连接、聚集、范围查询等. 可信硬件TEE的出现使得通用型的访问模式保护成为可能, 这得益于TEE enclave是可信的, 可以作为客户端的一部分. ORAM的客户端能够运行在enclave中, ORAM的服务端运行在REE中. 这样ORAM客户端和服务端之间的交互发生在一台机器内, 不需要通过网络, 大大地降低了网络带宽成本和通信延迟时间. 近几年出现了支持多种数据库操作的不经意访问方案, 典型的代表是Opaque[134]. Opaque由Zheng等人在2017年提出, 是一个基于Spark的分布式数据分析平台, 支持广泛的查询操作, 并保护查询的访问模式. 为支持分布式, Opaque引入了新的分布式不经意关系运算符, 以及用于优化这些新运算符的新查询规划技术. Zheng等人称, 与之前最先进的不经意协议相比, Opaque有3个数量级的性能提升.
一些基于可信硬件TEE的全密态数据库支持通过不经意访问来保护访问模式, 如前文介绍的CipherBase[110]和ObliDB[116]. CipherBase[110]提出了隐藏访问模式的不经意运算符, 为所有关系运算符设计了不经意的实现. 例如, 通过使用不经意的排序运算符来防止排序过程中的访问模式泄露. 不过CipherBase没有给出具体的实现和性能数据. ObliDB[116]指出Opaque[134]和CipherBase[110]都需要扫描整个表来完成不经意查询, 效率较低. ObliDB[116]提出了基于ORAM的oblivious B+tree索引, 来提高不经意查询效率, 与 Opaque相比性能提升了19倍.
7 全密态数据库关键技术的未来研究方向与挑战随着云计算的蓬勃发展, 云数据安全越来越被重视, 全密态数据库的相关技术在学术界和工业界一直是多年以来的研究热点, 产生了多种不同类型的全密态数据库, 包括基于软件加密算法全密态数据库、基于可信硬件TEE的全密态数据库以及软硬融合的全密态数库. 尽管相关技术经过了多年的研究和发展, 但仍然有很多问题有待进一步的研究和解决.
7.1 基于软件加密算法的全密态数据库基于软件加密算法的全密态数据库不需要依赖指定硬件, 可以在一般的云主机上运行, 有较好的通用性. 不过加密算法会带来额外的开销, 需要较多的存储和计算资源. 现有的加密方案都还不是全密态数据库的最优解决方案, 要么因为安全性不够, 或者空间占用率高、计算开销大, 或者能够支持的数据库操作有限. 因此, 需要设计更好的加密方案, 以提供更好的安全性, 并在功能和性能之间取得平衡. 特别地, 目前具有可实践性的加密方案大多只适用部分运算, 导致纯软的全密态数据库需要使用多个加密方案才能支持主要的数据库运算. 这样不仅增加了设计和开发的难度, 也增加了存储和计算的开销. 因此, 如何让通用加密方案(如全同态加密)具有可实践性, 将是重要的长期性的挑战.
对称可搜索加密方案(SSE)具有相对较好的安全性和较丰富的功能性, 可支持等值查询、范围查询, 以及字符串模糊查询等操作, 是最近几年的研究热点. 不过相比于确定性加密、保序加密、布隆过滤器等方案, SSE的密文空间膨胀较高, 具有较大的存储开销, 会导致运算性能的下降. 如何能降低其存储开销是一项复杂的挑战.
半同态加密(PHE)可以有效地支持数据库的聚合运算, 但效率不高. 传统的PHE方案大多基于非对称加密算法实现, 如Paillier和ElGamal. 近几年研究者提出了一些基于对称加密算法的PHE方案, 以加快其运算速度, 如ASHE和Symmetria. 也有研究者通过如并发缓存的系统优化方式加快PHE的运算效率. 不过距离高效计算仍然有不小的差距. 提升PHE的效率仍是未来的研究方向和挑战.
此外, 随着数据库处理的数据量越来越大, 单机数据库的应用场景已越来越少, 集群数据库与分布式数据库已成为主流. 但有的加密方案, 如基于索引的SSE加密方案, 索引大多集中存储, 不利于非单机的应用场景. 如何让这类加密方案适用于多点或分布式的场景, 将是一项挑战.
7.2 基于可信硬件TEE的全密态数据库可信硬件TEE在不受信任的云服务端开辟了一小块受信任的区域, 使得敏感数据能够在TEE内解密成明文, 并做各种数据库运算. 基于明文运算的TEE几乎可以支持所有的数据库操作, 大大降低了全密态数据库的设计复杂度和开发成本, 并且也有较好的性能. 不过, 现有的基于TEE的全密态数据库大多是在传统数据库的基础上修改而来的, 可能无法与TEE完美集成并发挥TEE的所有特性. 如何基于TEE的特性, 实现一个TEE原生的全密态数据库将是一项挑战. 此外, TEE与REE之间的交互成本非常高昂, 如何减少交互次数和数据交换量是提高全密态数据库性能的重要方向.
7.3 软硬融合的全密态数据库软硬融合的全密态数据库融合了软件加密算法和可信硬件TEE双方的优点, 将部分查询操作利用加密算法和REE加密索引在REE下执行, 部分操作利用可信硬件和TEE加密索引在TEE下执行, 显著地降低REE和TEE之间的交互开销. 不过, 现有的软硬融合的解决方案, 软件部分和硬件部分独立运算, 没有相互补充. 如何利用REE和TEE各自的优势来协同查询处理是一个挑战. 例如, 如果REE能在将加密数据发送到TEE之前过滤掉大量不相关的数据, 就可以大大减少REE于TEE之间的交互次数和交互数据量. 此外, 现有软件部分的加密算法大多基于确定性加密, 安全性不高. 如何在保障性能的前提下, 增加软件部分算法的安全性, 将是一项挑战.
7.4 访问模式保护加密虽然能够对敏感数据的机密性提供一定的保护, 但还不能够保障明文信息完全不被泄漏, 攻击者还能够通过分析访问模式推断出部分重要信息. 访问模式保护可以让数据以不经意的方式被访问, 让攻击者不能区分客户端的访问类型和被访问的数据. 不经意访问技术发展了多年, 但其性能仍然较低. 尽管可信硬件TEE的出现, 使得通用型的访问模式保护成为可能, 但目前大多数方案仅应用在研究型的全密态数据库中, 而工业界的数据库对访问模式保护的仍然很少. 如何提高不经意访问方案的效率, 使之具有更好的可实践性, 是一项长期的挑战.
8 结束语数据被称为“新时代的石油”, 保护外包到云数据库中的数据安全与隐私成为重要的研究课题, 全密态数据库在这个样的背景下应运而生. 本文对全密态数据库的关键技术做了系统性的综述, 首先总结了全密态数据的应用场景和3种主要的架构. 之后对3种架构的关键技术做了细致的阐述, 包括基于软件加密方案的关键技术、基于可信硬件TEE的关键技术, 以及软硬融合的全密态数据库. 此外, 还介绍了保护访问模式的关键技术. 最后对未来的研究趋势做了展望. 希望本综述能为今后的研究者提供有价值的参考.
| [1] |
Do Q, Martini B, Choo KKR. The role of the adversary model in applied security research. Computers & Security, 2019, 81: 156-181.
[doi:10.1016/j.cose.2018.12.002] |
| [2] |
Antonopoulos P, Arasu A, Singh KD, Eguro K, Gupta N, Jain R, Kaushik R, Kodavalla H, Kossmann D, Ogg N, Ramamurthy R, Szymaszek J, Trimmer J, Vaswani K, Venkatesan R, Zwilling M. Azure SQL database always encrypted. In: Proc. of the 2020 ACM SIGMOD Int’l Conf. on Management of Data. Portland: ACM, 2020. 1511–1525. [doi: 10.1145/3318464.3386141]
|
| [3] |
Sun YY, Wang S, Li HR, Li FF. Building enclave-native storage engines for practical encrypted databases. Proc. of the VLDB Endowment, 2021, 14(6): 1019–1032. [doi: 10.14778/3447689.3447705]
|
| [4] |
Zhu JW, Cheng K, Liu JY, Guo L. Full encryption: An end to end encryption mechanism in GaussDB. Proc. of the VLDB Endowment, 2021, 14(12): 2811-2814.
[doi:10.14778/3476311.3476351] |
| [5] |
Naveed M, Kamara S, Wright CV. Inference attacks on property-preserving encrypted databases. In: Proc. of the 22nd ACM SIGSAC Conf. on Computer and Communications Security. Denver: ACM, 2015. 644–655. [doi: 10.1145/2810103.2813651]
|
| [6] |
Grubbs P, Lacharite MS, Minaud B, Paterson KG. Pump up the volume: Practical database reconstruction from volume leakage on range queries. In: Proc. of the 2018 ACM SIGSAC Conf. on Computer and Communications Security. Toronto: ACM, 2018. 315–331. [doi: 10.1145/3243734.3243864]
|
| [7] |
Gui ZC, Johnson O, Warinschi B. Encrypted databases: New volume attacks against range queries. In: Proc. of the 2019 ACM SIGSAC Conf. on Computer and Communications Security. London: ACM, 2019. 361–378. [doi: 10.1145/3319535.3363210]
|
| [8] |
Grubbs P, Sekniqi K, Bindschaedler V, Naveed M, Ristenpart T. Leakage-abuse attacks against order-revealing encryption. In: Proc. of the 2017 IEEE Symp. on Security and Privacy (SP). San Jose: IEEE, 2017. 655–672. [doi: 10.1109/SP.2017.44]
|
| [9] |
Blackstone L, Kamara S, Moataz T. Revisiting leakage abuse attacks. In: Proc. of the 27th Annual Network and Distributed System Security Symp. San Diego: The Internet Society, 2020. 1–43.
|
| [10] |
Cash D, Grubbs P, Perry J, Ristenpart T. Leakage-abuse attacks against searchable encryption. In: Proc. of the 22nd ACM SIGSAC Conf. on Computer and Communications Security. Denver: ACM, 2015. 668–679. [doi: 10.1145/2810103.2813700]
|
| [11] |
Goldwasser S, Micali S. Probabilistic encryption & how to play mental poker keeping secret all partial information. In: Proc. of the 14th Annual ACM Symp. on Theory of Computing. San Francisco: ACM, 1982. 365–377. [doi: 10.1145/800070.802212]
|
| [12] |
Goldwasser S, Micali S. Probabilistic encryption. Journal of Computer and System Sciences, 1984, 28(2): 270-299.
[doi:10.1016/0022-0000(84)90070-9] |
| [13] |
MongoDB. Client-side field level encryption—MongoDB manual. 2023. https://www.mongodb.com/docs/rapid/core/csfle/
|
| [14] |
Song DX, Wagner D, Perrig A. Practical techniques for searches on encrypted data. In: Proc. of the 2000 IEEE Symp. on Security and Privacy. Berkeley: IEEE, 2000. 44–55. [doi: 10.1109/SECPRI.2000.848445]
|
| [15] |
Goh EJ. Secure indexes. Cryptology ePrint archive. Paper 2003/216, 2003. https://eprint.iacr.org/2003/216
|
| [16] |
Curtmola R, Garay J, Kamara S, Ostrovsky R. Searchable symmetric encryption: Improved definitions and efficient constructions. Journal of Computer Security, 2011, 19(5): 895-934.
[doi:10.5555/2590701.2590705] |
| [17] |
Chase M, Kamara S. Structured encryption and controlled disclosure. In: Proc. of the 16th Int’l Conf. on the Theory and Application of Cryptology and Information Security. Singapore: Springer, 2010. 577–594. [doi: 10.1007/978-3-642-17373-8_33]
|
| [18] |
van Liesdonk P, Sedghi S, Doumen J, Hartel P, Jonker W. Computationally efficient searchable symmetric encryption. In: Proc. of the 7th VLDB Workshop on Secure Data Management. Singapore: Springer, 2010. 87–100. [doi: 10.1007/978-3-642-15546-8_7]
|
| [19] |
Kamara S, Papamanthou C, Roeder T. Dynamic searchable symmetric encryption. In: Proc. of the 2012 ACM Conf. on Computer and Communications Security. Raleigh North: ACM, 2012. 965–976. [doi: 10.1145/2382196.2382298]
|
| [20] |
Cash D, Jarecki S, Jutla C, Krawczyk H, Roşu MC, Steiner M. Highly-scalable searchable symmetric encryption with support for boolean queries. In: Proc. of the 33rd Annual Int’l Cryptology Conf. Santa Barbara: Springer, 2013. 353–373. [doi: 10.1007/978-3-642-40041-4_20]
|
| [21] |
Kamara S, Papamanthou C. Parallel and dynamic searchable symmetric encryption. In: Proc. of the 17th Int’l Conf. on Financial Cryptography and Data Security. Okinawa: Springer, 2013. 258–274. [doi: 10.1007/978-3-642-39884-1_22]
|
| [22] |
Cash D, Jaeger J, Jarecki S, Jutla CS, Krawczyk H, Roşu MC, Steiner M. Dynamic searchable encryption in very-large databases: Data structures and implementation. In: Proc. of the 21st Annual Network and Distributed System Security Symp. San Diego: The Internet Society, 2014.
|
| [23] |
Stefanov E, Papamanthou C, Shi E. Practical dynamic searchable encryption with small leakage. In: Proc. of the 21st Annual Network and Distributed System Security Symp. San Diego: The Internet Society, 2014.
|
| [24] |
Naveed M, Prabhakaran M, Gunter CA. Dynamic searchable encryption via blind storage. In: Proc. of the 2014 IEEE Symp. on Security and Privacy. Berkeley: IEEE, 2014. 639–654. [doi: 10.1109/SP.2014.47]
|
| [25] |
Bösch C, Hartel P, Jonker W, Peter A. A survey of provably secure searchable encryption. ACM Computing Surveys, 2014, 47(2): 18.
[doi:10.1145/2636328] |
| [26] |
Bost R. ∑oφoς: Forward secure searchable encryption. In: Proc. of the 2016 ACM SIGSAC Conf. on Computer and Communications Security. Vienna: ACM, 2016. 1143–1154. [doi: 10.1145/2976749.2978303]
|
| [27] |
Bost R, Minaud B, Ohrimenko O. Forward and backward private searchable encryption from constrained cryptographic primitives. In: Proc. of the 2017 ACM SIGSAC Conf. on Computer and Communications Security. Dallas: ACM, 2017. 1465–1482. [doi: 10.1145/3133956.3133980]
|
| [28] |
George M, Kamara S, Moataz T. Structured encryption and dynamic leakage suppression. In: Proc. of the 40th Annual Int’l Conf. on the Theory and Applications of Cryptographic Techniques. Zagreb: Springer, 2021. 370–396. [doi: 10.1007/978-3-030-77883-5_13]
|
| [29] |
Li J, Huang YY, Wei Y, Lv SY, Liu ZL, Dong CY, Lou WJ. Searchable symmetric encryption with forward search privacy. IEEE Trans. on Dependable and Secure Computing, 2021, 18(1): 460-474.
[doi:10.1109/TDSC.2019.2894411] |
| [30] |
Chamani JG, Papadopoulos D, Karbasforushan M, Demertzis I. Dynamic searchable encryption with optimal search in the presence of deletions. In: Proc. of the 31st USENIX Security Symp. USENIX Association, 2022. 2425–2442.
|
| [31] |
Sharma D. Searchable encryption : A survey. Information Security Journal: A Global Perspective, 2023, 32(2): 76-119.
[doi:10.1080/19393555.2022.2033367] |
| [32] |
Minaud B, Reichle M. Dynamic local searchable symmetric encryption. In: Proc. of the 42nd Annual Int’l Cryptology Conf. Santa Barbara: Springer, 2022. 91–120. [doi: 10.1007/978-3-031-15985-5_4]
|
| [33] |
Falzon F, Markatou EA, Espiritu Z, Tamassia R. Range search over encrypted multi-attribute data. Proc. of the VLDB Endowment, 2022, 16(4): 587-600.
[doi:10.14778/3574245.3574247] |
| [34] |
Demertzis I, Papadopoulos S, Papapetrou O, Deligiannakis A, Garofalakis M. Practical private range search revisited. In: Proc. of the 2016 Int’l Conf. on Management of Data. San Francisco: ACM, 2016. 185–198. [doi: 10.1145/2882903.2882911]
|
| [35] |
Suga T, Nishide T, Sakurai K. Secure keyword search using bloom filter with specified character positions. In: Proc. of the 6th Int’l Conf. on Provable Security. Chengdu: Springer, 2012. 235–252.
|
| [36] |
Hacigümüş H, Iyer B, Li C, Mehrotra S. Executing SQL over encrypted data in the database-service-provider model. In: Proc. of the 2002 ACM SIGMOD Int’l Conf. on Management of Data. Madison: ACM, 2002. 216–227. [doi: 10.1145/564691.564717]
|
| [37] |
Hore B, Mehrotra S, Tsudik G. A privacy-preserving index for range queries. In: Proc. of the 30th Int’l Conf. on Very Large Data Bases. Toronto: Morgan Kaufmann, 2004. 720–731.
|
| [38] |
Hore B, Mehrotra S, Canim M, Kantarcioglu M. Secure multidimensional range queries over outsourced data. The VLDB Journal, 2012, 21(3): 333-358.
[doi:10.1007/s00778-011-0245-7] |
| [39] |
Agrawal R, Kiernan J, Srikant R, Xu YR. Order preserving encryption for numeric data. In: Proc. of the 2004 ACM SIGMOD Int’l Conf. on Management of Data. Paris: ACM, 2004. 563–574. [doi: 10.1145/1007568.1007632]
|
| [40] |
Boldyreva A, Chenette N, Lee Y, O’Neill A. Order-preserving symmetric encryption. In: Proc. of the 28th Annual Int’l Conf. on the Theory and Applications of Cryptographic Techniques. Cologne: Springer, 2009. 224–241. [doi: 10.1007/978-3-642-01001-9_13]
|
| [41] |
Boldyreva A, Chenette N, O’Neill A. Order-preserving encryption revisited: Improved security analysis and alternative solutions. In: Proc. of the 31st Annual Int’l Cryptology Conf. Santa Barbara: Springer, 2011. 578–595. [doi: 10.1007/978-3-642-22792-9_33]
|
| [42] |
Liu DX, Wang SL. Programmable order-preserving secure index for encrypted database query. In: Proc. of the 5th IEEE Int’l Conf. on Cloud Computing. Honolulu: IEEE, 2012. 502–509. [doi: 10.1109/CLOUD.2012.65]
|
| [43] |
Popa RA, Li FH, Zeldovich N. An ideal-security protocol for order-preserving encoding. In: Proc. of the 2013 IEEE Symp. on Security and Privacy. Berkeley: IEEE, 2013. 463–477. [doi: 10.1109/SP.2013.38]
|
| [44] |
Mavroforakis C, Chenette N, O’Neill A, Kollios G, Canetti R. Modular order-preserving encryption, revisited. In: Proc. of the 2015 ACM SIGMOD Int’l Conf. on Management of Data. Melbourne: ACM, 2015. 763–777. [doi: 10.1145/2723372.2749455]
|
| [45] |
Roche DS, Apon D, Choi SG, Yerukhimovich A. POPE: Partial order preserving encoding. In: Proc. of the 2016 ACM SIGSAC Conf. on Computer and Communications Security. Vienna: ACM, 2016. 1131–1142. [doi: 10.1145/2976749.2978345]
|
| [46] |
Li DJ, Lv SY, Huang YY, Liu YJ, Li T, Liu ZL, Guo L. Frequency-hiding order-preserving encryption with small client storage. Proc. of the VLDB Endowment, 2021, 14(13): 3295-3307.
[doi:10.14778/3484224.3484228] |
| [47] |
Tian HL, Zhang Y, Li C, Xing CX. A survey of confidentiality protection for cloud databases. Chinese Journal of Computers, 2017, 40(10): 2245-2270(in Chinese with English abstract).
[doi:10.11897/SP.J.1016.2017.02245] |
| [48] |
Kerschbaum F. Frequency-hiding order-preserving encryption. In: Proc. of the 22nd ACM SIGSAC Conf. on Computer and Communications Security. Denver: ACM, 2015. 656–667. [doi: 10.1145/2810103.2813629]
|
| [49] |
Bogatov D, Kollios G, Reyzin L. A comparative evaluation of order-revealing encryption schemes and secure range-query protocols. Proc. of the VLDB Endowment, 2019, 12(8): 933-947.
[doi:10.14778/3324301.3324309] |
| [50] |
Boneh D, Lewi K, Raykova M, Sahai A, Zhandry M, Zimmerman J. Semantically secure order-revealing encryption: Multi-input functional encryption without obfuscation. In: Proc. of the 34th Annual Int’l Conf. on the Theory and Applications of Cryptographic Techniques. Sofia: Springer, 2015. 563–594. [doi: 10.1007/978-3-662-46803-6_19]
|
| [51] |
Chenette N, Lewi K, Weis SA, Wu DJ. Practical order-revealing encryption with limited leakage. In: Proc. of the 23rd Int’l Conf. on Fast Software Encryption. Bochum: Springer, 2016. 474–493. [doi: 10.1007/978-3-662-52993-5_24]
|
| [52] |
Lewi K, Wu DJ. Order-revealing encryption: New constructions, applications, and lower bounds. In: Proc. of the 2016 ACM SIGSAC Conf. on Computer and Communications Security. Vienna Vienna: ACM, 2016. 1167–1178. [doi: 10.1145/2976749.2978376]
|
| [53] |
Liu ZL, Lv SY, Li J, Huang YY, Guo L, Yuan YL, Dong CY. EncodeORE: Reducing leakage and preserving practicality in order-revealing encryption. IEEE Trans. on Dependable and Secure Computing, 2022, 19(3): 1579-1591.
[doi:10.1109/TDSC.2020.3029845] |
| [54] |
Durak FB, DuBuisson TM, Cash D. What else is revealed by order-revealing encryption? In: Proc. of the 2016 ACM SIGSAC Conf. on Computer and Communications Security. Vienna: ACM, 2016. 1155–1166. [doi: 10.1145/2976749.2978379]
|
| [55] |
Hu CH, Han LD, Yiu SM. Efficient and secure multi-functional searchable symmetric encryption schemes. Security and Communication Networks, 2016, 9(1): 34-42.
[doi:10.1002/sec.1376] |
| [56] |
Bösch C, Brinkman R, Hartel P, Jonker W. Conjunctive wildcard search over encrypted data. In: Proc. of the 8th VLDB Workshop on Secure Data Management. Seattle: Springer, 2011. 114–127. [doi: 10.1007/978-3-642-23556-6_8]
|
| [57] |
Liu JL, Qin J, Wang Q, Zhao B, Zhang Q, Su Y. On complex semantic searchable encryptions. Journal of Cryptologic Research, 2022, 9(1): 1-22(in Chinese with English abstract).
[doi:10.13868/j.cnki.jcr.000500] |
| [58] |
Hu CH, Han LD. Efficient wildcard search over encrypted data. Int’l Journal of Information Security, 2016, 15(5): 539-547.
[doi:10.1007/s10207-015-0302-0] |
| [59] |
Bloom BH. Space/time trade-offs in hash coding with allowable errors. Communications of the ACM, 1970, 13(7): 422-426.
[doi:10.1145/362686.362692] |
| [60] |
Chatterjee S, Kesarwani M, Modi J, Mukherjee S, Parshuram Puria SK, Shah A. Secure and efficient wildcard search over encrypted data. Int’l Journal of Information Security, 2021, 20(2): 199-244.
[doi:10.1007/s10207-020-00492-w] |
| [61] |
Yang Y, Liu XM, Deng RH, Weng J. Flexible wildcard searchable encryption system. IEEE Trans. on Services Computing, 2020, 13(3): 464-477.
[doi:10.1109/TSC.2017.2714669] |
| [62] |
Liu J, Zhao B, Qin J, Zhang X, Ma JX. Multi-keyword ranked searchable encryption with the wildcard keyword for data sharing in cloud computing. The Computer Journal, 2023, 66(1): 184-196.
[doi:10.1093/comjnl/bxab153] |
| [63] |
Li Y, Ning JT, Chen J. Secure and practical wildcard searchable encryption system based on inner product. IEEE Trans. on Services Computing, 2023, 16(3): 2178-2190.
[doi:10.1109/TSC.2022.3207750] |
| [64] |
Li J, Wang Q, Wang C, Cao N, Ren K, Lou WJ. Fuzzy keyword search over encrypted data in cloud computing. In: Proc. of the 2010 IEEE INFOCOM. San Diego: IEEE, 2010. 1–5. [doi: 10.1109/INFCOM.2010.5462196]
|
| [65] |
Liu C, Zhu LH, Li LYJ, Tan YA. Fuzzy keyword search on encrypted cloud storage data with small index. In: Proc. of the 2011 IEEE Int’l Conf. on Cloud Computing and Intelligence Systems. Beijing: IEEE, 2011. 269–273. [doi: 10.1109/CCIS.2011.6045073]
|
| [66] |
Wang JF, Ma H, Tang Q, Li J, Zhu H, Ma S, Chen XF. Efficient verifiable fuzzy keyword search over encrypted data in cloud computing. Computer Science and Information Systems, 2013, 10(2): 667-684.
[doi:10.2298/CSIS121104028W] |
| [67] |
Kuzu M, Islam MS, Kantarcioglu M. Efficient similarity search over encrypted data. In: Proc. of the 28th IEEE Int’l Conf. on Data Engineering. Arlington: IEEE, 2012. 1156–1167. [doi: 10.1109/ICDE.2012.23]
|
| [68] |
Wang B, Yu SC, Lou WJ, Hou YT. Privacy-preserving multi-keyword fuzzy search over encrypted data in the cloud. In: Proc. of the 2014 IEEE Conf. on Computer Communications. Toronto: IEEE, 2014. 2112–2120. [doi: 10.1109/INFOCOM.2014.6848153]
|
| [69] |
Fu ZJ, Wu XL, Guan CW, Sun XM, Ren K. Toward efficient multi-keyword fuzzy search over encrypted outsourced data with accuracy improvement. IEEE Trans. on Information Forensics and Security, 2016, 11(12): 2706-2716.
[doi:10.1109/TIFS.2016.2596138] |
| [70] |
Zhong H, Li ZF, Cui J, Sun Y, Liu L. Efficient dynamic multi-keyword fuzzy search over encrypted cloud data. Journal of Network and Computer Applications, 2020, 149: 102469.
[doi:10.1016/j.jnca.2019.102469] |
| [71] |
ElGamal T. A public key cryptosystem and a signature scheme based on discrete logarithms. In: Blakley GR, Chaum D, eds. Advances in Cryptology. Berlin, Heidelberg: Springer, 1985. 10–18. [doi: 10.1007/3-540-39568-7_2]
|
| [72] |
Paillier P. Public-key cryptosystems based on composite degree residuosity classes. In: Proc. of the 1999 Int’l Conf. on the Theory and Application of Cryptographic Techniques. Prague: Springer, 1999. 223–238. [doi: 10.1007/3-540-48910-X_16]
|
| [73] |
Sidorov V, Wei EYF, Ng WK. Comprehensive performance analysis of homomorphic cryptosystems for practical data processing. arXiv:2202.02960, 2022.
|
| [74] |
Papadimitriou A, Bhagwan R, Chandran N, Ramjee R, Haeberlen A, Singh H, Modi A, Badrinarayanan S. Big data analytics over encrypted datasets with seabed. In: Proc. of the 12th USENIX Conf. on Operating Systems Design and Implementation. Savannah: USENIX Association, 2016. 587–602. [doi: 10.5555/3026877.3026922]
|
| [75] |
Savvides S, Khandelwal D, Eugster P. Efficient confidentiality-preserving data analytics over symmetrically encrypted datasets. Proc. of the VLDB Endowment, 2020, 13(8): 1290-1303.
[doi:10.14778/3389133.3389144] |
| [76] |
Timothy Tawose O, Dai J, Yang L, Zhao DF. Toward efficient homomorphic encryption for outsourced databases through parallel caching. Proc. of the ACM on Management of Data, 2023, 1(1): 66.
[doi:10.1145/3588920] |
| [77] |
Rivest RL, Adleman L, Dertouzos ML. On data banks and privacy homomorphisms. In: DeMillo RA, ed. Foundations of Secure Computation. New York: Academic Press, 1978. 169–179.
|
| [78] |
Gentry C. Fully homomorphic encryption using ideal lattices. In: Proc. of the 41st Annual ACM Symp. on Theory of Computing. Bethesda: ACM, 2009. 169–178. [doi: 10.1145/1536414.1536440]
|
| [79] |
Gentry C, Halevi S. Implementing gentry’s fully-homomorphic encryption scheme. In: Proc. of the 30th Annual Int’l Conf. on the Theory and Applications of Cryptographic Techniques. Tallinn: Springer, 2011. 129–148. [doi: 10.1007/978-3-642-20465-4_9]
|
| [80] |
Brakerski Z, Vaikuntanathan V. Efficient fully homomorphic encryption from (standard) LWE. In: Proc. of the 52nd IEEE Annual Symp. on Foundations of Computer Science. Palm Springs: IEEE, 2011. 97–106. [doi: 10.1109/FOCS.2011.12]
|
| [81] |
Brakerski Z, Gentry C, Vaikuntanathan V. (Leveled) fully homomorphic encryption without bootstrapping. In: Proc. of the 3rd Innovations in Theoretical Computer Science Conf. Cambridge: ACM, 2012. 309–325. [doi: 10.1145/2090236.2090262]
|
| [82] |
Fan JF, Vercauteren F. Somewhat practical fully homomorphic encryption. Cryptology ePrint Archive, Paper 2012/144, 2012. https://eprint.iacr.org/2012/144
|
| [83] |
Gentry C, Sahai A, Waters B. Homomorphic encryption from learning with errors: Conceptually-simpler, asymptotically-faster, attribute-based. In: Proc. of the 33rd Annual Int’l Cryptology Conf. Santa Barbara: Springer, 2013. 75–92. [doi: 10.1007/978-3-642-40041-4_5]
|
| [84] |
Ducas L, Micciancio D. FHEW: Bootstrapping homomorphic encryption in less than a second. In: Proc. of the 34th Annual Int’l Conf. on the Theory and Applications of Cryptographic Techniques. Sofia: Springer, 2014. 617–640. [doi: 10.1007/978-3-662-46800-5_24]
|
| [85] |
Chillotti I, Gama N, Georgieva M, Izabachène M. Faster fully homomorphic encryption: Bootstrapping in less than 0.1 seconds. In: Proc. of the 22nd Int’l Conf. on the Theory and Application of Cryptology and Information Security. Hanoi: Springer, 2016. 3–33. [doi: 10.1007/978-3-662-53887-6_1]
|
| [86] |
Cheon JH, Kim A, Kim M, Song Y. Homomorphic encryption for arithmetic of approximate numbers. In: Proc. of the 23rd Int’l Conf. on the Theory and Application of Cryptology and Information Security. Hong Kong: Springer, 2017. 409–437. [doi: 10.1007/978-3-319-70694-8_15]
|
| [87] |
Yao AC. Protocols for secure computations. In: Proc. of the 23rd Annual Symp. on Foundations of Computer Science. Chicago: IEEE, 1982. 160–164. [doi: 10.1109/SFCS.1982.38]
|
| [88] |
Yao ACC. How to generate and exchange secrets. In: Proc. of the 27th Annual Symp. on Foundations of Computer Science. Toronto: IEEE, 1986. 162–167. [doi: 10.1109/SFCS.1986.25]
|
| [89] |
Goldwasser S, Kalai Y, Popa RA, Vaikuntanathan V, Zeldovich N. Reusable garbled circuits and succinct functional encryption. In: Proc. of the 45th Annual ACM Symp. on Theory of Computing. Palo Alto: ACM, 2013. 555–564. [doi: 10.1145/2488608.2488678]
|
| [90] |
Saleem A, Khan A, Shahid F, Masoom Alam M, Khan MK. Recent advancements in garbled computing: How far have we come towards achieving secure, efficient and reusable garbled circuits. Journal of Network and Computer Applications, 2018, 108: 1-19.
[doi:10.1016/j.jnca.2018.02.006] |
| [91] |
Zhao QS, Liu XM, Xu HL, Li YB. Practical reusable garbled circuits with parallel updates. Computer Standards & Interfaces, 2023, 86: 103721.
[doi:10.1016/j.csi.2023.103721] |
| [92] |
Harth-Kitzerow C, Carle G, Fei F, Luckow A, Klepsch J. CRGC: A practical framework for constructing reusable garbled circuits. In: Proc. of the 19th Int’l Conf. on Security and Cryptography. Lisbon: SciTePress, 2022. 83–95. [doi: 10.5220/0011145300003283]
|
| [93] |
Popa RA, Redfield CMS, Zeldovich N, Balakrishnan H. CryptDB: Protecting confidentiality with encrypted query processing. In: Proc. of the 23rd ACM Symp. on Operating Systems Principles. Cascais: ACM, 2011. 85–100. [doi: 10.1145/2043556.2043566]
|
| [94] |
Popa RA, Zeldovich N, Balakrishnan H. CryptDB: A practical encrypted relational DBMS. 2011. https://people.csail.mit.edu/nickolai/papers/popa-cryptdb-tr.pdf
|
| [95] |
Popa RA, Redfield CMS, Zeldovich N, Balakrishnan H. CryptDB: Processing queries on an encrypted database. Communications of the ACM, 2012, 55(9): 103-111.
[doi:10.1145/2330667.2330691] |
| [96] |
Tu S, Kaashoek MF, Madden S, Zeldovich N. Processing analytical queries over encrypted data. Proc. of the VLDB Endowment, 2013, 6(5): 289-300.
[doi:10.14778/2535573.2488336] |
| [97] |
Pappas V, Krell F, Vo B, Kolesnikov V, Malkin T, Choi SG, George W, Keromytis A, Bellovin S. Blind seer: A scalable private DBMS. In: Proc. of the 2014 IEEE Symp. on Security and Privacy. Berkeley: IEEE, 2014. 359–374. [doi: 10.1109/SP.2014.30]
|
| [98] |
Poddar R, Boelter T, Popa RA. Arx: An encrypted database using semantically secure encryption. Proc. of the VLDB Endowment, 2019, 12(11): 1664-1678.
[doi:10.14778/3342263.3342641] |
| [99] |
MongoDB/Mongo: The MongoDB database. 2022. https://github.com/mongodb/mongo
|
| [100] |
Braund C, Borkar P. MongoDB. MongoDB releases queryable encryption preview. 2022. https://www.mongodb.com/blog/post/mongodb-releases-queryable-encryption-preview
|
| [101] |
Popa RA, Zeldovich N. Cryptographic treatment of CryptDB’s adjustable join. CSAIL. 2012. https://people.csail.mit.edu/nickolai/papers/popa-join-tr.pdf
|
| [102] |
Costan V, Devadas S. Intel SGX explained. Cryptology ePrint Archive, 2016. https://eprint.iacr.org/2016/086.pdf
|
| [103] |
McKeen F, Alexandrovich I, Berenzon A, Rozas CV, Shafi H, Shanbhogue V, Savagaonkar UR. Innovative instructions and software model for isolated execution. In: Proc. of the 2nd Int’l Workshop on Hardware and Architectural Support for Security and Privacy. Tel Aviv: ACM, 2013. 10. [doi: 10.1145/2487726.2488368]
|
| [104] |
AMD. AMD secure encrypted virtualization (sev). AMD. 2023. https://www.amd.com/en/developer/sev.html
|
| [105] |
Ngabonziza B, Martin D, Bailey A, Cho H, Martin S. TrustZone explained: Architectural features and use cases. In: Proc. of the 2nd IEEE Int’l Conf. on Collaboration and Internet Computing. Pittsburgh: IEEE, 2016. 445–451. [doi: 10.1109/CIC.2016.065]
|
| [106] |
Vinayagamurthy D, Gribov A, Gorbunov S. StealthDB: A scalable encrypted database with full SQL query support. Proc. on Privacy Enhancing Technologies, 2019, 2019(3): 370-388.
[doi:10.2478/popets-2019-0052] |
| [107] |
Priebe C, Vaswani K, Costa M. EnclaveDB: A secure database using SGX. In: Proc. of the 2018 IEEE Symp. on Security and Privacy. San Francisco: IEEE, 2018. 264–278. [doi: 10.1109/SP.2018.00025]
|
| [108] |
Bajaj S, Sion R. TrustedDB: A trusted hardware based database with privacy and data confidentiality. In: Proc. of the 2011 ACM SIGMOD Int’l Conf. on Management of Data. Athens: ACM, 2011. 205–216. [doi: 10.1145/1989323.1989346]
|
| [109] |
Bajaj S, Sion R. TrustedDB: A trusted hardware-based database with privacy and data confidentiality. IEEE Trans. on Knowledge and Data Engineering, 2014, 26(3): 752-765.
[doi:10.1109/TKDE.2013.38] |
| [110] |
Arasu A, Blanas S, Eguro K, Joglekar M, Kaushik R, Kossmann D, Ramamurthy R, Upadhyaya P, Venkatesan R. Secure database-as-a-service with CipherBase. In: Proc. of the 2013 ACM SIGMOD Int’l Conf. on Management of Data. New York: ACM, 2013. 1033–1036. [doi: 10.1145/2463676.2467797]
|
| [111] |
Arasu A, Blanas S, Eguro K, Kaushik R, Kossmann D, Ramamurthy R, Venkatesan R. Orthogonal security with CipherBase. In: Proc. of the 6th Biennial Conf. on Innovative Data Systems Research. Asilomar, 2013.
|
| [112] |
Intel. Enclave memory measurement tool for Intel® software guard extensions (Intel® SGX) enclaves. 2019. https://www.intel.com/content/www/us/en/content-details/671037/enclave-memory-measurement-tool-for-intel-software-guard-extensions-intel-sgx-enclaves.html
|
| [113] |
El-Hindi M, Ziegler T, Heinrich M, Lutsch A, Zhao ZG, Binnig C. Benchmarking the second generation of Intel SGX hardware. In: Proc. of the 18th Int’l Workshop on Data Management on New Hardware. Philadelphia: ACM, 2022. 5. [doi: 10.1145/3533737.3535098]
|
| [114] |
Orenbach M, Lifshits P, Minkin M, Silberstein M. Eleos: Exitless OS services for SGX enclaves. In: Proc. of the 12th European Conf. on Computer Systems. Belgrade: ACM, 2017. 238–253. [doi: 10.1145/3064176.3064219]
|
| [115] |
SecGear. 2023. https://github.com/openeuler-mirror/secGear
|
| [116] |
Eskandarian S, Zaharia M. ObliDB: Oblivious query processing for secure databases. Proc. of the VLDB Endowment, 2019, 13(2): 169-183.
[doi:10.14778/3364324.3364331] |
| [117] |
Islam MS, Kuzu M, Kantarcioglu M. Access pattern disclosure on searchable encryption: Ramification, attack and mitigation. In: Proc. of the 19th Annual Network and Distributed System Security Symp. San Diego: The Internet Society, 2017.
|
| [118] |
Goldreich O. Towards a theory of software protection and simulation by oblivious RAMs. In: Proc. of the 19th Annual ACM Symp. on Theory of Computing. New York: ACM, 1987. 182–194. [doi: 10.1145/28395.28416]
|
| [119] |
Goldreich O, Ostrovsky R. Software protection and simulation on oblivious RAMs. Journal of the ACM, 1996, 43(3): 431-473.
[doi:10.1145/233551.233553] |
| [120] |
Stefanov E, Shi E, Song DX. Towards practical oblivious RAM. In: Proc. of the 19th Annual Network and Distributed System Security Symp. San Diego: The Internet Society, 2012.
|
| [121] |
Shi E, Chan THH, Stefanov E, Li MF. Oblivious RAM with O((LogN)3) worst-case cost. In: Proc. of the 17th Int’l Conf. on the Theory and Application of Cryptology and Information Security. Seoul: Springer, 2011. 197–214. [doi: 10.1007/978-3-642-25385-0_11]
|
| [122] |
Stefanov E, van Dijk M, Shi E, Fletcher C, Ren L, Yu XY, Devadas S. Path ORAM: An extremely simple oblivious RAM protocol. In: Proc. of the 2013 ACM SIGSAC Conf. on Computer & Communications Security. Berlin: ACM, 2013. 299–310. [doi: 10.1145/2508859.2516660]
|
| [123] |
Ren L, Fletcher CW, Kwon A, Stefanov E, Shi E, van Dijk M, Devadas S. Constants count: Practical improvements to oblivious RAM. In: Proc. of the 24th USENIX Security Symp. 2015. Washington: USENIX Association, 2015. 415–430.
|
| [124] |
Devadas S, van Dijk M, Fletcher CW, Ren L, Shi E, Wichs D. Onion ORAM: A constant bandwidth blowup oblivious RAM. In: Proc. of the 13th Theory of Cryptography Conf. Tel Aviv: Springer, 2016. 145–174. [doi: 10.1007/978-3-662-49099-0_6]
|
| [125] |
Li YP, Chen MH. Privacy preserving joins. In: Proc. of the 24th IEEE Int’l Conf. on Data Engineering. Cancun: IEEE, 2008. 1352–1354. [doi: 10.1109/ICDE.2008.4497553]
|
| [126] |
Arasu A, Kaushik R. Oblivious query processing. In: Proc. of the 17th Int’l Conf. on Database Theory. Athens: OpenProceedings.org, 2014. 26–37.
|
| [127] |
Krastnikov S, Kerschbaum F, Stebila D. Efficient oblivious database joins. Proc. of the VLDB Endowment, 2020, 13(12): 2132-2145.
[doi:10.14778/3407790.3407814] |
| [128] |
Chang Z, Xie D, Wang S, Li FF. Towards practical oblivious join. In: Proc. of the 2022 Int’l Conf. on Management of Data. Philadelphia: ACM, 2022. 803–817. [doi: 10.1145/3514221.3517868]
|
| [129] |
Chang Z, Xie D, Li FF, Phillips JM, Balasubramonian R. Efficient oblivious query processing for range and kNN queries. IEEE Trans. on Knowledge and Data Engineering, 2022, 34(12): 5741-5754.
[doi:10.1109/TKDE.2021.3060757] |
| [130] |
Hackenjos T, Hahn F, Kerschbaum F. SAGMA: Secure aggregation grouped by multiple attributes. In: Proc. of the 2020 ACM SIGMOD Int’l Conf. on Management of Data. Portland: ACM, 2020. 587–601. [doi: 10.1145/3318464.3380569]
|
| [131] |
Ren XL, Su L, Gu Z, Wang S, Li FF, Xie Y, Bian S, Li C, Zhang F. HEDA: Multi-attribute unbounded aggregation over homomorphically encrypted database. Proc. of the VLDB Endowment, 2022, 16(4): 601-614.
[doi:10.14778/3574245.3574248] |
| [132] |
Asharov G, Chan THH, Nayak K, Pass R, Ren L, Shi E. Locality-preserving oblivious RAM. In: Proc. of the 38th Annual Int’l Conf. on the Theory and Applications of Cryptographic Techniques. Darmstadt: Springer, 2019. 214–243. [doi: 10.1007/978-3-030-17656-3_8]
|
| [133] |
Chakraborti A, Aviv AJ, Choi SG, Mayberry T, Roche DS, Sion R. RORAM: Efficient range oram with O(log2 N) locality. In: Proc. of the 2019 Network and Distributed Systems Security (NDSS) Symp. 2019. San Diego: The Internet Society, 2019.
|
| [134] |
Zheng WT, Dave A, Beekman JG, Popa RA, Gonzalez JE, Stoica I. Opaque: An oblivious and encrypted distributed analytics platform. In: Proc. of the 14th USENIX Conf. on Networked Systems Design and Implementation. Boston: USENIX Association, 2017. 283–298. [doi: 10.5555/3154630.3154653]
|
| [47] |
田洪亮, 张勇, 李超, 邢春晓. 云环境下数据库机密性保护技术研究综述. 计算机学报, 2017, 40(10): 2245-2270.
[doi:10.11897/SP.J.1016.2017.02245] |
| [57] |
刘晋璐, 秦静, 汪青, 赵博, 张茜, 苏烨. 复杂语义可搜索加密研究. 密码学报, 2022, 9(1): 1-22.
[doi:10.13868/j.cnki.jcr.000500] |
 2024, Vol. 35
2024, Vol. 35


