2. 国防科技大学 系统工程学院, 湖南 长沙 410073;
3. 中国科学院 计算技术研究所, 北京 100190
2. College of Systems Engineering, National University of Defense Technology, Changsha 410073, China;
3. Institute of Computing Technology, Chinese Academy of Sciences, Beijing 100190, China
知识图谱的概念自2012年正式提出之后, 相关研究迅速成为热点研究, 并且通过几年发展, 知识图谱成为继自然语言处理之后人工智能领域的又一新兴研究方向[1,2]. 最初的知识图谱是Google为了改善搜索引擎, 提高搜索效率而提出的, 主要服务于搜索引擎中的智能问答. 但是随着多年的技术创新和应用场景的扩展, 知识图谱逐渐成为一种可以支撑多种领域应用、高效储存信息的数据形式. 知识图谱的规模越来越大, 能储存的知识越来越广泛, 逐步出现了各种领域知识图谱, 诸如: 通用知识图谱、医疗知识图谱、政务知识图谱等. 为更多的人工智能应用提供底层数据服务, 如: 推荐系统[3]、智能问答[4]等.
随着知识图谱逐步成为一个全新的研究方向, 针对其研究的划分越来越清晰, 研究内容越来越全面, 包含了知识抽取、图谱构建、知识表示、知识融合、知识推理、图谱补全、质量评估等[5,6]. 但是, 随着知识图谱的应用越来越广泛, 传统的静态知识图谱已经不能满足人们的需求[7], 缺少的动态变化是限制其的重要因素之一, 因此, 时序知识图谱的概念和相关研究就应运而生[8], 逐渐成为学界研究的热点. 而以时序知识图谱为核心的相关研究与应用受到工业界和学术界的广泛关注[9].
时序知识图谱在2016年才被提出[9], 相关研究还不足10年, 但是其与知识图谱紧密相关, 所以在研究初期就参考知识图谱有了详细的细分方向研究, 如: 时序知识抽取[10]、时序知识表示、时序知识推理等[1,9]. 其中, 时序知识表示和推理是最为核心和关键的研究方向, 也是发展至今研究进度最快的方向, 有较多的研究成果产出. 时序知识表示和推理, 在整个时序知识图谱研究中是最为重要的, 是一切其他研究的基础, 表示推理效果好坏在很大程度上决定其他方向的研究和时序图谱的应用效果. 因此, 本文针对现有的时序知识图谱表示与推理的研究进展和未来趋势进行介绍和分析, 以期望为后来的研究者提供参考, 帮助新关注此领域的研究者们更快地了解当前时序知识图谱的研究动态.
同时, 本文根据现有的所有表示推理模型, 归纳构建了一个时序知识图谱表示与推理模型理论框架, 并以此来介绍对比现有模型, 帮助后来的研究者更好地开发设计新的、更优秀的表示推理模型.
最后, 本文也结合当前的发展现状, 与实际面临的问题挑战, 提出了几个未来较为可行的时序图谱表示推理研究方向, 以期望为研究者提供一些灵感.
1 时序知识图谱的相关概念与定义2016年, Jiang等人[8]首次针对性的考虑时间信息对知识图谱的影响, 对此进行了初步研究, 并提出了时序知识图谱的概念(temporal knowledge graph, TKG). 通俗地讲, 时序知识图谱就是在传统知识图谱三元组的基础上增加了时间信息. 举个简单的例子, (冬奥会, 举办地, 北京, [2022年2月4日, 2022年2月20日])表示实体“冬奥会”与“北京”之间在2022年2月4日–2022年2月20日这个时间间隔内具有“举办地”这个关系. 而对于时序知识图谱的规范化的定义如下.
定义1 (时序知识图谱). 时序知识图谱定义为带有时间戳的有向图
时序知识图谱推理相较于传统的静态知识图谱推理, 多了时间信息, 因此推理类型有所扩展. 在原有的主语(宾语)实体预测、关系预测的基础上增加了时间预测和未来预测. 针对时序知识图谱
定义2 (实体预测). 对于时序知识图谱
定义3 (关系预测). 对于时序知识图谱
定义4 (时间预测). 对于时序知识图谱
定义5 (未来事件预测). 对于时序知识图谱
未来事件预测与实体预测的区别在于待预测四元组中的时间信息是否在知识图谱中出现过, 如果预测四元组事件发生在未来(即时间信息不在原知识图谱中), 就是未来事件预测.
2 时序知识图谱表示与推理模型理论框架归纳相较于静态知识图谱, 时序知识图谱中的时间信息发挥重大作用, 而时间信息本身很难直接对其特征进行描述, 因此研究者们更多的是关注时间信息对实体或关系带来的影响, 其中最具代表性的手段就是通过对实体、关系的历史信息提取来获取时间信息的影响. 因此, 现有较多的时序知识图谱表示模型对于时间信息的处理采用对于历史信息的提取和对其特征的挖掘. 往往对于历史信息更高效的挖掘可以带来更大的预测效益.
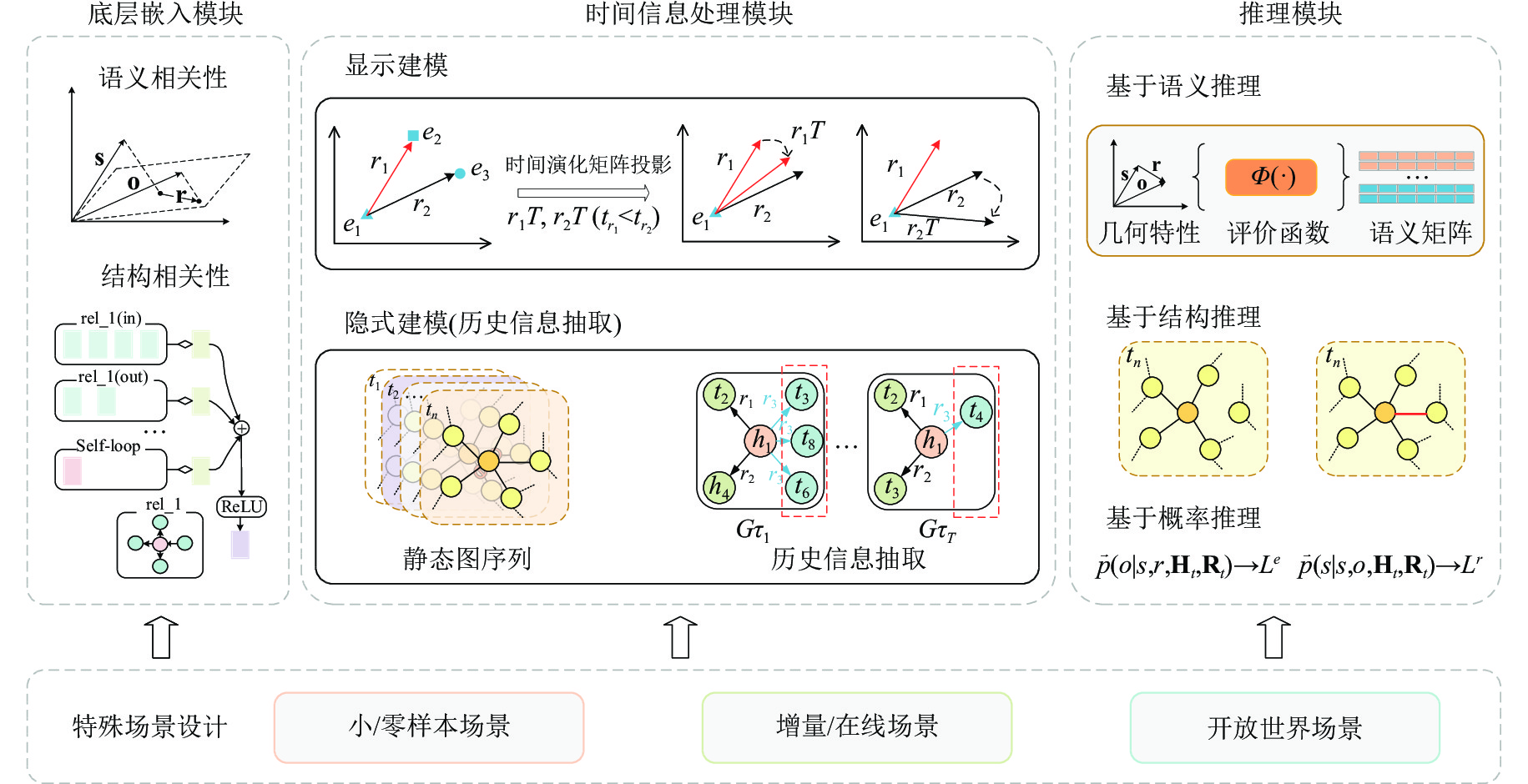
本文根据时序知识图谱的特殊性和应用场景, 归纳出了一个适用于所有时序知识图谱表示与推理模型的通用理论框架, 如图1所示. 在此框架中, 将表示与推理模型分为3个核心模块和一个特殊设计: 底层嵌入模块、时间信息处理模块、推理模块和特殊场景定制设计. 3个模块和一个设计是一个时序知识图谱表示与推理模型中最为核心的4个部分. 其中底层嵌入模块是整个模型的底座, 不同的嵌入方法选择将很大程度的影响后续各模块的设计与模型最终的表示与推理能力; 时间信息处理模块是模型处理时序信息的重要环节, 其通过不同方法从时序图谱中捕获知识在时间线上的变化规律; 推理模块是模型对接应用的重要出口, 根据不同的任务选择合适的推理方法会提升模型整体性能; 特殊场景定制设计, 对模型进行了进一步的个性化限制, 使得模型在不同场景和任务中具备更好的表现. 4个部分相互独立又彼此支撑, 共同作用下形成一个高效的时序知识图谱表示与推理模型. 下面逐一对其进行更详细介绍.
|
图 1 时序知识图谱表示与推理模型的通用理论框架 |
2.1 底层嵌入模块
底层嵌入是整个表示推理模型的基础, 是模型的底层基石, 底层嵌入的不同设计决定了后续实体关系表示的不同效果和特性. 本文分析时序图谱的特殊性, 将底层嵌入中的具有特殊设计的方法分两个大类, 一为基于语义相关性构建的嵌入, 二为基于结构相关性构建的嵌入. 其他的方法则是在底层嵌入中, 没有针对性的特殊设计, 也可以说这类模型没有底层嵌入, 而是在后续时间信息处理模块的设计中, 通过针对性设计兼顾时间信息处理的同时生成实体和关系的嵌入表示.
• 基于语义相关性构建, 是指时序知识图谱表示模型底层嵌入是基于图谱实体关系间的语义相关性进行构建的. 语义相关性体现为图谱中知识(实体-关系-实体)蕴含的语义联系, 实体、关系的嵌入同样保持着此种联系. 底层嵌入不包含时间信息, 因此就是针对时序中的每个时刻的静态知识图谱进行建模. 基于语义相关性构建的底层嵌有TransE[11]、SimplEx[12]、DisMult[13]、RotatE[14]等. 时序模型基于这些静态表示方法对实体和关系进行底层嵌入, 并在此基础上进行特殊设计, 随后再添加不同的针对时间信息的处理手段.
• 基于结构相关性构建, 是指时序知识图谱表示模型底层嵌入是基于图谱实体关系间的语义相关性进行构建的. 结构相关性体现为图谱中的图结构特性, 实体节点与邻居节点通过代表关系的边进行连接. 底层嵌入通过图结构信息进行特征提取, 实现对实体、关系的建模. 这类方法通常采用GCN[15]或RGCN[16]来对图谱中的结构信息进行提取并生成实体和关系的底层嵌入.
2.2 时间信息处理模块时间信息是时序图谱的重要特征之一, 是区别于静态知识图谱的关键要素. 而历史信息是时间信息的一种显示表征, 蕴含了实体、关系和知识随着时间演变而产生的动态变化特征. 因此模型对历史信息的特征挖掘和利用效率可以决定时序图谱表示的准确性和后续推理的精度. 本文将现有模型对于时间信息的处理方式进行归纳, 将时间信息处理模块采用的方法分为两类, 时间信息显式建模方法和时间信息隐式建模(历史信息抽取)方法.
• 显式建模方法, 是模型通过对时间信息的特殊处理, 学习时间对实体、关系产生的影响. 此类方法, 直接从时间信息的处理中, 捕获实体、关系、知识等在不同时间下的改变. 此类方法的代表, 就是基于静态图谱表示方法时序改造的模型, 其在原有表示的基础上对时间信息对其的影响进行建模.
• 历史信息抽取方法, 是对实体或知识的历史信息直接进行提取并捕获其对实体、关系的影响. 其中具有代表性的方法是, 通过RNN、LSTM等对图谱序列进行历史信息的提取或通过霍克斯点过程[17,18]对历史信息的影响进行建模.
2.3 推理模块推理既是评价表示效果的重要参考, 亦是时序图谱的下游任务之一, 因此推理模块构建是模型中不可缺少的一部分. 与此同时, 推理模块的构建方法选择不同, 往往模型的评价函数、损失函数等均有所差异. 本文根据推理依据的差异性, 将模型的推理模块分为4大类: 基于语义推理、基于结构推理、基于概率计算推理和混合推理.
• 基于语义推理, 是模型根据实体、关系的语义关系构建评价函数进行推理, 其中常见的有基于翻译的评价函数[11,19–21]、双线性函数[22]等.
• 基于结构推理, 是模型根据图谱的结构特征构建相应的评价函数, 更多的是依赖图谱的图特性, 常见的方法有强化学习[23–25]、路径推理[26,27]等.
• 基于概率计算推理, 是模型将推理转换为条件概率计算问题.
• 混合推理, 则是模型同时利用语义信息和结构信息构建评价函数, 进行联合推理.
2.4 特殊场景定制设计特殊场景的定制设计, 在实际模型设计时, 是首要考虑的因素, 需要在模型的设计之初就明确知道该模型将适用何种场景, 是否需要对特殊场景进行针对性的定制化设计. 模型针对特殊的应用场景, 需要针对性的设计和调整模型框架和思路. 现阶段的模型, 通过归纳, 暂时有如下3种特殊场景, 分别是增量/在线场景[28–30]、小/零样本场景[31–33]和开放世界场景[34–36].
• 增量/在线场景, 是指在对模型更新训练过程中仅采用新增或更新的数据和少量原始数据对模型进行针对性的训练. 时序知识图谱在现实应用中有极强的即时性, 随着时间的变化, 知识更新速度较快, 为此选用增量式的训练方法会极大减少计算资源和时间消耗.
• 小/零样本场景, 是指训练集样本数量少或没有的特殊场景. 时序知识图谱在特殊领域应用时, 诸如: 医疗图谱、军事图谱等, 往往面临着训练数据稀疏或缺失的情况. 针对此场景, 小/零样本模型的开发就帮助摆脱困境.
• 开放世界场景, 是指图谱应用时, 有新的实体和关系出现, 模型支持对新实体进行推理预测. 现实应用时, 往往会出现不在原有图谱中的新实体, 针对这类新实体, 普通的表示推理方法无法生成表示并准确推理, 为此针对性的开发定制模型至关重要.
3 现有时序表示推理模型分析时序知识图谱相关概念的提出距今尚不足10年, 但是相关研究工作已经较为全面, 尤其是表示推理方面的研究取得了良好效果. 具有代表性的表示推理模型已有30余种, 各具特色, 且为后续工作带来了启发. 按照第2节介绍的表示推理模型理论, 现有所有表示推理模型的均可以按照上述模块进行拆解. 因此本节将根据各个模块, 对所属模型进行详细对比分析. 首先对各模型在3个模块一个设计中使用方法的类别进行了归纳, 详细如表1所示.
| 表 1 时序表示推理模型一览表 |
3.1 底层嵌入模块
底层嵌入是模型的基石, 它的选择极大影响着后续的各个设计阶段. 由表1可以发现最初几年的模型大部分以基于语义相关性构建的静态图谱表示作为底层嵌入, 研究者在此类传统静态图谱表示的基础上进行拓展, 在原有实体、关系的基础上增加时间变量, 着重挖掘时间对实体、关系的影响. 2021年后, 研究者们逐渐采用基于结构相关性构建的底层嵌入替代语义相关性, 更多开始采用图卷积网络对实体、关系进行底层嵌入建模, 此类方法, 可以很好地捕获图谱的图结构信息, 能聚合邻居节点间的信息. 与此同时, 不采用底层嵌入的模型也越来越多, 这类模型在针对实体关系建模时不采用静态图谱表示作为底层嵌入, 直接随机初始化嵌入, 虽然不具备时序图谱的信息, 但是却具有更强的后续可塑性, 依赖后续的处理依然可以发挥出良好的效果. 下面对两类底层嵌入方法所属具有代表性的模型进行详细介绍.
(1)基于语义相关性
Jiang等人2016年提出了第1个针对时序知识进行编码表示模型t-TransE[8], 其在传统静态模型TransE构建三元组的基础上增加了时间约束信息, 形成了最早的时序知识表示方法四元组
t-TransE模型的底层嵌入可以同样选择TransE系列的进化模型TransH和TransR等. 由于对于关系的演化过程进行了建模以及利用时间一致性信息进行了约束, t-TransE模型在实体预测、链接预测等问题上的性能均优于传统的静态表示方法. 自此t-TransE模型为时序知识图谱的研究打开了一扇大门, 越来越多的工作开始聚焦于时序知识图谱的表示学习, 并不断提出更具有效果的时序表示模型.
作为最早关注时序知识图谱相关研究的团队, Jiang等人在提出了第1个应用于时序知识图谱表示模型t-TransE的同年, 针对时序知识图谱的推理和补全进行了研究, 提出了一种时间感知的知识图谱补全模型TransE-TAE[37]. 为了适用于时序知识图谱的表示和补全, 其在传统静态知识图谱表示TransE的基础上对关系向量增加了时间信息对其的影响. TransE-TAE适用于时序图谱补全任务, 即实体预测和关系预测, 是最早的适用于时序知识图谱推理补全的模型, 同时也被作为此类任务的基线模型.
2018年, Leblay等人同样在原有静态知识图谱表示方法TransE的基础上增加了时间信息的约束, 采用3种方法来修改原三元组评价函数使其可以表示时间信息对三元组的影响, 提出了模型X-TransE[39], 其是首个可以对时序图谱中的时间要素进行预测的模型, 即针对三元组知识预测其所生效的时间段.
同年, 发表在自然语言处理顶会EMNLP上的两篇工作, 同样采用了TransE作为底层嵌入. 其中Dasgupta等人参考了TransH的改进思路设计了模型HyTE[41], 相比于t-TransE其对时间信息的利用更为有效; 而García-Durán等人则仅是利用静态表示来初始化实体关系表示, 选择用LSTM来捕获时间信息, 提出了TA-TransE/TA-DistMult[40], 两者基于不同的静态图谱表示方法进行底层嵌入, 效果有所差异, TA-TransE受限于基础静态表示模型的劣势, 在表示效果上要远逊色于TA-DistMult.
2020年是时序知识图谱表示推理模型研究成果微微爆发的一年, 这一年有较多的模型涌现, 国内外研究者不仅局限于选择TransE作为底层嵌入, 而是将视线转移到了其他表现优异的静态表示模型上.
Goel等人提出了模型DE-SimplE[42], 将实体、时间信息作为输入信息以得到实体在任何时间戳下的嵌入表示. 该模型底层嵌入可以选择静态表示模型TransE、DistMult、SimplE等, 通过Goel等人的实验对比, 选择SimplE形成DE-SimplE的模型表现最佳.
在此之后, Lacroix等人在静态知识图谱表示模型ComplEx的基础上增加时间约束, 将原有的三元组表示拓展为四维张量, 提出了模型TComplEx/TNTComplEx[45]. 该模型较DE-SimplE在效果上有了细小提升.
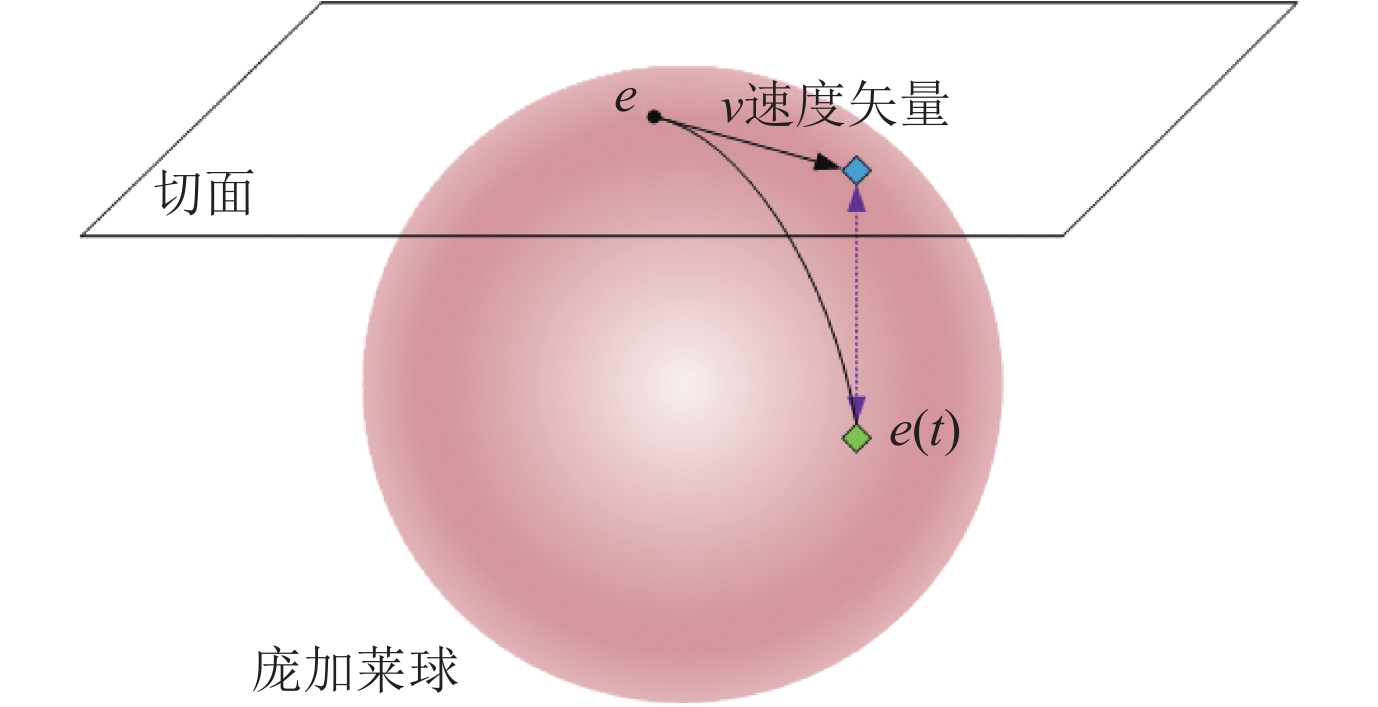
随后, Jain等人[47]和Han等人[48]分别选择静态表示中复数空间模型ComplEx与黎曼流形模型[67]作为底层嵌入, 提出了模型TIMEPLEX[47]和DyERNIE[48]. 其中TIMEPLEX方法将实体、关系和时间嵌入到复数空间, 将时间差异作为显式特征, 使学习到的嵌入能够捕获关系之间的隐式时间关系. 另外, 其使用高斯分布建模复发关系的固定循环周期以及特定实体关系之间的时间差异. 而DyERNIE为如图2所示的非欧几里得嵌入方法, 学习黎曼流形乘积中的演化实体表示, 其中组合空间是从基础数据的截面曲率估计的. 流形能够更好地覆盖时序图谱上的各种几何结构. 且DyERNIE为了捕获时序图谱的演化动态, 让实体表示根据在每个时间戳的切线空间中定义的速度向量进行演化.
|
图 2 DyERNIE的非欧几里得嵌入 |
同年, 国内田满鑫等人[44]同样是以TransE模型为基础, 在其上增加了时间对三元组的约束. 其思路与HyTE模型的思路类似, 但是针对其不能区分时间对不同实体造成影响的差异, 以TransE模型为基础, 根据应用场景时间粒度的差异构建了一个时间转移矩阵, 使得同一时间下对于不同类型实体, 通过转移矩阵能够产生不同程度的状态变化, 可以区分同一时间对不同类型实体的影响.
最近3年, 采用静态图谱表示底层嵌入的模型逐渐减少, 2021年Sadeghian等人受静态表示RotatE的启发, 提出了ChronoR[51]模型, 将关系和时间信息建模为正交矩阵的一部分, 对主语实体进行基于关系和时间信息的旋转变换之后, 它就会落在其对应的宾语实体附近. ChronoR是一种旋转模型的方法, 因此其可以建模逆反关系、复合关系和对称关系.
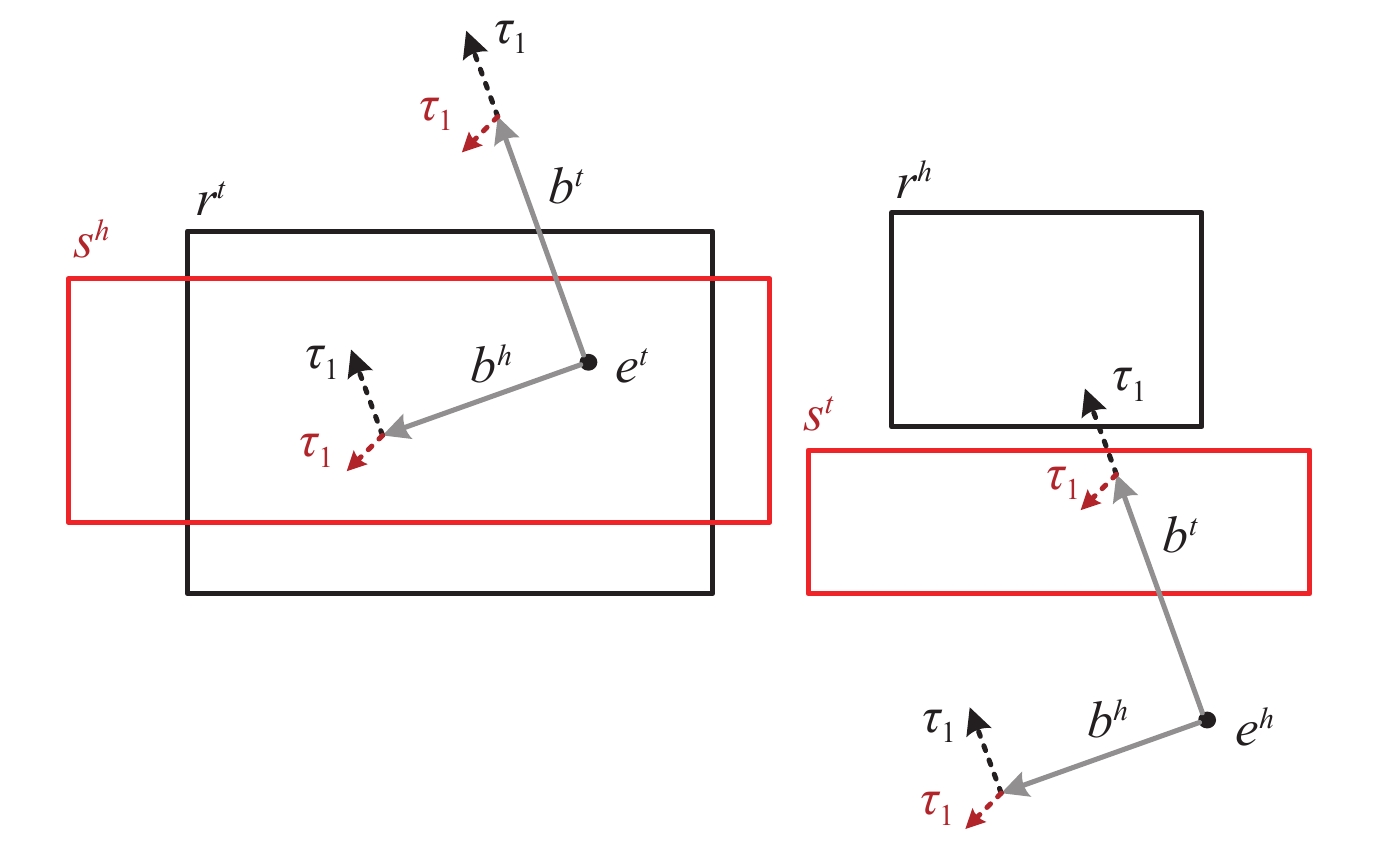
2022年Messner等人在静态知识图谱表示BoxE的基础上设计了适用于时序知识图谱表示的盒子嵌入模型BoxTE[59]. 静态表示模型BoxE[68]与其他表示模型在关系表示上具有极大的差异, 它不仅用一个向量来对关系进行表示, 反而是将关系表示为空间中的一个矩形区域, 即为一个盒子(box). 而基于此方法, 在其基础上加上时间信息, 就演变为了适用于时序图谱表示的BoxTE, 如图3所示. 它延续了BoxE表达能力强、捕获隐式推理规则的优势. Johannes等人着重对推理规则进行了研究, BoxTE具备极强的推理规则的归纳能力, 可以捕获多种时间推理模式特征, 诸如针对跨时间推理模式等.
|
图 3 BoxTE的特殊盒子结构图 |
(2)基于结构相关性
知识图谱是一种特殊的图结构, 因此适用图的表示方法也可以迁移到知识图谱中, 2018年Schlichtkrull联合GCN的作者Kipf一同提出了针对知识图谱的表示学习模型R-GCN[16], 在GCN的基础上增加了对知识图谱中多种关系的建模. 因此, 在时序知识图谱中, 以图卷积作为底层嵌入表示成为部分研究者的首选, 其可在最初始阶段就捕获图谱的结构的信息, 为后续的表示奠定了良好基础.
2020年, 发表在顶会EMNLP上的两篇文章首先采用了图卷积作为底层嵌入. 其中Jin等人定义了一个相似于RNN的表示模型RE-Net[46], 其针对每个时间戳上的静态图谱使用R-GCN作为底层嵌入聚合实体的邻域信息, 并使用基于RNN的事件编码器对事件序列进行建模捕获实体受时间信息影响的特征.
而Wu等人针对时序知识表示与推理中时间异构性(包含实体发生的多变性与稀疏性)带来的表示困难与预测精度降低的问题, 设计了一种结合神经信息传递和时序动态信息的模型TeMP[49]. 在模型中, 使用频率门控和数据填补技术来克服时间异构性带来的负面影响. 其中实体发生的稀疏性具体表现为在每个时间点下, 仅有少量实体活动, 大部分实体处于静态状态, 且在相当长的一段时间内, 大部分实体均保持静止, 且结构性的表示方法仅对活动实体周边关联的实体表示进更新, 这使得大部分实体表示在多个时间步长内共享陈旧的表示, 这将极大影响实体表示的准确性. 为此, Wu等人通过数据填补的方法将非活动实体的历史中上一个活动时刻的表示添加到对当前时刻表示的更新中. 这个策略参考了时序图表示中历时性表示的方法, 利用过去时刻的表示对当前时刻的表示进行轻度干预, 使实体表示实现随着时间变化的动态演变. 针对每个静态的知识图谱采用R-GCN对实体、关系的表示进行嵌入.
因为R-GCN对于图谱结构特征挖掘具备极佳优势, 最近3年均有基于此构建的表示推理模型.
2021年开年, Zhu等人在RE-Net的基础上改进了对历史信息的处理方式, 提出了时序复制生成网络模型CyGNet[52], 其同样是采用R-GCN对实体关系进行底层嵌入.
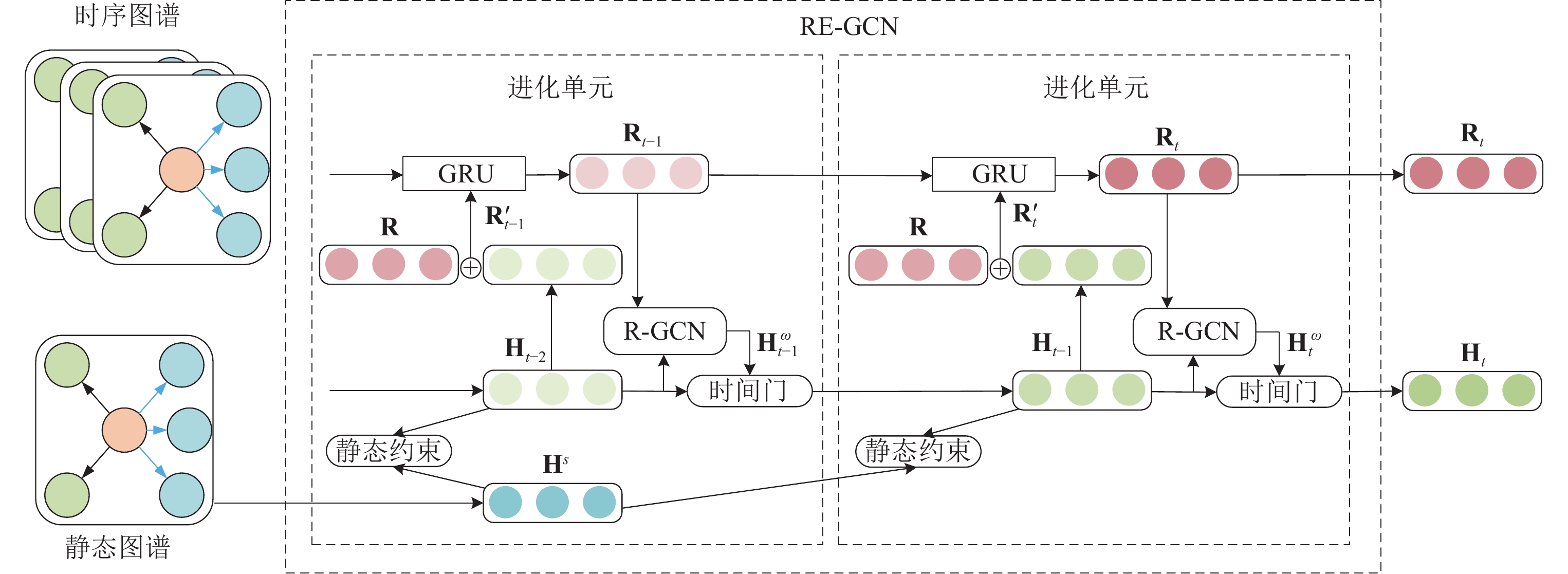
随后, Li等人同样是受到RE-Net模型的启发提出了模型RE-GCN[54], 依然是基于时间线上静态图谱序列对实体和关系进行建模, 同时着重考虑历史信息对当前事实的影响. 为此依托GCN捕获图谱结构信息特征, 设计了如图4所示的进化单元来对实体历史信息对当前的影响进行建模, 同时还利用实体静态属性(常识知识)来对实体表示进行约束.
|
图 4 RE-GCN的进化单元结构图 |
同年, Li等人又参考人类推理的双过程理论, 将推理分为两个阶段: 一是线索搜索(历史信息捕获), 二是时间推理. 并基于RGCN和强化学习提出了用于时序知识图谱的聚类预测算法CluSTeR[56].
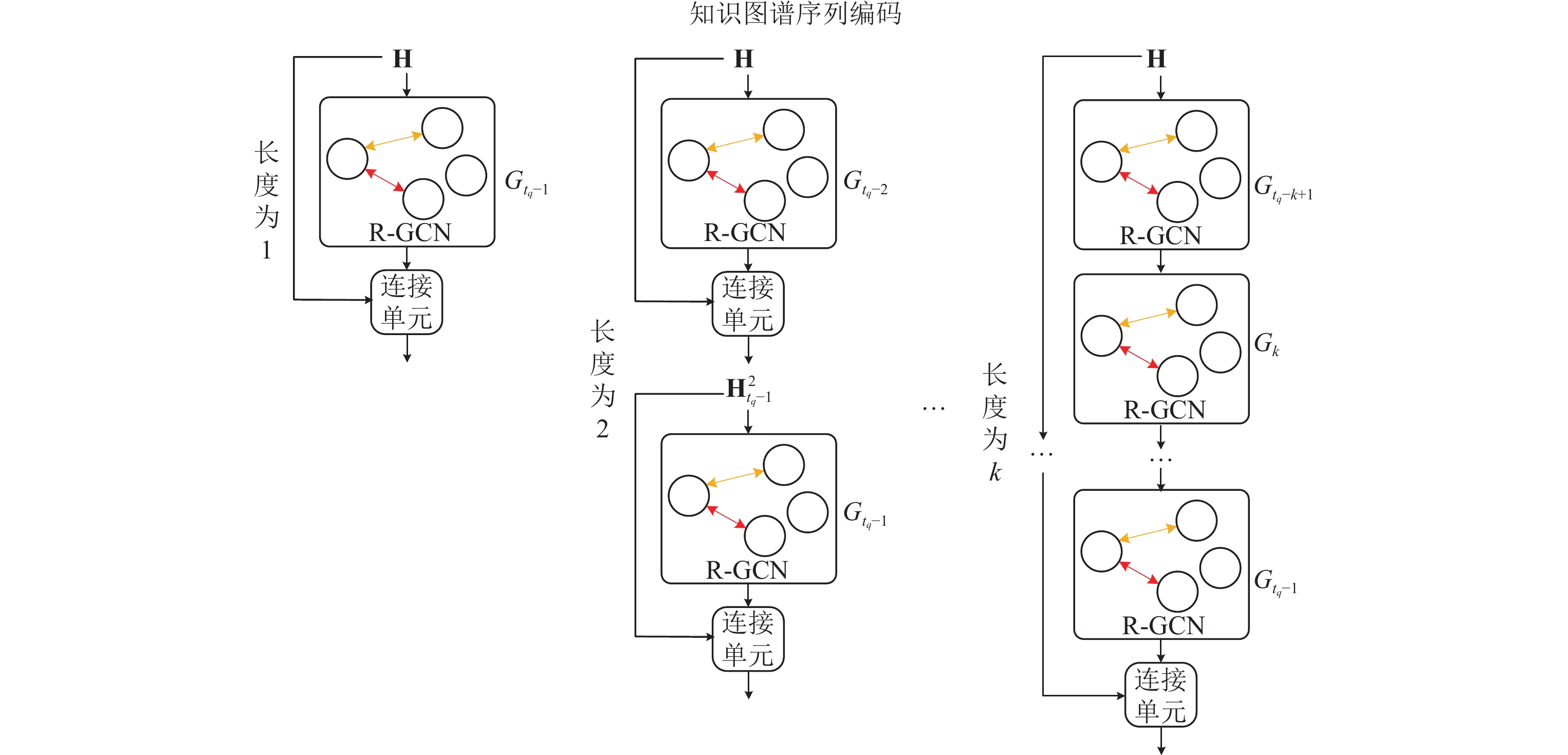
2022年同样有两篇工作选择图卷积作为底层嵌入, 第1篇是Park等人设计的一种新的方法EvoKG[58], 其将时序图谱的未来预测问题转化为两个核心子问题事件时间建模与网络结构演变, 并联合解决两个核心关键子问题. 而其通过分析在此之前的算法发现, 原有算法仅针对其中一个问题进行针对性的解决. 其中, EvoKG采用R-GCN作为底层嵌入对图结构进行建模, 并用RNN对时间序列进行建模. 第2篇是Li等人针对现有模型无法针对性对推理时的不同步长和差异性对不同知识的时间多样性进行建模的问题, 提出的CEN (complex evolutional network)模型[60], 在时间序列上预测知识图谱的推理过程, 并且通过在线学习, 实现了实时对知识图谱推理过程的提取. CEN模型包含1个KG序列编码器和1个演化表征解码器. KG序列编码器(如图5)利用RGCN针对每个图谱序列上的静态图谱进行初步建模, 将不同长度的最新历史KG序列编码为相应的实体进化表示. 然后, 演化表征解码器根据这些表征计算出所有实体的查询分数. 在演化表征解码器中, 由于多个演化表征包含多种长度的演化模式, 为了区分长度不同的进化模式的影响, CEN设计了1个长度感知的CNN, 它使用
|
图 5 CEN的知识图谱序列编码 |
2023年, Zhang等人提出的模型HGLS[66], 通过设计的层次化的关系型图神经网络HRGNN, 来编码全局图结构. 其中, 子图层级, 就是针对同一时间戳下的静态图谱使用RGCN进行建模; 全图层级, 将时间影响转换为边权重, 然后采用注意力机制建模实体的全图特征.
上述方法均采用图卷积作为底层嵌入, 且后续处理手段各不相同, 这体现了图卷积底层嵌入的泛化性与对图结构特征挖掘的优越性. 由此可以预见, 在未来几年内, 其依然会是一个不错的底层嵌入方法.
(3)对比分析
对比两类底层嵌入参考表2可以发现, 基于语义相关性构建的底层嵌入在早期几年的模型中使用广泛, 但是随着几年发展, 使用此类底层嵌入的模型越来越少, 究其原因是因为这类底层嵌入在设计之初就为了追求更高表示效率, 模型设计巧妙, 但是可拓展和改进空间较小, 后续增加时间信息处理模块后往往能取得不错的效果, 但是随着时序图谱表示推理模型的整体进步, 不错的效果已经不能满足当前的需求. 因此, 这类底层嵌入就不再是研究者构建模型的主要选择.
| 表 2 底层嵌入方法对比分析表 |
基于结构相关性构建的底层嵌入由于其着重于图结构信息的挖掘, 后续增加了时间信息处理模块后, 在一定程度上从语义层面对实体关系的表示进行了增强. 使得此类方法在当前依然能保持极高的使用率, 其次基于结构性相关性进行建模在模型推理时有较好的可解释性.
同样由表1不难发现, 不进行底层嵌入的模型设计方案近年来越来越多, 研究者们更愿意摆脱静态知识图谱表示的影响, 全新的去构建一个适用于时序知识图谱的表示推理模型.
3.2 时间信息处理模块时间信息处理是既底层嵌入之后的第2个部分, 是时序图谱表示推理模型中最为重要的模块, 用来针对时间信息进行处理和利用, 此模块往往决定了表示和推理的效果. 下面针对此模块中时间信息显式建模与隐式建模两种方法下的典型模型进行详细介绍.
(1)显式建模方法
时间信息显式建模方法是对时间进行直接处理, 它不对实体关系的历史信息进行提取, 而是直接关注时间对于实体或关系的影响. 由表1可以发现, 对历史信息的隐式应用与底层嵌入阶段的静态图谱表示往往是对应的, 也就是说几乎所有的针对基于语义相关性构建的传统静态图谱表示进行时序拓展的模型都是在原有的基础上直接增加了对时间信息的处理, 不再提取历史信息并对其进行进一步处理. 下面针对时间显式建模方法中具有特色的手段进行介绍.
时序图谱表示的开山之作t-TransE[8], 使用转移矩阵(演化矩阵)
| $ g({r_i}, {r_j}) = ||{{\mathbf{r}}_i}{\mathbf{M}} - {{\mathbf{r}}_j}|{|_1}. $ |
t-TransE模型在对时序关系对进行建模的基础上, 考虑了3种时间一致性信息. 1)时序不相关性, 任何两个具有相同一对一关系以及同主语实体的事实的时间间隔是不能重叠的, 例如一个人在一段时间内只能是另一个人的配偶. 2)关系时间顺序, 对于某些具有时间顺序的关系, 一个事实三元组总会先于另一个事实三元组发生, 例如一个人出生于某地肯定是发生在他毕业于某学校之前. 3)时间范围性, 有些事实仅在特定时间段内是正确的, 超出范围该时间范围则无效.
而Jiang等人同年针对时序知识图谱补全而设计的模型TransE-TAE[37], 是在传统静态知识图谱表示TransE的基础上对关系向量增加了时间信息对其的影响. 具体体现在原有向量空间中关系向量的旋转, 如图6所示.

|
图 6 时间信息在TransE上的体现 |
同时TransE-TAE针对时间使用与t-TransE一样的一致性约束.
2018年, Leblay等人提出的X-TransE[39], 也是在TransE的基础上进行拓展, 其采用3种方法来修改原三元组评价函数使其可以表示时间信息对三元组的影响, 第1种是将时间信息与关系合并, 让每个在不同时间产生的关系形成一个新的三元组元素
| $ f(s, r:\tau , o) = - ||{\mathbf{s}} + {\mathbf{r:\tau }} - {\mathbf{o}}|| .$ |
第2种是将时间信息作为三元组的第4个元素, 同实体与关系一样, 通过评价函数训练获得时间信息的嵌入表示, 其评价函数则被改造为:
| $ {f_\tau }(s, r, o) = - ||{\mathbf{s}} + {\mathbf{r}} + {\mathbf{\tau }} - {\mathbf{o}}|| .$ |
第3种方法与第2种类似, 将时间信息表示为取值为[0, 1]的权重值, 其仅对主语实体和关系产生影响, 评价函数为:
| $ f(s, r, o, \tau ) = - ||{\mathbf{\tau }} \times ({\mathbf{s}} + {\mathbf{r}}) - {\mathbf{o}}|| .$ |
X-TransE通过上述方法, 对时序图谱中的时间进行预测, 即针对三元组知识预测其所生效的时间段. X-TransE虽然通过上述3种方式对时间信息进行了利用, 但是实际上对时间信息造成影响的特征挖掘能力较弱, 关系-时间合并的方法无法对连续时间点的关系进行有效区分, 增加关系类别数量导致标注样本稀疏; 直接对时间信息进行编码不足以获得时间的有效特征. 该方法是对时序信息较为简单的一种应用, 但是却是针对时间预测的一种最为基础和经典的方法.
同年, Dasgupta等人提出的模型HyTE[41]在TransE基础上的改造思路参考了TransH[19], 构建了时间超平面, 将实体和关系投影到相应的时间超平面上, 表示为:
| $\left\{ \begin{gathered} {P_\tau }({\mathbf{s}}) = {\mathbf{s}} - ({\mathbf{w}}_\tau ^{\rm{T}}{\mathbf{s}}){{\mathbf{w}}_\tau } \\ {P_\tau }({\mathbf{o}}) = {\mathbf{o}} - ({\mathbf{w}}_\tau ^{\rm{T}}{\mathbf{o}}){{\mathbf{w}}_\tau } \\ {P_\tau }({\mathbf{r}}) = {\mathbf{r}} - ({\mathbf{w}}_\tau ^{\rm{T}}{\mathbf{r}}){{\mathbf{w}}_\tau } \\ \end{gathered} \right. ,$ |
则其时序的评价函数为:
| $ {f_\tau }(s, r, o) = - ||{P_\tau }({\mathbf{s}}){\mathbf{ + }}{P_\tau }({\mathbf{r}}) - {P_\tau }({\mathbf{o}})|| .$ |
HyTE相比于t-TransE对时间信息的利用更为有效, 但由于同一时间段的三元组知识稀疏, 时间超平面导致无法充分挖掘多实体及关系的相关信息; 无法对时间对于不同实体造成的差异性进行区分. 导致时间信息利用的缺失.
2020年, Goel等人提出的DE-SimplE[42]直接将时间对实体表示的影响显式表达出来, 即实体
| $ {\textit{z}}_v^\tau [i] = \left\{ {\begin{array}{*{20}{l}} {{a_v}[i]\phi ({W_v}[i]\tau + {b_v}[i]),\;\; 1 \leqslant i \leqslant \gamma d} \\ {{a_v}[i], \qquad\qquad\qquad\quad \gamma d < i \leqslant d} \end{array}} \right. ,$ |
其中,
随后, Xu等人提出的ATiSE[43]定义的时间节点的显式表示方法是对时间的首次分类, 为了进一步挖掘时间信息对三元组影响的特征, 充分挖掘时间对实体演化的影响, 其将时间分为3种不同的类型趋势、周期和随机. 趋势即时间对于实体的影响可能是随着时间变化呈现线性变化的(多为衰减); 周期即时间对于实体的影响是成周期性变化的, 如: 奥运会4年开幕1次; 随机即时间对于实体的影响没有规律性.
| $ {\textit{z}}_v^\tau = {{\textit{z}}_v} + {\alpha _v}{w_v}\tau + {\beta _v}\sin (2\text{π} {\omega _v}\tau ) + N\left(0, \Sigma_v \right), $ |
其中,
基于静态知识图谱表示模型ComplEx进行拓展的TComplEx/TNTComplEx[45], 将原有的三元组表示拓展为四维张量, 并且在训练过程中保证时间对三元组中3个元素影响的一致性, 即:
| $ \left\langle {{s_i}, {r_j}, {{\bar o}_k}, {\tau _l}} \right\rangle = \left\langle {{s_i} \odot {\tau _l}, {r_j}, {{\bar o}_k}} \right\rangle = \left\langle {{s_i}, {r_j} \odot {\tau _l}, {{\bar o}_k}} \right\rangle = \left\langle {{s_i}, {r_j}, {{\bar o}_k} \odot {\tau _l}} \right\rangle .$ |
TComplEx对所有的实体和关系都增加了时间的约束, 但是在实际情况中, 部分实体和关系是具有时间不变性的, 即实体和关系是不随时间变化而发生改变的, 因此, Timothee等人[45]又将这些实体与关系的表示与其他实体关系进行了区分, 提出了TNTComplEx模型, 其保证了时间不对这类实体关系造成额外影响. TNTComplEx在时序知识图谱上的表现要优于TComplEx, 但是两个模型在时间尺度较大的Yago数据集上并没有特殊优势, 效果一般.
2021年, Sadeghian等人提出的ChronoR[51], 将关系和时间信息建模为正交矩阵的一部分, 对主语实体进行基于关系和时间信息的旋转变换之后, 它就会落在其对应的宾语实体附近, 具体表示如下:
| $\left\{ \begin{gathered} {Q_{r, \tau }}({\mathbf{s}}) = {\mathbf{o}} \\ {Q_{r, \tau }} = {[{\mathbf{r}}\mid{\mathbf{\tau }}]^4} \\ \end{gathered} \right. ,$ |
其中,
| $ \left\{\begin{gathered} \langle {\mathbf{A}}, {\mathbf{B}}\rangle : = {\rm tr} \left( {{\mathbf{A}}{{\mathbf{B}}^{\text{T}}}} \right) \\ \cos (\theta ): = \frac{{\langle {\mathbf{A}}, {\mathbf{B}}\rangle }}{{\sqrt {\langle {\mathbf{A}}, {\mathbf{A}}\rangle \langle {\mathbf{B}}, {\mathbf{B}}\rangle } }} \\ g(s, r, o, \tau ): = \left\langle {{Q_{r, \tau }}({\mathbf{s}}), {\mathbf{o}}} \right\rangle \\ \end{gathered} \right. .$ |
因此, ChronoR希望主语实体进行基于关系和时间信息的旋转变换之后, 与宾语实体的夹角的余弦值更大, 也就是夹角更小. ChronoR模型不仅继承了旋转模型能够建模多种关系模式的优势, 也将时间信息编码到实体的旋转过程中, 捕获了实体和关系的动态演化.
ChronoR是一种旋转模型的方法, 因此其可以建模逆反关系、复合关系和对称关系, 但是对于同一实体, 只能利用其一跳邻居进行表示学习和推理, 缺少了对知识图谱中多跳路径信息的捕获.
2022年, Zhang等人针对原有表示方法忽略了知识语义信息与时间信息的独立性, 提出的一种时间线溯源时序图谱表示方法TLT-KGE[62]. 区别于其他的表示方法, 其选择了在图7所示的复数空间对实体关系进行嵌入表示, 并对于实体关系的语义信息与时间信息分别在实数轴和复数轴上进行独立的建模.
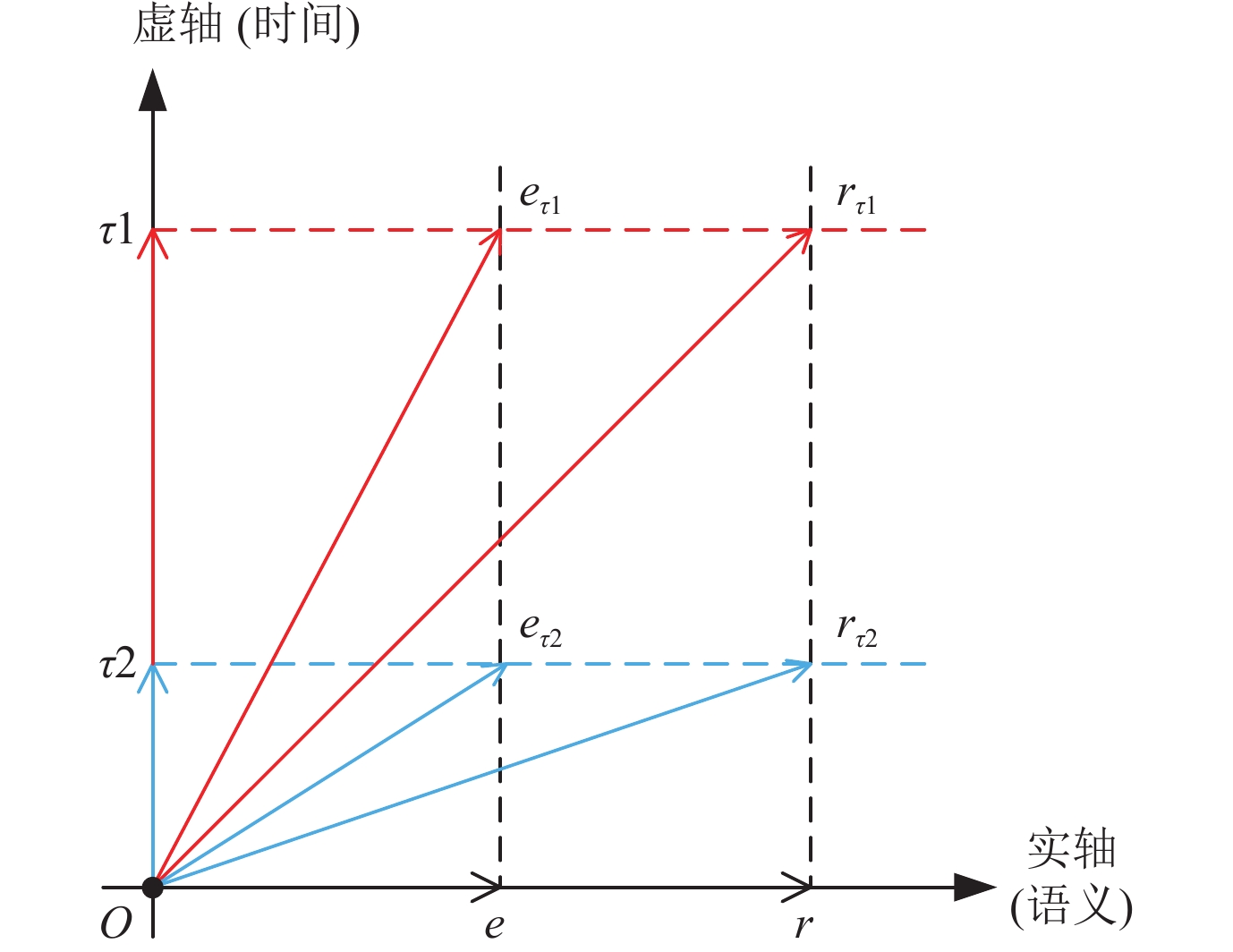
|
图 7 TLT-KGE中的复数空间 |
| $ {\mathbf{e}}_{s, \tau }^c = {{\mathbf{e}}_s} + {\mathbf{t}}_\tau ^ei{{, }}\;{\mathbf{e}}_{o, \tau }^c = {{\mathbf{e}}_o} + {\mathbf{t}}_\tau ^ei{{, }}\;{\mathbf{r}}_{r, \tau }^c = {{\mathbf{r}}_r} + {\mathbf{t}}_\tau ^ri{{, }} $ |
其中,
同时, Zhang等人[62]设计了两种组件共享时间窗口(STW)与关系时间戳组合(RTC), 分别用以增强实体表示和关系表示. 其中, 共享时间窗口旨在描述实体在相近时间段间的联系; 关系时间戳组合用以增强关系和时间信息之间联系, 提高关系对于时间的敏感度, 以此增强关系在不同时间下的表示能力.
2023年, Zhang等人提出的HGLS[66]设计了长短期表征提取模块, 用以捕获时间对实体和关系的影响. 它对短期和长期影响分别进行建模, 关系的语义在长期变化中趋于稳定, 因此用关系的静态表示作为其长期表示; HGLS使用GRU捕获实体关系的短期变化.
上述对当前使用时间信息显式建模方法的模型进行了介绍, 可以发现这类模型更多的是对时间的直接处理, 与底层嵌入表示紧密联系, 往往在原有参考的静态图谱表示的基础上添加了对时间信息的处理模块. 在未来, 随着新的静态图谱表示模型的出现, 基于新出现模型适应性设计的时间处理模块将会有更多时序模型诞生.
(2)隐式建模(历史信息抽取)方法
时序知识图谱中的时间信息直接建模并容易, 上述显式建模中更多的是通过建模时间造成的影响来间接建模时间信息. 而实体、关系的历史信息亦是时间信息的另一种展现, 其间接展现了时间的变换和影响. 历史信息往往通过3种形式进行体现, 第1种为实体历史信息, 即同一实体在不同时间戳上的图谱中是否存在; 第2种为实体-关系历史信息, 即同一实体-关系对在不同时间戳上的图谱中是否存在且包含的所有关联实体; 第3种为知识(事件)历史信息, 即同一三元组在不同时间戳上的图谱上是否存在. 模型往往针对上述3种历史信息中的某种或多种进行提取, 并设计不同的模块对提取的历史信息进行处理. 由表1可以轻松发现, 历史信息抽取方法远多于时间显式建模方法, 且选择基于结构相关性构建底层嵌入的模型均对历史信息进行抽取并进一步处理.
最早对历史信息抽取的模型为, 2017年Trivedi等人提出的Know-Evolve[38], 他们将时序知识图谱按照时间顺序转换为一个由各时间点静态图谱构建的图谱序列. 并针对这个序列进行编码, 其定义了两个自定义的RNNs, 可以在新的时间下添加新三元组
| $ \left\{\begin{gathered} {\mathbf{s}} = {\tanh}({{\mathbf{W}}_m}\Delta {\tau _s} + {{\mathbf{W}}_{ll}}{\tanh}({{\mathbf{W}}_l}[{\mathbf{s}};{\mathbf{o}};{{\mathbf{r}}_{{p_s}}}])) \\ {\mathbf{o}} = {\tanh}({{\mathbf{W}}_\tau }\Delta {\tau _o} + {{\mathbf{W}}_{ll}}{\tanh}({{\mathbf{W}}_l}[{\mathbf{o}};{\mathbf{s}};{{\mathbf{r}}_{{p_o}}}])) \\ \end{gathered}\right. .$ |
其通过RNN更新实体表示, 并对实体历史信息进行利用. 即实体在
| $ {v^s}(\tau ) = \sigma ({\mathbf{W}}_t^s(\tau - {\tau {'}}) + {{\mathbf{W}}^{hh}}(\sigma ({{\mathbf{W}}^h}({v^s}({\tau {'}}) \oplus {v^s}({\tau {''}}) \oplus {\mathbf{r}})))). $ |
因为Know-Evolve将每个
2018年García-Durán等人提出的TA-TransE/TA-DistMult[40]将谓词标记序列和时间标记序列串联起来, 其是对知识(事件)历史信息进行提取并应用的, 将同一三元组按照所出现的时间顺序构建为一个时间感知谓词序列并使用LSTM对串联的序列进行编码. 将LSTM的最后一个隐藏状态作为时态感知的关系嵌入
自2020年开始, 对于历史信息的抽取方法就开始大量涌现, 仅在2020年就有3个模型RE-Net、TeMP和GHNN.
RE-Net[46]使用RNN对实体历史信息和实体-关系历史信息进行提取和利用. 每个时刻的表示受前一个时刻影响, 即:
| $\left\{ \begin{gathered} {{\mathbf{H}}_\tau } = {\text{RNN}^1}(g({G_\tau }), {{\mathbf{H}}_{\tau - 1}}) \\ {{\mathbf{h}}_\tau }(s, r) = {\text{RNN}^2}(g({N}_\tau ^{(s)}), {{\mathbf{H}}_\tau }, {{\mathbf{h}}_{\tau - 1}}(s, r)) \\ {{\mathbf{h}}_\tau }(s) = {\text{RNN}^3}(g({N}_\tau ^{(s)}), {{\mathbf{H}}_\tau }, {{\mathbf{h}}_{\tau - 1}}(s)) \\ \end{gathered} \right. ,$ |
其中,
TeMP则是选择使用门控循环单元(GRU)来对实体-关系历史信息进行提取和利用, 即:
| $ {{\textit{z}}_{i, \tau }} = {\text{GRU}}({x_{i, \tau }}, \gamma _{i, {\tau ^ - }}^{\textit{z}}{{\textit{z}}_{i, {\tau ^ - }}}), $ |
其中,
| $ {\hat x_{i, \tau }} = \gamma _{i, {\tau ^ - }}^x{x_{i, {\tau ^ - }}} + (1 - \gamma _{i, {\tau ^ - }}^x){x_{i, \tau }}. $ |
GHNN[50]是首个选择基于霍克斯过程对实体进行表示的模型, 霍克斯过程是一种描述实体影响随着时间延续而衰减现象的方法, 其课以捕获时序知识图谱中历史事件对当前或未来事件产生的影响, 并以此来实现时序图谱上的预测. Han等人[50]基于传统霍克斯过程提出了图霍克斯过程, 使用了一个递归神经网络来估计强度函数. 对于一个预测四元组
| $ \lambda (o\mid {s_i}, {r_i}, {\tau _i}, e_i^{h, sr}) = f({{\mathbf{W}}_\lambda }({s_i} \oplus {\mathbf h}(o, {s_i}, {r_i}, {\tau _i}, e_i^{h, sr}) \oplus {{\mathbf{r}}_i}) \cdot {\mathbf{o}}), $ |
其中,
| $ f(x) = \vartheta \log (1 + \exp (x{\text{/}}\vartheta )), $ |
其中,
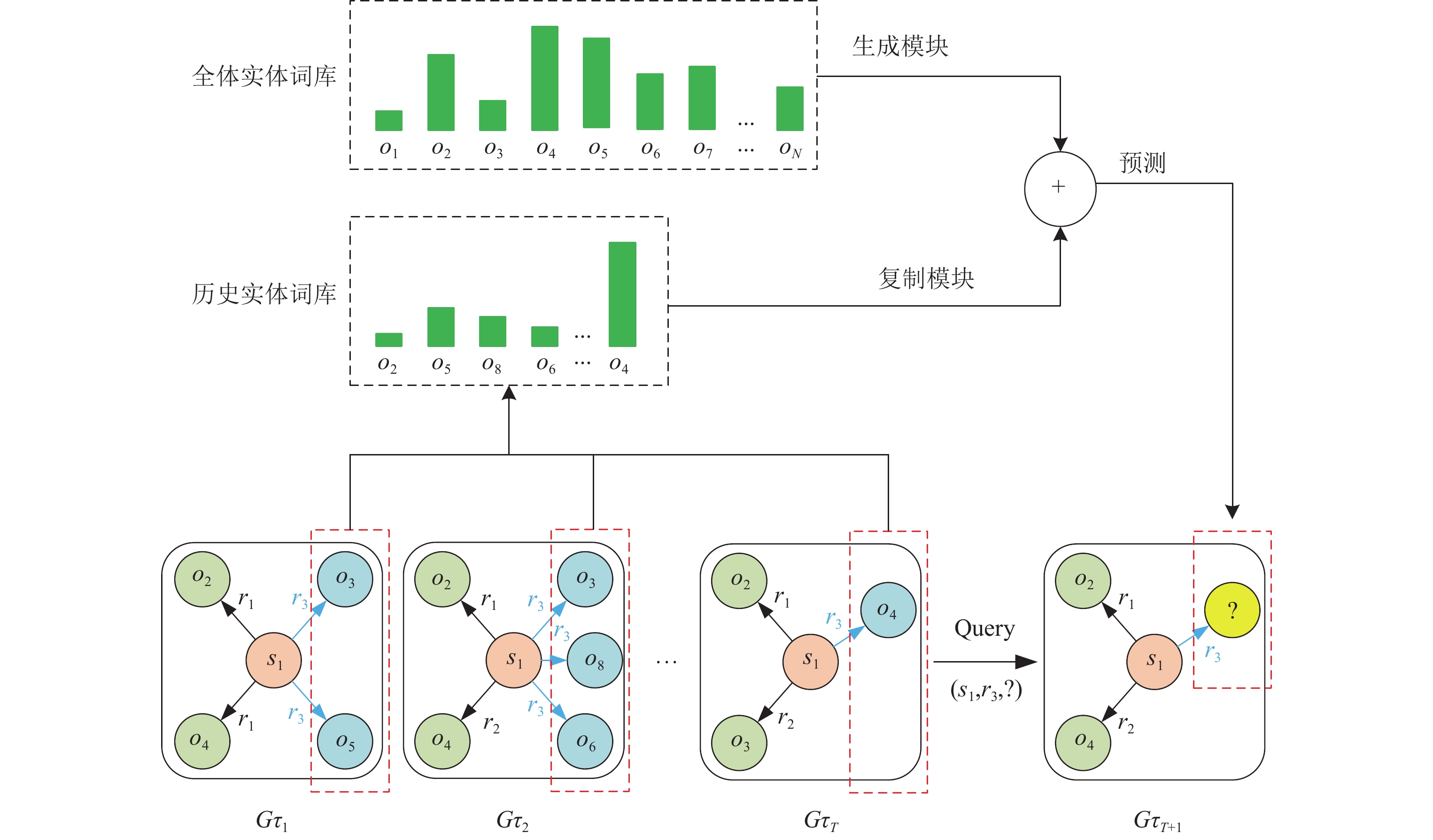
2021年的工作相比于2020年要更多, 有Zhu等人提出的CyGNet[52], 其提出了一个新颖的time-aware副本生成机制, 它不仅可以根据全部的实体词库预测事件, 还能够识别重复的事实并且相应地预测与过去已知事件相关的未来事实. 该模型是一种基于聚合时间观测方法的一种改进, 对过去发生的历史信息即时间观测的聚合, 从而对未来发生的事实进行预测, 模型结构如图8所示. 模型处理训练集来获得训练快照每个
|
图 8 CyGNet的模型结构图 |
| $ {\mathbf H}_{{\tau _k}}^{(s, r)} = {\mathbf{h}}_{\tau {}_1}^{(s, r)} + {\mathbf{h}}_{{\tau _2}}^{(s, r)} + \ldots + {\mathbf{h}}_{{\tau _{k - 1}}}^{(s, r)}. $ |
然后推理模式由复制模式和生成模式两个模块构成. 当预测一个四元组
随后, Li等人提出的RE-GCN[54]设计了进化单元对历史信息进行建模, 进化单元中采用门循环组件和GRU组件对实体和关系的演化进行表示.
| $ {{\mathbf{H}}_\tau } = {{\mathbf{U}}_\tau } \otimes {\mathbf{H}}_\tau ^\omega + (1 - {{\mathbf{U}}_\tau }) \otimes {{\mathbf{H}}_{\tau - 1}} ,$ |
其中,
关系的表示由其所有关联实体的表示聚合而成:
| $ \left\{\begin{gathered} {{\mathbf{R}}_\tau } = {\rm{GRU}}({{\mathbf{R}}_{\tau - 1}}, {\mathbf{R}}'_\tau) \\ {{\vec {\bf{r}}}}\;'_\tau = [pooling({{\mathbf{H}}_{\tau - 1, {\mathcal{V}_{r, \tau }}}}) \oplus {{\vec {\bf{r}}}}] \\ \end{gathered} \right. ,$ |
其中,
同年, Li等人提出的另一个模型CluSTeR[56]中同样采用GRU对历史信息进行编码.
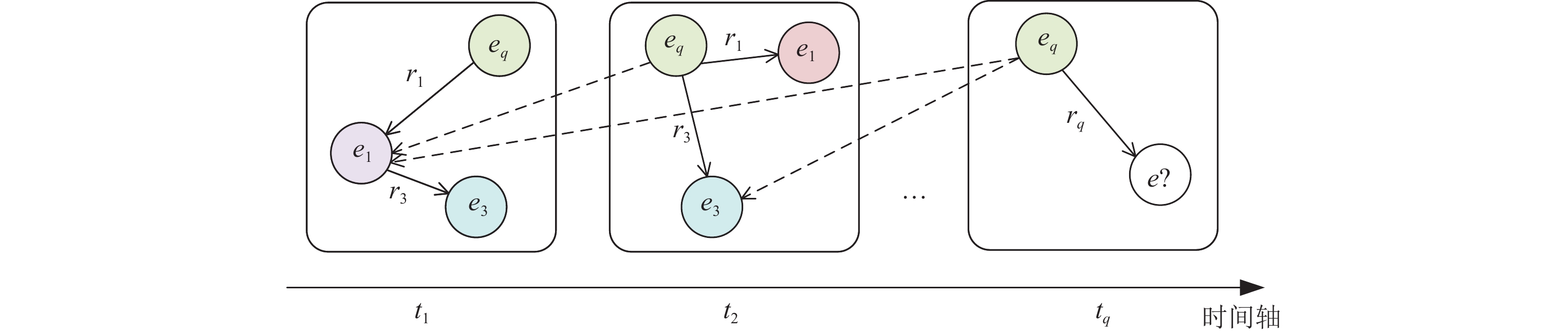
Sun等人提出的TITer[57], 采用的是图谱快照序列的形式, 将时序知识图谱按照时间顺序排列各个时间戳上的静态知识图谱形成一条时序图谱链. 为了从历史时间戳上的图谱中捕获相关历史信息, TITer将不同时间戳上的图谱实体如图9所示按照关系进行跨时间连接. 以此拓展路径搜索时的搜索空间且可以实现跨时间搜索, 将历史信息直接体现在跨时间连接上.
|
图 9 TITer的实体跨时间连接 |
2022年是历史信息抽取模型最多的一年, 从趋势上可以发现, 研究者通过对历史信息的抽取和应用方法改进来不断提升时序知识图谱表示和推理的效果. 且在当前几年, 历史信息的抽取和应用方法改进是较有效的提升模型效果的手段.
Zhang等人提出的EvoExplore[61], 是首个针对时序知识图谱的局部结构和全局结构同时建模的模型, 利用两种结构对历史信息进行特征提取, 极大程度的挖掘了历史的信息. 同时, Zhang等人采用霍克斯过程来作为模型基础, 用以描述时间信息.
| $ \tilde \lambda _{s, o}^r(\tau ) = \mu _{s, o}^r(\tau ) + \theta \mathop \sum \nolimits_{{\tau _i} < \tau } g_{s, o}^r({\tau _i})k(\tau - {\tau _i}).$ |
局部结构建模过程中, 模型对实体的3种时间演变方式(周期性、无周期性和静态)分别进行建模. 针对实体时间演变的表示如下:
| $ {\mathbf{u}}_e^\tau = \sin ({\theta _e} \cdot \tau ) + \tanh ({\omega _e} \cdot \tau ) + {{\mathbf{\nu }}_e}. $ |
同时又采用了两种注意力机制[69]: 关系级注意力和实体级注意力, 来增强实体和关系的表示.
全局结构建模中, Zhang等人参考社交网络中的社区概念, 通过挖掘时序图谱中的社区结构来获得图谱的全局历史信息特征.
Park等人提出的EvoKG[58], 将时序知识图谱表示与推理转换为两个核心子问题事件时间条件密度估计与事件三元组条件密度估计. EvoKG针对事件时间条件密度估计估计采用对数-正态混合, 用以捕获历史对当前的影响; 针对事件三元组条件密度估计采用R-GCN对图结构进行建模, 并用RNN对时间序列进行建模.
Li等人提出的模型CEN[60]在其2021年的工作RE-GCN上进行更一步的探索, 考虑到多跳推理过程中涉及不同时间戳上的信息, 将针对不同推理步长涉及的图谱链进行编码, 直接捕获历史信息在推理过程中的影响.
Liu等人[63]根据真实世界中影响事件发生的各种因素, 提炼出了两种对未来事件发生影响最大的两类因素, 一是历史经验, 这类因素包含了历史中相关事件发生过以及历史中影响此类事件发生的外在因素, 这些历史经验会成为判断未来事件是否发生的重要依据; 二是当前环境状态的影响, 这类因素包含了当前的突发事件或发生改变的外在因素, 这些“新”的影响同样是判断未来事件能否发生的重要依据. 针对上述两类因素, Liu等人设计了一种分布式注意力神经网络DA-Net[63], 用以分别模拟两类因素对事件发生的影响, 也称其为挖掘了时序图谱的历史信息和全局信息. 模型中蕴含了两个注意力层, 第1层用以提取历史重复事件发生的注意力, 保留了历史信息特征; 第2层提取当前突发事件或新环境因素对事件的影响.
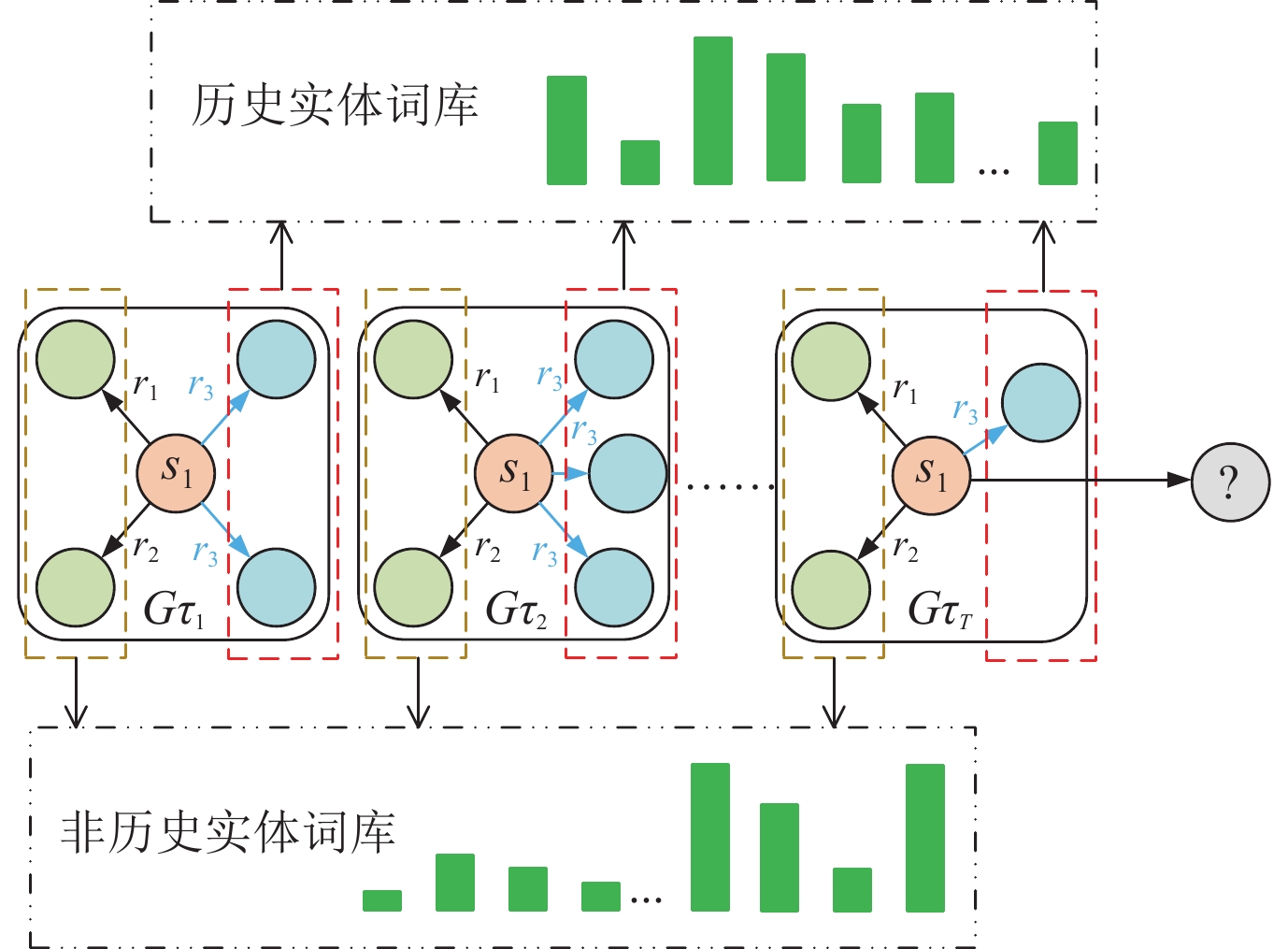
在2023年上半年同样有使用历史信息显示应用的模型CENET[65]被AAAI关注到, 其将对比学习引入到时序图谱推理中, 首先针对缺失的实体是否为历史实体进行预测判断; 然后, 通过判断结果着重在此类中(历史/非历史实体)中进行最终的预测, 模型参考图10. 同时, Xu等人[65]在表示过程中同时考虑历史和非历史信息对实体关系进行建模, 并对历史和非历史信息两种情况分别设计了评价函数:
|
图 10 CENET的时间信息应用 |
| $ {\mathbf{H}}_{his}^{s, r} = \tanh({{\mathbf{W}}_{his}}({\mathbf{s}} \oplus {\mathbf{r}}) + {{\mathbf{b}}_{his}}){{\mathbf{E}}^{\rm{T}}} + {\mathbf{Z}}_\tau ^{s, r}, $ |
| $ {\mathbf{H}}_{nhis}^{s, r} = \tanh({{\mathbf{W}}_{nhis}}({\mathbf{s}} \oplus {\mathbf{r}}) + {{\mathbf{b}}_{nhis}}){{\mathbf{E}}^{\rm{T}}} - {\mathbf{Z}}_\tau ^{s, r}, $ |
其中,
| $ {\mathbf{Z}}_\tau ^{s, r}(o) = \lambda \cdot ({{{\Phi }}_{{\mathbf{F}}_\tau ^{s, r}(o) > 0}} - {{{\Phi }}_{{\mathbf{F}}_\tau ^{s, r}(o) = 0}}), $ |
其中,
| $ {\mathbf{F}}_\tau ^{s, r}(o) = \mathop \sum \limits_{k < \tau } | \{ o\mid (s, r, o, k) \in {\mathcal{G}_k}\} |.$ |
上述对采用历史信息抽取方法的模型进行介绍, 可以发现研究者们对历史信息抽取和应用的手段层出不穷, 创意十足, 从不同方面来挖掘利用时序图谱中的历史信息. 在未来研究中, 对历史信息挖掘方法的开发将不会停止, 会有更多的手段和创意性方法被提出, 会通过历史信息的处理更一步提高时序图谱表示和推理的效果.
(3)对比分析
对比两种信息处理方式参考表3可以明显发现, 时间信息显式建模方法与底层嵌入表示的方法紧密相关, 由于其更多的是针对时间对实体、关系的影响进行建模, 所以对实体、关系的底层表示有极大的依赖性, 同时受到表示框架的影响. 同时此类方法往往有较强的适应性, 即其设计的显式信息建模方法可以适应不同的底层嵌入. 因而, 可以通过数据集和使用场景选择更为适合的底层嵌入, 来获得对时序图谱更好的表示效果.
| 表 3 时间信息利用方法对比分析表 |
而时间信息隐式建模则恰恰相反, 其针对实体提取了历史信息, 并根据历史信息挖掘实体在不同时间戳下的特征. 此类方法, 往往是将时序知识图谱按照时间顺序建模为静态知识图谱序列, 因此研究者们采用适用于时间序列的神经网络来挖掘图谱的时序信息和历史特征. 这类方法不完全依赖底层表示, 重点在于历史信息的挖掘能力. 因此, 在近几年表示框架没有新突破的情况下, 时序表示推理效果依靠历史信息挖掘的能力的不断提升而不断提高. 通过表1, 也恰恰验证了此点.
3.3 推理模块推理模块构建是整个框架的第3个部分, 是能直接体现模型表示效果的模块, 而且推理模块构建方法的选择往往也与底层嵌入的选择和时间信息处理方式息息相关. 时序知识图谱由于其特殊性, 同时具备实体关系的语义信息、图的结构信息等. 因此, 推理可以根据实体关系的语义信息进行构建评价函数, 亦可根据图谱的图结构信息构建评价函数, 还可根据条件概率进行推理. 由表1可以发现, 基于语义推理的模型占了绝大多数, 是当前比较常用的方法. 基于结构推理的方法, 是最近3年出现的推理模块构建方法, 路径推理、强化学习均在推理上有着良好表现.
(1)基于语义推理
基于语义推理的方法是当前主流的选择方案, 因为在传统静态图谱表示推理中, 语义推理也是主流的方法, 至今仍在被研究者们广泛使用.
语义推理主要是依靠实体、关系的语义信息对知识(三元组、四元组、事件)进行真假判定. 最常用且普遍的评价函数为:
| $ f(s, r, o) = ||{\mathbf{s}} + {\mathbf{r}} - {\mathbf{o}}|{|_2} ,$ |
其中, 主语实体、关系和宾语实体
亦或是通过双线性的方式构建评价函数为:
| $ f(s, r, o) = ({\mathbf{s}} \circ {\mathbf{o}}){{\mathbf{r}}^{\rm{T}}}, $ |
其中,
t-TransE、TransE-TAE、Know-Evolve等均是采用上述两的推理过程, 针对上述两种评价函数进行细微调整.
ATiSE[43]同样采用基于语义的推理, 只是其推理评价函数较上述两种有所差异, 其采用的是KL散度来评估实体关系间的相似度.
其实, 可以发现基于语义推理的评价函数的本质就是计算知识中关键元素的语义相似度, 不论是双线性或KL散度[70]均是如此.
(2)基于结构推理
知识图谱的图结构亦是其重要特征, 因此基于图结构进行推理是近几年出现的较为有效的方法之一. 基于结构的推理更多的是借鉴了图表示及推理的方法, 在传统图中, 路径结构特征是其推理的重要参考, 因此在时序知识图谱的推理过程中, 借助图谱中的实体、关系“路径”进行推理成为一个有效的解决方案.
首篇采用路径推理的模型为2021年Han等人提出的xERTE[53]. 其通过对时序知识图谱中的目标实体的邻居节点进行迭代并结合Han等人创新提出的反向表示更细机制来生成子图. 通过生成的子图实现对缺失实体的推理. 由于子图中包含了明确的推理路径, 使得xERTE具备极高的可解释性.
随后, Li等人参考人类推理的双过程理论[71–74]提出的模型CluSTeR[56]将推理分为线索(历史信息捕获)和时间推理两个阶段. 在第1阶段, CluSTeR采用强化学习来从历史信息中搜索预测相关实体的线索. Li等人设计了一个语义策略网络, 根据当前状态和搜索历史, 在忽略时间戳的基础上来计算强化学习中所有动作的概率. 然后, 使用LSTM来对候选线索路径进行嵌入式编码.
第2阶段, Li等人将所有线索按照时间顺序重新构建为图谱序列
CluSTeR因为其独特的机制, 在时序知识图谱推理中具有显著优势, 并在ICEWS和GDELT数据集上进行了实体预测的实验验证.
同年, Sun等人[57]提出的模型TITer同样采用强化学习来进行推理, 且在通用数据集上取得了更为优异的结果.
2022年, Li等人[60]提出的CEN是在推理过程中着重考虑了不同的推理步长对推理造成的影响, 为此设计了长度感知的CNN模块来捕获不同推理步长的独立特征.
上述方法, 仅是现阶段较为具有代表性的基于结构的推理方法, 这类方法着重关注图谱的结构信息, 在推理的过程中同时注重提取推理路径, 因此此类推理方法具有极佳的可解释性. 在当前机器学习模型对于可解释性愈发重视的大环境下, 时序图谱中基于推理的方法在未来几年大有可为.
(3)基于概率推理
这类方法的核心就是将推理过程转换为概率计算的问题.
首个基于概率推理的模型为2020年Jin等人提出的RE-Net[46]. 其将时序知识图谱推理建模为条件概率
2021年Zhu等人提出的CyGNet[52]和Li等人提出的RE-GCN[54]是参考RE-Net进行改进的, 着重在原有的基础上增加了对历史信息的利用, 因此推理过程继续沿用了基于概率计算的方法.
2022年Park等人提出的EvoKG[58], 将整个时序图谱
| $ p(G) = \prod\limits_\tau {p({G_\tau }\mid{G_{ < \tau }})} = \prod\limits_\tau {\prod\limits_{(s, r, o, \tau ) \in {G_\tau }} {p(s, r, o, \tau \mid {G_{ < \tau }})} } . $ |
进一步的, Park等人将
| $ p(s, r, o, \tau \mid{G_{ < \tau }}) = p(\tau \mid s, r, o, {G_{ < \tau }}) \cdot p(s, r, o\mid {G_{ < \tau }}). $ |
至此, 将对概率分布
而同年Liu等人提出的DA-Net[63], 将实体预测
(4)混合推理
混合推理是最近3年的模型中出现的复杂推理过程, 此类模型在推理过程中同时考虑语义、结构两种特征.
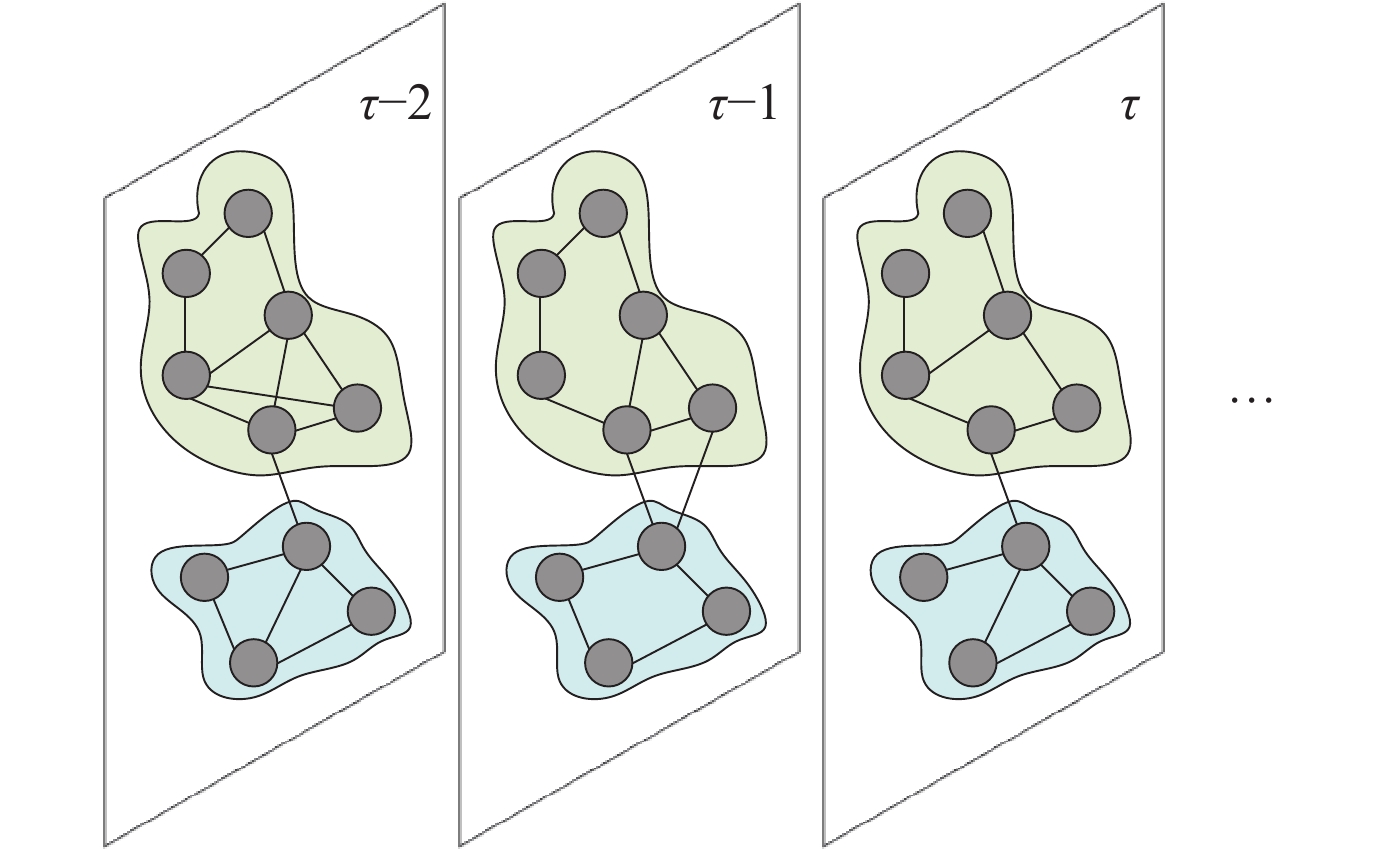
2021年, Zhang等人提出的EvoExplore[61], 同时对时序知识图谱的局部结构和全局结构进行建模. 局部建模, 模型采用基于语义的方法对实体进行推理; 全局建模中, Zhang等人参考社交网络中的社区概念[76,77], 如图11中所示通过挖掘时序图谱中的社区结构来获得图谱的全局特征. 由于同时考虑语义和结构, 使得EvoExplore相比于HyTE和TeMP对时间敏感实体与时间不敏感实体有更好的区分.
|
图 11 EvoExplore的全局结构建模 |
2023年最新的模型CENET[65], 先后利用结构信息针对缺失实体是否为历史实体和利用语义信息对最终实体进行预测.
(5)对比分析
通过上述几种使用不同推理方法模型的介绍, 通过表4可以发现推理模块的评价函数发挥作用都是与时序知识图谱的特性紧密相关的, 无论是实体间的语义相关性还是图谱中的结构特性. 同时, 推理模块的设计与底层表示的选择亦有关联, 尤其是基于语义推理的模块设计, 因其本身依赖实体的语义相似度, 所以其与实体的底层表示选择最为依赖. 因此这类方法, 推理效果更多地依赖于底层表示框架的选择. 优点是构建简洁, 不需要复杂的模块构建; 但是不可避免的缺点就是, 推理模块本身不能为模型带来更好的增益效果, 成为底层表示框架的附属结构.
| 表 4 推理方法对比分析表 |
基于结构的推理模块与语义的恰恰相反, 其由于更多的关注图谱的结构特性, 因此在某种程度上, 是对实体表示中语义信息的一种补充. 因此, 在推理性能上, 会有较好的表现. 而且模型可以针对推理模块进行进一步设计, 不在受限于底层嵌入设计. 且由于这类模型基于路径结构信息进行推理, 预测推理更具有可解释性.
基于概率推理的模型, 往往与图卷积的底层嵌入相关联, 且在后续针对概率进行初步处理时会对其进行拆分分别计算.
随着表示推理模型性能的不断提升, 单一模式的推理模块很难在性能上做出明显突破, 为此, 近年研究者们结合语义和结构两种时序知识图谱特征提出混合推理模型, 其由于包含多种特征, 往往具有较好的推理效果.
3.4 特殊场景定制设计特殊场景定制设计是研究者在模型设计之初最先考虑的, 根据模型使用场景, 针对性地对模型进行设计. 时序知识图谱表示和推理在实际应用中有许多特殊场景, 本文将现有针对特殊场景设计的模型按照场景归纳为增量/在线场景、小/零样本场景和开放世界场景. 由表1可以发现, 针对特殊场景的模型研究是在2021年之后才逐步开始的, 这是由于时序图谱的表示推理效果随着多年研究愈来愈显著, 精度逐步满足了现实应用的需求, 随着时序知识图谱的应用越来越广泛, 人们对于特定场景下的时序知识图谱的需求也越来越迫切. 例如, 在金融领域, 时序知识图谱可以用于预测股票价格、分析市场趋势等; 在医疗领域, 时序知识图谱可以用于疾病预测、药物研发等. 因此, 为不同领域的特殊场景构建定制化的时序知识图谱, 能够更好地满足用户的需求, 提高应用效果. 下面分别对适用于几种特殊场景的模型进行介绍.
(1)增量/在线场景
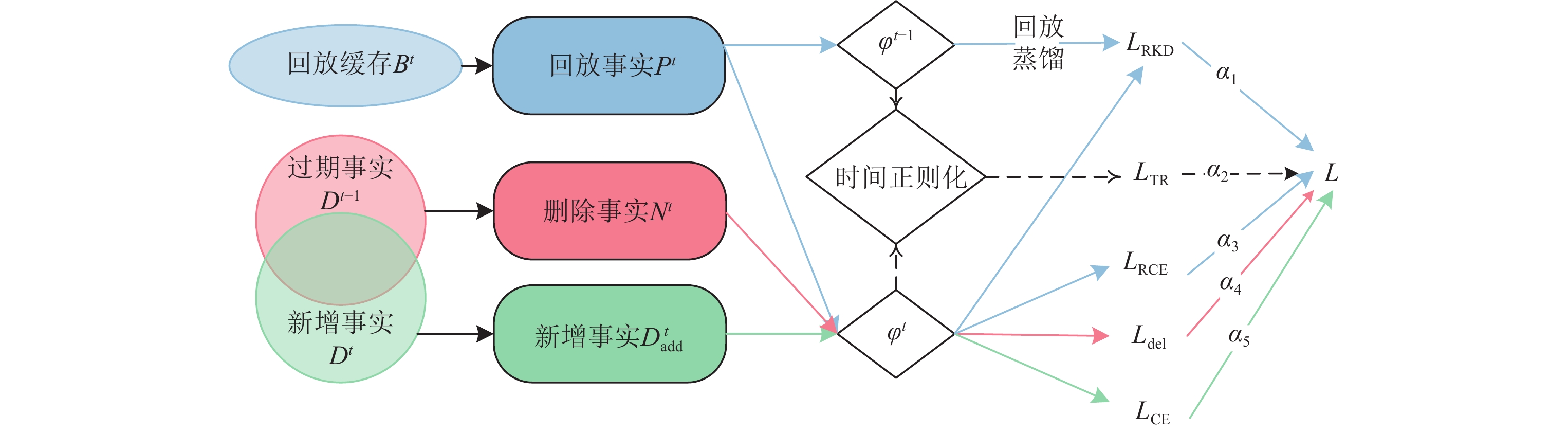
TIE[55]是一种适用于特殊场景的增量式表示模型. Wu等人[55]针对原有增量式表示方法中的灾难性遗忘[78]、事实变化无法识别与训练效率低等问题, 提出了一种增量式的时序知识图谱表示框架时间感知增量嵌入(TIE), 可以针对随时增加和更新的任意时间节点的事实进行增量式训练, 主要采用了经验回放和时间正则化技术来解决表示模型在微调时所遇到的灾难性遗忘问题, 模型结构如图12所示.
|
图 12 TIE的模型结构 |
与此同时, TIE使用从最近时间间隔中删除的事实作为负例训练子集, 以解决其他时序知识表示模型所遇到的不妥协问题. 通过研究发现, 时序知识图谱主要由持久的事实组成, 即事实通常持续时间较长, 相邻时间间隔之间不会发生剧烈变化. 因此, 所提出的框架只在每个时间间隔中使用新添加的事实来对模型进行微调.
模型CEN[60]同样通过在线学习, 实现了实时的对知识图谱推理过程的提取.
(2)小/零样本场景
Xia等人[64]通过分析发现现有大部分模型在预测时主要依赖历史信息, 近几年模型均在针对历史信息的挖掘上取得了突破, 从而提高了推理精度. 但是, 这背后针对具有少量历史信息实体的预测精度并未有显著提升, 甚至缺少了对新实体事实预测的能力. 为此, Xia等人提出了一种针对时序知识图谱的元学习框架MetaTKG[64], 将时序预测转换为时序元任务, 旨在提高原模型对新数据的适应能力, 提高原模型针对新实体的训练精度.
(3)开放世界场景
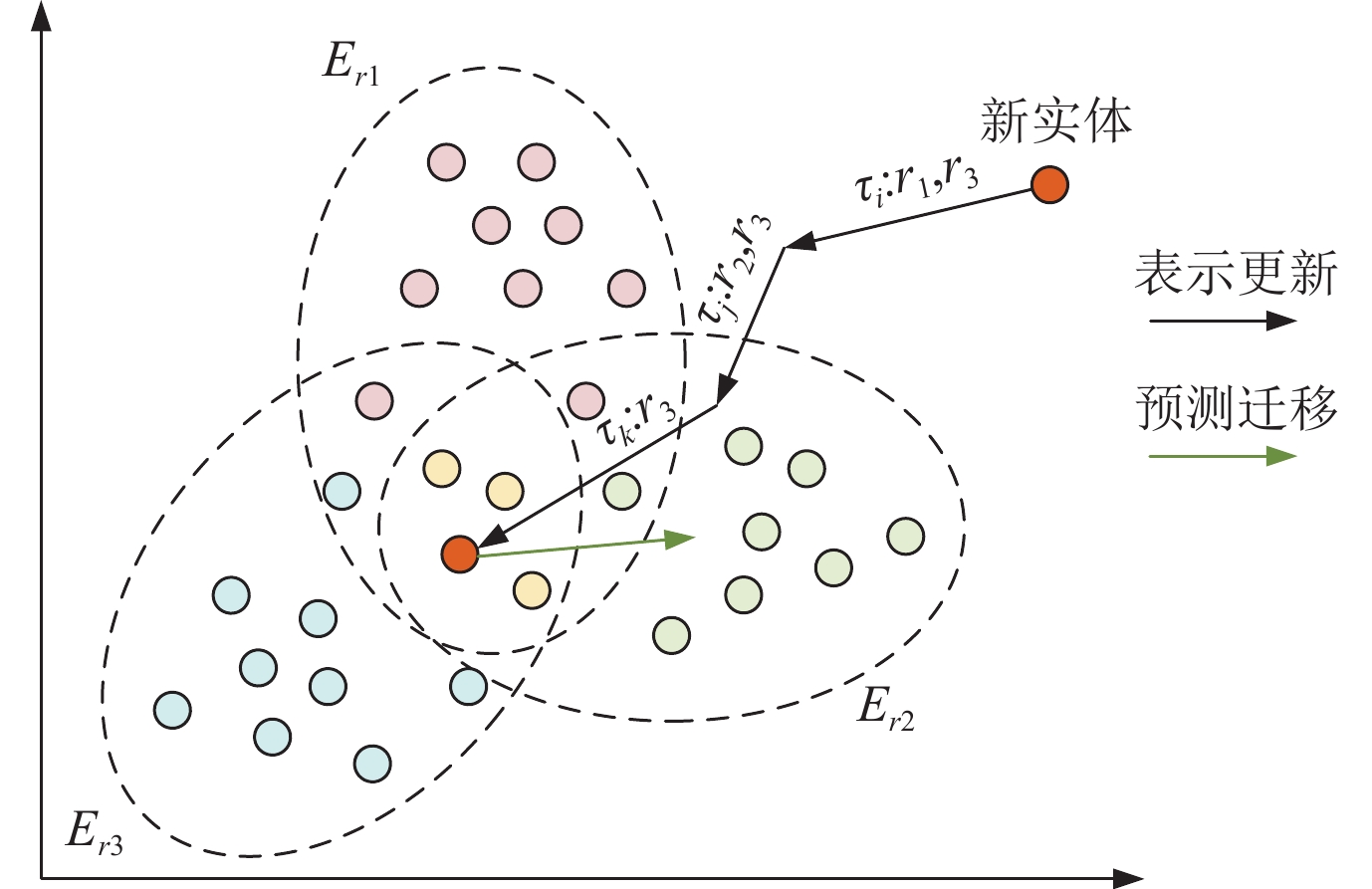
时序知识图谱随着时间的推移, 在应用中会不断有新的实体出现, 新实体未曾在原有图谱中出现, 因此无法对其进行有效且准确的建模, 因此会影响模型的推理效果. 而TITer[57]相比于其他推理模型, 更具有特色的优势是可以针对新实体进行推理预测. 新实体与原有图谱缺少直接联系, 因此很难对其进行精准表示, 难以依托图谱信息对其进行推理和预测. TITer通过待预测三元组中的关系来对新实体的类型进行初步判断, 并设计了一种感应均值(IM)算法, 利用已训练的同类型实体表示来设置新实体的初始值, 新实体预测如图13所示, 通过新实体不同时刻与关系类之间的共现关系来逐步更新新实体的表示, 最后通过所属类进一步生成新实体的表示. 以此, 极大增加了新实体与时序图谱之间的关联, 进而通过模型对其进行推理和预测, 极大提高了针对新实体的预测精度.
|
图 13 TITer的新实体预测 |
时序图谱在预测推理过程中, 存在许多新的事件, 即没有历史信息可以依赖的事件(事件未在历史中出现过). 针对这类事件的预测, 模型的准确性往往都差强人意.
CENET[65]则通过对比学习方法首先对缺失的实体是否为历史实体进行预测判断, 进而提升新事件的预测概率.
(4)对比分析
上述3种特殊场景并不能涵盖所有的时序知识图谱特殊应用场景, 其仅是现阶段具有针对性设计模型的3种, 随着时序图谱的继续发展和研究, 适用于其他特殊场景的时序知识图谱也将逐渐被研究者关注. 就现阶段而言, 研究针对开放世界场景的时序图谱是一个较为热门的研究方向.
3.5 小 结在预测任务中, 历史信息往往是预测推理的重要依据, 对历史信息的运用与特征挖掘往往决定了模型的预测精度. 通过上述对各个模型的介绍, 可以发现, 自2016年时序知识表示相关的任务提出以来, 2020年开始进入研究高峰期, 大量的模型被提出, 但是这个阶段的模型往往在原有静态图谱表示的基础上进行相关的拓展与演化. 而进入2021年, 研究者们开始着重关注于对于历史信息的应用, 此时模型对于时序图谱的表示能力得到了加强, 预测精度开始有了一个小跃升. 2022年, 研究者除了在针对历史信息进行进一步挖掘和高效利用的同时, 开始了针对数据集中数据分布的特性进行分析, 针对其中新实体、新事件进行针对性的特殊处理, 使得预测推理上有一次有了显著的提升. 与此同时, 近几年较为风靡的算法框架, 诸如, 强化学习、对比学习等均被研究者引入到时序表示的模型中. 并且, 特殊场景下, 也有研究者进行研究并取得了一定成果.
4 时序知识图谱通用数据集时序知识图谱表示学习研究工作使用的数据集通常为如下4类, 包括GDELT (global database of events, language, and tone), ICEWS (integrated crisis early warning system), YAGO和Wikidata. 根据不用的任务, 又可详细分为如表5中所统计的7个不同数据集.
| 表 5 通用数据集基本统计表 |
● GDELT. GDELT是一个全球事件、语言、语气数据库, 它包含两个主要的数据集: 事件数据库和全球知识图谱(GKG). GDELT记录了自1969年以来的新闻报道, 每15 min更新1次, 用于跟踪世界各地的事件和趋势. 是一个由事件、主题和实体组成的知识图谱, 它从事件数据库中提取信息, 并根据实体之间的关系构建一个动态的知识图谱.
在2017年, Trivedi使用GDELT中的数据, 构建了一个包含
2020年, Goel等人[42]根据此时序图数据改造出训练、验证和测试集用以时序知识图谱补全任务.
● ICEWS. ICEWS (integrated crisis early warning system)是一个综合危机早期预警系统, 用于存储具有时间戳的政治事件. 该系统使用逻辑谓词(如“访问”“谈判”等)将实体(如“国家”“总统”等)与许多其他实体联系起来, 以创建一个事件网络. 这个存储库以转储形式组织, 其中包含1995–2015年发生的事件.
由于ICEWS系统可以帮助了解国际关系和政治事件之间的联系, 因此该系统可以被用于研究国际关系、政治学和社会科学等领域. García-Durán等人根据ICEWS创建了两个时序知识图谱数据集, 为ICEWS2014和ICEWS2005-15[40]. 其中, 前者覆盖时间范围较短, 只包含2014年发生的所有事件, 其时间粒度为24 h, 包含
● YAGO. YAGO是一个源自维基百科、WordNet和其他数据源的大型知识数据库[79, 80]. 节点包含人、组织和事件等实体类型; 关系包括诸如“wasBornIn”“isLocatedIn”等; 时间信息格式为“occursSince”和“occursUntil”. 2016年Jiang等人[37]根据此构建了一个包含
● Wikidata. 2018年Leblay等人利用维基数据构建了一个时序知识库[81]. 同年, García-Durán等人从中筛选出常用的实体和关系, 用以时序知识图像相关的实验研究. 其中包含
时序知识图谱表示推理通常在上节介绍的通用数据集上进行实验验证, 不同的模型方法在提出时具有优异表现, 但是不同模型因为结构差异性和研究侧重点不同, 在不同数据集上会有差异性的特殊表现. 下面, 本文结合各个作者论文中的实验结果, 对其中的一些特殊现象进行分析, 从而发现各个模型的优势点, 为后续研究者们提供参考和启发. 同时本文还对通用的5个数据集进行了更为详细的数据分析.
本文针对数据集在表6分别统计了训练集时间数量、测试集新时间数量、稀疏度、测试集新实体比例、新事件比例等信息. 通过这些信息, 不难发现, 测试集中有较多的新时间, 因此在预测过程中会有很多属于未来预测. 但是在当前的很多模型中, 未对实体预测和未来预测任务进行区分, 尤其是未对数据集进行特殊过滤处理. 那么最终的实验结果并不能完全展示模型本身的性能, 模型间的对比也会存在不公平的情况.
| 表 6 数据集详细分析 |
同时, 通过表6可以发现, 时序知识图谱在每个时间戳上的静态图谱都是非常稀疏的, 单纯的针对静态图谱进行建模很难获取很好的实体表示, 因此更多的挖掘图谱或实体历史信息可以得到更准确的实体关系表示, 结合表1和表7可以发现, 最近几年采用历史信息抽取的模型(如: CENET、EvoExplore、CyGNet、RE-Net等)逐渐涌现并表现出更好的结果.
| 表 7 典型模型在实体预测任务上的表现一览表 (%) |
通过第4节数据集的介绍, 可以发现ICEWS和GDELT数据集是同一类的, 其中以记录全球发生的实时事件为主, 时间粒度为1天, 大量的活跃实体与新事件. 而Wikidata和YAGO数据集是在知知识库的基础上进行构建, 常识、事实类的知识较多, 且时间粒度为1年, 实体活跃度相比于ICEWS和GDELT要低, 且新事件比例较少. 结合表7与各论文中的实验结果可以发现, 表示模型在Wikidata和YAGO上的表现要远远优于ICEWS和GDELT. 这是由于新事件缺失历史信息作为参考, 预测精度极大受限, 而Wikidata和YAGO中新事件的比例要小于ICEWS和GDELT.
而在针对主语实体和宾语实体预测时, 新事件比例也不完全相近, 以Wikidata数据集为例, 宾语实体相关的新事件占比为37.3%, 主语实体相关的新事件占比高达76.6%. 这种极大差异导致的失衡, 使得一般方法对实体预测的精度受到极大影响. CENET模型依靠着其针对历史与非历史信息分别建模的独特手段, 解决了这种失衡问题, 极大地提升了Wikidata数据集上实体预测的精度. 结合表7中的结果, 其将精度提升了20个百分点[65].
在预测任务中, 新实体、新事件由于其与整体结构关联性较低往往是预测的难点. 一般模型不针对性进行相关处理很难对其有较好的预测精度. 由表6可以发现, 在Wikidata和YAGO的测试集中, 存在远高于其他3个数据集的新实体比例. 因此结合表8中的结果可以发现, 模型TITer通过提出感应均值算法针对性的解决新实体预测问题后, 对整体模型精度带来了极大的提升, 在两个数据集上均带来了超过20个百分点的提高[56].
| 表 8 典型模型在未来事件预测任务上的表现一览表 (%)[56] |
结合上述分析可以发现, 当前的通用数据集数据分布不同, 各自特点也不相同, 随着模型研究的愈发深入, 各种特异性优势被开发, 简单地使用测试数据集不能准确对其评估, 需要研究者根据模型特点, 针对性地对测试集进行划分和处理, 以此提高对模型效果判定的准确性.
6 发展趋势与展望在前文中, 本文对知识表示推理的各个模型进行了介绍, 并且在节末通过时间脉络对知识表示推理近几年的技术路线进行了简单归纳. 从底层嵌入到时间信息处理, 再到新实体、新事件的针对性建模. 模型的表示能力在逐年增加, 预测推理的精度也逐年提升, 甚至在Wikidata和YAGO数据集上有了飞跃进步.
但是通过对上述所有模型的介绍和分析后, 不难发现, 现有的所有模型在底层嵌入层面上依然没有跳出几个常用的框架, 诸如, 基于语义相关性、结构相关性构建的静态知识图谱表示. 并不是说在常用框架下, 模型不能有良好的表现, 但是研究者们已经开始逐步接近这类模型框架表示能力的上限了. 如果近几年, 不能有基础框架的创新, 时序表示模型的发展将迅速陷入瓶颈, 而当前时序表示模型在推理上的精度还远没有达到可以在应用中发挥重要作用的标准, 整体预测效果在实际中仍然存在极大问题.
时序知识图谱对于大数据智能具有重要意义, 在自然语言处理、信息检索、智能推荐和智能问答等领域中都具有至关作用, 但是现有精度却限制了它的发展. 在未来的一段时间, 时序知识图谱表示与推理的研究应该会在如下几个方面进行突破.
(1)底层表示框架的创新
底层嵌入表示框架是整个表示的核心, 现有总结的两个底层表示框架不足以支撑时序知识图谱表示捅破现有困境, 实现表示能力大幅跃升和预测推理精度跃迁式提高. 因此, 在今后的研究中, 基础表示框架的创新仍然是重中之重, 一旦有新框架体系的创新, 将立刻会有大量研究者基于此提出更优秀的时序表示模型, 带动整个时序知识图谱相关研究的发展.
当然, 由于时序知识图谱的基础属性, 其技术与知识图谱研究和图研究有极大的关联性. 因此, 有极大概率, 基础表示框架的创新将会在知识图谱表示或者图表示方向率先做出突破. 后续研究者可以适当地将研究目标转移到知识图谱和图上面, 也同样可以针对时序图谱的特殊属性时间进行技术突破.
(2)时间信息处理的深入探索
现有基础表示框架的潜力还没有完全挖掘, 即基于现有的框架进行研究仍有较大上升空间. 研究者们可以继续针对时序知识的时间信息处理方法进行深入探索, 也可以去深度分析时间信息对当前预测推理的影响因素. 这两个方面的研究依然可以作为当前时序表示的研究重点, 着重进行突破.
(3)新实体、新事件等新特性的针对研究
时序图谱的数据具有很多独有的特性, 且在不同的数据集和应用场景中亦有不同的特性, 诸如新实体、新事件占比高等. 针对这些特性进行针对性研究将在现有框架基础上对模型预测推理精度得到提升. 这个方面的研究类似于知识图谱中的开放世界知识图谱相关的研究, 旨在找到一种合理的方式将新实体或新事件与整个时序知识图谱关联起来, 从而实现语义或者结构上的连通, 保证了新实体表示的准确性. 针对这方面的研究, 研究者们可以从推荐系统冷启动方向研究中找到灵感.
此外当前大部分模型在处理测试集时, 并未对新实体相关的预测进行筛选, 尤其是针对待预测实体为新实体时, 当前模型均不能进行预测. 因此现有实验就不能准确地对模型的表现进行准确展示, 在一定程度上对模型的能力有所低估. 后续可以依据新实体对测试数据集进行更为详细地划分, 以此来提升模型评估的准确性, 亦可验证针对开放世界特殊场景模型的效果. 同时, 研究者可以针对现有模型不能预测待预测实体为新的难题进行相关的研究和突破.
(4)预测推理的可解释性研究
除了对时序知识表示新方法的研究以外, 近几年, 研究者们对各领域的预测推理的可解释性越来越关注, 人们不再单一执着于对精度的提升, 而是对推理的依据越发的关心. 推理的解释性成为各方争相研究的热点. 因此未来时序表示推理的可解释性研究将越发的被重视, 不能简简单单地将时序知识表示为嵌入向量就高枕无忧, 反而需要对表示和推理的可解释性进行相关说明和分析. 未来几年, 研究者可以将时序知识表示推理的可解释性研究作为自己的研究方向.
(5)增量/在线、小样本等特殊场景下的表示研究
随着时序知识图谱的研究愈发深入, 其在现实场景下的应用也将日益增加, 那么各种特殊应用场景亦对表示模型提出更多的要求. 随着时序知识图谱规模的增加, 增量/在线学习场景就必不可或缺, 因此针对此的研究亦是时序图谱表示的下个热点. 与此同时, 时序图谱在特殊领域提供知识支撑时, 可能面临特殊领域特殊实体训练数据稀少等情况, 那么此时少样本情况下的表示和推理研究就至关重要. 因而, 研究者可以从应用场景的角度出发, 着力于对时序知识图谱在特殊应用场景下的定制化研究.
(6)时序知识图谱领域其他关键技术的研究
时序知识图谱发展至今才有近7年, 依然处在发展的初级阶段, 几乎所有时序领域知识图谱还处在构建完善阶段, 远远没有达到投入前沿应用并发挥显著作用的地步. 除了在时序表示方面有大量的研究外, 其他相关的相关技术, 诸如: 时序知识抽取、时序实体对齐、时序图谱融合与时序知识图谱质量评估等均处于亟待开发创新的阶段. 因此, 研究者们可以在现有时序表示的基础上进行其他关键技术的研究. 这将对补全整个时序知识图谱领域研究的拼图起到至关作用, 加速时序知识图谱的应用落地, 从而从实用反馈中获得新的研究方向和思路.
7 总 结本文对时序知识图谱进行了简要介绍, 其中着重针对时序知识表示推理技术进行了梳理, 将时序知识图谱自开创到现在的绝大部分优秀有代表性的模型进行了归纳和简述, 且总结提出了一个时序知识图谱表示与推理模型的理论框架, 并依据此对各个模型进行了对比分析. 同时, 本文梳理出了时序知识表示推理发展的基础脉络, 对该领域当前遇到的问题和未来可能遭遇的瓶颈进行说明. 最后, 本文又对时序知识图谱未来的研究方向进行了划分, 从底层表示框架的创新、时间信息处理的深入探索、新实体等新特性针对研究、预测推理的可解释性研究、增量/在线等特殊场景下的表示研究和时序知识图谱领域其他关键技术研究6个方面指明了时序知识图谱的未来研究方向和趋势, 旨在为后续研究者们提供参考.
| [1] |
Singhal A. Introducing the knowledge graph: Things, not strings. 2012. http://googleblog.blogspot.com/2012/05/introducing-knowledge-graph-things-not.html
|
| [2] |
Wang M, Wang HF, Li BH, Zhao X, Wang X. Survey on key technologies of new generation knowledge graph. Journal of Computer Research and Development, 2022, 59(9): 1947-1965(in Chinese with English abstract).
[doi:10.7544/issn1000-1239.20210829] |
| [3] |
Ni CC, Liu KS, Torzec N. Layered graph embedding for entity recommendation using Wikipedia in the Yahoo! knowledge graph. In: Companion Proc. of the 2020 Web Conf. Taipei: ACM, 2020. 811–818. [doi: 10.1145/3366424.3383570]
|
| [4] |
Chen ZY, Zhao X, Liao JZ, Li XY, Kanoulas E. Temporal knowledge graph question answering via subgraph reasoning. Knowledge-based Systems, 2022, 251: 109134.
[doi:10.1016/j.knosys.2022.109134] |
| [5] |
Ji SX, Pan SR, Cambria E, Marttinen P, Yu PS. A survey on knowledge graphs: Representation, acquisition, and applications. IEEE Trans. on Neural Networks and Learning Systems, 2022, 33(2): 494-514.
[doi:10.1109/TNNLS.2021.3070843] |
| [6] |
Liu Q, Li Y, Duan H, Liu Y, Qin ZG. Knowledge graph construction techniques. Journal of Computer Research and Development, 2016, 53(3): 582-600(in Chinese with English abstract).
[doi:10.7544/issn1000-1239.2016.20148228] |
| [7] |
Kuzey E. Populating knowledge bases with temporal information [Ph.D. Thesis]. Saarbrücken: Saarland University, 2016.
|
| [8] |
Jiang TS, Liu TY, Ge T, Sha L, Li SJ, Chang BB, Sui ZF. Encoding temporal information for time-aware link prediction. In: Proc. of the 2016 Conf. on Empirical Methods in Natural Language Processing. Austin: ACL, 2016. 2350–2354. [doi: 10.18653/v1/D16-1260]
|
| [9] |
Xu YX, Zhao JF, Wang YS, Xie B, Yang K. Temporal knowledge graph representation learning. Computer Science, 2022, 49(9): 162-171(in Chinese with English abstract).
[doi:10.11896/jsjkx.220500204] |
| [10] |
Zhang YJ, Li PF, Zhu QM. Event temporal relation classification method based on self-attention mechanism. Computer Science, 2019, 46(8): 244-248(in Chinese with English abstract).
[doi:10.11896/j.issn.1002-137X.2019.08.040] |
| [11] |
Bordes A, Usunier N, García-Durán A, Weston J, Yakhnenko O. Translating embeddings for modeling multi-relational data. In: Proc. of the 26th Int’l Conf. on Neural Information Processing Systems. Lake Tahoe: Curran Associates Inc., 2013. 2787–2795.
|
| [12] |
Kazemi SM, Poole D. SimplE embedding for link prediction in knowledge graphs. In: Proc. of the 32nd Int’l Conf. on Neural Information Processing Systems. Montréal: Curran Associates Inc., 2018. 4289–4300.
|
| [13] |
Yang BS, Yih WT, He XD, Gao JF, Deng L. Embedding entities and relations for learning and inference in knowledge bases. In: Proc. of the 3rd Int’l Conf. on Learning Representations. San Diego: ICLR, 2015.
|
| [14] |
Sun ZQ, Deng ZH, Nie JY, Tang J. RotatE: Knowledge graph embedding by relational rotation in complex space. In: Proc. of the 7th Int’l Conf. on Learning Representations. New Orleans: ICLR, 2019.
|
| [15] |
Yao L, Mao CS, Luo Y. Graph convolutional networks for text classification. In: Proc. of the 33rd AAAI Conf. on Artificial Intelligence and the 31st Innovative Applications of Artificial Intelligence Conf. and the 9th AAAI Symp. on Educational Advances in Artificial Intelligence. Honolulu: AAAI, 2019. 7370–7377. [doi: 10.1609/aaai.v33i01.33017370]
|
| [16] |
Schlichtkrull M, Kipf TN, Bloem P, van den Berg R, Titov I, Welling M. Modeling relational data with graph convolutional networks. In: Proc. of the 15th Int’l Conf. on the Semantic Web. Heraklion: Springer, 2018. 593–607. [doi: 10.1007/978-3-319-93417-4_38]
|
| [17] |
Hawkes AG. Spectra of some self-exciting and mutually exciting point processes. Biometrika, 1971, 57(1): 83-90.
[doi:10.1093/biomet/58.1.83] |
| [18] |
Mei HY, Eisner JM. The neural Hawkes process: A neurally self-modulating multivariate point process. In: Proc. of the 31st Annual Conf. on Neural Information Processing Systems. Long Beach: NIPS, 2017. 6754–6764.
|
| [19] |
Wang Z, Zhang JW, Feng JL, Chen Z. Knowledge graph embedding by translating on hyperplanes. In: Proc. of the 28th AAAI Conf. on Artificial Intelligence. Québec City: AAAI, 2014. 1112–1119. [doi: 10.1609/aaai.v28i1.8870]
|
| [20] |
Lin YK, Liu ZY, Sun MS, Liu Y, Zhu X. Learning entity and relation embeddings for knowledge graph completion. In: Proc. of the 29th AAAI Conf. on Artificial Intelligence. Austin: AAAI, 2015. 2181–2187. [doi: 10.1609/aaai.v29i1.9491]
|
| [21] |
Ji GL, He SZ, Xu LH, Liu K, Zhao J. Knowledge graph embedding via dynamic mapping matrix. In: Proc. of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th Int’l Joint Conf. on Natural Language Processing. Beijing: ACL, 2015. 687–696. [doi: 10.3115/v1/P15-1067]
|
| [22] |
Sutskever I, Salakhutdinov R, Tenenbaum JB. Modelling relational data using Bayesian clustered tensor factorization. In: Proc. of the 22nd Int’l Conf. on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2009. 1821–1828.
|
| [23] |
Johnson JD, Li JH, Chen ZS. Reinforcement learning: An introduction: R.S. Sutton, A.G. Barto, MIT Press, Cambridge, MA 1998, 322 pp. ISBN 0-262-19398-1.. Neurocomputing, 2000, 35(1–4): 205-206.
[doi:10.1016/S0925-2312(00)00324-6] |
| [24] |
Xiong WH, Hoang T, Wang WY. DeepPath: A reinforcement learning method for knowledge graph reasoning. In: Proc. of the 2017 Conf. on Empirical Methods in Natural Language Processing. Copenhagen: ACL, 2017. 564–573. [doi: 10.18653/v1/D17-1060]
|
| [25] |
Das R, Dhuliawala S, Zaheer M, Vilnis L, Durugkar I, Krishnamurthy A, Smola A, McCallum A. Go for a walk and arrive at the answer: Reasoning over paths in knowledge bases using reinforcement learning. In: Proc. of the 6th Int’l Conf. on Learning Representations. Vancouver: ICLR, 2018.
|
| [26] |
Zhang W, Paudel B, Zhang W, Bernstein A, Chen HJ. Interaction embeddings for prediction and explanation in knowledge graphs. In: Proc. of the 20th ACM Int’l Conf. on Web Search and Data Mining. Melbourne: ACM, 2019. 96–104. [doi: 10.1145/3289600.3291014]
|
| [27] |
Niu GL, Zhang YF, Li B, Cui P, Liu S, Li JY, Zhang XW. Rule-guided compositional representation learning on knowledge graphs. In: Proc. of the 34th AAAI Conf. on Artificial Intelligence. New York: AAAI, 2020. 2950–2958. [doi: 10.1609/aaai.v34i03.5687]
|
| [28] |
Castro FM, Marín-Jiménez MJ, Guil N, Schmid C, Alahari K. End-to-end incremental learning. In: Proc. of the 15th European Conf. on Computer Vision. Munich: Springer, 2018. 241–257. [doi: 10.1007/978-3-030-01258-8_15]
|
| [29] |
Rebuffi SA, Kolesnikov A, Sperl G, Lampert CH. iCaRL: Incremental classifier and representation learning. In: Proc. of the 2017 IEEE Conf. on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017. 5533–5542. [doi: 10.1109/CVPR.2017.587]
|
| [30] |
aBarry M, Bifet A, Chiky R, El Jaouhari S, Montiel J, El Ouafi A, Guerizec E. Stream2Graph: Dynamic knowledge graph for online learning applied in large-scale network. In: Proc. of the 2022 IEEE Int’l Conf. on Big Data. Osaka: IEEE, 2022. 2190–2197. [doi: 10.1109/ BigData55660.2022.10020885]
|
| [31] |
Vilalta R, Drissi Y. A perspective view and survey of meta-learning. Artificial Intelligence Review, 2002, 18(2): 77-95.
[doi:10.1023/A:1019956318069] |
| [32] |
Chen MY, Zhang W, Zhang W, Chen Q, Chen HJ. Meta relational learning for few-shot link prediction in knowledge graphs. In: Proc. of the 2019 Conf. on Empirical Methods in Natural Language Processing and the 9th Int’l Joint Conf. on Natural Language Processing. Hong Kong: ACL, 2019. 4217–4226. [doi: 10.18653/v1/D19-1431]
|
| [33] |
Li XW, Ma JM, Yu J, Xu TY, Zhao MK, Liu HW, Yu M, Yu RG. HAPZSL: A hybrid attention prototype network for knowledge graph zero-shot relational learning. Neurocomputing, 2022, 508: 324-336.
[doi:10.1016/j.neucom.2022.07.038] |
| [34] |
Wang YH, Xiao WD, Tan Z, Zhao X. Caps-OWKG: A capsule network model for open-world knowledge graph. Int’l Journal of Machine Learning and Cybernetics, 2021, 12(6): 1627-1637.
[doi:10.1007/s13042-020-01259-4] |
| [35] |
Shi BX, Weninger T. Open-world knowledge graph completion. In: Proc. of the 32nd AAAI Conf. on Artificial Intelligence. New Orleans: AAAI, 2018. 1957–1964. [doi: 10.1609/aaai.v32i1.11535]
|
| [36] |
Shah H, Villmow J, Ulges A, Schwanecke U, Shafait F. An open-world extension to knowledge graph completion models. In: Proc. of the 33rd AAAI Conf. on Artificial Intelligence. Honolulu: AAAI, 2019. 3044–3051. [doi: 10.1609/aaai.v33i01.33013044]
|
| [37] |
Jiang TS, Liu TY, Ge T, Sha L, Chang BB, Li SJ, Sui ZF. Towards time-aware knowledge graph completion. In: Proc. of the 26th Int’l Conf. on Computational Linguistics. Osaka: ACL, 2016. 1715–1724.
|
| [38] |
Trivedi R, Dai H J, Wang YC, Song L. Know-Evolve: Deep temporal reasoning for dynamic knowledge graphs. In: Proc. of the 34th Int’l Conf. on Machine Learning. Sydney: JMLR, 2017. 3462–3471.
|
| [39] |
Leblay J, Chekol MW. Deriving validity time in knowledge graph. In: Proc. of the 2018 Companion Proc. of Web Conf. Lyon: Int’l World Wide Web Conferences Steering Committee, 2018. 1771–1776. [doi: 10.1145/3184558.3191639]
|
| [40] |
García-Durán A, Dumančić S, Niepert M. Learning sequence encoders for temporal knowledge graph completion. In: Proc. of the 2018 Conf. on Empirical Methods in Natural Language Processing. Brussels: ACL, 2018. 4816–4821. [doi: 10.18653/v1/D18-1516]
|
| [41] |
Dasgupta SS, Ray SN, Talukdar P. HyTE: Hyperplane-based temporally aware knowledge graph embedding. In: Proc. of the 2018 Conf. on Empirical Methods in Natural Language Processing. Brussels: ACL, 2018. 2001–2011. [doi: 10.18653/v1/D18-1225]
|
| [42] |
Goel R, Kazemi SM, Brubaker M, Poupart P. Diachronic embedding for temporal knowledge graph completion. Proc. of the AAAI Conf. on Artificial Intelligence, 34(4): 3988–3995. [doi: 10.1609/aaai.v34i04.5815]
|
| [43] |
Xu CJ, Nayyeri M, Alkhoury F, Yazdi H, Lehmann J. Temporal knowledge graph completion based on time series Gaussian embedding. In: Proc. of the 19th Int’l Semantic Web Conf. on the Semantic Web. Athens: Springer, 2020. 654–671. [doi: 10.1007/978-3-030-62419-4_37]
|
| [44] |
Tian MX, Shou LD, Chen K, Jiang DW, Chen G. A knowledge representation method based on entity time sensitivity. Software Engineering, 2020, 23(1): 1-6(in Chinese with English abstract).
[doi:10.19644/j.cnki.issn2096-1472.2020.01.001] |
| [45] |
Lacroix T, Obozinski G, Usunier N. Tensor decompositions for temporal knowledge base completion. In: Proc. of the 8th Int’l Conf. on Learning Representations. Addis Ababa: ICLR, 2020.
|
| [46] |
Jin W, Qu M, Jin XS, Ren X. Recurrent event network: Autoregressive structure inferenceover temporal knowledge graphs. In: Proc. of the 2020 Conf. on Empirical Methods in Natural Language Processing. ACL, 2020. 6669–6683. [doi: 10.18653/v1/2020.emnlp-main.541]
|
| [47] |
Jain P, Rathi S, Mausam, Chakrabarti S. Temporal knowledge base completion: New algorithms and evaluation protocols. In: Proc. of the 2020 Conf. on Empirical Methods in Natural Language Processing. ACL, 2020. 3733–3747. [doi: 10.18653/v1/2020.emnlp-main.305]
|
| [48] |
Han Z, Chen P, Ma YP, Tresp V. DyERNIE: Dynamic evolution of Riemannian manifold embeddings for temporal knowledge graph completion. In: Proc. of the 2020 Conf. on Empirical Methods in Natural Language Processing. ACL, 2020. 7301–7316. [doi: 10.18653/v1/2020.emnlp-main.593]
|
| [49] |
Wu JP, Cao M, Cheung JCK, Hamilton WL. TeMP: Temporal message passing for temporal knowledge graph completion. In: Proc. of the 2020 Conf. on Empirical Methods in Natural Language Processing. ACL, 2020. 5730–5746. [doi: 10.18653/v1/2020.emnlp-main.462]
|
| [50] |
Han Z, Ma YP, Wang YY, Günnemann S, Tresp V. Graph Hawkes neural network for forecasting on temporal knowledge graphs. In: Proc. of the 2020 Conf. on Automated Knowledge Base Construction. AKBC, 2020. [doi: 10.24432/C50018]
|
| [51] |
Sadeghian A, Armandpour M, Colas A, Wang DZ. ChronoR: Rotation based temporal knowledge graph embedding. Proc. of the AAAI Conf. on Artificial Intelligence, 35(7): 6471–6479. [doi: 10.1609/aaai.v35i7.16802]
|
| [52] |
Zhu CC, Chen MH, Fan CJ, Cheng GQ, Zhang Y. Learning from history: Modeling temporal knowledge graphs with sequential copy-generation networks. Proc. of the AAAI Conf. on Artificial Intelligence, 2021, 35(5): 4732–4740. [doi: 10.1609/aaai.v35i5.16604]
|
| [53] |
Han Z, Chen P, Ma YP, Tresp V. Explainable subgraph reasoning for forecasting on temporal knowledge graphs. In: Proc. of the 9th Int’l Conf. on Learning Representations. ICLR, 2021.
|
| [54] |
Li ZX, Jin XL, Li W, Guan SP, Guo JF, Shen HW, Wang YZ, Cheng XQ. Temporal knowledge graph reasoning based on evolutional representation learning. In: Proc. of the 44th Int’l ACM SIGIR Conf. on Research and Development in Information Retrieval. ACM, 2021. 408–417. [doi: 10.1145/3404835.3462963]
|
| [55] |
Wu JP, Xu YS, Zhang YX, Ma C, Coates M, Cheung JCK. TIE: A framework for embedding-based incremental temporal knowledge graph completion. In: Proc. of the 44th Int’l ACM SIGIR Conf. on Research and Development in Information Retrieval. ACM, 2021. 428–437. [doi: 10.1145/3404835.3462961]
|
| [56] |
Li ZX, Jin XL, Guan SP, Li W, Guo JF, Wang YZ, Cheng XQ. Search from history and reason for future: Two-stage reasoning on temporal knowledge graphs. In: Proc. of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th Int’l Joint Conf. on Natural Language Processing. ACL, 2021. 4732–4743. [doi: 10.18653/v1/2021.acl-long.365]
|
| [57] |
Sun HH, Zhong JL, Ma YP, Han Z, He K. TimeTraveler: Reinforcement learning for temporal knowledge graph forecasting. In: Proc. of the 2021 Conf. on Empirical Methods in Natural Language Processing. Punta Cana: ACL, 2021. 8306–8319. [doi: 10.18653/v1/2021.emnlp- main.655]
|
| [58] |
Park N, Liu FC, Mehta P, Cristofor D, Faloutsos C, Dong YX. EvoKG: Jointly modeling event time and network structure for reasoning over temporal knowledge graphs. In: Proc. of the 15th ACM Int’l Conf. on Web Search and Data Mining. ACM, 2022. 794–803. [doi: 10.1145/3488560.3498451]
|
| [59] |
Messner J, Abboud R, Ceylan II. Temporal knowledge graph completion using box embeddings. Proc. of the AAAI Conf. on Artificial Intelligence, 36(7): 7779–7787. [doi: 10.1609/aaai.v36i7.20746]
|
| [60] |
Li ZX, Guan SP, Jin XL, Peng WH, Lyu Y, Zhu Y, Bai L, Li W, Guo JF, Cheng XQ. Complex evolutional pattern learning for temporal knowledge graph reasoning. In: Proc. of the 60th Annual Meeting of the Association for Computational Linguistics. Dublin: ACL, 2022. 290–296. [doi: 10.18653/v1/2022.acl-short.32]
|
| [61] |
Zhang JS, Liang S, Sheng YP, Shao J. Temporal knowledge graph representation learning with local and global evolutions. Knowledge-based Systems, 2022, 251: 109234.
[doi:10.1016/j.knosys.2022.109234] |
| [62] |
Zhang FW, Zhang Z, Ao X, Zhuang FZ, Xu YJ, He Q. Along the time: Timeline-traced embedding for temporal knowledge graph completion. In: Proc. of the 31st ACM Int’l Conf. on Information & Knowledge Management. Atlanta: ACM, 2022. 2529–2538. [doi: 10.1145/3511808.3557233]
|
| [63] |
Liu KZ, Zhao F, Chen HX, Li YC, Xu GD, Jin H. DA-Net: Distributed attention network for temporal knowledge graph reasoning. In: Proc. of the 31st ACM Int’l Conf. on Information & Knowledge Management. Atlanta: ACM, 2022. 1289–1298. [doi: 10.1145/3511808.3557280]
|
| [64] |
Xia YW, Zhang MQ, Liu Q, Wu S, Zhang XY. MetaTKG: Learning evolutionary meta-knowledge for temporal knowledge graph reasoning. In: Proc. of the 2022 Conf. on Empirical Methods in Natural Language Processing. Abu Dhabi: ACL, 2022. 7230–7240. [doi: 10.18653/v1/2022.emnlp-main.487]
|
| [65] |
Xu Y, Ou JJ, Xu H, Fu LY. Temporal knowledge graph reasoning with historical contrastive learning. Proc. of the AAAI Conf. on Artificial Intelligence, 37(4): 4765–4773. [doi: 10.1609/aaai.v37i4.25601]
|
| [66] |
Zhang MQ, Xia YW, Liu Q, Wu S, Wang L. Learning long- and short-term representations for temporal knowledge graph reasoning. In: Proc. of the 2023 ACM Web Conf. Austin: ACM, 2023. 2412–2422. [doi: 10.1145/3543507.3583242]
|
| [67] |
Nickel M, Kiela D. Poincaré embeddings for learning hierarchical representations. In: Proc. of the 31st Int’l Conf. on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017. 6341–6350.
|
| [68] |
Abboud R, Ceylan II, Lukasiewicz T, Salvatori T. BoxE: A box embedding model for knowledge base completion. In: Proc. of the 34th Int’l Conf. on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2020. 809.
|
| [69] |
Jin J, Wan HY, Lin YF. Knowledge graph representation learning fused with entity category information. Computer Engineering, 2021, 47(4): 77-83(in Chinese with English abstract).
[doi:10.19678/j.issn.1000-3428.0057353] |
| [70] |
Kullback S, Leibler RA. On information and sufficiency. The Annals of Mathematical Statistics, 1951, 22(1): 79-86.
[doi:10.1214/aoms/1177729694] |
| [71] |
Evans JSBT. Heuristic and analytic processes in reasoning. British Journal of Psychology, 1984, 75(4): 451-468.
[doi:10.1111/j.2044-8295.1984.tb01915.x] |
| [72] |
Evans JSBT. In two minds: Dual-process accounts of reasoning. Trends in Cognitive Sciences, 2003, 7(10): 454-459.
[doi:10.1016/j.tics.2003.08.012] |
| [73] |
Evans JSBT. Dual-processing accounts of reasoning, judgment, and social cognition. Annual Review of Psychology, 2008, 59: 255-278.
[doi:10.1146/annurev.psych.59.103006.093629] |
| [74] |
Sloman SA. The empirical case for two systems of reasoning. Psychological Bulletin, 1996, 119(1): 3-22.
[doi:10.1037/0033-2909.119.1.3] |
| [75] |
Glorot X, Bordes A, Bengio Y. Deep sparse rectifier neural networks. In: Proc. of the 14th Int’l Conf. on Artificial Intelligence and Statistics. Fort Lauderdale: AISTATS, 2011. 315–323.
|
| [76] |
Afrassa KW, Cosgun G, Gursoy UF, Yildiz EM, Aktaş MS. On the community discovery methods for complex networks: A case study. In: Proc. of the 2020 Federated Conf. on Computer Science and Information Systems. Sofia: FedCSIS, 2020. 473–477. [doi: 10.15439/2020F88]
|
| [77] |
Rossetti G, Guidotti R, Pennacchioli D, Pedreschi D, Giannotti F. Interaction prediction in dynamic networks exploiting community discovery. In: Proc. of the 2015 IEEE/ACM Int’l Conf. on Advances in Social Networks Analysis and Mining. Paris: ACM, 2015. 553–558. [doi: 10.1145/2808797.2809401]
|
| [78] |
Liu HH, Yang YD, Wang XC. Overcoming catastrophic forgetting in graph neural networks. Proc. of the AAAI Conf. on Artificial Intelligence, 35(10): 8653–8661. [doi: 10.1609/aaai.v35i10.17049]
|
| [79] |
Suchanek FM, Kasneci G, Weikum G. Yago: A core of semantic knowledge. In: Proc. of the 16th Int’l Conf. on World Wide Web. Banff: ACM, 2007. 697–706. [doi: 10.1145/1242572.1242667]
|
| [80] |
Nickel M, Tresp V, Kriegel HP. Factorizing YAGO: Scalable machine learning for linked data. In: Proc. of the 21st Int’l Conf. on World Wide Web. Lyon: ACM, 2012. 271–280. [doi: 10.1145/2187836.2187874]
|
| [81] |
Vrandečć D, Krötzsch. Wikidata: A free collaborative knowledgebase. Communications of the ACM, 2014, 57(10): 78-85.
[doi:10.1145/2629489] |
| [2] |
王萌, 王昊奋, 李博涵, 赵翔, 王鑫. 新一代知识图谱关键技术综述. 计算机研究与发展, 2022, 59(9): 1947-1965.
[doi:10.7544/issn1000-1239.20210829] |
| [6] |
刘峤, 李杨, 段宏, 刘瑶, 秦志光. 知识图谱构建技术综述. 计算机研究与发展, 2016, 53(3): 582-600.
[doi:10.7544/issn1000-1239.2016.20148228] |
| [9] |
徐涌鑫, 赵俊峰, 王亚沙, 谢冰, 杨恺. 时序知识图谱表示学习. 计算机科学, 2022, 49(9): 162-171.
[doi:10.11896/jsjkx.220500204] |
| [10] |
张义杰, 李培峰, 朱巧明. 基于自注意力机制的事件时序关系分类方法. 计算机科学, 2019, 46(8): 244-248.
[doi:10.11896/j.issn.1002-137X.2019.08.040] |
| [44] |
田满鑫, 寿黎但, 陈珂, 江大伟, 陈刚. 一种基于实体时间敏感度的知识表示方法. 软件工程, 2020, 23(1): 1-6.
[doi:10.19644/j.cnki.issn2096-1472.2020.01.001] |
| [69] |
金婧, 万怀宇, 林友芳. 融合实体类别信息的知识图谱表示学习. 计算机工程, 2021, 47(4): 77-83.
[doi:10.19678/j.issn.1000-3428.0057353] |
 2024, Vol. 35
2024, Vol. 35


