面向链接预测的知识图谱表示学习方法综述
杜雪盈
,
刘名威
,
沈立炜
,
彭鑫
软件学报  2023, Vol. 35 2023, Vol. 35 Issue (1): 87-117 Issue (1): 87-117 |
近年来, 云计算、移动互联网、物联网等信息技术的迅猛发展, 引发了网络数据爆炸式增长. 大数据时代的到来推动了以专家知识为核心的知识工程向以数据驱动为核心的大数据知识工程的转变[1]. 知识图谱 (knowledge graph, KG) 正是这一新型知识工程的典型代表. 知识图谱是以图的形式表现客观世界中的实体及其之间关系的知识库[2], 由实体和关系组成. 实体作为图节点, 表示真实世界中的物体或抽象的概念; 关系作为图边, 表示实体之间的联系. 作为直观的结构化知识表达方式, 知识图谱能够从海量数据源中抽取并存储丰富的知识, 并通过知识表示与推理技术将可处理的先验知识提供给智能系统, 提升系统的认知智能. 因此, 知识图谱被广泛应用于信息检索[3-5]、问答系统[6-10]和推荐系统[11-13]等众多应用领域.
目前, 较为常用的知识图谱有 FreeBase[14]、Wikidata[2]、DBpedia[15]、Yago[16], 以及 Google Knowledge Graph[17]等, 然而这些知识图谱都存在不同程度的信息缺失. 以 FreeBase[14]为例, 70%的人物实体缺失出生地信息, 99%的人物实体缺失种族信息[18,19]. 为解决知识图谱构建欠完整性问题, 实现知识图谱自动补全, 需要借助表示学习 (representation learning, RL) 与链接预测 (link prediction, LP)[20]. 由于实体和关系在知识图谱中往往以符号化的形式表示, 因此要利用目前先进的深度学习技术来发现海量实体之间的隐藏关系, 就需要将实体和关系转换为数值形式的表示[21]. 这一过程正是表示学习, 即从原始知识图谱中自动学习出每个节点和边的有效特征, 并以低维向量的形式实现对实体和关系语义的表示[22]. 链接预测作为隐关系发现的重要任务, 也称链路预测. 目前较为先进的模型大多都选择在表示学习的基础上, 通过知识图谱中已有的事实知识预测缺失的实体与关系[23]. 一方面, 知识图谱表示学习通过不同的建模方式学习实体和关系的向量表示, 从而利用数值计算更好地预测缺失链接; 另一方面, 链接预测是表示学习的直接应用, 其准确性经常被用做表示学习方法的评测指标, 因此二者有着不可分割的关系.
本文将从知识表示形式、表示学习建模方式两个维度对面向链接预测的知识图谱表示学习方法研究进展进行论述. 图1按照时间顺序列出了本文所综述的3种知识表示形式下4类表示学习方法的主要模型, 具体包括了从2012–2021年这10年内提出的35种表示学习模型. 此外, 图1中还展示了不同模型之间的演化关联与每个模型所涉及的优化方式.
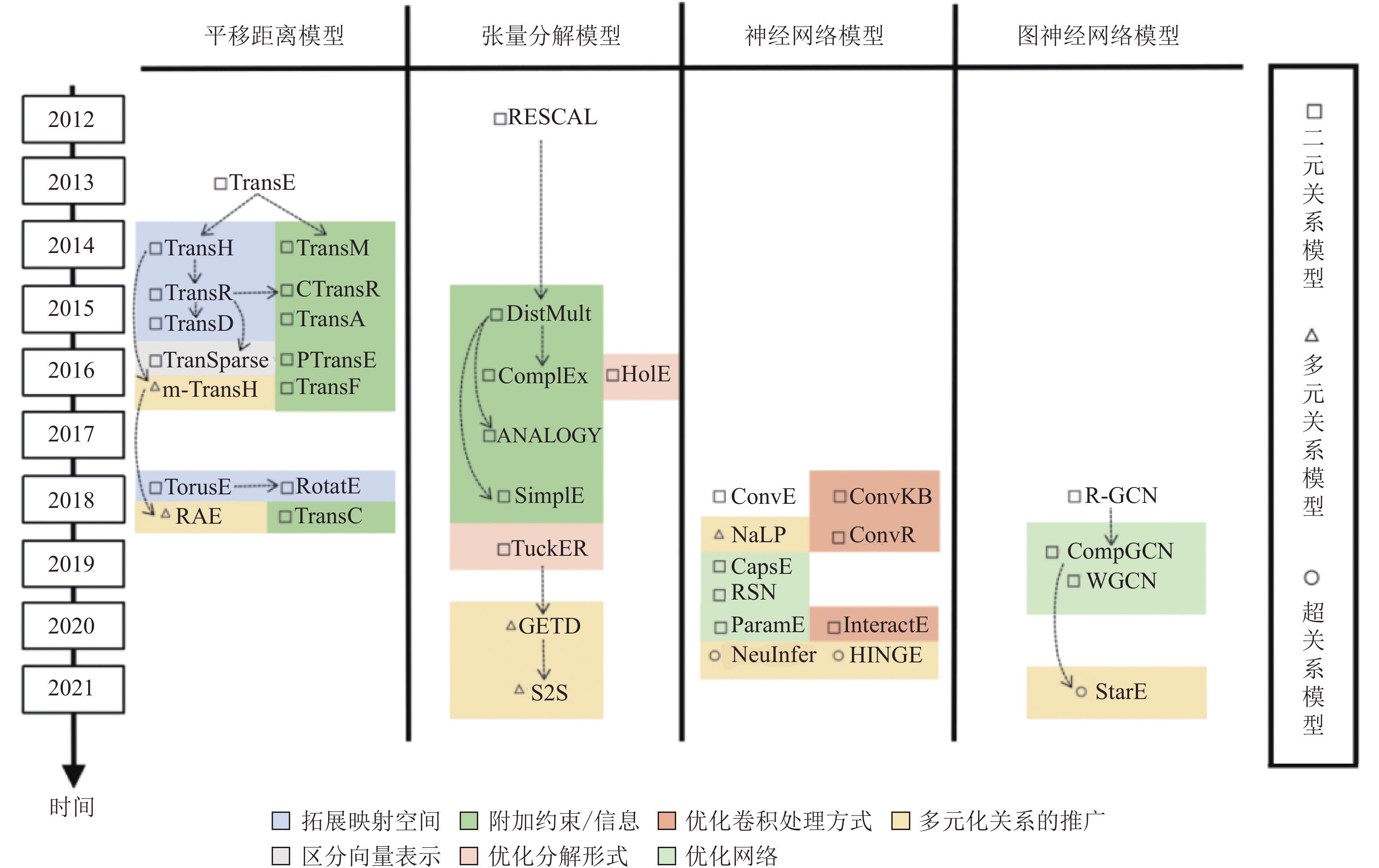
|
图 1 知识图谱表示学习技术划分框架 |
目前, 基于各种知识表示形式的表示学习方法均开展了研究, 但现有综述主要聚焦于二元关系的知识表示学习, 且对于图神经网络模型的介绍不够充分. 基于此, 本文详细整理总结了4种面向链接预测的表示学习方法在知识图谱关系多元化发展趋势下的演化历程及其未来研究方向. 具体地, 本文第1节主要介绍目前知识图谱表示学习方法的背景与相关工作. 第2节主要介绍链接预测任务的目标与问题的基本解决流程, 并对二元关系、多元关系和超关系下的链接预测问题进行了数学建模. 在此基础上, 第3节和第4节具体综述平移距离、张量分解、传统神经网络和图神经网络这4类算法在不同知识表示形式下的设计思路、代表模型及其发展过程. 第5节介绍链接预测实验常用的数据集和评估指标, 并基于此给出了上述模型的实验结果和对比分析. 第6节讨论该领域目前遇到的一些挑战与未来可能的发展方向, 最后总结全文.
1 知识图谱表示学习背景及相关工作知识图谱表示学习的研究可以从知识表示形式、表示学习建模方式两个维度进行讨论.
从知识表示形式的角度看, 面向链接预测的表示学习研究可以被细分为3个方向: 基于二元关系 (binary relations)、基于多元关系 (N-ary relations) 和基于超关系 (hyper-relations) 的研究 (详细定义见第 2.2 节).
早期的知识表示主要基于二元关系, 即利用三元组
二元关系虽然简单通用、使用方便, 但也存在表现力不足、难以表示复杂知识的问题. 复杂知识中包含多个关系和3个及以上的实体, 若将此类知识拆分为多个三元组, 将导致大量语义关联信息在构建知识模型时丢失, 从而影响后续表示学习与链接预测效果. 为解决这一问题, 多元关系表示形式与超关系表示形式应运而生. Wen等人[24]和Rosso等人[25]分别在2016年和2020年提出基于多元关系和超关系的链接预测方法. 多元化的知识表示形式通过更准确的知识表示与更全面的信息覆盖, 显著提高了链接预测的准确率.
基于上述, 这3种知识表示形式并非相互独立, 而是逐步递进的关系. 如何将现有面向链接预测的知识表示学习算法扩展到多元化关系上成为当前该领域的重要研究内容.
从表示学习建模方式的角度看, 面向链接预测的知识表示学习技术可以被细分为4类模型: 平移距离模型、张量分解模型、传统神经网络模型和图神经网络模型 (详细定义见第3节).
从整体上看, 前两者针对知识表示形式与链接预测任务进行了基于明确语义的数学建模, 因此具有强解释性. 神经网络模型是传统神经网络在知识图谱领域的应用模型, 虽然可解释性较差, 但在不同知识表示形式更易泛化与推广, 且更易与其他知识表示学习方法结合, 以提升模型性能; 图神经网络模型借助其强大的图数据表示能力与局部结构建模能力, 一经提出立刻在图表示学习领域展示出惊人的潜力, 近年来被越来越多地用于链接预测任务. 从具体实现方式上看, 前三者的表示学习与预测过程通过同一评分函数
目前, 基于各种知识表示形式的表示学习方法均开展了研究, 但现有综述主要聚焦于二元关系的知识表示学习. 文献[26]从知识推理的角度出发, 概述了面向知识图谱的知识推理研究进展. 虽然涉及部分二元关系知识表示学习模型在知识推理中的应用, 但文章花费大量篇幅介绍基于逻辑与规则的传统推理方法与知识推理应用, 缺少对表示学习技术细节的展示. 文献[27,28]重点综述了知识图谱嵌入方法, 文献[28]相较于文献[27]更加全面, 并且着重分析了基于路径和图神经网络的模型, 但他们缺少多元化知识表示形式下知识嵌入的模型. 文献[22,23]对近年来面向知识图谱链接预测的表示学习模型进行了较为全面的综述, 但文章同样侧重于二元关系下的模型, 并且缺少基于图神经网络的知识表示学习模型介绍. 文献[20]从知识的表示、构建与推理几个方面对知识图谱进行了较完整的综述. 文章虽然提到了多元化关系下的图谱表示与推理, 但主要从知识超图的角度对其进行分析, 未对多元关系与超关系进行区分, 并且相关内容介绍也较为简略.
2 链接预测任务概述与建模本节主要对链接预测这一目标任务进行了系统概述, 同时针对不同的知识表示形式, 将与之对应的链接预测任务进行数学建模.
2.1 链接预测任务概述链接预测即利用知识图谱中已有的事实知识对图谱中缺失的实体或关系进行预测, 具体包括实体预测和关系预测. 如图2所示, 实体预测即预测一条知识中缺失的头实体或尾实体类型; 关系预测即预测一条知识中缺失的关系类型.
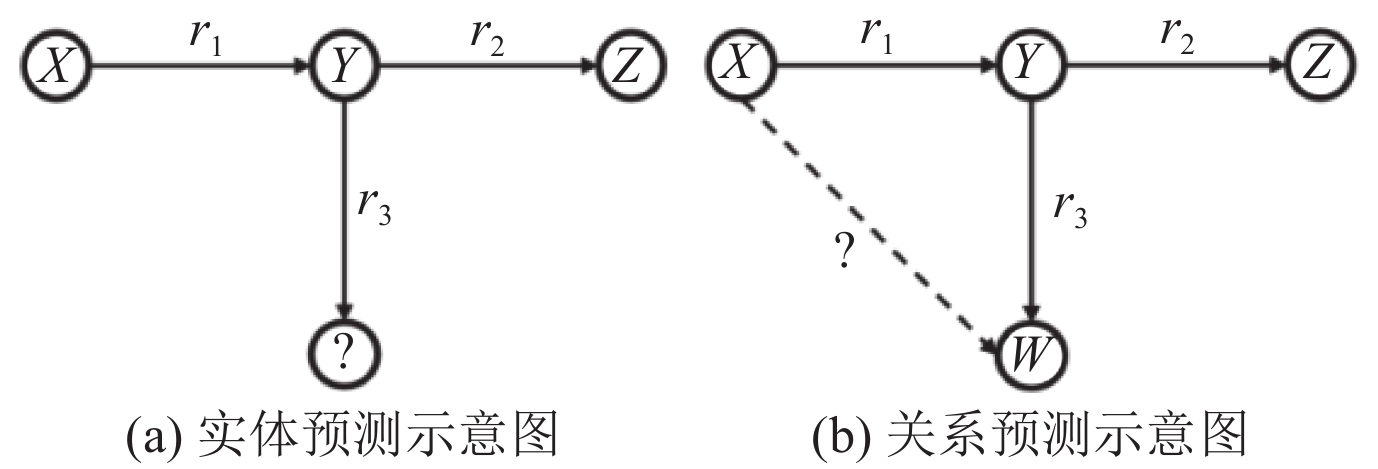
|
图 2 链接预测示意图 |
在实现链接预测任务时, 基于传统表示学习的链接预测(包括基于平移距离模型、张量分解模型和传统神经网络模型的链接预测)和基于图神经网络的链接预测有所区别.
传统链接预测的实现流程可以分为表示学习和预测两部分. 链接预测模型通常会定义一个评分函数
在表示学习过程中, 实体和关系的低维向量表示根据优化目标进行学习. 其优化目标即最大化所有正确样本评分函数得分的同时, 最小化错误样本的评分函数得分. 模型的实体嵌入向量和关系嵌入向量表示可以随机初始化, 也可以利用预训练模型进行初始化, 之后基于目标函数通过不同的优化算法调整改进. 如果模型中包含除了实体和关系向量表示外的其他参数(如神经网络模型中的权值
在预测过程中, 模型将数据集中存在的所有实体或关系依次填补进待预测的知识空缺位置中, 以评分函数作为评测指标, 计算每个实体或关系作为正确缺失信息的可能性得分. 候选实体或关系的得分越高, 其作为链接预测的目标实体或关系的可能性越大. 在整个过程中, 知识嵌入的表示学习过程与预测过程共用同一个评分函数
不同于传统链接预测, 在基于图神经网络的链接预测中, 知识表示学习过程和预测过程相对独立. 目前的图神经网络模型均以编码-解码的结构进行预测. 编码过程对应于知识表示学习部分, 解码过程对应于预测部分, 两部分可以分开进行. 在利用不同的图神经网络进行知识图谱的图表示学习之后, 模型既可以使用传统链接预测方法中已经提出的评分函数作为预测指标, 也可以利用现有的其他领域模型作为解码器, 根据编码阶段学习好的知识向量表示, 再进行评测模型的学习和预测. 因此, 基于图神经网络的知识表示模型的提出不一定针对链接预测任务, 但由于图神经网络的先进性, 基于此类模型进行的链接预测效果十分显著.
2.2 链接预测任务建模通常, 知识图谱领域下的知识库被构建为

|
图 3 不同知识表示形式对比示意图 |
(1) 基于二元关系的链接预测
三元组是知识图谱中最常见的知识表示单元, 通常被分解为(头实体, 关系, 尾实体), 分别对应一条知识描述的(主语, 谓语, 宾语). 本文用
(2) 基于多元关系的链接预测
为更好地描述包含多个实体和关系的事实知识, 多元关系知识表示形式被提出. 多元关系表示用一组角色-键值对(role-value pairs)描述事实知识, 其中, 角色
(3) 基于超关系的链接预测
多元关系的表示形式虽然一定程度上保留了多个实体与关系的关联信息, 但缺点也较为明显. 一方面, 这种表示形式彻底破坏了三元组的表示结构; 另一方面, 所有的关系与实体以角色-键值对的形式被平行存储, 缺少主次关系的体现. 实际上, 每条知识都有其主干描述信息, 这意味着对于多元知识, 也应该存在一个主三元组存储主干信息, 其余的附加实体与附加关系都应该是这一主三元组的辅助描述信息. 在知识图谱中, RDF*图[29]和标记属性图LPG[30]均通过限定词键值对的形式将实体-关系对附加到主三元组中, 以进一步细化每条知识. 在知识图谱Wikidata中, 多元关系知识正是通过该方式表示; 从2018年开始, DBpedia的新版本也包含了与Wikidata类似的超关系知识; 此后, YAGO 4[31]也采用了RDF*的知识编码.
基于此, 为进一步提高多元关系知识表示的准确性, 同时更好适应现有知识图谱的存储形式, 超关系的知识表示形式被提出. 超关系表示保留了三元组的结构, 将每条知识分解为一个主三元组
此外, 还有部分研究者将超图(hypergraph)的研究应用于知识表示领域[32-34]. 超图是一种特殊的图, 图中每条边可以连接多个节点, 超图的边也被称为超边. 在知识超图的表示形式下, 每条多元化知识中的全部实体节点被一条关系超边相连. 但这种结构在进行知识表示时存在明显弊端: 由于所有信息被不分主次地包含在一条知识中, 相比于超关系, 知识超图的表示形式更接近于多元关系, 这意味着知识超图表示也存在多元关系表示的所有缺陷; 此外, 对于包含多个关系的多元知识, 知识超图的表示限制更多. 因此, 知识超图的表示形式目前仍不够成熟, 现阶段还无法较好地应用于链接预测领域.
综上所述, 目前进行知识建模的表示形式主要有二元关系、多元关系和超关系3种. 二元关系(三元组)表示形式最常见, 但其无法描述包含多个实体和关系的事实知识; 多元关系虽然保留了多个实体与关系的关联关系, 但所有的实体与关系以角色-键值对的形式被平行存储, 缺少主次关系的体现; 超关系用一个主三元组存储主干信息, 其余关系与实体用限定词键值对的形式作为辅助信息存储. 因此, 这3类表示形式对知识表示的准确性是依次递增的.
3 面向二元关系链接预测的知识表示学习方法本节主要介绍上述4类知识图谱表示学习方法的建模思路与实现流程, 并面向二元关系链接预测任务概述每类方法代表模型的演化过程与优缺点.
3.1 基于平移距离的知识表示与预测平移距离模型在词向量(Word2Vec)[35]的启发下, 将知识图谱中的实体和关系映射到连续的向量空间, 利用头尾实体和关系的映射向量表达原图中的语义信息和链接关系. 作为最经典的知识图谱表示学习模型, 平移距离模型的出现推动了早期知识图谱表示学习的快速发展, 同时也带动其下游任务——链接预测的共同发展.
TransE模型[36]由Bordes等人于2013年提出. 受到词向量空间平移不变现象的启发, 作者将TransE的语义信息进行如下建模:
| t≈h+r | (1) |
即将三元组
| f(h,t)=|h+r−t|L1/L2 | (2) |
基于TransE模型的表示学习思想和语义建模思路, 该系列衍生出大量表示学习算法, 其主要优化方向有拓展实体关系的映射空间或改进映射方式、区分嵌入向量的表示形式、增加实体关系约束以及增添附加信息(例如权值信息)等. 通过这些优化, 模型应尽可能表达更多的原图语义信息, 同时消除不必要的语义歧义.
(1) 拓展实体关系的映射空间
在平移距离模型的映射空间发展过程中, 代表模型有TransH[37]、TransR[38]和TransD[39]. 其向量转换过程与评分函数沿用TransE构造思想, 并在此基础上对实体和关系进行了映射空间的拓展.
TransH模型[37]的提出旨在改进TransE模型无法处理复杂关系(1-N, N-1和N-N)的缺陷. 由于每个实体和关系在表示学习过程中仅对应特定的单一嵌入向量, 导致TransE模型只能对1-1的关系建模. 平移距离模型中的复杂关系的建模需要模型为每个实体或关系构造不同的向量表示. TransH将关系向量拆分为超平面范数向量
| {h⊥=h−wTrhwrt⊥=t−wTrtwr | (3) |
训练过程中, TransH针对投影到不同超平面上的头实体向量
| fr(h,t)=|hr+r−tr|22 | (4) |
TransR模型[38]将实体空间与关系空间区分开, 以进一步拓展平移距离模型的映射空间. TransH将实体投射到不同超平面后, 原实体空间中相近的实体在超平面中依然距离相近. 但由于关注的属性不同, 相似的实体可能存在完全不同的语义. 例如, 当“苹果”实体作为“水果”解释时, “梨”实体应与之相似; 但当“苹果”实体作为“IT公司”解释时, “梨”实体则与之相去甚远. 为解决这一问题, TransR模型为每个关系
| hr=hMr,tr=tMr | (5) |
TransD模型[39]继续拓展实体关系的映射空间, 在TransR的基础上将头尾实体的投影过程进行区分. 作者指出, 此前的平移距离模型均对三元组中的头尾实体向量进行了相同的映射操作, 然而三元组中的头尾实体可能表示不同的实体类别, 因此模型应该以不同的方式对其进行转换. 基于此, TransD分别构造了
| hr=hMrh,tr=tMrt | (6) |
为更直观地体现映射方式的演进过程, 图4展示了不同模型映射方式的对比图. 从不同超平面, 到不同空间, 再到将头尾实体向量分别映射到不同空间, 平移距离系列模型将实体映射到越来越广的空间区域中. 这一操作虽然显著提高了模型的表达能力和预测准确率, 但也增加了算法的复杂度, 导致部分模型在实际应用中难以用于大规模知识图谱.
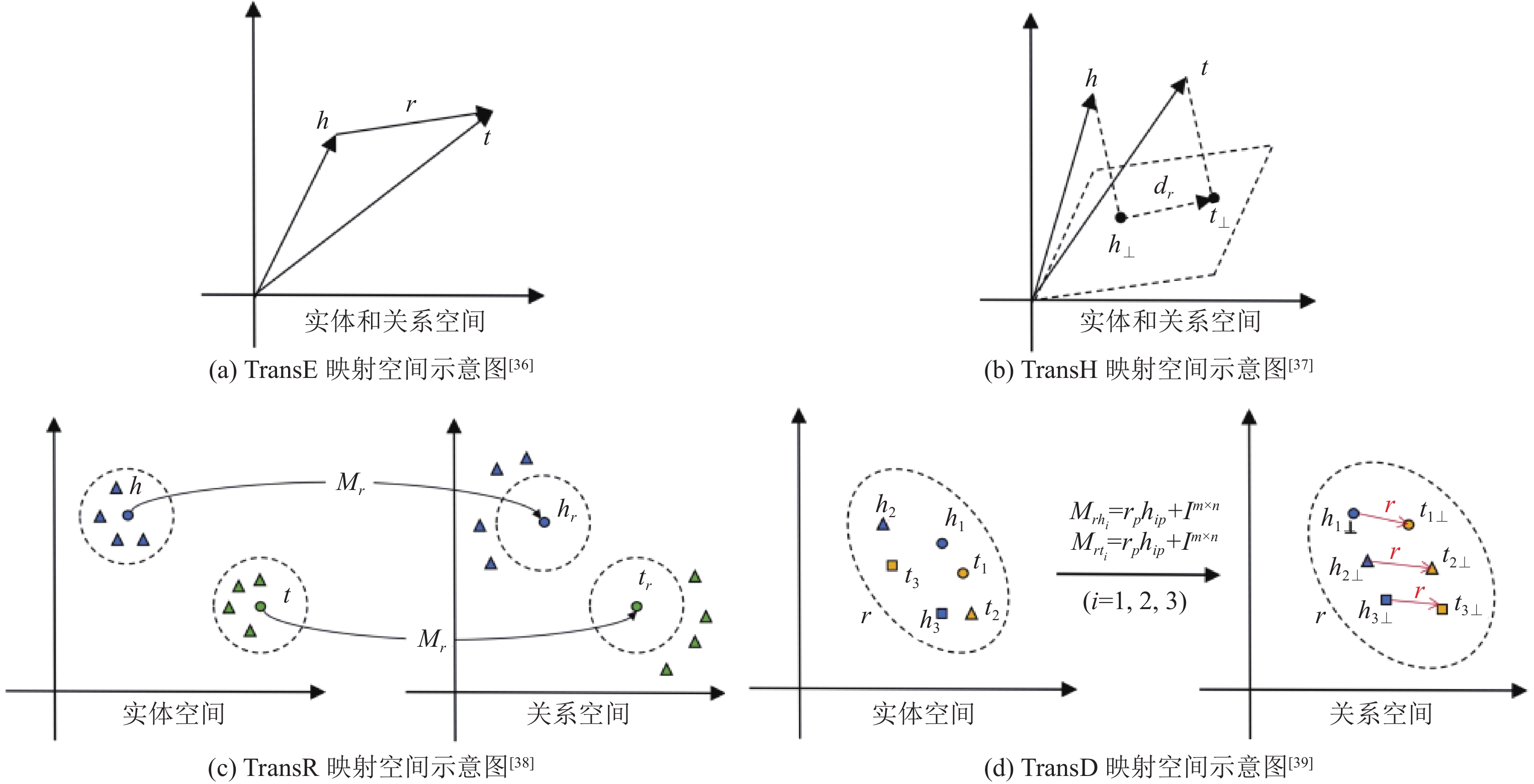
|
图 4 平移距离模型映射方式对比图 |
(2) 改进映射方式
除了拓展实体与关系的映射空间, 模型还可以通过增加旋转操作的方式改进映射方式.
TorusE模型[40]将三元组投影到一个环形曲面(torus)中, 并基于传统平移距离模型的优化目标
| {fL1(h,r,t)=2dL1([h]+[r],[t])fL2(h,r,t)=(2dL2([h]+[r],[t]))2feL2(h,r,t)=(deL2([h]+[r],[t])/2)2 | (7) |
RotatE模型[41]将三元组投影到复数向量空间, 并将关系嵌入定义为旋转矢量, 令三元组的映射操作等价于实体嵌入沿坐标轴旋转的过程, 具体地, 作者定义如下评分函数:
| −|h⊙r−t| | (8) |
其中,
此类旋转约束通过更加有效的空间变换进一步改进知识的向量表示, 显著提高了模型的表达能力. 增加旋转操作后的映射模型示意图如图5所示.
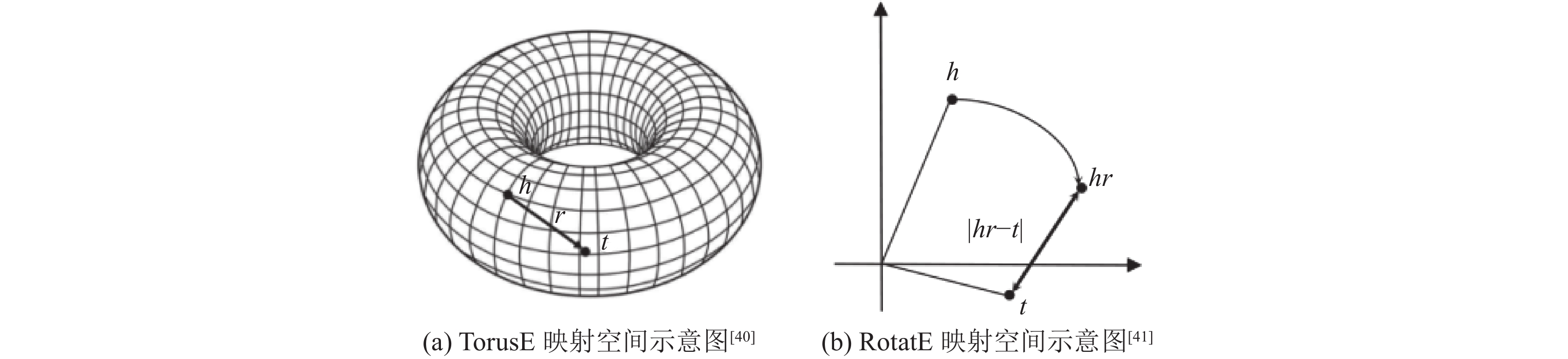
|
图 5 旋转映射模型示意图 |
(3) 区分嵌入向量的表示形式
在映射方式发展的同时, 部分研究人员通过区分不同的关系嵌入向量形式, 进一步优化模型.
在知识图谱中, 实体和关系存在异质性(heterogeneous)和不均衡性(unbalanced)[42], 导致实体在映射的向量空间内分布不均——部分实体之间的关系错综复杂, 部分实体相对孤立, 不同关系相连的头尾实体数量也有较大差异. 上述模型均使用相似的嵌入向量形式表示所有的实体和关系, 这可能导致对复杂关系欠拟合、对简单的关系过拟合的问题.
TranSpare模型[42]为解决这一问题, 提出使用不同稀疏程度的矩阵进行关系嵌入表征的方法进行表示学习. 该模型在TransR的基础上, 使用可变的稀疏矩阵
| θr=1−(1−θmin)Nr/Nr∗ | (9) |
其中,
| hp=Mr(θr)h,tp=Mr(θr)t | (10) |
(4) 增加实体关系约束
除上述优化方式外, 还有部分研究人员通过对实体嵌入和关系嵌入施加额外约束(如组约束和路径约束)或附加信息(如加权等操作)的方式, 进一步帮助本系列模型增强表达能力.
CTransR[38]是TransR的扩展模型. 该模型先将不同的头尾实体对聚类成组, 再学习每个组对应的不同关系向量, 以获取每个关系类型下的实体关联关系.
PTransE[43]利用路径规则作为额外约束对TransE模型进行改进. 通过对多跳关系路径进行建模, PTransE提出了三元组的链式表示, 使得该模型在知识推理领域发挥出显著作用[26].
TransC[44]为加强图谱中概念实体相关的表示能力, 提出了区分概念(concept)和实例(instance)的知识表示学习方法: 将概念用球
| {fe(i,c)=|i−p|22−mfc(ci,cj)=|pi−pj|22+mi−mj | (11) |
其余关系三元组仍采用和TransE相同的评分函数.
TransF[45]为提高模型的泛化能力, 对评分函数中的优化目标进行改进. 不同于TransE要求严格执行
| fr(h,t)=(h+r)Tt+hT(t−r) | (12) |
在实验过程中, Feng等人[45]分别在TransE、TransH和TransR模型中增加了这一约束, 改进后的模型预测结果准确率均有所提升.
TransM[46]通过给每条知识增加权重
| wr=1log(hrptr+trphr) | (13) |
根据
TransA[47]为解决传统模型中正确解集对应的球型等势面灵活性不足问题, 使用马氏距离代替此前平移距离模型中的欧氏距离, 从而得出新的评分函数:
| fr(h,t)=(|h+r−t|)TWr(|h+r−t|) | (14) |
作者利用关系
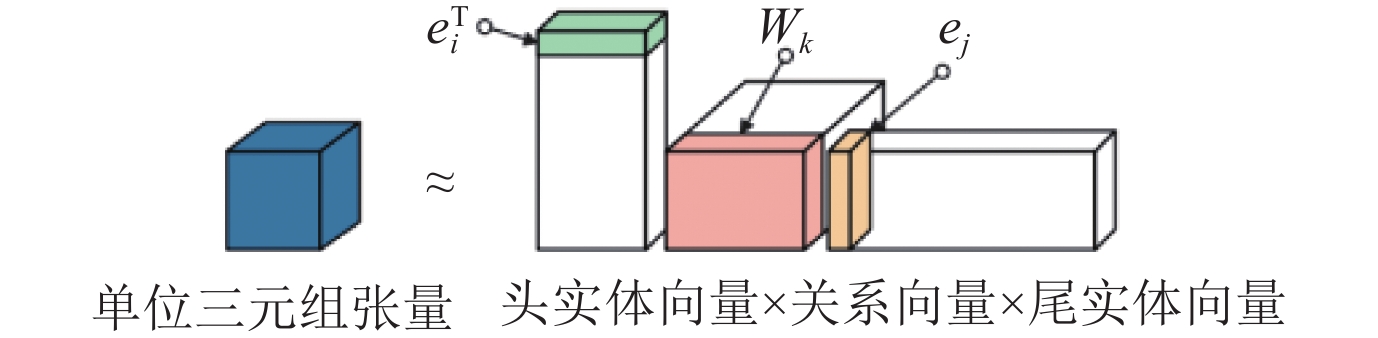
张量分解模型将整个知识图谱看作一个三维邻接矩阵(三阶张量), 矩阵由无数更小的单位三阶张量组成, 每个单位三阶张量代表一个二元关系知识的三元组. 若该事实知识存在, 则该张量对应的元素值为1; 若不存在, 则对应的元素值为0. 张量分解的原理是令每个三元组对应的单位三阶张量分解为3个低维向量的乘积, 3个低维向量分别对应三元组中的头尾实体和关系的表示向量, 乘积尽可能接近原单位张量值(即正确三元组样本接近1, 错误三元组样本接近0). 张量分解示意图如图6所示.

|
图 6 张量分解示意图 |
由于涉及大量头尾实体和关系的矩阵运算, 实体和关系的信息可以进行深层次交互, 这使得张量分解模型具有较强的表现力. 同时张量分解的过程对于头尾实体出现的顺序没有要求, 因此张量分解模型很适合表示对称关系. 此外, 除了TuckER模型, 该系列模型一般不需要使用共享参数[23], 这令其计算复杂度通常较小, 也更容易训练.
RESCAL[48]是最早出现的张量分解表示学习模型. 该模型将头尾实体嵌入向量表示为一维向量, 关系嵌入向量表示为二维向量, 是典型的双线性模型(bilinear models), 其评分函数的定义如下:
| ϕ(h,r,t)=h×r×t | (15) |
其中,
虽然提出了一种全新的表示学习模型, 但RESCAL模型仍存在明显缺陷: (1)以满秩矩阵表示关系向量带来大量的运算, 增加了训练复杂度; (2) RESCAL的评分函数具有交换性, 即
为进一步发展张量分解模型, 大量模型通过施加张量约束或改进分解方式的方法对模型进行了优化.
(1) 施加张量约束
基于RESCAL的建模思想, DistMult[49]、ComplEx[50]、Analogy[51]、SimplE[52]等双线性张量分解模型相继提出. 每个模型都在之前模型的基础上施加了不同的约束, 以提高模型的表达能力. 此类模型的分解方式如图7所示.
|
图 7 双线性张量分解模型示意图 |
DistMult[49]为降低模型复杂度, DistMult要求
ComplEx[50]为进一步解决关系对称问题, 利用尾实体向量的共轭转置向量
ANALOGY[51]通过类比推理的方式优化了张量分解模型. 该模型继续采用双线性评分函数, 并在此基础上改进了DistMult模型对关系嵌入的约束, 在对称矩阵的基础上增加了两个可以实现类比推理结构的约束: (1)
SimplE[52]通过对头尾实体和关系的嵌入向量进行关联扩展的方式, 解决了之前模型的对称性问题. 在继续沿用DistMult中关系嵌入对角矩阵的基础上, SimplE进行了以下改进: (1)将每个实体
| 1/2(hh×r×tt)+1/2(ht×r−1×th) | (16) |
通过这种方式, SimplE不仅对不对称的关系成功建模, 其表达能力也显著提高.
(2) 张量的分解形式
除了上述双线性模型之外, 张量分解模型还可以利用其他分解形式表示知识.
HolE[55]利用实体向量的循环相关性, 成果对三元组交互过程进行压缩, 有效减少了模型参数量. HolE将实体嵌入
| (h∗t)×r | (17) |
由于循环关联运算是完整矩阵乘积运算的压缩, 因此在时间和空间复杂度方面KolE均有明显优势. 此外, HolE在数学上等效于ComplEx, 可以看做ComplEx的泛化情况[56].
TuckER[57]是张量分解模型中唯一涉及共享参数的模型. 该模型依赖于TuckER分解[58], 即将一个知识三元组张量分解为一组向量和一个共享核心张量
| W×1h×2r×3t | (18) |

|
图 8 TuckER分解示意图 |
不同于该系列其他模型含有大量约束条件, TuckER模型中的知识特征主要由共享核
神经网络模型通常将链接预测任务转换为普通的深度学习任务, 根据输入的三元组信息, 利用神经网络学习共享参数(如权重
在早期研究中, 知识图谱表示学习领域代表性的神经网络模型有MLP[18]和SLM[59]等. 随着神经网络的发展, 用于知识表示学习和链接预测的神经网络不再拘泥于单一的神经网络, 越来越多的网络模型逐渐被用于这一领域, 其中应用最广泛的是卷积神经网络(convolutional neural network, CNN)[60], 其优化方向主要在于模型对三元组信息的特征提取过程(卷积方式). 此外, 循环神经网络(recurrent neural network, RNN)[61]、注意力机制(attention mechanism, AM)[62]和胶囊网络(CapsNets)[63]等神经网络模型也被逐渐应用于该领域. 本节主要介绍最新的神经网络模型研究进展.
(1) 卷积神经网络
ConvE[64]是第1个使用多层卷积神经网络解决链接预测任务的模型, 在进行链接预测时, 该卷积神经网络的结构可以被看作一个分类器, 分类的类别个数即该数据集的总实体数
| fr(h,t)=g(W×g([h;r]⊛ω)+b)×t | (19) |
ConvE的网络组成部分包括一个单层的卷积网络, 一个投影层和一个内积层. 该模型将三元组中的实体和关系均表示为一维的嵌入向量, 当计算一条知识的评测得分时, 模型将头实体嵌入向量
尽管开创性地提出二维卷积神经网络模型并将其应用于知识表示学习领域, 但由于只对头实体向量和关系向量进行了卷积操作, ConvE依然难以很好地提取整个三元组的关联特征. 这一缺陷在后续提出的模型中得到了改进.
ConvKB[65]延续了卷积的特征提取操作, 但不同于ConvE仅对头实体向量和关系向量进行卷积操作, ConvKB将三元组中头尾实体和关系对应的嵌入向量同时进行卷积操作, 使得三元组中全部实体关系的特征被一同提取. 在ConvKB中, 实体和关系均被构建为相同大小的一维向量, 头实体向量
ConvR[66]基于卷积神经网络模型进一步对三元组信息的处理进行改进. ConvKB中的一维卷积仅能捕捉向量拼接处的交互关系, ConvE使用的二维卷积虽然比一维卷积获取了更多的交互信息, 但捕捉的交互关系依然有限, 仅限于矩阵堆叠相接行的交互信息. 为进一步挖掘三元组之间的语义信息, 则需要令实体向量与关系向量更充分地进行交互. 基于此, ConvR将关系的嵌入直接作为卷积核, 对头实体的嵌入向量进行卷积, 从而获得头实体与关系完全的交互. 对于任何知识三元组
InteractE[67]同样通过增加实体和关系向量之间的交互对ConvE进行改进. 但不同于ConvR直接将关系嵌入作为卷积核, InteractE主要在向量堆叠过程中进行了优化. 对输入的头实体向量

|
图 9 InteractE向量堆叠方式 |
从上述模型的改进过程中可以看出, 基于卷积神经网络的链接预测模型发展主要体现在不同网络对三元组知识向量的处理方式, 即用于提取三元组特征的卷积操作上. 为了更好地对比不同卷积神经网络模型对三元组的卷积方式, 我们将上述模型的卷积层在图10进行对比展示. InteractE模型同ConvE模型卷积处理相似, 只不过图像堆叠部分采用了图9所示的堆叠方式.

|
图 10 卷积处理对比图 |
(2) 其他神经网络
ParamE[68]直接将神经网络的参数作为关系的嵌入向量
| fr(h,t)=σ(W×fnn([h;r])+b)×t | (20) |
CapsE[69]利用胶囊网络对三元组特征进行编码, 其贡献主要在于首次将胶囊网络的结构引入知识表示学习中. 胶囊网络由被称为胶囊的神经元组组成, 每个胶囊神经元输出一个向量, 层间胶囊的连接通过路由策略进行. 相比于普通神经网络中的神经元只能输出一个具体的值, 胶囊神经元的优势在于其输出的向量可以更好地表示一类模式, 这使得胶囊网络比起普通神经网络有着更好的特征提取能力和泛化能力. CapsE模型在ConvKB的特征提取过程基础上加入两个胶囊层, 进一步捕捉三元组相应维度中的特征, 其评分函数具体定义如下:
| fr(h,t)=|capsnet(g([h,r,t]∗ω))| | (21) |
RSN[70]是首个基于循环神经网络的知识表示学习模型, 作者将循环神经网络与残差学习相结合, 以有效地捕获知识图谱内部和知识图谱之间的长期关系依赖性. 虽然循环神经网络提取局部特征的能力不如卷积神经网络, 但这类模型在知识表示学习与链接预测中, 可以使用多个循环层分析从训练集中提取的全部知识序列, 并以实体-关系链的路径信息存储, 从而对整个知识图谱的关联关系特征有更好的把握. 实现过程中, 作者先使用偏置随机游走对知识图谱的路径进行采样, 之后再利用RSN对关系路径进行建模, 其评分函数具体定义如下:
| σ(rsn(hpr)×t) | (22) |
图神经网络(graph neural network, GNN)[71]是一种专门对图结构数据进行表示学习的神经网络模型. 由于现实生活中大量信息以图数据的形式存在, 如交通网络、社交网络、用户与产品交互信息等, 为更准确和灵活地对这类数据建模, 研究者们将具有强大建模能力的神经网络引入图结构中, 构造了图神经网络. 作为连接主义与符号主义的有机结合产物, GNN不仅使深度学习模型能够应用在图这种非欧几里德结构上, 还为深度学习模型赋予了一定的因果推理能力[72]. 因此, 一经提出, 图神经网络受到了学术界和工业界的广泛关注, 发展迅速. 几年内, 各种图神经网络模型大量涌现, 图卷积网络(graph convolution network, GCN)[73]、图注意力网络(graph attention network, GAT)[74]和图自编码器(graph autoencoder, GAE)[75]等模型被陆续提出. 利用GNN在学习节点表示上的优势, 将其应用于知识图谱领域可以更好地挖掘实体节点之间的深层关联, 提高表示学习准确性, 辅助完成节点分类、链接预测等下游任务, 帮助构建并补全知识图谱.
GNN利用“信息传播”的思想对图数据进行处理. 通过学习映射聚合函数
目前, 已有很多文献对图神经网络领域进行了较为详尽的综述[62, 76, 77], 本节主要以用于知识图谱链接预测的图神经网络模型设计为例, 重点介绍图神经网络在知识图谱表示学习领域上的应用. 由于原始的图神经网络架构只针对节点进行信息聚合, 导致其无法对知识图谱中的关系嵌入进行建模. 因此, 应用于知识图谱领域的图神经网络模型需要针对关系嵌入对其架构进行改进.
| h(k)v=f(∑u∈N(v)W(k)h(k−1)u) | (23) |
R-GCN: Schlichtkrull等人[78]最早开创了利用GCN框架构建知识图谱关系网络的先河, 在2018年提出R-GCN模型. 在编码过程中, 针对每个关系
| h(k)v=f(∑(u,r)∈N(v)W(k)rh(k−1)u) | (24) |
虽然通过关系转换矩阵
CompGCN: Vashishth等人[79]提出了一种用于解决上述问题的模型CompGCN. 首先, CompGCN将图中的关系加入表示学习中, 将关系作为嵌入向量与节点向量进行联合学习. 这意味着在GCN迭代更新时, 节点和关系将一起进行更新. 其次, Vashishth等人设计了一组基向量
| h(k)v=f(∑(u,r)∈N(v)W(k)λ(r)ϕ(h(k−1)u,h(k−1)r)) | (25) |
其中, 组合函数
WGCN: Shang等人[80]提出了带权重的图卷积网络WGCN模型以进一步提高图神经网络编码器的表达能力. 该模型将知识图谱看作多个单一关系的子图, 每个子图只包括一种类型的边. 在信息聚合时, 该模型引入可学习的权重, 该权重由聚合过程中相邻实体节点之间的关系类型决定. 除了对编码器的加权优化, 该作者的另一个贡献是改进了ConvE模型, 为ConvE去掉了向量重组(reshape)步骤, 保留了三元组的语义特性, 并把该模型作为链接预测的解码器, 与WGCN一起拼接为一个端到端的预测模型SACN.
GAT: Velivckovic等人[74]、Nathani等人[81]、Harsha等人[82]将图注意力网络引入知识图谱领域构建出KBGAT模型. GAT也可以理解为加权的GCN网络, 其与WGCN的区别是GAT网络中的关系权重均通过attention网络层计算得出, 而WGCN网络中并未明确介绍其权重的来源. 加权的优化显著增强了模型的表达能力, 在进行关系多元化的推广中也有较强的借鉴意义.
3.5 小 结本节首先介绍了4大类面向链接预测的知识表示学习方法的建模思路与实现流程, 即: 基于平移距离的方法, 基于张量分解的方法, 基于传统神经网络的方法和基于图神经网络的方法, 之后面向二元关系链接预测任务概述了每类方法代表模型的演化过程及其原因.
为针对面向二元关系链接预测的知识表示学习模型进行更直观的对比, 表1总结了上述4类表示学习方法中不同模型的评分函数与各类方法的优化方向及其特点. 如本文第2.1节所述, 基于图神经网络的模型在预测流程上不同于前3种模型, 图神经网络本身仅对应知识表示学习部分, 预测时仍需要借助上述3种模型的评分函数作为预测指标.
| 表 1 模型评分函数与优化方向对照表 |
表1中涉及的运算符号定义如下:
多元化关系的链接预测中包含了多元关系预测与超关系预测. 这两种链接预测的方法均是二元关系下预测方法的推广, 放在一起更加便于对比分析. 因此, 我们将多元关系和超关系的链接预测方法放在同一节进行论述.
同二元关系的链接预测类似, 我们将知识表示学习按照语义建模方式分类, 分为张量分解、平移距离、传统神经网络和图神经网络4类. 本节将重点概述这4类模型进行多元化推广的方式, 以及模型对于多元化关联信息的聚合方法, 并对每个模型的创新点和缺陷进行对比总结.
4.1 基于平移距离的多元化知识表示与预测目前, 基于平移距离的多元化模型有m-TransH[24]和RAE[34], 均基于多元关系表示形式.
m-TransH: Wen等人[24]首次描述了用于链接预测的多元关系规范表示, 搭建出其数学模型, 并率先提出了面向多元关系链接预测的知识表示学习模型m-TransH. 该模型对本文第3.1节所分析的TransH模型进行了多元关系推广, 在沿用TransH映射思想的基础上, 将实体与关系的嵌入向量按照其相对位置信息关联起来, 并组成元关系(meta ralation), 通过超平面范数向量
| fr(t)=|∑ρ∈M(Rr)ar(ρ)Pnr(t(ρ))+br|2,t∈NM(Rr) | (26) |
其中,
虽然元关系结构帮助m-TransH模型完成了多元关系在超平面中的映射, 但这种实体与关系紧密耦合的形式以及严格的位置限制会导致信息丢失的问题. 例如, 在多元关系中, 表示列举的多个实体之间互换位置不会导致整条知识的语义偏差, 但限制其位置关系反而导致误差的产生.
RAE: Zhang等人[34]通过将多层感知器(MLP)引入m-TransH模型的方式, 对m-TransH进行了优化改进, 构建出RAE模型. 该模型利用MLP对实体的相关性进行建模, 并将建模结果耦合进评分函数中, 提高了模型的准确率. 此外, 作者将多元关系的链接预测问题从预测每条知识中的一个缺失实体, 推广到预测每条知识中的一个或多个缺失实体. 基于这一任务需求, 作者提出了实例重构算法. 通过计算不同知识中实体之间的相关性, 算法以基于模式的过滤方式进行实例重构, 从而降低算法复杂度. 基于此, RAE模型构建的损失函数定义如下:
| EI(ΘI,ϕ):=∑r∈R(∑t∈Trfr(t)+∑t−∈T−rReLU(C−fr(t))) | (27) |
由于受到平移距离模型在多元关系中的语义限制, 这两种模型均只能捕捉实体之间的关联性, 导致其进行链接预测时, 只能进行实体预测(键值预测)而不能进行关系预测(角色预测).
4.2 基于张量分解的多元化知识表示与预测目前, 基于张量分解的多元化模型有GETD[83]和S2S[84], 也是基于多元关系的预测模型.
GETD: Liu等人[83]将TuckER推广到多元关系中, 提出了第1个面向多元关系链接预测的张量分解模型GETD, 其示意图如图11所示.

|
图 11 GETD 对 TuckER 的推广示意图[83] |
在N元关系的表示学习中, 该模型先将TuckER模型中的三阶核心张量W重塑为
| ϕ(ir,i1,…,in)=ˆW×1rir×2ei1×3…×n+1ein=TR(1,…,zk)×1rir×2ei1×3…×n+1ein | (28) |
作者通过将该模型与对TuckER模型直接进行
尽管成功将张量分解模型推广到多元关系中, GETD模型依然存在弊端. 由于每条知识的元数直接影响着张量阶数及其分解方式, 因此模型在处理不同元数的知识时必须分别进行分割与训练. 此外, 即便利用张量环对核心张量进行了简化, GETD模型的复杂度仍达到
S2S: Di等人[84]针对上述GETD模型的缺陷进行了改进, 提出了一种全新的张量分解模型S2S. 该模型利用分割嵌入的思想, 将每个实体或关系嵌入分割为N份(N代表该知识库中最高元数的知识), 令不同元数的知识共享不同的嵌入片段, 其示意图如图12(a)所示. 通过这种方式, 该模型可以混合学习不同元数的嵌入向量, 克服了GETD模型必须对不同元数知识分开训练的缺陷. 其评分函数具体定义如下:

|
图 12 S2S 模型示意图[84] |
| fz(s,H;Zns)=∑jr,j1,…,jnZnsk×1rjrir×2…×ns+1ejnsins | (29) |
此外, 文献[84]指出现有知识库中的多元关系数据十分稀疏, 用包含大量参数的密集型的核心张量不仅会导致过参数化的问题, 而且无法对此类数据进行很好的表达. 基于此, S2S模型将稠密的核心张量稀疏化, 将其分解为多个如图12(b)所示的对角矩阵. 模型将稀疏化的核心张量视为随机变量, 建立了一个针对该随机变量的概率分布模型, 利用神经结构搜索算法NAS对不同的多元关系知识进行自动化搜索, 通过不断采样和迭代更新概率分布, 以获取效果最好的稀疏张量分解模型.
4.3 基于神经网络的多元化知识表示与预测由于不受限于明确语义建模, 神经网络模型在多元关系的链接预测中大量涌现, 其网络模型主要基于卷积神经网络. 此外, 超关系的概念也是在进行神经网络建模时提出的, 这是由于带有更明确语义信息的张量分解和平移距离模型目前阶段都难以对这一更灵活知识表示形式进行建模. 本节将对基于多元关系和超关系的神经网络模型分开进行论述.
(1) 多元关系下的神经网络模型
NaLP: Guan等人[86]于2019年首次使用神经网络模型对链接预测任务进行多元化推广, 提出了NaLP模型. 该模型利用多元关系的知识表示形式, 将每个N元知识分解为(N+1)个角色-键值对, 并将这些角色-键值对作为嵌入向量传递到卷积层进行特征提取. 特征提取之后模型用FCN网络对全部的关联关系进行建模, 并给每条知识进行评测打分. 为对模型进行进一步优化, Rosso等人[25]2020年又提出了该模型的变体NaLP-fix, 在原模型整体结构不变的基础上增添了一种负采样策略, 提高了该模型的性能.
HpyE: Fatemi等人[32]受到SimplE模型的启发, 提出了HSimplE与HypE模型, 为具有不同特性的知识(元数不同的多元关系知识)设计了一组卷积内核, 并对特定位置的实体使用特定的过滤器进行嵌入, 以提高模型的表达能力. 但该操作也导致了该模型存在与GETD模型类似的问题, 即缺乏灵活性, 且只能处理固定元数的知识. 该文献的创新点在于尝试了知识超图的知识表示形式. 虽然该知识表示形式目前仍有较大局限性, 但知识超图依然是知识图谱领域值得研究的重要发展方向, 因此这一尝试仍具有重要意义.
综上所述, 基于多元关系的神经网络模型依然存在较大限制: (1)此类模型存在神经网络模型共有的弊端, 即涉及参数较多、训练难度较大, 以及可解释性较差等问题, 这些问题在推广到多元关系的链接预测后更加显著; (2)模型受到多元关系的知识表示建模所限制, 将知识分解为等价的多个角色-键值对, 在特征提取阶段不分主次地提取全部信息, 对预测结果造成负面影响.
(2) 超关系下的神经网络模型
NeuInfer: Guan等人[87]率先提出用主三元组和附加键值对的形式进行知识表示的思想, 并提出基于该表示形式建模的神经网络模型NeuInfer. 该模型采用FCN卷积模块对知识嵌入进行处理, 分别计算出主三元组拼接向量的有效性得分, 以及主三元组与辅助键值对分别拼接后的兼容性评分, 最后将两项评分加权求和得到最终的评测得分. 该论文并未明确提出“超关系”的概念, 但NeuInfer模型是第1个使用超关系思想对知识进行表示学习的模型.
HINGE: Rosso等人[25]提出的HINGE模型是目前基于多元化关系的神经网络算法中性能最好的模型. 作者在论文中第1次明确提出“超关系”的概念, 并使用卷积神经网络框架对其进行建模. HINGE将N元知识拆分为一个主三元组和(N – 2)个限定词键值对, 分别用三元组的嵌入向量与每对限定词的嵌入向量进行卷积, 形成五元组向量, 再对该五元组向量表示进行最小池化操作, 以此捕捉每条知识中主三元组和其限定词之间的关联关系特征.
虽然保留知识的超关系本质使HINGE模型获得了极佳的准确率, 但也令该模型存在时间复杂度过高的致命缺陷. 主三元组与每个辅助限定词对迭代卷积的操作给该模型带来了巨大的时间复杂度. 此外, HINGE模型必须对所有知识进行顺序训练, 即按照知识的限定词数量升序对所有的知识进行排序. 这一操作进一步增加了模型的时间开销, 导致HINGE模型在大规模知识图谱中的使用变得极为不现实.
为展示不同多元化知识表示形式下神经网络模型对于知识的处理区别, 图13展示了NaLP模型、NeuInfer模型和HINGE模型的特征提取对比示意图.
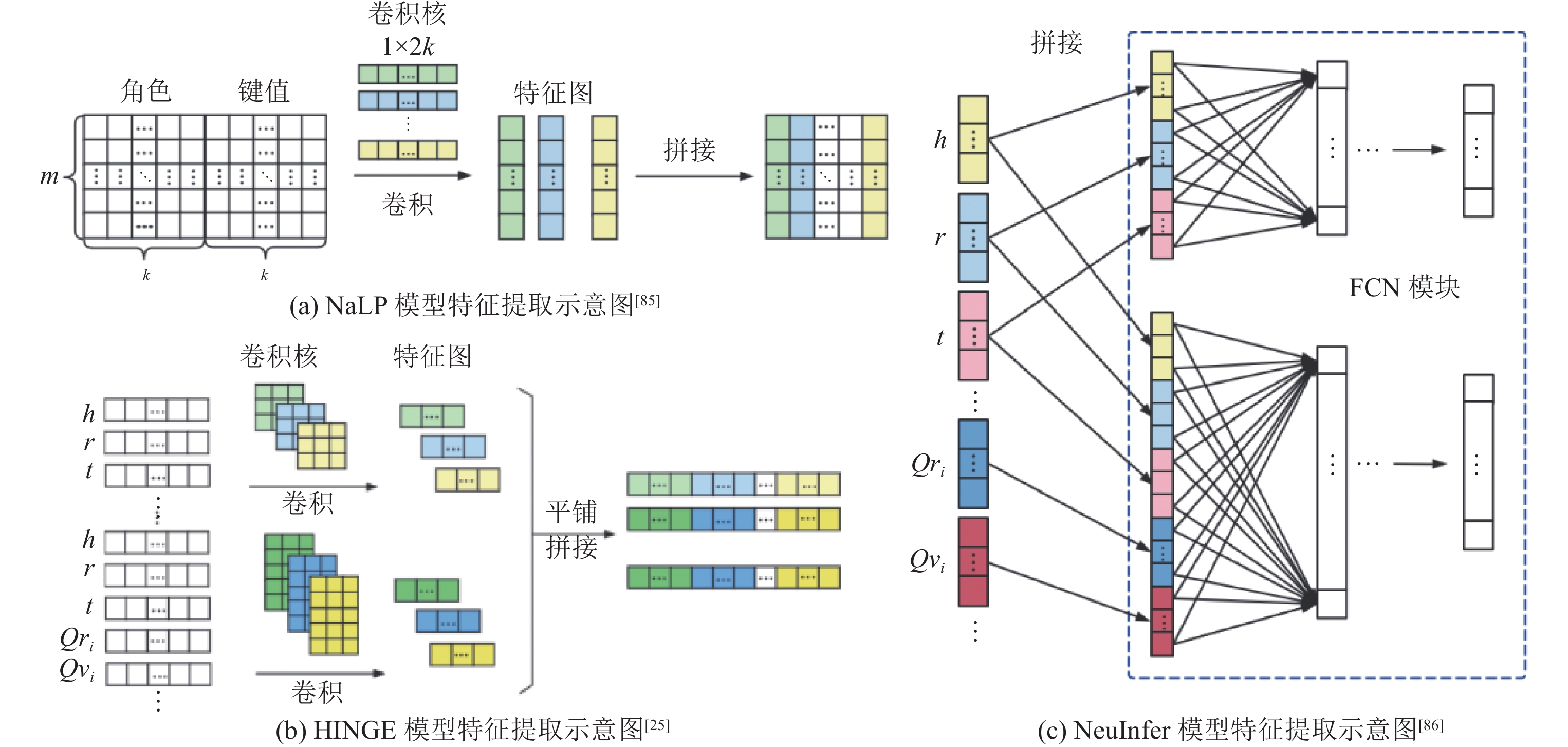
|
图 13 面向多元化关系预测的神经网络特征提取对比图 |
StarE: Galkin等人[88]提出了第1个基于图神经网络进行超关系推广的模型StarE. 同其他用于链接预测的图神经网络模型类似, 该模型以编码-解码结构组成. 编码过程利用图神经网络的消息传递机制, 对超关系知识表示形式进行建模与表示; 解码过程对应预测过程. 在解码器的选择上, 该作者分别选用了ConvE, ConvKB和Transformer这3种模型进行预测, 最终实验效果最好的是StarE+Transformer的组合.
StarE对CompGCN模型进行了超关系下的推广, 将每个代表辅助信息的限定词键值对也进行了嵌入向量表示, 并与主三元组中的实体嵌入和关系嵌入一起进行聚合. 其节点特征向量更新过程如下:
| hv=f(∑(u,r)∈N(v)Wλ(r)ϕr(hu,γ(hr,hq)vu)) | (30) |
实体嵌入与关系嵌入的聚合方式如下:
| γ(hr,hq)=α⊙hr+(1−α)⊙hq | (31) |
其中,
即便仅利用较为基础的图神经网络模型对限定词键值对与主三元组进行了简单的交互, StarE依然获得了当前多元化关系链接预测中最好的实验效果, 这也体现出图神经网络与超关系表示形式在知识表示学习与链接预测任务上的先进性和极大的发展潜力.
4.5 小 结本节主要概述了平移距离、张量分解、传统神经网络和图神经网络4类表示学习方法进行多元化关系推广的方式, 并介绍了面向多元化关系链接预测(具体分为多元关系预测和超关系预测)每类方法的代表模型. 根据上述分析论述, 表2从知识表示形式、模型类别, 创新点和缺陷4方面对面向多元化关系链接预测的知识表示学习方法进行了对比总结.
| 表 2 面向多元化关系链接预测的知识表示学习模型对比 |
结合第3节的内容, 为直观对4类模型的特点进行对比, 表3展示了每类模型的建模思路、优缺点以及进行多元化推广的主要思路.
| 表 3 4类模型对比总结 |
本节对不同知识表示形式下的数据集和3个常用的链接预测效果评测指标进行了介绍, 通过对比不同知识表示学习算法在数据集上的链接预测效果, 详细分析了不同模型的性能与特点.
5.1 数据集对比分析用于链接预测任务的基准数据集通常是对较完善的知识图谱进行采样所得. 数据集内的数据一般被分为训练集、验证集和测试集.
(1) 基于二元关系的数据集
FB15k, WN18, FB15k-237, WN18RR, 以及YAGO3-10[36, 64, 89]是目前较常用于二元关系的链接预测的5个数据集, 数据集中的知识以三元组形式存储. 由于这些数据集已经被诸多文献[23, 54]分析得较为透彻, 本节不再赘述其存储形式, 而重点概述其抽取方式与优缺点.
FB15k由Bordes等人[36]提出. 作者抽取出知识图谱FreeBase中所有被提及次数超过100次, 且存在于维基链接的实体, 之后采集了所有涉及这些实体的知识三元组, 并对所有包含大量数字信息和专有名词的知识进行过滤. 此外, 该数据集将FreeBase中涉及的多元关系转化为多个二元关系组. 如本文第2节所述, 这一转化操作极大程度影响了原始图的结构和语义.
WN18同样由Bordes等人[36]提出. 不同于FB15k来源于通用知识图谱, WN18从领域知识图谱WordNet3中提取所得. 为构建WN18, 作者对WordNet3中较少提及的实体和关系进行过滤, 采集了剩余提及较多的实体和关系. WordNet3是一个语言学知识图谱, 旨在通过提供词典(也称叙词表)支持自然语言处理和自动文本分析的研究. 在WordNet中, 实体对应于同义词集, 关系对应于词汇连接(例如“上义词”). 因此, 该数据集内包含大量实体, 但关系数量较少.
FB15k和WN18是迄今为止最常用于二元关系链接预测的数据集, 但是均存在不同程度的数据泄露问题. 数据泄露指训练集中存在大量测试所用的三元组或测试集三元组的简单逆向三元组, 这使得一个简单用于观察特征的模型、或基于逆向关系检测的反向模型, 都可以在该数据集上轻松达到很好的测试结果. 因此, 知识表示学习模型在这两个数据集上的效果通常较好, 这对于模型性能的评测存在负面影响. 为解决这一问题, 研究人员重新优化提取出FB15k和WN18的子数据集FB15k-237和WN18RR.
FB15k-237是Toutanova等人[53]提出的FB15k子数据集. 作者从FB15k数据集中抽取出237个提及次数最多的关系, 并采集了所有与这些关系相关的知识, 同时删除了训练集中所有与测试集数据等价或存在逆关系的知识. 通过该方式, 作者确保训练集中存在连接关系的实体在验证集和测试集中均不直接连接, 极大程度解决了数据泄露的问题.
WN18RR是Dettmers等人[64]构建的WN18子数据集. 为解决WN18的数据泄露问题, 作者通过类似FB15k-237的过滤方式构建更具挑战性的WN18RR数据集. 但WN18RR数据集存在明显缺陷, 即测试集中存在212个没有出现在训练集中的实体, 导致6.7%的测试知识永远无法被正确预测.
YAGO3-10由Dettmers等人[64]从知识图谱YAGO3[87]中采样所得. 该数据集是包含实体最多的链接预测数据集, 其中三元组主要涉及人的描述属性(例如人的国籍或性别). 作者选择了所有存在10个以上不同关系的实体, 并采集了涉及这些实体的全部知识三元组. 不同于FB15k和FB15k-237, YAGO3-10数据集还保留了知识图谱中关于文本属性的知识. 此外, 逆向模型在YAGO3-10数据集中糟糕的实验结果[63]也证明了该数据集在解决数据泄漏问题的有效性.
为了更直观地对这5个数据集进行对比, 我们将这5个数据集的相关属性列在表4中.
| 表 4 二元关系数据集属性对照表 |
(2) 基于多元关系的数据集
JF17K和Wikipeople是目前用于多元关系链接预测的主流数据集.
JF17K: Wen等人[24] 2016年从知识图谱Freebase中提取出JF17K数据集, 用于更好地研究包含非二元关系的知识嵌入. 作者下载了完整RDF格式的FreeBase数据, 对其中被提及次数极少的实体, 以及其中涉及字符串、枚举类型或数字信息的三元组进行过滤, 之后从其余三元组中恢复出多元事实知识的表示. 最后, 作者进行了进一步过滤, 以确保每个实体至少涉及5个实例.
虽然开创性提出多元关系的表示形式并抽取出对应数据集, Wen等人抽取的JF17K数据集也存在大量数据泄漏问题: 测试集中44.5%的主三元组也出现在训练集中. 此外, 该数据集提出时并未设置验证集, 导致部分后续模型在使用该数据集时需要从训练集中随机抽取一部分数据作为验证集.
Wikipeople: Guan等人[86]在2019年从知识图谱Wikidata中抽取出与人类实体类型相关的多元关系数据集Wikipeople. 作者选择了Wikidata中所有被提及30次以上的元素, 将与之相关的全部知识以角色-键值对形式进行存储后, 对多元组知识进行去噪, 将所有包含图像元素与包含
虽然有能力存储多元关系知识, 但Wikipeople数据集所涉及的多元关系知识十分有限, 其在全部知识中的占比不到12%, 若去掉各种数字信息(例如具体日期和其他字符串信息), 剩余的多元关系知识在全部知识中的占比只剩不到3%. 因此, 以该数据集作为基准时, 研究人员难以对知识表示学习模型在多元关系上的链接预测进行充分评测.
(3) 基于超关系的数据集
超关系作为多元关系的优化表示形式, 对基于多元关系的数据集具有兼容性. 然而, 为弥补Wikipeople和JF17K数据集的缺陷, Galkin等人[88] 2021年从Wikidata中抽取出专门用于超关系链接预测的数据集WD50K.
WD50K: 作者选取了一组对应于FB15k-237数据集实体的种子节点, 对于每个种子节点, 提取出其主对象和限定词键值对所对应
WD50K数据集中14%的语句至少存在一个限定词键值对(即存在14%的超关系事实知识). 为进一步探究算法模型在超关系知识图谱中进行链接预测的性能, 作者还从WD50K中抽取出WD50K(33), WD50K(66), WD50K(100)这3个子集(括号内的数字代表超关系知识在全部知识中的占比百分数).
我们将用于多元化关系链接预测的3个数据集的重要属性列在表5中(表中实体(N)与关系(N)代表仅出现于多元知识中的实体与关系数量), 以便于进行对比分析.
| 表 5 多元化关系数据集属性对照表 |
在预测过程中, 链接预测模型需要将数据集中存在的全部实体或关系依次填补进需要预测的知识空缺位置中, 并对每一个实体或关系(取决于该空缺位置是实体还是关系)进行打分, 再根据打分结果进行排序. 基于此, 链接预测的实验中常用平均秩(mean rank, MR)、平均倒数秩(mean reciprocal rank, MRR)和命中比率Hits@K (H@K)这3种度量指标对模型进行预测效果评测[23].
(1) MR度量
MR即对每个链接预测任务所对应真实答案在预测结果中的排名取平均值. 在早期的链接预测任务中, 研究人员多使用MR作为量度, 其定义如下:
| MR=1|Q|∑q∈Qq | (32) |
其中, 存在
(2) MRR度量
MRR即对每个链接预测任务所对应真实答案在预测结果中排名的倒数取平均值, 其具体定义如下:
| MRR=1|Q|∑q∈Q1q | (33) |
MRR存在
(3) H@K度量
H@K即预测中正确答案的排名结果等于或小于阈值K的比率:
| H@K=|{q∈Q:q⩽K}||Q| | (34) |
H@K的值越高, 模型的预测效果越好. 在链接预测实验中, K的常用取值有
由于侧重不同, MRR和H@K不能代替彼此. MRR取平均值, 侧重于评测模型的整体预测效果; H@K侧重于根据上层具体应用, 基于对预测准确率粒度的不同要求, 进行有针对性的测试评测. 鉴于MR度量对离群值高度敏感, 稳定性明显不足于MRR, 本节选取MRR, H@1和H@10这3个评测指标进行实验效果对比.
虽然被使用广泛, 但是上述3个评测指标的缺点也较为明显: MR、MRR和H@K均基于正确答案在全部预测结果中的排名进行评测, 当存在排名较高但得分极低的答案时, 当前评测指标将无法准确评估模型的优劣, 因此用于链接预测的知识图谱表示学习模型还应进一步完善更加全面高效的评测指标.
5.3 算法模型实验对比分析表6–表8分别展示了面向二元关系和多元化关系链接预测的知识表示学习模型在各自常用数据集上的实验结果, 实验结果参考上述文献[23]等(不同模型的实验结果参考文献引用在模型一栏中, 实验结果参考文献与提出模型的参考文献不一定为同一文献), 加粗数据表示当前指标中最好的结果.
| 表 6 部分二元关系链接预测结果 |
| 表 7 不同数据集之间的模型实验结果对比 |
(1) 平移距离模型分析
如表6所示, 二元关系中的平移距离模型整体效果不够稳定. 当涉及较为严苛的度量(如H@1和MRR)时, 大部分平移距离模型都表现不佳. 目前, 该系列最有效的模型是RotatE, 其在各数据集的指标中都表现出众, 这一定程度上得益于建模时加入的旋转. 该操作大幅度提升了模型的表达能力, 使得该模型可以针对1-N关系、对称关系、反对称关系和反向关系均有较好的建模能力, 突破了传统平移距离模型难以建模复杂关系的缺陷. 虽然实验效果不够稳定, 但由于其直观的映射建模方式, 即将三元组表示为头实体向量到尾实体向量变换过程的映射方式, 使得此类模型在链接预测的实际应用中具有较好的可解释性, 同时对传递关系天然具有表达能力. 此外, 该算法复杂度较小, 在大规模知识图谱的应用上更为现实.
虽然明确的语义建模可以带来更强的可解释性, 但从表7和表8所示的多元化关系知识表示学习模型中可以看出, 受其明确语义建模的影响, 平移距离模型在进行多元化的推广时更易存在预测限制, 例如m-TransH和RAE均只能进行实体预测而不能预测关系. 平移距离模型在多元化关系的推广中存在瓶颈, 这也是平移距离模型进一步的研究重点.
| 表 8 同一数据集不同多元化关系知识占比的部分模型实验结果对比[88] |
(2) 张量分解模型分析
在二元关系中, 张量分解模型的实验准确率普遍较高且模型较稳定, 在不同的数据集中的实验性能较为统一. 具体来说, ComplEx在简单数据集上的实验结果较为突出; TuckER模型在复杂数据集上的实验效果最好, 但与之对应的是时间复杂度的提高. TuckER分解所需的时间复杂度达到了
张量分解模型同样受其语义建模和大量约束的限制, 其优势在于可解释性相比基于深度学习的神经网络模型更强, 但在多元化关系推广的过程中也面临诸多困难. 除时间复杂度的问题外, GETD只能预测确定元数的知识, 且超过四元关系的知识将不再适用. GETD的作者在论文中将Wikipeople和JF17K两个数据集分别进行了三元知识和四元知识的抽取, 再进行实验(表7中的GETD-3和GETD-4分别代表GETD模型预测三元关系知识图谱和四元关系知识图谱), 因此模型的训练很有方向性, 预测准确率也更高. 但受限于固定元数的知识, GETD难以与其他模型横向对比. S2S虽然解决了GETD只能预测确定元数知识的问题, 但从表7中可以明显看出该模型在预测低元数关系知识时表现较差, 因此在实际应用中难以发挥其最大作用.
(3) 传统神经网络模型分析
神经网络模型的实验效果极大程度上取决于对三元组信息的特征提取方式. 在二元关系预测中, ConvR令实体向量与关系向量充分交互, 获得的综合实验效果最为出众; ConvKB只对三元组信息进行了简单的一维卷积, 其H@1和MRR指标下的实验结果相对较差. 此外, 多样化的神经网络架构也发挥着重要作用. 相比较而言, 卷积神经网络是该领域目前发展最为成熟的网络模型, 基于循环神经网络和胶囊网络的模型表现均不够稳定, 还有较大发展空间.
由于不受限于明确的语义建模, 神经网络模型在多元化关系的推广上限制明显减少, 从表7中可以明显看出神经网络模型在多元化关系预测中的大量使用. 同时, 获益于良好的推广性, 基于神经网络模型的超关系的知识表示学习模型首次出现. 但缺少固定的语义限制也使神经网络模型更趋近于纯数据驱动的黑盒模型, 因此存在可解释性差的问题. 在未来研究中, 依然需要深入探索基于深度学习的神经网络知识表示学习模型的可解释性问题.
(4) 图神经网络模型分析
图神经网络模型是现有算法中最有发展前途的一类模型. 该模型作为建模结构化数据的强大架构, 不仅使得深度学习模型能够应用在图这种非欧几里德结构上, 还为深度学习模型赋予了一定的因果推理能力[72], 在诸多领域的应用中都有着巨大优势, 这使得该类模型成为知识表示学习领域的一个重要发展方向.
从表6和表7中可以看出, 用于链接预测的图神经网络模型均取得不菲的成绩: 二元关系模型CompGCN在多个指标上均获得了最好的性能; StarE模型更是将图神经网络模型推广到超关系的链接预测中, 获得了多元化知识表示学习模型中最佳的性能.
尽管目前基于图神经网络的表示学习模型性能较好, 但该模型也有其自身的发展瓶颈: 首先, 堆叠多层GNN网络会令节点之间的特征过于平滑, 导致其性能变差, 因此现有GNN都是浅层结构; 其次, GNN在计算节点特征时依赖大量邻居节点, 并且需要计算图的拉普拉斯算子, 这些依赖都导致了巨大的计算开销, 使GNN难以应用于大规模知识图谱中; 此外, 与传统神经网络类似, GNN同样存在可解释性问题[91]. 这些问题在现有的图神经网络模型中均有所体现, 虽然Wang等人[92]和Xu等人[93]针对上述问题进行了针对性的初步探索, 但如何有效解决这些问题依然是图神经网络模型未来的研究重点.
(5) 多元化关系模型分析
综合来看, S2S是多元关系链接预测中效果最好的模型. 一方面该模型通过引入共享嵌入片段的思想突破了张量分解模型在多元化推广中的限制, 且有效降低了模型复杂度; 另一方面该模型作为张量分解模型, 其表达能力优于平移距离模型, 可解释性优于神经网络模型, 故在多元关系的预测模型中表现突出.
相较于多元关系模型, 超关系模型存在明显优势, NeuInfer、HINGE和StarE模型在数据集中的优越表现也证明了这一点. StarE成功将图神经网络与超关系链接预测相结合, 获得了多元化关系链接预测任务中最好的实验效果.
尽管实验准确率突出, 现有的超关系知识表示学习模型仍存在大量未解决的问题: HINGE和StarE模型过高的时间复杂度和计算开销, 令其难以适用于大规模的知识图谱应用; 此外, 现有的超关系模型只对限定词键值对与主三元组进行了交互, 忽略了限定词之间的交互关系, 同时限定词与主三元组进行交互的过程中没有针对不同的限定词进行区分, 只是简单地对所有限定词键值对与主三元组进行相似的聚合操作. 因此, 超关系知识表示学习模型还有极大的研究和发展空间.
6 未来研究方向综上所述, 面向链接预测的知识图谱表示学习从提出至今, 已经取得了显著的成果. 无论是知识表示形式的发展, 还是其预测方法的演化, 核心都是尽可能从原图谱中挖掘更多关联信息, 并将这些关联信息更有效地融入预测模型中, 以提高模型的表达和预测能力. 基于此, 该领域还应在以下3个方面进行进一步探索研究.
6.1 模型的深入优化(1) 可解释性
知识表示与推理的可解释性一直是知识图谱领域备受关注的方向. 目前被广泛接受的一种可解释性定义由Miller等人提出, 即可解释性是人们能够理解决策原因的程度[94], 通常基于逻辑规则的决策推理被认为是更具有可解释性的. 区别于基于本体和规则的预测具有事前全局可解释性, 目前知识表示学习模型所具有的可解释性属于事后可解释性[95], 其中平移距离模型和张量分解模型具有相对较强的可解释性. 一方面这两类模型针对知识元组特性设计了具有明确语义的建模方式, 映射过程更为直观; 另一方面这两种建模方式更易与逻辑规则约束相结合, 研究者可以通过设计如路径规则或知识层次规则等约束增强模型的可解释性. 基于深度学习的神经网络模型更趋近于纯数据驱动的黑盒模型, 因此在透明度和可解释性方面长期存在瓶颈, 图结构又给图神经网络的可解释性带来了新的挑战[93]. 未来基于神经网络的知识表示学习研究应与基于逻辑规则的符号推理相结合, 进一步提高预测的可解释性和可靠性.
(2) 可扩展性
链接预测的可扩展性要求模型可以扩展到不同应用场景与表示形式的知识图谱中. 具体地, 扩展到大规模知识图谱要求模型降低计算代价, 例如最近的HoLE模型[55]和GETD模型[83]分别利用循环关联运算和张量环简化向量积, 但简化后的模型复杂度依然较高, 无法扩展到极大规模的实体关系计算中; 扩展到多元化关系的知识图谱要求模型可以对于不同元数知识的处理有统一架构, 基于神经网络的模型在可扩展性上具有一定优势, 其他模型例如S2S[84]利用共享嵌入片段对不同元数知识构造了统一架构, 但有效提高该领域模型的可扩展性仍需进一步进行规则归纳并构建数学上等价的统一框架.
6.2 知识表示形式的持续发展面向链接预测的知识图谱表示形式正经历从二元关系、多关系到超关系的发展. 在该发展过程中, 模型对知识的描述更加清晰, 包含的语义信息更加丰富. 在未来研究中, 除了将现有二元关系的预测方法进一步作多元化推广, 还应有效利用更多图谱自身的特殊结构, 持续探索更加完善的知识表示形式.
除了多元化关系的知识表示形式外, 图谱中还存在层次结构(hierarchical structure)[96]与路径信息[43]等特殊结构. 这类结构带来的大量关系路径为模型提供了丰富的关系模式, 从而提高链接预测效果. 此外, 图谱中还存在对于知识实体的描述与属性信息等附加信息. 如何将这些图谱特有的结构与信息融入预测模型也将是未来的研究重点. 目前, 已有算法以附加约束的形式将这些信息融入模型[43, 96-98], 并取得了不错的效果. 能否以其他方式将这些结构与信息融合入模型, 以及是否需要将部分结构体现在知识表示层面, 都是未来值得研究的方向.
6.3 问题作用域的针对性探索目前的面向链接预测的知识表示学习模型对于问题作用域的探讨仍有不足. 实际场景中, 特定领域的知识库所包含的知识存在不同的语义特性, 其应用需求也不相同, 这要求研究人员在选择预测模型时, 应充分考虑不同场景对模型的特殊需求, 同时在预测准确率、时间复杂度与可解释性之间做出权衡.
例如, 存在大量多跳关系的知识库要求用于知识推理的模型内包含复杂的推理模式[43]; 极大规模的知识库要求模型的在线学习与快速学习能力[99,100], 以及基于知识分布式表示的应用[101]; 低资源条件下的知识图谱补全和知识推理要求模型的少样本甚至零样本学习能力[102-104]. 面向此类特殊知识图谱应用的研究现阶段还不够成熟, 仍需进行深入探索, 以推动面向不同问题作用域链接预测的知识表示学习模型进一步发展.
7 总 结知识图谱表示学习是自动学习知识图谱中实体与关系有效特征的过程, 通常采取将实体和关系嵌入到低维向量空间的方式表示其语义信息. 链接预测是知识图谱补全和知识推理的关键环节, 近年来受到研究者的广泛关注. 本文围绕多元化发展的知识表示形式的链接预测任务, 对4类知识图谱表示学习模型的研究现状进行了总结. 从知识表示形式出发, 链接预测任务可以分为二元关系、多元关系和超关系的表示形式, 其知识表示准确性依次递增. 从表示学习建模方式出发, 可以分为平移距离模型、张量分解模型、传统神经网络模型和图神经网络模型. 在介绍链接预测的常用的数据集与评判标准基础上, 采用对比分析的方式展现面向3类知识表示形式下链接预测任务的4类知识表示学习模型预测效果与优缺点. 最后从模型优化、知识表示形式和问题作用域3个方面展望未来发展趋势.
| [1] |
Xiao YH. From knowledge graph to cognitive intelligence. Communications of the CCF, 2021, 17(3): 60–62 (in Chinese).
|
| [2] |
Vrandečić D, Krötzsch M. Wikidata: A free collaborative knowledgebase. Communications of the ACM, 2014, 57(10): 78-85.
[doi:10.1145/2629489] |
| [3] |
Xiong CY, Power R, Callan J. Explicit semantic ranking for academic search via knowledge graph embedding. In: Proc. of the 26th Int’l Conf. on World Wide Web. Perth: Int’l World Wide Web Conf. Steering Committee, 2017. 1271–1279.
|
| [4] |
Xiong CY, Callan J, Liu TY. Word-entity duet representations for document ranking. In: Proc. of the 40th Int’l ACM SIGIR Conf. on Research and Development in Information Retrieval. Tokyo: ACM, 2017. 763–772.
|
| [5] |
Liu ZH, Xiong CY, Sun MS, Liu ZY. Entity-duet neural ranking: Understanding the role of knowledge graph semantics in neural information retrieval. In: Proc. of the 56th Annual Meeting of the Association for Computational Linguistics (Vol. 1: Long Papers). Melbourne: Association for Computational Linguistics, 2018. 2395–2405.
|
| [6] |
Chen XY, Chen FL, Meng FD, Li P, Zhou J. Unsupervised knowledge selection for dialogue generation. In: Proc. of the 2021 Findings of the Association for Computational Linguistics. Association for Computational Linguistics, 2021. 1230–1244.
|
| [7] |
Meng C, Ren PJ, Chen ZM, Ren ZC, Xi TX, de Rijke M. Initiative-aware self-supervised learning for knowledge-grounded conversations. In: Proc. of the 44th Int’l ACM SIGIR Conf. on Research and Development in Information Retrieval. ACM, 2021. 522–532.
|
| [8] |
Zhang C, Wang H, Jiang FJ, Yin HZ. Adapting to context-aware knowledge in natural conversation for multi-turn response selection. In: Proc. of the 2021 Web Conf. Ljubljana: ACM, 2021. 1990–2001.
|
| [9] |
Chen ZR, Wang X, Wang L, Xu DW, Jia YZ. Survey of open-domain knowledge graph question answering. Journal of Frontiers of Computer Science and Technology, 2021, 15(10): 1843-1869(in Chinese with English abstract).
[doi:10.3778/j.issn.1673-9418.2106095] |
| [10] |
Wang ZY, Yu Q, Wang N, Wang YG. Survey of intelligent question answering research based on knowledge graph. Computer Engineering and Applications, 2020, 56(23): 1-11(in Chinese with English abstract).
[doi:10.3778/j.issn.1002-8331.2004-0370] |
| [11] |
Hu BB, Shi C, Zhao WX, Yu PS. Leveraging meta-path based context for top-N recommendation with a neural Co-attention model. In: Proc. of the 24th ACM SIGKDD Int’l Conf. on Knowledge Discovery & Data Mining. London: ACM, 2018. 1531–1540.
|
| [12] |
Zhang FZ, Yuan NJ, Lian DF, Xie X, Ma WY. Collaborative knowledge base embedding for recommender systems. In: Proc. of the 22nd ACM SIGKDD Int’l Conf. on Knowledge Discovery and Data Mining. San Francisco: ACM, 2016. 353–362.
|
| [13] |
Huang HQ, Yu J, Liao X, Xi YJ. Review on knowledge graphs. Computer Systems & Applications, 2019, 28(6): 1-12(in Chinese with English abstract).
[doi:10.15888/j.cnki.csa.006915] |
| [14] |
Bollacker K, Evans C, Paritosh P, Sturge T, Taylor J. FreeBase: A collaboratively created graph database for structuring human knowledge. In: Proc. of the 2008 ACM SIGMOD Int’l Conf. on Management of Data. Vancouver: ACM, 2008. 1247–1250.
|
| [15] |
Lehmann J, Isele R, Jakob M, Jentzsch A, Kontokostas D, Mendes PN, Hellmann S, Morsey M, van Kleef P, Auer S, Bizer C. DBpedia—A large-scale, multilingual knowledge base extracted from Wikipedia. Semantic Web, 2015, 6(2): 167-195.
[doi:10.3233/SW-140134] |
| [16] |
Suchanek FM, Kasneci G, Weikum G. Yago: A core of semantic knowledge. In: Proc. of the 16th Int’l Conf. on World Wide Web. Banff Alberta: ACM, 2007. 697–706.
|
| [17] |
Pujara J, Miao H, Getoor L, Cohen W. Knowledge graph identification. In: Proc. of the 12th Int’l Semantic Web Conf. Sydney: Springer, 2013. 542–557.
|
| [18] |
Dong X, Gabrilovich E, Heitz G, Horn W, Lao N, Murphy K, Strohmann T, Sun SH, Zhang W. Knowledge vault: A Web-scale approach to probabilistic knowledge fusion. In: Proc. of the 20th ACM SIGKDD Int’l Conf. on Knowledge Discovery and Data Mining. New York: ACM, 2014. 601–610.
|
| [19] |
West R, Gabrilovich E, Murphy K, Sun SH, Gupta R, Lin DK. Knowledge base completion via search-based question answering. In: Proc. of the 23rd Int’l Conf. on World Wide Web. Seoul: ACM, 2014. 515–526.
|
| [20] |
Tian L, Zhang JC, Zhang JH, Zhou WT, Zhou X. Knowledge graph survey: Representation, construction, reasoning and knowledge hypergraph theory. Journal of Computer Applications, 2021, 41(8): 2161-2186(in Chinese with English abstract).
[doi:10.11772/j.issn.1001-9081.2021040662] |
| [21] |
Zhang Y, Meng XF. InterTris: Specific domain knowledge graph representation learning by interaction among triple elements. Chinese Journal of Computers, 2021, 44(8): 1535-1548(in Chinese with English abstract).
[doi:10.11897/SP.J.1016.2021.01535] |
| [22] |
Zhang ZH, Qian YR, Xing YN, Zhao X. Survey of knowledge representation learning methods. Application Research of Computers, 2021, 38(4): 961-967(in Chinese with English abstract).
[doi:10.19734/j.issn.1001-3695.2020.04.0094] |
| [23] |
Rossi A, Barbosa D, Firmani D, Matinata A, Merialdo P. Knowledge graph embedding for link prediction: A comparative analysis. ACM Trans. on Knowledge Discovery from Data, 2021, 15(2): 14.
[doi:10.1145/3424672] |
| [24] |
Wen JF, Li JX, Mao YY, Chen SN, Zhang RC. On the representation and embedding of knowledge bases beyond binary relations. In: Proc. of the 25th Int’l Joint Conf. on Artificial Intelligence. New York: AAAI Press, 2016. 1300–1307.
|
| [25] |
Rosso P, Yang DQ, Cudré-Mauroux P. Beyond triplets: Hyper-relational knowledge graph embedding for link prediction. In: Proc. of the 2020 Web Conf. Taipei: ACM, 2020. 1885–1896.
|
| [26] |
Guan SP, Jin XL, Jia YT, Wang YZ, Cheng XQ. Knowledge reasoning over knowledge graph: A survey. Ruan Jian Xue Bao/Journal of Software, 2018, 29(10): 2966–2994 (in Chinese with English abstract). http://www.jos.org.cn/1000-9825/5551.htm
|
| [27] |
Shu ST, Li S, Hao XH, Zhang LP. Knowledge graph embedding technology: A review. Journal of Frontiers of Computer Science and Technology, 2021, 15(11): 2048-2062(in Chinese with English abstract).
[doi:10.3778/j.issn.1673-9418.2103086] |
| [28] |
Xu YW, Zhang HJ, Cheng K, Liao XL, Zhang ZX, Li L. Comprehensive survey on knowledge graph embedding. Computer Engineering and Applications, 2022, 58(9): 30-50(in Chinese with English abstract).
[doi:10.3778/j.issn.1002-8331.2111-0248] |
| [29] |
Hartig O, Thompson B. Foundations of an alternative approach to reification in RDF. arXiv:1406.3399, 2014.
|
| [30] |
Ravikumar G, Khaparde SA. A common information model oriented graph database framework for power systems. IEEE Trans. on Power Systems, 2017, 32(4): 2560-2569.
[doi:10.1109/tpwrs.2016.2631242] |
| [31] |
Tanon TP, Weikum G, Suchanek F. YAGO 4: A reason-able knowledge base. In: Proc. of the 17th Int’l Conf. on the Semantic Web. Heraklion: Springer, 2020. 583–596.
|
| [32] |
Fatemi B, Taslakian P, Vazquez D, Poole D. Knowledge hypergraphs: Prediction beyond binary relations. In: Proc. of the 29th Int’l Joint Conf. on Artificial Intelligence. Yokohama: Unknown, 2021. 303.
|
| [33] |
Tu K, Cui P, Wang X, Wang F, Zhu WW. Structural deep embedding for hyper-networks. In: Proc. of the 32nd AAAI Conf. on Artificial Intelligence. New Orleans: AAAI Press, 2018. 426–433.
|
| [34] |
Zhang RC, Li JP, Mei JJ, Mao YY. Scalable instance reconstruction in knowledge bases via relatedness affiliated embedding. In: Proc. of the 2018 World Wide Web Conf. Lyon: Int’l World Wide Web Conf. Steering Committee, 2018. 1185–1194.
|
| [35] |
Mikolov T, Chen K, Corrado G, Dean J. Efficient estimation of word representations in vector space. In: Proc. of the 1st Int’l Conf. on Learning Representations. Scottsdale, 2013.
|
| [36] |
Bordes A, Usunier N, Garcia-Durán A, Weston J, Yakhnenko O. Translating embeddings for modeling multi-relational data. In: Proc. of the 26th Int’l Conf. on Neural Information Processing Systems (NIPS). Lake Tahoe: Curran Associates Inc., 2013. 2787–2795.
|
| [37] |
Wang Z, Zhang JW, Feng JL, Chen Z. Knowledge graph embedding by translating on hyperplanes. In: Proc. of the 28th AAAI Conf. on Artificial Intelligence. Québec City: AAAI Press, 2014. 1112–1119.
|
| [38] |
Lin YK, Liu ZY, Sun MS, Liu Y, Zhu X. Learning entity and relation embeddings for knowledge graph completion. In: Proc. of the 29th AAAI Conf. on Artificial Intelligence. Austin: AAAI Press, 2015. 2181–2187.
|
| [39] |
Ji GL, He SZ, Xu LH, Liu K, Zhao J. Knowledge graph embedding via dynamic mapping matrix. In: Proc. of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th Int’l Joint Conf. on Natural Language Processing (Vol. 1: Long Papers). Beijing: Association for Computational Linguistics, 2015. 687–696.
|
| [40] |
Ebisu T, Ichise R. TorusE: Knowledge graph embedding on a lie group. In: Proc. of the 32nd AAAI Conf. on Artificial Intelligence. New Orleans: AAAI Press, 2018. 1819–1826.
|
| [41] |
Sun ZQ, Deng ZH, Nie JY, Tang J. RotatE: Knowledge graph embedding by relational rotation in complex space. In: Proc. of the 7th Int’l Conf. on Learning Representations. New Orleans: OpenReview.net, 2019. 1–18.
|
| [42] |
Ji GL, Liu K, He SZ, Zhao J. Knowledge graph completion with adaptive sparse transfer matrix. In: Proc. of the 30th AAAI Conf. on Artificial Intelligence. Phoenix: AAAI Press, 2016. 985–991.
|
| [43] |
Lin YK, Liu ZY, Luan HB, Sun MS, Rao SW, Liu S. Modeling relation paths for representation learning of knowledge bases. In: Proc. of the 2015 Conf. on Empirical Methods in Natural Language Processing. Lisbon: Association for Computational Linguistics, 2015. 705–714.
|
| [44] |
Lv X, Hou L, Li JZ, Liu ZY. Differentiating concepts and instances for knowledge graph embedding. In: Proc. of the 2018 Conf. on Empirical Methods in Natural Language Processing (EMNLP). Brussels: Association for Computational Linguistics, 2018. 1971–1979.
|
| [45] |
Feng J, Huang ML, Wang MD, Zhou MT, Hao Y, Zhu XY. Knowledge graph embedding by flexible translation. In: Proc. of the 15th Int’l Conf. on the Principles of Knowledge Representation and Reasoning. Cape Town: AAAI Press, 2016. 557–560.
|
| [46] |
Fan M, Zhou Q, Chang E, Zheng TF. Transition-based knowledge graph embedding with relational mapping properties. In: Proc. of the 28th Pacific Asia Conf. on Language, Information and Computing. Phuket: Department of Linguistics, Chulalongkorn University, 2014. 328–337.
|
| [47] |
Xiao H, Huang ML, Hao Y, Zhu XY. TransA: An adaptive approach for knowledge graph embedding. arXiv:1509.05490, 2015.
|
| [48] |
Nickel M, Tresp V, Kriegel HP. Factorizing YAGO: Scalable machine learning for linked data. In: Proc. of the 21st Int’l Conf. on World Wide Web. Lyon: ACM, 2012. 271–280.
|
| [49] |
Yang BS, Yih WT, He XD, Gao JF, Deng L. Embedding entities and relations for learning and inference in knowledge bases. In: Proc. of the 3rd Int’l Conf. on Learning Representations. San Diego, 2015.
|
| [50] |
Trouillon T, Welbl J, Riedel S, Gaussier É, Bouchard G. Complex embeddings for simple link prediction. In: Proc. of the 33rd Int’l Conf. on Machine Learning. New York: JMLR.org, 2016. 2071–2080.
|
| [51] |
Liu HX, Wu YX, Yang YM. Analogical inference for multi-relational embeddings. In: Proc. of the 34th Int’l Conf. on Machine Learning. Sydney: JMLR.org, 2017. 2168–2178.
|
| [52] |
Kazemi SM, Poole D. SimplE embedding for link prediction in knowledge graphs. In: Proc. of the 32nd Int’l Conf. on Neural Information Processing Systems. Montreal: Curran Associates Inc., 2018. 4289–4300.
|
| [53] |
Toutanova K, Chen DQ. Observed versus latent features for knowledge base and text inference. In: Proc. of the 3rd Workshop on Continuous Vector Space Models and Their Compositionality. Beijing: Association for Computational Linguistics, 2015. 57–66.
|
| [54] |
Kadlec R, Bajgar O, Kleindienst J. Knowledge base completion: Baselines strike back. In: Proc. of the 2nd Workshop on Representation Learning for NLP. Vancouver: Association for Computational Linguistics, 2017. 69–74.
|
| [55] |
Nickel M, Rosasco L, Poggio T. Holographic embeddings of knowledge graphs. In: Proc. of the 30th AAAI Conf. on Artificial Intelligence. Phoenix: AAAI Press, 2016. 1955–1961.
|
| [56] |
Hayashi K, Shimbo M. On the equivalence of holographic and complex embeddings for link prediction. In: Proc. of the 55th Annual Meeting of the Association for Computational Linguistics (Vol. 2: Short Papers). Vancouver: Association for Computational Linguistics, 2017. 554–559.
|
| [57] |
Balažević I, Allen C, Hospedales TM. TuckER: Tensor factorization for knowledge graph completion. In: Proc. of the 2019 Conf. on Empirical Methods in Natural Language Processing and the 9th Int’l Joint Conf. on Natural Language Processing. Hong Kong: Association for Computational Linguistics, 2019. 5185–5194.
|
| [58] |
Hitchcock FL. The expression of a tensor or a polyadic as a sum of products. Journal of Mathematics and Physics, 1927, 6(1–4): 164–189.
|
| [59] |
Socher R, Chen DQ, Manning CD, Ng AY. Reasoning with neural tensor networks for knowledge base completion. In: Proc. of the 27th Int’l Conf. on Neural Information Processing Systems. Lake Tahoe: Curran Associates Inc., 2013. 926–934.
|
| [60] |
Krizhevsky A, Sutskever I, Hinton GE. ImageNet classification with deep convolutional neural networks. In: Proc. of the 25th Int’l Conf. on Neural Information Processing Systems. Lake Tahoe: Curran Associates Inc., 2012. 1097–1105.
|
| [61] |
Elman JL. Finding structure in time. Cognitive Science, 1990, 14(2): 179-211.
[doi:10.1207/s15516709cog1402_1] |
| [62] |
Mnih V, Heess N, Graves A, Kavukcuoglu K. Recurrent models of visual attention. In: Proc. of the 27th Int’l Conf. on Neural Information Processing Systems. Montreal: MIT Press, 2014. 2204–2212.
|
| [63] |
Sabour S, Frosst N, Hinton GE. Dynamic routing between capsules. In: Proc. of the 31st Int’l Conf. on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017. 3859–3869.
|
| [64] |
Dettmers T, Minervini P, Stenetorp P, Riedel S. Convolutional 2D knowledge graph embeddings. In: Proc. of the 32nd AAAI Conf. on Artificial Intelligence. Louisiana: AAAI Press, 2018. 1811–1818.
|
| [65] |
Nguyen DQ, Nguyen TD, Nguyen DQ, Phung D. A novel embedding model for knowledge base completion based on convolutional neural network. In: Proc. of the 2018 Conf. of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies (Vol. 2: Short Papers). New Orleans: Association for Computational Linguistics, 2018. 327–333.
|
| [66] |
Jiang XT, Wang Q, Wang B. Adaptive convolution for multi-relational learning. In: Proc. of the 2019 Conf. of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies (Vol. 1: Long and Short Papers). Minneapolis: Association for Computational Linguistics, 2019. 978–987.
|
| [67] |
Vashishth S, Sanyal S, Nitin V, Agrawal N, Talukdar P. InteractE: Improving convolution-based knowledge graph embeddings by increasing feature interactions. In: Proc. of the 34th AAAI Conf. on Artificial Intelligence. New York: AAAI Press, 2020. 3009–3016.
|
| [68] |
Che FH, Zhang DW, Tao JH, Niu MY, Zhao BC. ParamE: Regarding neural network parameters as relation embeddings for knowledge graph completion. In: Proc. of the 34th AAAI Conf. on Artificial Intelligence. New York: AAAI Press, 2020. 2774–2781.
|
| [69] |
Nguyen DQ, Vu T, Nguyen TD, Nguyen DQ, Phung D. A capsule network-based embedding model for knowledge graph completion and search personalization. In: Proc. of the 2019 Conf. of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies (Vol. 1: Long and Short Papers). Minneapolis: Association for Computational Linguistics, 2019. 2180–2189.
|
| [70] |
Guo LB, Sun ZQ, Hu W. Learning to exploit long-term relational dependencies in knowledge graphs. In: Proc. of the 36th Int’l Conf. on Machine Learning. Long Beach: PMLR, 2019. 2505–2514.
|
| [71] |
Scarselli F, Gori M, Tsoi AC, Hagenbuchner M, Monfardini G. The graph neural network model. IEEE Trans. on Neural Networks, 2009, 20(1): 61-80.
[doi:10.1109/TNN.2008.2005605] |
| [72] |
Zhou J, Cui GQ, Hu SD, Zhang ZY, Yang C, Liu ZY, Wang LF, Li CC, Sun MS. Graph neural networks: A review of methods and applications. AI Open, 2020, 1: 57-81.
[doi:10.1016/j.aiopen.2021.01.001] |
| [73] |
Kipf TN, Welling M. Semi-supervised classification with graph convolutional networks. In: Proc. of the 5th Int’l Conf. on Learning Representations. Toulon: OpenReview.net, 2017. 24–26.
|
| [74] |
Velickovic P, Cucurull G, Casanova A, Romero A, Liò P, Bengio Y. Graph attention networks. In: Proc. of the 6th Int’l Conf. on Learning Representations. Vancouver: OpenReview.net, 2018. 1–12.
|
| [75] |
Kipf TN, Welling M. Variational graph auto-encoders. arXiv:1611.07308, 2016.
|
| [76] |
Wu ZH, Pan SR, Chen FW, Long GD, Zhang CQ, Yu PS. A comprehensive survey on graph neural networks. IEEE Trans. on Neural Networks and Learning Systems, 2021, 32(1): 4-24.
[doi:10.1109/TNNLS.2020.2978386] |
| [77] |
Xu BB, Cen KT, Huang JJ, Shen HW, Cheng XQ. A survey on graph convolutional neural network. Chinese Journal of Computer, 2020, 43(5): 755-780(in Chinese with English abstract).
[doi:10.11897/SP.J.1016.2020.00755] |
| [78] |
Schlichtkrull M, Kipf TN, Bloem P, van den Berg R, Titov I, Welling M. Modeling relational data with graph convolutional networks. In: Proc. of the 15th Int’l Conf. on the Semantic Web. Crete: Springer, 2018. 593–607.
|
| [79] |
Vashishth S, Sanyal S, Nitin V, Talukdar PP. Composition-based multi-relational graph convolutional networks. In: Proc. of the 8th Int’l Conf. on Learning Representations. Addis Ababa: OpenReview.net, 2020. 1–15.
|
| [80] |
Shang C, Tang Y, Huang J, Bi JB, He XD, Zhou BW. End-to-end structure-aware convolutional networks for knowledge base completion. In: Proc. of the 33rd AAAI Conf. on Artificial Intelligence. Honolulu: AAAI Press, 2019. 3060–3067.
|
| [81] |
Nathani D, Chauhan J, Sharma C, Kaul M. Learning attention-based embeddings for relation prediction in knowledge graphs. In: Proc. of the 57th Annual Meeting of the Association for Computational Linguistics. Florence: Association for Computational Linguistics, 2019. 4710–4723.
|
| [82] |
Harsha LVH, Jia G, Kok S. Probabilistic logic graph attention networks for reasoning. In: Proc. of the 2020 Web Conf. Taipei: ACM, 2020. 669–673.
|
| [83] |
Liu Y, Yao QM, Li Y. Generalizing tensor decomposition for N-ary relational knowledge bases. In: Proc. of the 2020 Web Conf. Taipei: ACM, 2020. 1104–1114.
|
| [84] |
Di SM, Yao QM, Chen L. Searching to sparsify tensor decomposition for N-ary relational data. In: Proc. of the 2021 Web Conf. Ljubljana: ACM, 2021. 4043–4054.
|
| [85] |
Zhao QB, Zhou GX, Xie SL, Zhang LQ, Cichocki A. Tensor ring decomposition. arXiv:1606.05535, 2016.
|
| [86] |
Guan SP, Jin XL, Wang YZ, Cheng XQ. Link prediction on N-ary relational data. In: Proc. of the 2019 World Wide Web Conf. San Francisco: ACM, 2019. 583–593.
|
| [87] |
Guan SP, Jin XL, Guo JF, Wang YZ, Cheng XQ. NeuInfer: Knowledge inference on N-ary facts. In: Proc. of the 58th Annual Meeting of the Association for Computational Linguistics. Association for Computational Linguistics, 2020. 6141–6151.
|
| [88] |
Galkin M, Trivedi P, Maheshwari G, Usbeck R, Lehmann J. Message passing for hyper-relational knowledge graphs. In: Proc. of the 2020 Conf. on Empirical Methods in Natural Language Processing (EMNLP). Association for Computational Linguistics, 2020. 7346–7359.
|
| [89] |
Mahdisoltani F, Biega J, Suchanek FM. YAGO3: A knowledge base from multilingual Wikipedias. In: Proc. of the 7th Biennial Conf. on Innovative Data Systems Research. Asilomar: www.cidrdb.org, 2015. 1–12.
|
| [90] |
Wang YJ, Ruffinelli D, Gemulla R, Broscheit S, Meilicke C. On evaluating embedding models for knowledge base completion. In: Proc. of the 4th Workshop on Representation Learning for NLP (RepL4NLP-2019). Florence: Association for Computational Linguistics, 2019. 104–112.
|
| [91] |
Ying R, Bourgeois D, You JX, Zitnik M, Leskovec J. GNNExplainer: Generating explanations for graph neural networks. arXiv:1903.03894, 2019.
|
| [92] |
Wang ZH, Ren ZC, He CY, Zhang P, Hu Y. Robust embedding with multi-level structures for link prediction. In: Proc. of the 28th Int’l Joint Conf. on Artificial Intelligence. Macao: IJCAI.org, 2019. 5240–5246.
|
| [93] |
Xu K, Hu WH, Leskovec J, Jegelka S. How powerful are graph neural networks? In: Proc. of the 7th Int’l Conf. on Learning Representations. New Orleans: OpenReview.net, 2019.
|
| [94] |
Miller T. Explanation in artificial intelligence: Insights from the social sciences. Artificial Intelligence, 2019, 267: 1-38.
[doi:10.1016/j.artint.2018.07.007] |
| [95] |
Hou ZN, Jin XL, Chen JY, Guan SP, Wang YZ, Cheng XQ. A survey of interpretable reasoning on knowledge graphs. Ruan Jian Xue Bao/Journal of Software, 2022, 33(12): 4644–4667 (in Chinese with English abstract). http://www.jos.org.cn/1000-9825/6522.htm
|
| [96] |
Li ML, Wang YZ, Zhang DH, Jia YT, Cheng XQ. Link prediction in knowledge graphs: A hierarchy-constrained approach. IEEE Trans. on Big Data, 2022, 8(3): 630-643.
[doi:10.1109/TBDATA.2018.2867583] |
| [97] |
García-Durán A, Bordes A, Usunier N. Composing relationships with translations. In: Proc. of the 2015 Conf. on Empirical Methods in Natural Language Processing. Lisbon: Association for Computational Linguistics, 2015. 286–290.
|
| [98] |
Zhang W, Paudel B, Zhang W, Bernstein A, Chen HJ. Interaction embeddings for prediction and explanation in knowledge graphs. In: Proc. of the 12th ACM Int’l Conf. on Web Search and Data Mining. Melbourne: ACM, 2019. 96–104.
|
| [99] |
Yang XH, Wan R, Zhang HB, Zeng YF, Liu Q. Semantical symbol mapping embedding learning algorithm for knowledge grapg. Journal of Computer Research and Development, 2018, 55(8): 1773-1784(in Chinese with English abstract).
[doi:10.7544/issn1000-1239.2018.20180248] |
| [100] |
Wang HF, Ding J, Hu FK, Wang X. Survey on large scale enterprise-level knowledge graph practices. Computer Engineering, 2020, 46(7): 1-13(in Chinese with English abstract).
[doi:10.19678/j.issn.1000-3428.0057869] |
| [101] |
Xu XR, Feng W, Jiang YS, Xie XH, Sun ZQ, Deng ZH. Dynamically pruned message passing networks for large-scale knowledge graph reasoning. In: Proc. of the 8th Int’l Conf. on Learning Representations. Addis Ababa: OpenReview.net, 2020.
|
| [102] |
Chen MY, Zhang W, Zhang W, Chen Q, Chen HJ. Meta relational learning for few-shot link prediction in knowledge graphs. In: Proc. of the 2019 Conf. on Empirical Methods in Natural Language Processing and the 9th Int’l Joint Conf. on Natural Language Proc. (EMNLP-IJCNLP). Hong Kong: Association for Computational Linguistics, 2019. 4217–4226.
|
| [103] |
Zhang NY, Deng SM, Sun ZL, Chen JY, Zhang W, Chen HJ. Relation adversarial network for low resource knowledge graph completion. In: Proc. of the 2020 Web Conf. Taipei: ACM, 2020. 1–12.
|
| [104] |
Zhang NY, Deng SM, Sun ZL, Wang GY, Chen X, Zhang W, Chen HJ. Long-tail relation extraction via knowledge graph embeddings and graph convolution networks. In: Proc. of the 2019 Conf. of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies (Vol. 1: Long and Short Papers). Minneapolis: Association for Computational Linguistics, 2019. 3016–3025.
|
| [1] |
肖仰华. 从知识图谱到认知智能. 中国计算机学会通讯, 2021, 17(3): 60–62.
|
| [9] |
陈子睿, 王鑫, 王林, 徐大为, 贾勇哲. 开放领域知识图谱问答研究综述. 计算机科学与探索, 2021, 15(10): 1843-1869.
[doi:10.3778/j.issn.1673-9418.2106095] |
| [10] |
王智悦, 于清, 王楠, 王耀国. 基于知识图谱的智能问答研究综述. 计算机工程与应用, 2020, 56(23): 1-11.
[doi:10.3778/j.issn.1002-8331.2004-0370] |
| [13] |
黄恒琪, 于娟, 廖晓, 席运江. 知识图谱研究综述. 计算机系统应用, 2019, 28(6): 1-12.
[doi:10.15888/j.cnki.csa.006915] |
| [20] |
田玲, 张谨川, 张晋豪, 周望涛, 周雪. 知识图谱综述——表示、构建、推理与知识超图理论. 计算机应用, 2021, 41(8): 2161-2186.
[doi:10.11772/j.issn.1001-9081.2021040662] |
| [21] |
张祎, 孟小峰. InterTris: 三元交互的领域知识图谱表示学习. 计算机学报, 2021, 44(8): 1535-1548.
[doi:10.11897/SP.J.1016.2021.01535] |
| [22] |
张正航, 钱育蓉, 行艳妮, 赵鑫. 知识表示学习方法研究综述. 计算机应用研究, 2021, 38(4): 961-967.
[doi:10.19734/j.issn.1001-3695.2020.04.0094] |
| [26] |
官赛萍, 靳小龙, 贾岩涛, 王元卓, 程学旗. 面向知识图谱的知识推理研究进展. 软件学报, 2018, 29(10): 2966–2994. http://www.jos.org.cn/1000-9825/5551.htm
|
| [27] |
舒世泰, 李松, 郝晓红, 张丽平. 知识图谱嵌入技术研究进展. 计算机科学与探索, 2021, 15(11): 2048-2062.
[doi:10.3778/j.issn.1673-9418.2103086] |
| [28] |
徐有为, 张宏军, 程恺, 廖湘琳, 张紫萱, 李雷. 知识图谱嵌入研究综述. 计算机工程与应用, 2022, 58(9): 30-50.
[doi:10.3778/j.issn.1002-8331.2111-0248] |
| [77] |
徐冰冰, 岑科廷, 黄俊杰, 沈华伟, 程学旗. 图卷积神经网络综述. 计算机学报, 2020, 43(5): 755-780.
[doi:10.11897/SP.J.1016.2020.00755] |
| [95] |
侯中妮, 靳小龙, 陈剑赟, 官赛萍, 王元卓, 程学旗. 知识图谱可解释推理研究综述. 软件学报, 2022, 33(12): 4644–4667. http://www.jos.org.cn/1000-9825/6522.htm
|
| [99] |
杨晓慧, 万睿, 张海滨, 曾义夫, 刘峤. 基于符号语义映射的知识图谱表示学习算法. 计算机研究与发展, 2018, 55(8): 1773-1784.
[doi:10.7544/issn1000-1239.2018.20180248] |
| [100] |
王昊奋, 丁军, 胡芳槐, 王鑫. 大规模企业级知识图谱实践综述. 计算机工程, 2020, 46(7): 1-13.
[doi:10.19678/j.issn.1000-3428.0057869] |