前馈神经网络和循环神经网络的鲁棒性验证综述
刘颖
,
杨鹏飞
,
张立军
,
吴志林
,
冯元
软件学报  2023, Vol. 34 2023, Vol. 34 Issue (7): 3134-3166 Issue (7): 3134-3166 |
人工智能的概念诞生于1956年, 彼时人类希望利用机器来模拟人类的思考和决策, 他们发现在处理一些可以利用形式化语言描述的问题时, 电子计算机具有天然的优势. 从此, 人工智能技术开始受到人类的广泛关注, 得到了飞速发展, 其中最具影响力的研究包括Newell等人开发的通用问题求解器[1], 以及Weizenbaum创造出的第1个聊天机器人Eliza[2].
经过60多年的积淀, 计算机的运算能力有了突破性的提升, 以机器学习为主的人工智能技术得到了空前的发展. 深度学习作为机器学习的一个分支, 可以利用神经网络对高维数据的特征进行建模, 学习出相应的超参数来预测新问题, 从而应对现实中的复杂问题. 目前为止, 神经网络的应用已经深入地渗透到医疗诊断[3,4]、语音识别[5,6]、自动驾驶[7,8]、教育娱乐[9,10]、计算机视觉[11, 12]、恶意软件检测[13, 14]等多个领域. 对于自动驾驶领域而言, 自动驾驶系统的每一个环节都可能需要神经网络组件的支持. 例如在感知过程中, 神经网络会将摄像头拍摄的照片作为输入, 进一步识别出照片中包含的交通信号, 如限速或者右转弯; 基于神经网络或者强化学习的控制器再根据这些信号做出相应的决策[7]. 在此过程中, 如果用于感知道路状况的神经网络被黑客恶意攻击, 无法正确识别道路上的交通标志, 便很可能导致意外事件的发生[15]. 即使是训练效果良好的神经网络, 在样本经过扰动或污染后很可能会做出错误预测[16, 17]. 目前已经有许多为神经网络生成对抗性样本的研究[18, 19], 这类对抗性扰动我们人眼很难察觉到, 但是会导致神经网络产生错误的预测. 然而, 想要找到避免此类智能系统被对抗样本攻击或欺骗的方法是相当困难的, 我们很难为神经网络的行为提供一个可靠性保障. 并且由于神经网络的黑盒特性, 人类很难信任它做的决策, 这也是导致难以将神经网络应用于安全攸关系统的主要问题之一.
因此, 研究包含神经网络组件的智能系统的可靠性, 使其行为和决策能被人类理解和认可便尤为重要. 可解释的人工智能(explainable artificial intelligence, XAI) 和人工智能的安全性验证在这类安全需求的驱动下有了快速的发展. 可解释的人工智能专注于为智能算法(神经网络等)的决策附加合理的解释, 例如促使神经网络做出决策的原因或重要特征等[20, 21]. 人工智能的安全性验证则着重研究神经网络在对抗恶意攻击或扰动的情况下是否仍然能够做出正确的决策. 为构建安全可靠的智能系统, 消除神经网络在安全攸关领域中的应用带来的安全隐患, 神经网络的鲁棒性验证(robustness verification) 这一领域应运而生, 世界各地的学者在近年来对其进行了深入的研究.
本文将主要介绍前馈神经网络(feedforward neural network, FNN) 和循环神经网络(recurrent neural network, RNN)这两种常用神经网络的鲁棒性验证方法, 并对这些验证方法之间的内部联系进行梳理和分析. 第2节形式化地定义神经网络的局部鲁棒性质. 第3节从精确算法和近似算法两大类验证算法出发, 详细地介绍FNN的鲁棒性验证方法, 其中精确的验证算法包括基于可满足性模理论、混合整数线性规划这两大类, 近似的验证算法主要包括基于抽象解释、符号传播、凸优化、反例引导的抽象-精化、Lipschitz等验证方法. 我们从算法特性、支持的激活函数与网络结构、可验证的性质、算法精度和验证规模等方面详细地比较各类验证算法, 具体分析可以参考表 1. 第4节简要地介绍RNN的结构, 并于第5节详细地分析各类RNN的验证方法, 主要包括基于抽象解释、将RNN展开为FNN再进行验证、基于自动机提取的验证算法, 并于表 2分析比较了各类验证算法的验证效果. 第6节介绍在大型工业场景下, RNN有关性质的验证方法. 第7节简要介绍FNN局部鲁棒性之外的其他鲁棒性质, 包括全局鲁棒性和概率鲁棒性的定义及验证方法. 第8节阐述未来在神经网络验证领域可行的发展方向, 包括验证神经网络的其他性质, 研究其他网络结构的鲁棒性, 以及验证大型智能系统的安全性等. 第9节对全文内容进行总结.
| 表 1 FNN鲁棒性验证方法比较 |
| 表 2 RNN鲁棒性验证方法比较 |
深度神经网络在结构上由顺序连接的若干层(layer) 组成, 其中起始层称为输入层(input layer), 接收神经网络的输入; 终止层称为输出层(output layer), 输出神经网络的运行结果, 其他中间的层称为隐藏层(hidden layer), 它们是神经网络运行的中间结果. 每一个层由若干神经元(neuron) 构成, 每一个神经元对应一个浮点数变量. 一般的FNN从输出层开始读取输入, 并按相邻两层定义的函数逐层顺序计算, 直到得到输出. 因此, 在数学上神经网络可以建模成一个多元函数
在介绍神经网络的鲁棒性之前, 我们首先梳理神经网络的安全性质. 安全性质(safety property) 是指在给定的条件下, 一个系统完成规定的功能、不失效的能力, 直观上来看即为系统不会产生不安全的行为. 例如“智能汽车永远不会撞到行人以及其他障碍物”就是一个安全性质. 由于这种广义上的安全性质很难被形式化地定义, 本文主要关注将安全性质限制到神经网络中的研究, 即验证神经网络
定义1 (安全性). 给定神经网络
验证此类安全问题的算法在给定神经网络
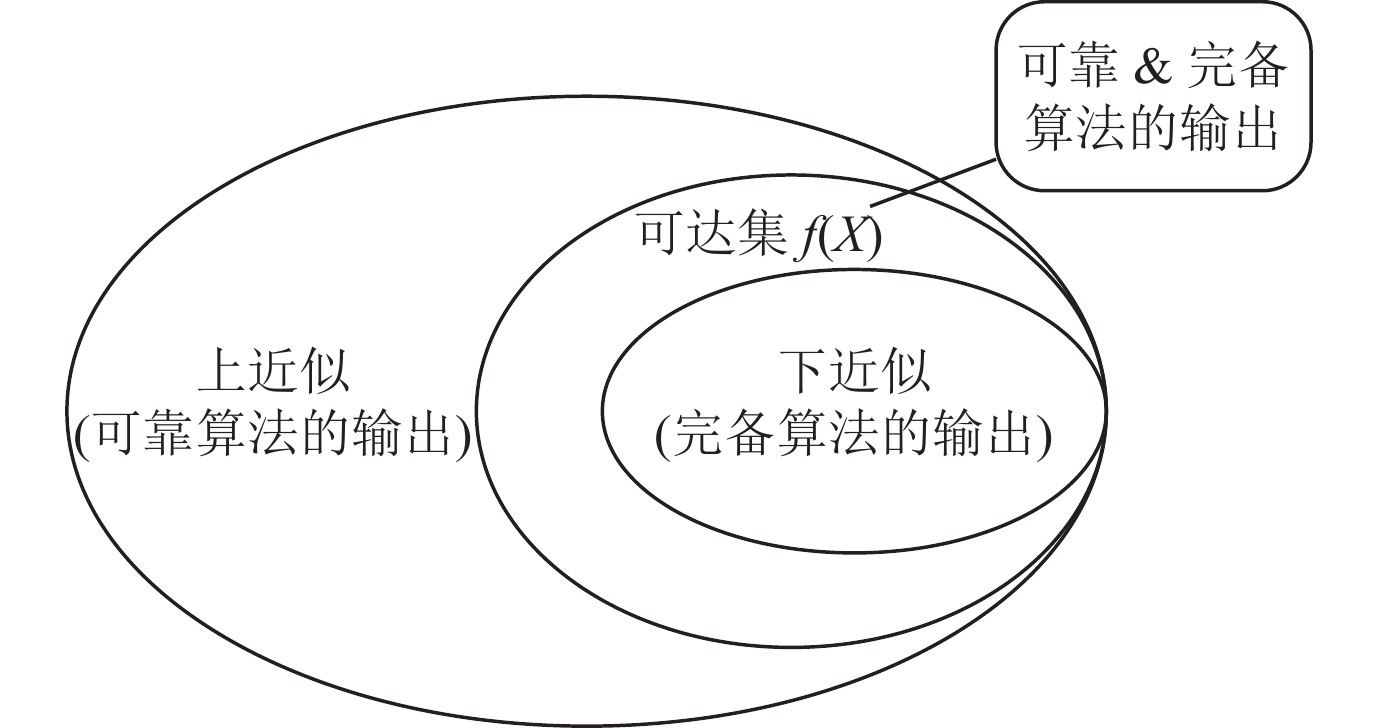
|
图 1 可靠性和完备性示意图 |
在安全性的定义中, 将输入集
定义2 (局部鲁棒性). 给定一个神经网络
| ∀x∈Bp(x0,r),Cf(x)=Cf(x0) |
成立, 我们称神经网络
在本文中, 我们主要关注神经网络的鲁棒性质, 如果没有特别说明, 后文关于神经网络安全性的验证方法均为局部鲁棒性的验证.
在自然语言处理和语音识别等领域, 应用最为广泛的是RNN. 由于RNN比FNN的结构更加复杂, 定义输入序列的扰动空间也更加困难, 因此关于RNN鲁棒性验证的工作目前还比较少, 且多数RNN的验证工作借鉴了FNN的验证思想. 本文将首先回顾FNN鲁棒性验证的相关内容, 分析和比较FNN和RNN验证方法之间的内部联系, 并就RNN验证面临的挑战展开讨论.
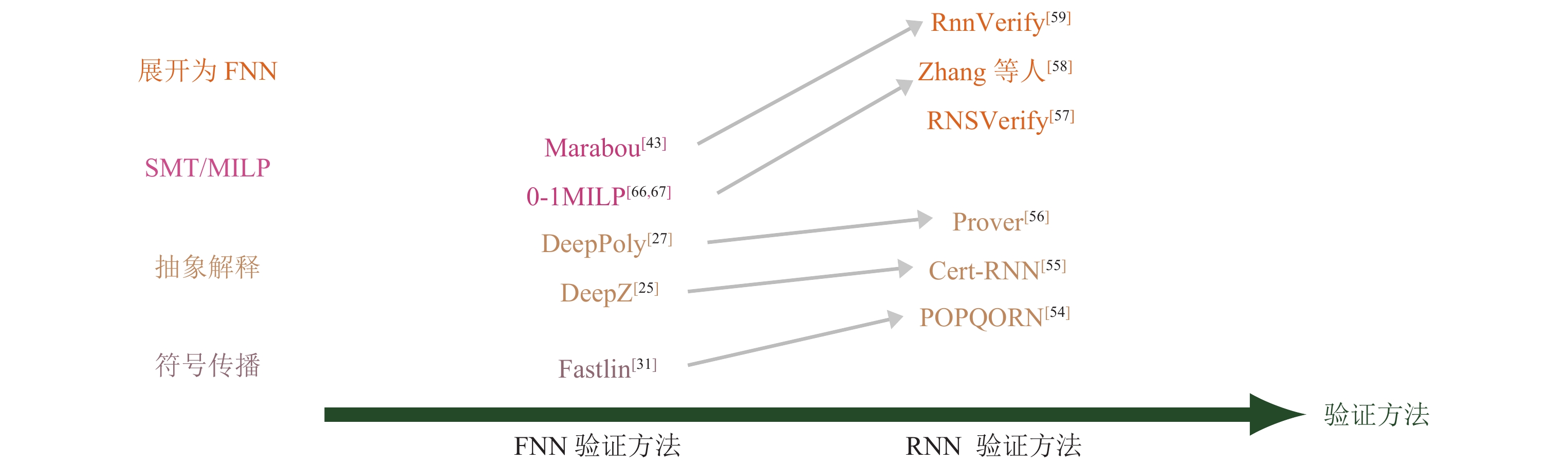
3 FNN验证的研究现状目前针对FNN的验证方法主要分为两大类: 一类是基于可满足性模理论, 混合整数线性规划等优化理论的精确验证方法; 另一类主要是基于凸优化, 抽象解释等近似验证方法. 在后文图 2中, 我们挑选出每一类中比较有代表性的验证方法进行对比[22-26,29-33,38-42,45-47,49-53,64-72]. 其中不同颜色表示不同的验证方法类别, 箭头表示被指向的工具对箭头出发的工具有提升或者是由其借鉴而来, 相同颜色的矩形方框中验证工具的精度相同. 接下来将详细介绍具体的验证方法.
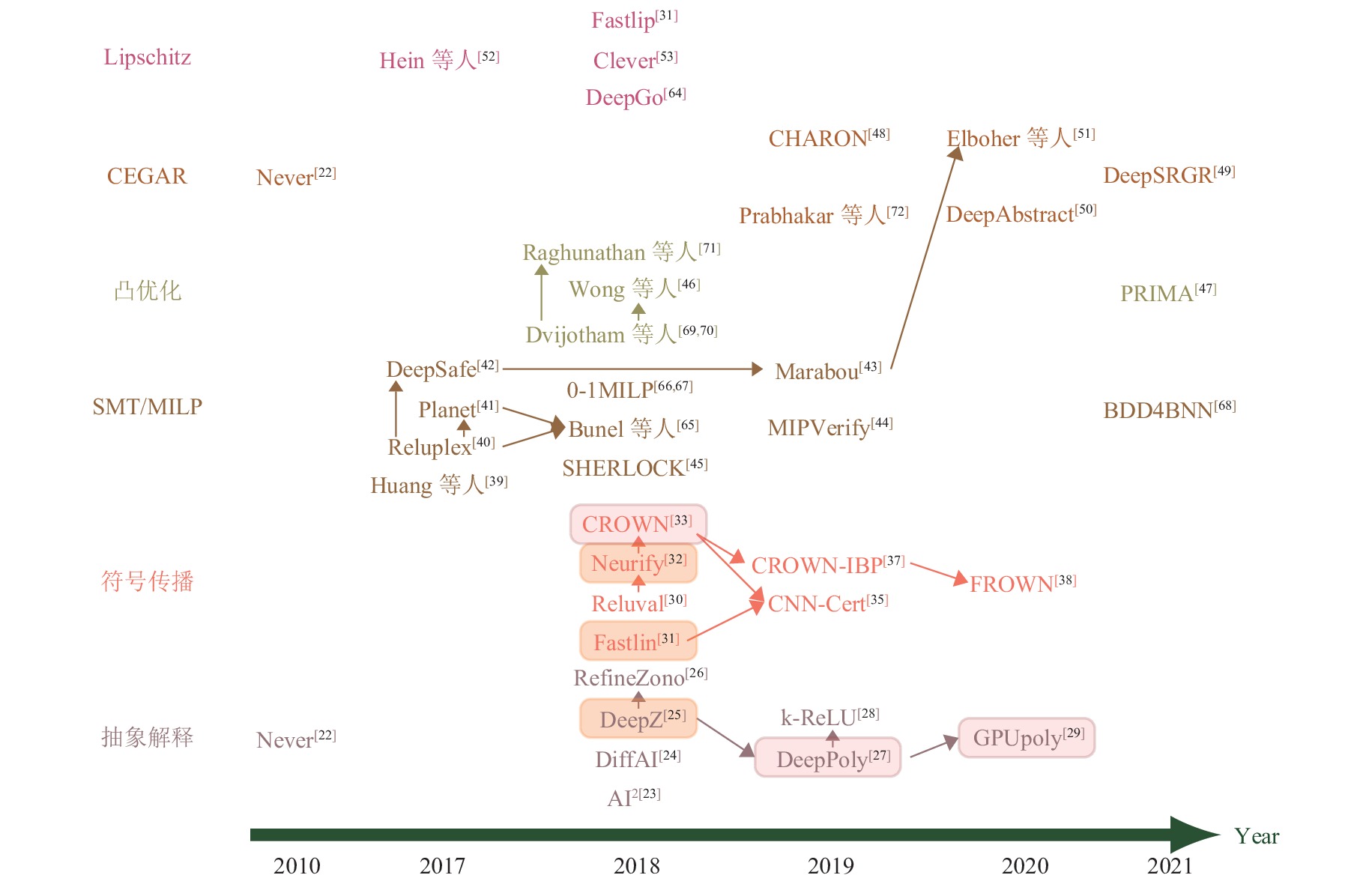
|
图 2 主要的FNN验证方法对比 |
由于神经网络往往规模很大, 并且具有非凸的结构, 所以验证神经网络的复杂度很高. 文献[40, 73]强调即使验证一个很简单的性质也是一个NP完全问题. 目前, FNN鲁棒性的精确验证方法主要包括基于可满足性模理论(satisfiability modulo theory, SMT) 以及混合整数线性规划(mixed integer linear programming, MILP) 这两大类. 基于SMT的验证方法将神经网络鲁棒性验证问题编码为可满足性问题, 然后利用SMT求解器进行验证. 而基于MILP的验证方法是将神经网络的仿射变换以及ReLU激活函数编码为MILP公式(常用的编码方法包括大M法[74]等), 并精确地求解出FNN的可达集, 再判定该可达集是否满足给定的安全性质.
3.1.1 基于SMT的验证方法比较早期的验证方法包括Bastani等人[75]的工作, 他们为神经网络定义了两种不同的鲁棒性, 并利用线性约束来编码整个神经网络的鲁棒性验证问题, 从而将验证问题转化为可满足性问题. 他们通过将输入限制在ReLU函数只取正值或0的区域, 将原来的约束松弛为一个凸约束问题, 从而进行快速求解. Fawzi等人[76]提出了一个理论框架来分析分类器抗扰动的鲁棒性, 并在理论上给出了鲁棒性的一般上界. Scheibler等人[77]考虑了倒立摆的模型检验问题, 倒立摆的控制器是一个具有非线性激活函数的神经网络. 他们使用SMT求解器iSAT3进行求解, 实验表明对于只具有26个节点的神经网络, 解决这个验证问题已经非常具有挑战性. Narodytska等人[78]提出二值化神经网络(binarized neural network, BNN) 可以编码为布尔公式, 并利用SAT求解器对其进行鲁棒性验证, 这也是首次采用精确的布尔编码来验证神经网络的方法, 实验结果显示此验证方法可以处理规模为几百个神经元的神经网络.
以上几种验证神经网络的方法需要对网络结构或性质做出显著的简化, 例如Bastani等人[75]仅考虑所有ReLU函数都固定在激活或非激活状态的小输入区域, 只能验证所需性质的近似值. 基于SMT的验证方法需要求解大规模的约束问题, 因此这类将鲁棒性验证问题编码为SMT公式的验证方法在可拓展性上具有明显的瓶颈.
Huang等人[39]考虑了外部条件变化(例如划痕和不同的天气条件等)对神经网络分类器造成的影响. 相比于前面的工作, 他们基于SMT提出了一种更加灵活的鲁棒性验证方法, 对于一个特定的输入点
Katz等人[40]提出了Reluplex, 将单纯形法(simplex algorithm) 加以拓展得到一个能处理ReLU激活函数的SMT求解器. 具体地, 他们将FNN的仿射变换编码为原子命题的合取形式, 将被ReLU激活的神经元
Katz等人在Reluplex工作中考虑的鲁棒性验证问题为无人机防碰撞系统ACAS Xu[79]中的若干安全性质, 每个ACAS Xu[79]网络包含300个隐藏神经元. Reluplex仅支持ReLU激活函数, 并且这种完备的验证方法具有精确验证效率低下的问题. 因此, 这类基于SMT求解的验证方法无法直接应用到现实中包含数十万个神经元的智能系统[80, 81]. Katz等人[81]介绍了对抗鲁棒性以及其他种类的鲁棒性, 考虑了验证工业界神经网络面临的问题, 并针对自动驾驶系统中FNN控制器的安全性问题, 提出了结合Reluplex进行验证的未来规划.
为了验证含有最大池化(maxpool)节点的神经网络, Ehlers提出了一种基于SMT求解和线性规划的精确验证工具Planet[41]. 他们通过为ReLU激活函数和Maxpool函数添加线性逼近来线性地刻画神经网络的整体行为, 并通过添加冲突字句寻找不可行子集以减少搜索空间, 从而提升搜索效率, 实验表明Planet可以验证具有上千个神经元的神经网络.
Xiang等人[82]通过可达集分析来验证多层感知机(multi-layer perceptron, MLP) 的安全问题, 这是一种结构简单的神经网络. 他们引入了“最大灵敏度”的概念, 并通过求解凸优化问题来计算具有单调激活函数的MLP的最大灵敏度, 将神经网络的可达集估计问题转化为一系列优化问题并求解. 最后他们基于可达集估计的结果开发出一种可靠的自动验证算法.
Gopinath等人提出了一种自动识别输入空间安全区域的完备验证方法DeepSafe[42], 验证神经网络的对抗鲁棒性. 该方法通过数据引导的聚类识别出“候选”安全区域, 然后确认这些区域的安全性, 或者提供证明它们不安全的反例. 他们在MNIST数据集和ACAS Xu网络上评估发现DeepSafe可以准确地确定神经网络的安全输入区域.
Katz等人在Reluplex[40]的基础之上又提出了Marabou[43], 支持具有任意线性激活函数的FNN和卷积神经网络(convolutional neural network, CNN)的验证, 在应用广泛性上相对于前身Reluplex有了新的突破. Marabou是基于SMT的验证框架, 其内置了基于单纯形法的线性规划求解器, 并设置了一个很小的超时阈值, 当求解时间达到该阈值时, 求解器将验证过程划分为更简单的子过程, 在不同节点上并行地运行子查询. 相比于Reluplex在每次迭代中都要将线性规划问题翻译成外部求解器GLPK接受的输入, 并从中提取相应的结果, Marabou大大提升了线性规划问题的求解效率. 在ACAS Xu网络上的实验表明, Marabou相比于Reluplex和Planet等工具在验证效率上具有明显的优势.
Zhang等人提出了BNN的分析框架BDD4BNN[68]. 他们将BNN视为黑盒, 将BNN和输入区域编码为可以表示为布尔函数的二进制决策图(binary decision diagrams, BDD) 并基此设计了BNN的鲁棒性分析框架, 并且支持可解释性分析, 实验表明BDD4BNN框架可以验证上千个神经元的神经网络.
基于SMT的验证方法由于编码过程时间代价高昂, 在约束空间规模庞大的情形下, 通常只能处理神经元数量在几千以内的神经网络, 并且SMT求解器具有难以求解非线性问题的局限性, 基于SMT的鲁棒性验证方法往往只能处理ReLU或者其他具有线性激活函数的神经网络.
3.1.2 基于MILP的验证方法神经网络可以被编码为MILP公式. 在较为早期的研究中已经有了相关的工作, 例如Fischetti等人提出的0-1 MILP框架[66, 67], 用连续变量来表示每一个神经元的输出值, 离散变量表示ReLU激活过程; Lomuscio等人[83]利用大M法将FNN编码为MILP公式, 并且将FNN的可达性问题编码为LP问题进行求解等.
Cheng等人[84]开发了基于MILP的启发式算法, 并采用了一些优化方法提升求解效率. 例如在用MILP求解神经元范围时, 同时考虑前几层的神经元范围, 将全局MILP问题分割为若干个更小的子问题; 为不同隐藏层的神经元设置编码优先级等. 以上优化方法显著地减少了MILP求解器的运行时间, 与普通的MILP编码过程相比, 他们的优化策略在一些特殊的MNIST基准数据集上甚至可以使得运行效率提升两个数量级.
Dutta等人提出了一种有效的可达集估计算法SHERLOCK[45], 在MILP全局优化和基于局部搜索的局部优化之间不断迭代, 通过修剪次优节点, 有效提升了激活神经元的搜索速度. SHERLOCK很好地利用了神经网络的局部连续性和可微特性, 同时又避免了局部搜索可能陷入局部最小值的困境, 在效率上也优于传统的完全基于SMT或者MILP的验证方法. 实验显示SHERLOCK能验证具有6000个神经元的神经网络. 该算法专注于验证以ReLU作为激活函数的FNN, 而对于其他类型的激活函数, 例如Sigmoid和tanh, SHERLOCK不具备求解能力.
需要注意的是, SHERLOCK虽然利用了MILP技术求解神经网络的输出范围, 但是在编码ReLU函数的过程中添加了一个微小的松弛, 因此SHERLOCK得到的是神经网络输出的上近似. 为了便于归类, 我们仍于此处介绍SHERLOCK方法.
Bunel等人[65]利用分支限界等优化方法, 将Reluplex、Planet等基于SMT、MILP的主流验证方法纳入一个统一的验证框架中, 并强调Reluplex、Planet在该框架中只是一个特例. 他们另一个重要贡献在于从现有的神经网络验证文献中收集并拓展得到一个新的基准数据集(benchmark) 并命名为PCAMNIST, 并在此数据集上将分支限界处理后的Reluplex和Planet等算法进行比较, 同时通过在更小的区域上精化ReLU的上下界, 采取分支策略分割输入域等优化方法, 对以上验证算法提出了可能的改进, 大大提高了算法效率.
利用MILP验证神经网络的比较有影响力的工作还包括Tjeng等人提出的MIPVerify[44], 他们将神经网络编码为MILP问题并求解, 设计了一些剪枝方法缩小搜索空间, 大大提高了求解效率, 已经可以验证中等规模的神经网络, 相对于之前的基于SMT的验证方法实现了不小的突破, 甚至可以拓展到带有卷积层和残差层的网络结构中.
虽然基于SMT和MILP的验证方法能够精确地确定神经网络的可达集, 并且近年来在神经网络鲁棒性验证领域中取得了很大的进展, 但是由于此类方法具有编码复杂、时间代价大的缺点, 能验证的网络规模比较小, 拓展到具有上万个神经元的神经网络仍然具有很大的挑战. 同时, 在许多现实情况下, 验证神经网络的性质并不需要得出其确切的可达集, 即如果可达集的上近似满足某安全性质, 则该可达集必然也满足这一性质. 因此从2018年左右开始, 更高效的近似验证方法逐渐兴起.
3.2 近似验证方法FNN的近似验证方法相比于为数不多的可靠且完备的精确验证方法来说, 正处于快速发展的状态, 主要的近似验证方法包括基于抽象解释、符号传播、Lipschitz、凸优化以及反例引导的抽象-精化等验证方法.
3.2.1 基于抽象解释的验证方法基于抽象解释验证神经网络的方法主要是利用抽象域在神经网络中逐层传播, 最后得到神经网络可达集的上近似, 并判断该上近似是否满足给定的安全性质. 最早的神经网络验证方法是由Pulina等人提出的Never[22]验证框架, 这也是最早的利用抽象解释验证神经网络的框架. 他们用区间定义神经网络
为了将抽象解释的验证方法拓展到规模更大, 结构更一般的神经网络中, Gehr等人提出了第1个可靠、可拓展的ReLU神经网络验证框架AI2[23]. 他们利用区间抽象域和Zonotope抽象域[87]为扰动之后的输入添加一个可靠的边界, 并构造了基于Zonotope的抽象转换器来执行神经网络中的各种非线性操作, 包括ReLU激活函数和最大池化层, 最后验证输出的Zonotope是否满足给定的性质. 由于Zonotope本身形状简单, 对真实可行域的松弛在有些验证场景中过于宽松, 并且在传播过程中会逐层放大误差, 其验证精度有所局限.
Mirman等人提出了一种基于混合Zonotope的鲁棒性训练和验证方法DiffAI[24]. 混合Zonotope是指在Box抽象域的基础之上添加一些形如Zonotope的偏移量, 作为一个表达能力等同于Zonotope的新抽象域. 他们在此基础上定义了一个损失函数来训练神经网络, 并通过梯度下降等技术进行优化, 通过这种方法训练得到的网络具有良好的鲁棒性和可拓展性. Mirman等人在后续的工作[88]中引入了两个新概念: ① 用于微调抽象精度和可扩展性的抽象层; ② 用一种灵活的领域专用语言(domain specific language, DSL) 来描述神经网络中抽象损失与具体损失相结合的目标函数, 并提出为大型残差网络ResNet提高鲁棒性的训练方法.
Singh等人提出的DeepZ框架[25]进一步解决了AI2的可拓展性问题, 适用于ReLU, Sigmoid, tanh等多种激活函数和前馈、卷积以及残差网络等多种神经网络结构. 类似于AI2, DeepZ也采用了Zonotope抽象域对神经网络的扰动区域进行松弛, 但DeepZ利用面积最小化原理为ReLU, Sigmoid, tanh等激活函数提供了一种更紧的可靠的抽象方式, 并利用Zonotope在神经网络中的传播求解最后一层神经元的范围, 从而验证网络的鲁棒性.
以上验证方法都是利用Zonotope抽象域在神经网络中逐层传播, 是当前神经网络鲁棒性验证领域比较主流的方法. 但是这种不完备的松弛方法会导致在每一个神经元执行激活操作时引入比较大的误差, 并且在传播过程中也会造成精度损失. 因此该抽象域在松弛精度上存在缺陷, 最后一层神经元的范围可能会被放大成百上千倍.
Singh等人提出了DeepPoly[27], 进一步提升了抽象域的精度. DeepPoly基于线性不等式, 为每个神经元添加两个符号界约束
为了解决Zonotope抽象域带来的精度损失问题, 很多新的验证方法也在此基础上应运而生. Singh等人提出了RefineZono[26], 将Zonotope抽象域和MILP、LP结合起来验证神经网络. 他们用Zonotope抽象域求解得到每一层神经元的范围, 然后利用MILP求解器精化该范围, 从而得到更紧的神经元边界, 再进一步往前传递分析. RefineZono得到了比DeepPoly更高的验证精度, 但是MILP的应用导致运行时间上存在一些劣势.
为了更进一步地提升传递效率, Müller等人将区间分析的高效传播和DeepPoly的高精度这两个优势结合起来, 并利用了GPU的并行性提出了GPUPoly框架[29]来验证神经网络. 在DeepPoly框架中, 得到神经元的数值上下界需要反向传播到输入层, 因而效率低下, GPUPoly利用区间分析来代替这一反向传播过程: 在求解每个神经元的数值界时, 他们为神经元的边界添加一个可靠的区间抽象, 如果当前神经元处于确定的激活或者未激活状态, 即可省略反向传播的过程, 反之则利用DeepPoly反向传播得到神经元的上下界. 得益于高并行的设计, GPUPoly的精度等同于DeepPoly, 但是验证速度比DeepPoly快35倍到170倍.
此外, Singh等人还在DeepPoly的基础上提出一种带参数的精化框架k-ReLU[28], 在求解每一层神经元的符号界时, 同时考虑
上述基于抽象解释的验证方法以较高的效率得到神经网络一个可靠的输出范围, 并且可以拓展到中等规模的神经网络. 由于神经网络真实的可达集真包含于抽象解释得到的输出范围, 当抽象域过于松弛的时候, 很容易产生虚假反例. 即, 若抽象解释得到的范围不满足给定的性质, 便很难证验证真实的输出是否满足该性质, 这也是验证算法可能会得到“Unknown”结果的原因. 因此产生了反例引导的抽象-精化框架来验证神经网络.
3.2.2 基于网络结构抽象/反例引导的抽象-精化的验证方法当验证算法对神经网络的抽象过于松弛时, 输出范围中可能含有许多不属于安全范围内的“反例”. 如果这些“反例”对应的原始输入经过神经网络传递之后得到的真实输出是属于安全范围的, 我们将这些“反例”称为“假反例”; 反之, 若这些“反例”的原始输入对应的输出也在安全范围之外, 则称为“真反例”, 其直观含义如图 3所示. 基于反例引导的抽象-精化方法(counterexample guided abstraction refinement, CEGAR) 通过抽象模型得到的假反例, 将过于松弛的抽象进行精化, 从而迭代地得到一个更精确的验证结果.
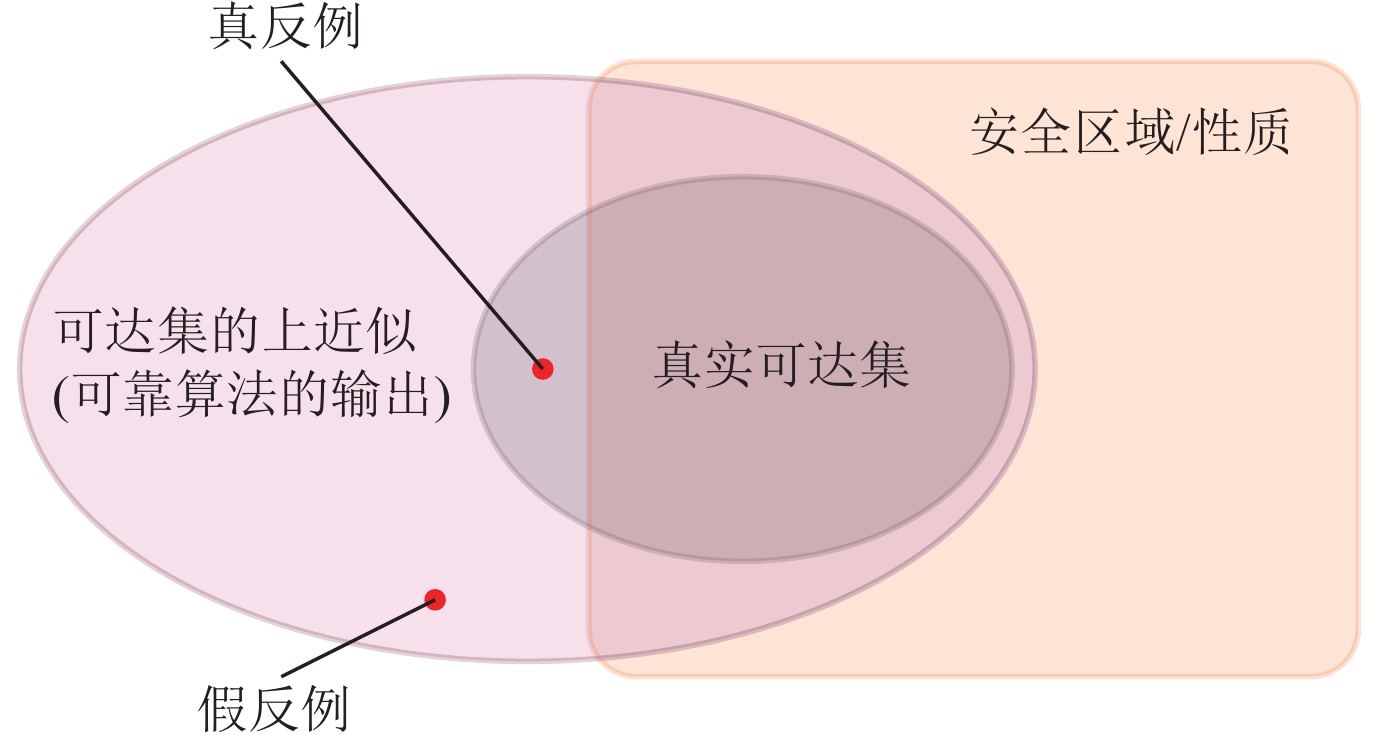
|
图 3 真反例和假反例示意图 |
反例引导的抽象-精化方法通常会与抽象解释等松弛方法结合起来验证神经网络的鲁棒性. 其原理为: 利用抽象解释验证神经网络时, 如果因为对可达集松弛过大而无法验证给定的安全性质, 就会触发精化方法得到更紧的抽象域或者更细粒度的抽象. 例如前面介绍的Never框架[22], 当利用抽象解释在可达集的上近似中发现反例时, 会触发神经网络的自动修复, 这是比较早期的将抽象与精化结合起来验证神经网络的方法.
除了与抽象解释相结合, 精化方法还可以与其他的松弛方式相结合验证网络, 例如对网络结构进行抽象. 对网络结构进行抽象的方法主要通过删除、合并多余的神经元来减小神经网络的规模, 并得到神经网络输出范围的上近似. 然而改变神经网络的结构很可能因为过度放大权重导致输出范围过度松弛, 此时基于反例引导的抽象-精化方法可以得到更紧、更准确的输出范围.
早在2015年, Srinivas等人[89]提出可以通过移除神经元简化神经网络的结构, 同时保持和原始神经网络相似的性能. 他们计算传入某一层神经元的权重之间的相似性度量, 然后通过合并那些最相似的权重来移除“多余”的神经元, 并对移除神经元的数量和准确性之间的关系进行了分析. 类似地, Zhong等人[90]通过聚类对权重进行合并, 从而压缩神经网络的规模. Han等人[91]引入了“深度压缩”方法——一个3阶段的工作流程: 修剪、量化权重和霍夫曼编码, 在不影响神经网络准确性的条件下压缩神经网络的规模, 使得神经网络的存储需求减少数十倍. 以上通过修剪、抽象网络结构来压缩神经网络的方法, 目的是减少神经网络的内存消耗, 并不对神经网络的安全性进行验证.
关于利用抽象网络结构来验证神经网络的安全性的工作, Prabhakar等人[72]考虑了FNN的可达性分析问题. 他们将神经网络的权重矩阵和偏差向量分别抽象为区间, 形成区间神经网络(interval neural network, INN), 示意图如图 4所示. 具体地, 他们将同一隐藏层的两个神经元合并到一起, 与这两个神经元有关的权重和偏差将拓展为区间的形式, 该区间是合并之前神经元权重和偏差的凸包, 从而确保合并后网络的输出为原神经网络可达集的上近似. 他们利用MILP编码最终得到的区间神经网络并求解输出范围. 通过这种方法将神经网络抽象为一个结构更简单、神经元数量更少的区间神经网络, 实现计算复杂度和输出精度之间的权衡. 由于被合并神经元的选取对最终的精度影响很大, 因此如何通过选择合适的神经元提高抽象神经网络的精度, 以及当神经网络过于松弛时如何采取精化措施来修正抽象过程是这项工作的难点.
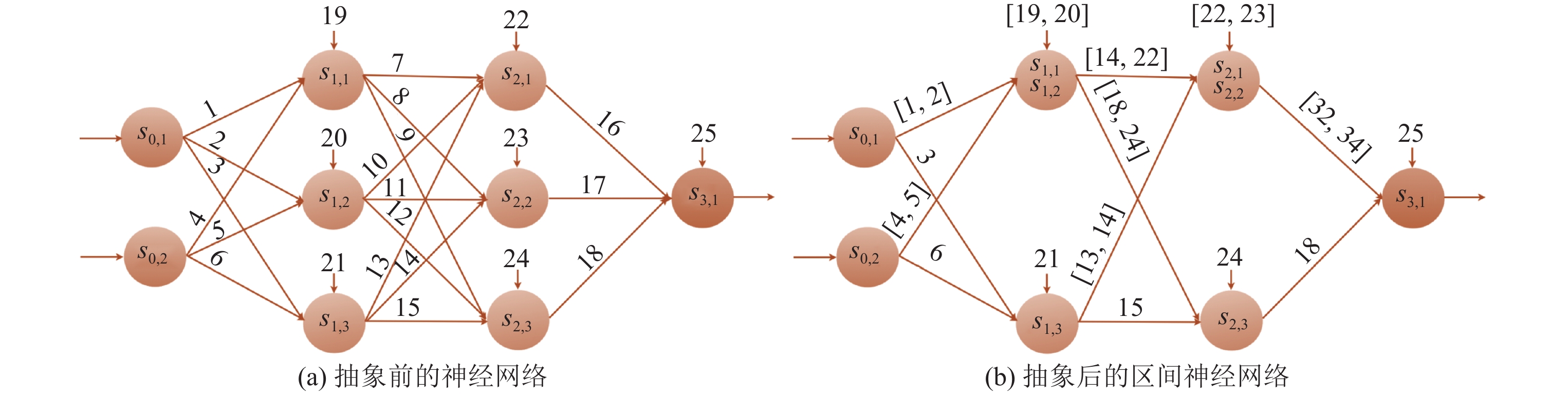
|
图 4 通过将普通FNN的权重矩阵元素抽象为区间表示可以减少神经元数量, 神经元上方的数字表示偏差 |
可靠的Zonotope抽象域可以确定神经网络输出范围的上近似, 但是由于抽象域过于松弛, 会经常导致假反例的产生. 另一方面, 基于优化寻找反例的过程可以高效地寻找到对抗性扰动, 但如果没有搜索到反例, 则很难证明神经网络是鲁棒的. Anderson等人将这两种策略的优势相结合, 提出了鲁棒性验证方法CHARON[48], 在验证的同时寻找反例, 又利用找到的反例对抽象过程进行精化. 这是一种可靠且
Ashok等人提出一个适用于全连接FNN的抽象框架DeepAbstract[50], DeepAbstract基于启发式的K-means聚类方法, 将在输入上表现相似(I/O相似)的神经元进行聚类, 然后在同一层中合并这些具有I/O相似性的神经元, 从而减小神经元的规模, 提高验证效率. 与纯粹的压缩技术相比, 他们的抽象提供了原始神经元和抽象神经元之间的一个映射, 便于将抽象网络的鲁棒性验证结果转移到原始神经网络上, 从而得到原始神经网络的验证结果. 在实验中他们展示了如何利用DeepPoly验证抽象网络, 并迁移到对原始神经网络的验证中.
Elboher等人[51]通过对神经元的性质进行分类, 将每个神经元分为pos/neg和inc/dec这4种类型, 并迭代地将类别相同的神经元进行合并, 减小神经网络规模. 他们利用Marabou来验证抽象之后的网络, 并在抽象过于松弛的情况下采用反例引导的抽象-精化, 对神经网络结构的抽象进行细化. 这类方法将抽象带来的高效率与反例引导的抽象-精化带来的高精度相结合, 很好地实现了神经网络验证精度和效率上的平衡.
在最近的工作中, Yang等人在DeepPoly抽象域的基础上, 提出了伪区域指导的神经网络验证精化技术DeepSRGR [49], 该方法在验证精度需求较高, DeepPoly抽象域难以成功验证的场合, 可以利用通过性质取反构造的伪区域, 精化关键变量在伪区域语义中的上下界, 从而大幅提升DeepPoly抽象域的验证精度. 在该方法的框架下, 每次精化的过程并不会生成具体的反例, 用于指导精化的是伪区域的约束和伪区域语义中关键变量更好的界.
基于反例引导的抽象-精化方法还可用于训练和验证深度强化学习(deep reinforcement learning, DRL) 系统. Jin等人提出的TRAINIFY框架[92]可以在抽象的状态空间下训练出一个DRL系统, 当训练得到的DRL系统产生某种安全性质的反例时, TRAINIFY根据该反例优化抽象状态空间, 并在更精细的抽象状态上再次训练DRL系统. 通过重复以上过程就可以训练出一个精度高、鲁棒性好的DRL系统.
上述基于网络结构抽象和反例引导的抽象-精化方法通过将表现相似的神经元进行合并或删除, 减小网络规模, 然后利用现有的方法(SMT、MILP等)来验证神经网络的性质, 达到提高验证效率的目的, 最后得到的输出为神经网络可达集的上近似. 当对神经网络的结构抽象过于粗糙时, 此类方法会结合反例对抽象进行精化, 提高验证精度. 但是如何设定抽象神经元的标准以及如何达到精度与效率的平衡是此类方法的难点, 并且在抽象网络结构的过程中需要对神经网络重新编码, 时间代价比较高.
3.2.3 基于符号传播的验证方法基于符号传播的验证方法主要通过区间表示、线性松弛等方式, 将神经网络每一层之间的迁移关系表示为一系列符号约束并逐层传递, 最后得到输出层与输入层之间的约束关系, 再将输入层的数值边界代入符号约束关系中, 得到输出范围. 由于对ReLU等激活函数采取了线性松弛, 通常情况下, 此类基于符号传播的方法得到的输出范围也是神经网络可达集的上近似.
Gowal等人[34, 93]提出了由区间计算衍生而来的区间边界传播(interval bound propagation, IBP), 他们展示了如何利用IBP来训练可证明鲁棒性的大型神经网络, 这是一种可以用于训练分类器的不完备算法, 其主要思想是为神经网络中每一层神经元的多面体约束添加一个轴平行的上近似边界框(本质上类似于Box约束), 该边界框总是包含真实的多面体约束. 此方法相比于Wong等人[94]提出的基于对抗性训练的验证方法在扰动半径增大时有明显的竞争力.
Weng等人提出了一种与DeepZ类似的验证框架Fastlin[31], 可以求解
引理1 (Fastlin和DeepZ的等价性). 激活函数为ReLU的神经网络
证明: 设神经网络
| f(X1)=Wn⋅σ′n−1(Wn−1⋅σ′n−2(…σ′1(W1⋅X1+b1)…)+bn−1)+bn, |
其中, ·表示矩阵乘法, 对于Fastlin框架, 我们以求解输出层第
(1) 相同的Zonotope经过仿射变换之后, DeepZ和Fastlin的输出是等价的Zonotope.
(2) 相同的输入范围经过ReLU激活之后, DeepZ和Fastlin的输出范围相同. 注意, Fastlin只适用于ReLU激活函数的神经网络.
对于情形1, 由于神经网络在传播过程中交替进行仿射变换和ReLU激活, 为了简化计算, 我们先忽略表示层数的下标. 设第1层仿射变换的输入为
对于Fastlin输入范围中的任一点
下面证明情形2. 情形1的证明可得出对于每个神经元经过Fastlin和DeepZ的仿射层传播之后会得到相同的上下界
对于任意
综上所述, 可由归纳法证明出对于任意ReLU激活的神经网络, 如果神经网络的输入范围是Zonotope, 则经过Fastlin和DeepZ求出的输出范围是等价的.
Wang等人提出了Reluval[30], 这是一种基于符号区间传播的验证方法. Reluval为每一个神经元添加符号区间界, 类似于DeepPoly的符号界. 对于ReLU激活函数的模拟, 他们采用区间分割的方式, 将其中一部分神经元范围分割为若干个子区间的并集. 对于每个子区间, 该神经元很可能变成确定的激活或不激活的神经元, 从而得到更精确的输出范围. 相比于Reluplex等精确验证方法的高复杂度和难拓展性, 以及Wong等人[46], Dvijotham等人[70]提出的基于多面体松弛或凸优化带来的过度松弛问题, Reluval的区间计算能相对高效地传播, 同时他们通过切割输入区间尽可能避免过度松弛导致的假反例现象.
在接下来的工作中, Wang等人[32]在区间分析和线性松弛分析[30, 41]的基础之上改进了Reluval框架, 得到精度和效率都更高的验证工具Neurify. 相比于Reluval, 当神经元之间的依赖关系变得太复杂而无法进一步用符号表示时, Neurify通过添加一定的松弛来继续计算神经元的范围, 和DeepZ、Fastlin这两种验证框架有异曲同工之妙. 事实上, Neurify、DeepZ以及Fastlin在验证精度上是等价的, 而相比于Reluval和Reluplex, Neurify在效率和精度上都有明显的优势.
以上验证方法会面临如何将ReLU激活函数的松弛推广到tanh和Sigmoid等其他激活函数的问题, Zhang等人提出了通用的CROWN框架[33], 通过一种自适应的松弛方式为不同的激活函数添加符号线性边界来解决可拓展性问题. CROWN可以拓展到多种激活函数的神经网络上, 甚至可以采用二次函数为激活函数添加合适的松弛. 而对于ReLU神经网络来说, CROWN实际上和DeepPoly的精度是等价的. 相比于之前的方法, CROWN可以有效地验证规模超过一万个神经元、具有不同激活函数的神经网络. 随后Salman等人[95]提出了一个统一的分层凸松弛框架, 系统地阐述了DeepZ, Fastlin, Neurify, DeepPoly, CROWN等验证框架的关系, 从凸松弛和拉格朗日对偶这两个方面讨论了这些方法的验证效率, 并揭示了这类松弛方法在验证精度上具有的理论上限.
Li等人[36]和Yang等人[96]在符号区间算术的基础上, 进一步将符号传播和抽象解释结合, 将符号传播推广到更一般的数值抽象域上, 实现了工具DeepSymbol 和以此工具为基础的神经网络验证平台PRODeep[97]. 值得一提的是, PRODeep是国内首个神经网络验证平台, 它集成了约束求解、抽象解释和符号传播3类技术, 并对它们进行了深度的结合.
前述大多数工作重点关注结构简单的FNN的鲁棒性验证. Boopathy等人[35]提出了一个通用且高效的CNN-Cert框架, 将深度神经网络的鲁棒性验证拓展到了CNN, 可以处理包括卷积层、最大池化层、残差块等在内的多种神经网络结构, 并支持多种激活函数. CNN-Cert框架通过利用卷积层的特殊结构, 使得Fastlin和CROWN只是其特例, 并且在鲁棒边界相似甚至更好的情况下, 将二者的效率分别提升了17倍和11倍.
基于IBP的验证方法在许多种情况下的效率明显优于基于线性松弛的方法, 但IBP计算得到的边界要比线性松弛宽松得多. 因此Zhang等人提出了一种新的神经网络对抗训练方法, 通过将前向传播中的IBP边界和反向传播中基于线性松弛的CROWN边界相结合得到CROWN-IBP[37]. 他们构造出一个关于IBP边界和CROWN-IBP边界的损失函数, 通过最小化该损失函数求解出神经网络的参数, 使得训练之后的神经网络不仅具有良好的分类精度, 还具有较高的鲁棒性. 在训练可验证的鲁棒神经网络方面, CROWN-IBP具有很高的计算效率, 并且得到的范围始终优于直接利用IBP得到的范围, 很好地实现了精度和效率之间的平衡.
Lyu等人[38]在CROWN的基础上又提出了Fastened CROWN (FROWN)框架, 这是一种用于提高神经网络鲁棒性的训练方法. 他们证明如果将神经元的上下界约束个数分别只限制为一个, 则相比于线性规划, CROWN得到的神经元的上下界是最优的. 他们在此基础上提出的FROWN可以进一步地缩紧CROWN提供的边界, 并且在理论上能拓展到其他类型神经网络的验证方法中, 例如验证CNN的CNN-Cert以及验证RNN的POPQORN.
基于符号传播的验证方法将符号计算的高效、可拓展性等优势应用到神经网络验证中, 并取得了很多成果, 但是随着神经网络层数增加规模增大, 这类方法的表达式也会变得更加复杂, 并且在传递过程中会逐层放大误差.
3.2.4 基于Lipschitz的验证方法Szegedy等人[98]证明带有ReLU激活函数或者最大池化层等结构的FNN和CNN是Lipschitz连续的, 所以神经网络的输出在上下界范围内的所有值都是可达的. 因此一个比较自然的想法是从神经网络自身的性质出发, 利用Lipschitz常数来验证有关性质. 我们称一个神经网络具有Lipschitz连续性, 如果这个神经网络满足定义3[61].
定义3 (Lipschitz连续性). 给定两个度量空间
| dY(f(x1),f(x2))⩽KdX(x1,x2) | (1) |
其中,
关于Lipschitz验证方法, 比较早期的工作是Hull等人提出的[99]. 他们介绍了多项式神经网络(polynomial neural network, PNN) 验证技术, 使用Lipschitz常数为所有可能的输入提供神经网络输出的可保证边界, 从而避免了在所有可能的输入组合下测试网络的输出. Hein等人[52]提出了Cross-Lipschitz正则化函数, 利用局部Lipschitz常数, 给出了只具有一个隐藏层的神经网络的鲁棒边界. 但是该方法要求网络连续可微, 因此不能直接应用于ReLU神经网络.
Ruan等人利用神经网络输入和输出上的Lipschitz连续函数来解决神经网络的可达性问题, 提出了一种基于自适应嵌套优化的新算法DeepGO[64], 并且证明了ReLU之外的其他激活函数, 例如Softmax、Sigmoid以及tanh等也具有Lipschitz连续性. 他们将神经网络的可达集分析转化为求解神经网络的全局最大/最小值, 进一步转化为一系列优化问题并迭代求解, 还利用Lipschitz常数
Weng等人进一步为神经网络的鲁棒性分析问题转化为局部Lipschitz常数的估计问题提供了理论依据, 并通过极值理论对Lipschitz常数进行了有效的评估, 他们首次提出了鲁棒性度量分数Clever (cross Lipschitz extreme value for network robustness)[53], 并且可以应用到ImageNet等大型数据集相关的神经网络分类器. 虽然没有提供严格的保证, 但Clever分数确实是一个很好的鲁棒性估计, 并且在FNN中与Reluplex给出的精确鲁棒边界是比较接近的. 相比于其他的神经网络验证方法, Clever具有以下优势: Clever分数与攻击方法无关, 并且可以不受神经网络结构的限制, 对于规模庞大、结构复杂的神经网络来说是一个很好的衡量鲁棒性的方法.
Weng等人在随后的工作中[100]对Clever提出了两个方面的拓展, 其一是利用极值理论为二次可微的分类器, 即带有Sigmoid、tanh、Softplus等激活函数的神经网络提供了一种鲁棒性估计, 称为二阶Clever分数. 其二他们阐述了如何利用Clever分数和反向传播可微近似(backward pass differentiable approximation, BPDA)[101]来处理梯度掩码(gradient masking)[101, 102]之后的不可微变换, 然后借助Clever评估模型的鲁棒性. 梯度掩码是一种流行的防御方法, 典型的梯度掩码方法包括添加不可微层、防御性蒸馏[103]等. 他们发现在许多种情况下, 神经网络的一阶和二阶Clever分数是一致的, 因此Clever作为神经网络的鲁棒性衡量指标, 是比较合理且可拓展的.
前述Clever[53]工作中还提出局部Lipschitz常数可以看作是方向导数的最大范数, 因此Weng等人提出了Fastlip[31], 通过分类讨论ReLU神经网络的3种激活模式推导出局部Lipschitz常数的上界, 从而获得扰动区域的鲁棒边界. 他们实验发现由Fastlip得到的鲁棒边界相比于Reluplex得到的精确边界仅松弛2–3倍, 并且与基于线性规划的方法相比, 也具有非常接近的精度. 但是由于他们不需要求解任何的线性规划问题或者对偶问题, 因此在时间效率上要快33–14000倍. 当验证ResNet等大规模神经网络时, Fastlip仍然能给出不平凡的鲁棒边界.
此类基于Lipschitz常数的验证方法通常效率非常高, 与精确的验证算法相比, 效率可达到其成千上万倍. 但是由于这类方法求解得到的鲁棒半径非常依赖Lipschitz常数的求解精度, 因此如果Lipschitz常数精度不高很可能导致这些验证方法的鲁棒半径不准确, 从而难以验证一些比较强的性质. 并且由于Lipschitz常数仅是对鲁棒半径做出一个估计, 许多基于Lipschitz常数的方法并没有一个严格的鲁棒性保证.
3.2.5 基于凸优化的验证方法基于凸优化的神经网络验证方法主要是利用对偶理论、半定规划等数学原理来优化神经网络的鲁棒边界, 以及通过最小化损失函数来训练一个可证明鲁棒性的神经网络, 此类验证方法的数学理论较强.
Dvijotham等人[69]基于线性规划提出了一种算法框架来训练可证明鲁棒性的神经网络, 从而验证网络是否满足给定的输入-输出特性. 该算法的关键思想是同时训练两个网络, 一个预测器网络用于当前任务的预测, 另一个验证器网络用于计算预测器网络满足被验证属性的程度. Dvijotham等人[70]在后续的工作中将验证问题转化为一个凸优化问题, 寻找违反性质的最强反例, 并通过求解这个凸优化问题的拉格朗日松弛来刻画最坏情况下关于给定性质的鲁棒半径. 该框架可以应用于具有任意类型激活函数的FNN, 并且凸优化问题的规模与神经元的个数呈线性相关, 因而复杂度较低.
Wong等人[46]将FNN的扰动区域定义为一个凸多面体, 通过对激活函数的可达集添加一个凸外部逼近(convex outer approximation), 并通过线性规划最小化该外部逼近在最坏情况下的损失. 他们证明出该线性规划的对偶问题可以近似地表示为反向传播的深度网络, 从而高效地找到一个可证明的鲁棒边界, 以及潜在的对抗性样本. 他们提出的方法可以训练一个鲁棒的ReLU深度神经网络分类器, 并且可以抵御任意类型的攻击.
在后续的工作中, Wong等人[94]将上述基于凸优化的方法拓展到了其他非线性激活函数以及带卷积层或残差结构的神经网络中, 并且可验证的网络规模也有了很大的提升. 虽然还不能达到ImageNet这样的验证级别, 但是在规模和可拓展性上相比于前面的工作有了实质性的进展. 他们主要对前面的工作[46]进行了几点扩展: (1) 通过激活函数的Fenchel共轭函数拓展到具有任意激活函数的神经网络结构中; (2) 使用非线性投影技术, 对网络的输入维数和隐藏神经元的个数线性缩放, 同时最小化精度损失. 这个工作标志着深度防御的可拓展性向前迈出了重要的一步, 但他们提到仍有一些值得改进的地方: 除了利用有界的范数攻击来描述鲁棒性之外, 还可以进一步地考虑对抗扰动的性质.
Raghunathan等人[71]提出了一种基于半定规划(semidefinite programming, SDP) 的验证方法来计算具有一个隐藏层的神经网络在最坏情况下的鲁棒边界, 该边界可以为网络输入的所有攻击提供鲁棒性证书. 他们利用这个鲁棒性证书的可微特性, 通过对网络参数的联合优化, 提供了一个自适应的正则化器, 可以对所有类型的攻击提供鲁棒性保证. 实验表明基于SDP的方法得到的鲁棒边界相比于基于Frobenius范数和基于谱范数得到的边界更加严格.
Raghunathan等人在随后还提出了一种更紧的基于SDP的方法来证明具有ReLU函数的神经网络的鲁棒性[104], 并且可以拓展到具有任意多个隐藏层的FNN当中. 相比于其他凸优化方法, 例如Wong等人[45]以及Dvijotham等人提出的方法[69, 70], 他们提出的SDP松弛可以捕获到神经元之间的关联信息, 得到更紧的边界. 此外, 相比于他们之前的工作[71], 该工作中提出的SDP松弛能提供更严格的鲁棒性保证. 在可拓展性方面, 新的SDP方法理论上可以应用于CNN, 只需将其展开为FNN即可, 但是还没有进一步的实践和验证.
Müller等人提出了一种基于凸优化的PRIMA框架[47], 在基于抽象解释的k-ReLU的基础上进一步提升了验证精度. PRIMA的主要亮点在于SBLM (split-bound-lift method)的全局验证框架, 并利用一种称为PDDM (partial double description method)的对偶方法求解多面体的凸包, 在最坏的情况下求凸包也能达到多项式复杂度. 实验表明他们的方法相较于目前主流的验证算法, 如DeepPoly, k-ReLU等, 都有不错的提升. 他们在实验中利用英伟达公司自动驾驶系统装载的神经网络Dave[7]来测试验证算法的精度和效率, 是神经网络鲁棒性验证应用于工业系统中大型神经网络的一个进步.
以上基于凸优化的思想验证神经网络的方法, 相比于其他基于抽象解释、Lipschitz的方法在验证规模上稍为逊色, 难以拓展到识别ImageNet等大型数据集的神经网络上. 但是这类方法通常可以帮助训练出一个具有良好对抗鲁棒性的神经网络, 并且部分验证方法可以支持多种激活函数的神经网络验证, 是数学理论在形式化验证领域中的一个很好的应用.
表 3对各类FNN验证方法的优缺点做出了对比, 更多关于FNN验证的文章可以详见文献[105,106]. 文献[102]重点介绍了神经网络的验证、测试、攻击防御、可解释性等相关工作, 另外文献[107]详尽地介绍了关于FNN的鲁棒性分析方法, 本综述则从时间维度上展示了各类FNN、RNN验证方法的发展, 分析了更多关于RNN验证方法以及FNN、RNN验证方法之间的联系.
| 表 3 FNN、RNN典型验证方法类别的优缺点比较 |
RNN在自然语言处理和语音识别等领域应用广泛, 它以时间序列数据作为输入, 由于其内部具有循环结构, RNN会将循环状态不断地向自身传递, 最终得到输出. 对于分类RNN来说, 输入可能是一系列待分类的图片序列, 输出为图片的预测标签. 而对于用作自动驾驶控制系统的RNN, 则会以一系列连续的道路探测图像作为输入, 处理之后输出对车辆的控制信号, 例如直行, 转弯, 减速等. 目前应用比较广泛的RNN包括Vanilla RNN[108], 长短期记忆模型(long short-term memory, LSTM)[109], 门控循环单元(gated recurrent unit, GRU)[110]等.
Vanilla RNN是结构最简单的RNN, 接收序列输入, 最后输出预测值, 与FNN结构类似, 不同之处在于每一个隐藏状态的值将由上一个隐藏状态与这一时刻的输入决定.
LSTM首次由Hochreiter等人[109]提出并被广泛应用于不同的领域, 例如自然语言处理[111, 112], 阅读理解[113, 114], 聊天机器人[115]等, LSTM提出的主要目的是用以解决在长序列训练过程中存在的梯度消失以及梯度爆炸问题. 不同于FNN, LSTM网络具有记忆性和遗忘性, 因而对于一些较长的序列, LSTM能表现出优异的处理能力. 如果将LSTM网络展开, 则其是由一系列具有重复结构的链式模块构成的. LSTM在每个模块中都通过3个门来添加或删除信息, 分别称为忘记门、输入门以及输出门. 门的结构即为Sigmoid激活操作和哈达玛(Hadamard)积
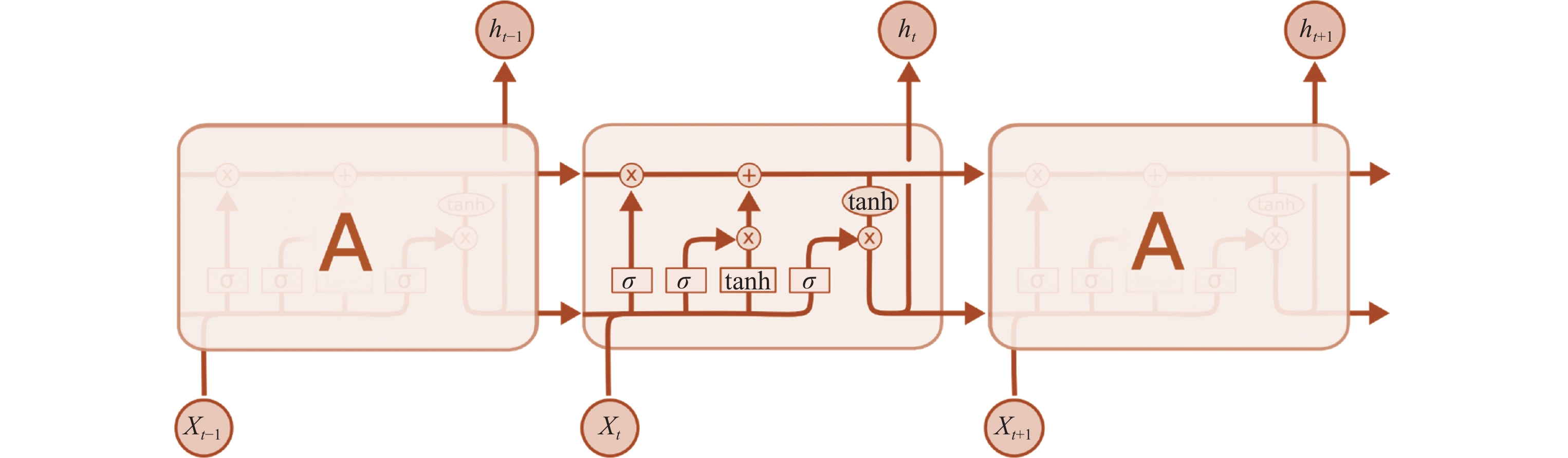
|
图 5 LSTM的结构 |
门控循环单元(GRU)的概念是由Cho等人[110]提出来的, 作为LSTM网络的变体, GRU拥有更简单的结构以及更优越的效果, 因此在自然语言处理领域中也得到了广泛的应用. GRU的结构包括重置门和更新门, 如图 6所示, 其中方框表示激活函数操作, 圆圈表示圈内运算符的逐点操作, 箭头表示数据的流向.

|
图 6 GRU的结构 |
由于目前RNN验证方法正处于起步阶段, 大多数验证方法都从Vanilla RNN的验证入手, 再将其拓展到目前应用最为广泛LSTM网络, 第5节将具体地介绍和分析RNN的验证方法.
5 RNN验证方法RNN的循环单元是为了处理序列输入, 使得序列中下一个元素的处理过程依赖于前面元素的处理结果, 多被用于自动驾驶中的车轨预测、语音识别、机器翻译以及其他依赖于序列输入的领域. 由于结构上和FNN有显著不同, RNN对于序列数据的扰动空间存在更严格的定义, 并缺乏适当的度量扰动程度的指标, 因此相比于FNN, 此类序列扰动空间是更加难以描述的[117]. 因此, 尽管目前FNN的鲁棒性验证的研究已经取得了很多进展, 但FNN的验证方法并不能完全适用于RNN验证. 对RNN验证方法的研究目前仍处于起步阶段, 相关的工作还比较匮乏.
目前已有的文章中关于RNN的鲁棒性验证主要分为3大类: 一类是基于抽象解释[118]的方法, 将RNN的输入范围

|
图 7 RNN验证方法, 不同的颜色代表不同验证技术类别 |
基于抽象解释的验证方法在FNN上得到了较为成熟的应用, 一个自然的想法便是将抽象解释框架应用到RNN验证领域中. 因为很难形式化地定义RNN在语言预测方面的错误, 因此目前相关工作的验证对象主要被限制在用于分类任务的RNN中.
当前有许多通过攻击RNN来评估鲁棒性的工作[119, 120], 以及将Clever分数[53]直接应用于RNN, 为RNN提供鲁棒性分数来衡量鲁棒性等, 但是这些方法并没有严格的鲁棒性保证. 受到Fastlin[31]为神经网络的操作添加线性约束的启发, Ko等人首次将抽象解释与RNN验证结合起来提出了POPQORN[54]验证框架, 这也是首次提出的RNN的验证工作. 具体地, 当输入产生一个
他们采用线性函数或线性平面逼近非线性函数, 并基于梯度优化来计算相应的线性函数的参数. 由于优化过程需要较高的计算复杂度, 因此POPQORN很难扩展到包含成千上万个神经元的神经网络中. POPQORN能验证的Vanilla RNN的神经元个数约为896个, LSTM网络神经元个数约为512个, 离拓展到更大的网络还有一定的距离. 其次, 由于优化方法缺乏最优性保证, 线性边界的系数很可能不精确. 如果平面和真实的曲面之间间隙过大, 可能会导致给出的线性边界过于松弛, 以至于能验证的鲁棒半径比较小. 一个可能的改进方向是考虑构造一个损失函数, 尽可能减小线性平面与真实非线性函数之间的差距.
Du等人将DeepZ的思想应用到了RNN验证中, 提出了一种比POPQORN更紧的验证框架Cert-RNN[55]. 类似于DeepZ, 他们定义了一个Zonotope去捕获对抗性输入的范围, 为tanh等非线性激活函数构造Zonotope上近似, 并将该Zonotope在神经网络中逐层传递. 而中间的仿射变换层不改变Zonotope精度, 最后验证输出Zonotope是否满足给定性质. 他们为Sigmoid和tanh等非线性激活函数采用的松弛方式比DeepZ更加精确: 连接自变量

|
图 8 Cert-RNN和DeepZ在tanh函数上的Zonotope松弛对比 |
在LSTM网络中, 如果采用POPQORN中的方法, 为Sigmoid
相比于POPQORN验证框架, Cert-RNN具有两个主要的优势: 首先, 由于POPQORN采用了不精确的区间计算, 利用体积最小化将线性平面系数求解的问题转化为带约束的优化问题, 效果可能不稳定, 并且没有最优性保证. 而Cert-RNN采用了Zonotope描述神经元之间的联系, 对非线性激活的松弛理论上会更精确. 这就是Fastlin和DeepZ在FNN验证上效果一致, 而它们在RNN上面的扩展工具POPQORN和Cert-RNN精度有差异的原因. 其次, POPQORN采用梯度下降法逼近优化问题的解效率低下, Cert-RNN利用了抽象变压器来松弛非线性操作, 可以比较高效地验证RNN的鲁棒性. 在一些LSTM网络中, Cert-RNN的验证效率比POPQORN高20倍以上.
在FNN的鲁棒性验证中, 以DeepPoly为原型的反向传播框架是一种比较主流的验证方式. 为了将反向传播的思想应用到RNN验证中, Ryou等人将DeepPoly框架[27]与RNN验证相结合, 提出了新的验证理论: Prover[56]. 他们借鉴了DeepPoly的思想, 为RNN的每一个神经元添加数值界和符号界作为抽象域. 对于非线性激活函数以及非线性操作, 他们仍然采用线性函数为神经元添加上下界约束. 与POPQORN框架不同的是, 他们通过在自变量的可行域内采样, 将采样点与其在线性平面上投影的距离之和作为损失函数, 通过求解最小化损失函数得到的线性规划问题, 解得线性约束的系数, 如图 9所示. 他们在激活函数曲面上随机采点并投影到线性平面上, 以原始采样点和投影点的距离之和作为损失函数并将其最小化求得线性平面系数. 他们还提出将原始的可行域分为4个不同的三角形区域, 在每个区域分别采样求解出该区域对应的“候选平面”, 并利用这些候选平面的线性组合去拟合原始的非线性函数. 在计算非线性激活函数的线性上下界时, 由于Prover是根据可行域中采样的点集来计算线性边界的系数, 所以求出来的线性平面可能不具有可靠性. 为了解决这个问题, 他们通过平移线性边界的系数来调整上下界, 得到一个可靠的线性边界.
|
图 9 Prover求解线性函数系数的方法示意图 |
实验部分对用于语音分类及图像识别的LSTM进行验证, 并和POPQORN进行了比较, 结果表明用各子区域的候选平面做线性组合的方式优于直接在整个可行域上的线性平面拟合, 并且这两种方法能验证的半径都要远远优于POPQORN.
以上的RNN验证方法都是基于抽象解释, 将RNN的输入和中间操作都用线性约束为其添加一个上近似, 最后验证输出的线性区域是否满足性质. 基于抽象解释验证RNN的方法大多借鉴了FNN的验证方法, 关系如后文图 10所示. 其中不同颜色表示不同的验证方法类别, 箭头表示被指向的方法由箭头出发的方法借鉴而来.
|
图 10 RNN验证与FNN验证的关系 |
另一种常见的RNN验证方法是将RNN展开为等价的或上近似FNN, 再验证该FNN的性质.
最早研究此类验证方法的工作是Akintunde等人提出的RNSVerify[57], 这是针对基于RNN的闭环系统的形式化验证方法. 基于RNN的闭环系统(RNN-AES)是基于FNN闭环系统[121]的扩展, 是由一个环境和一个代理(agent)组成的闭环系统, 该环境包含若干状态, 并由该代理来更新当前的状态. 此时代理由RNN来充当, 并根据当前的环境选择下一个操作来更新状态. 他们形式化地定义了RNN-AES闭环系统, 并引入了若干支持该闭环系统的语义, 用BNF公式定义出需要验证的性质或规范, 便于解决由此产生的验证问题.
RNSVerify用两种方式将RNN展开为FNN, 其一是IOS (input on start)展开方法. 展开之后FNN的输入为原RNN在所有时间步的输入, FNN第1层的权重矩阵即为RNN每个时间步的输入到隐藏层系数矩阵
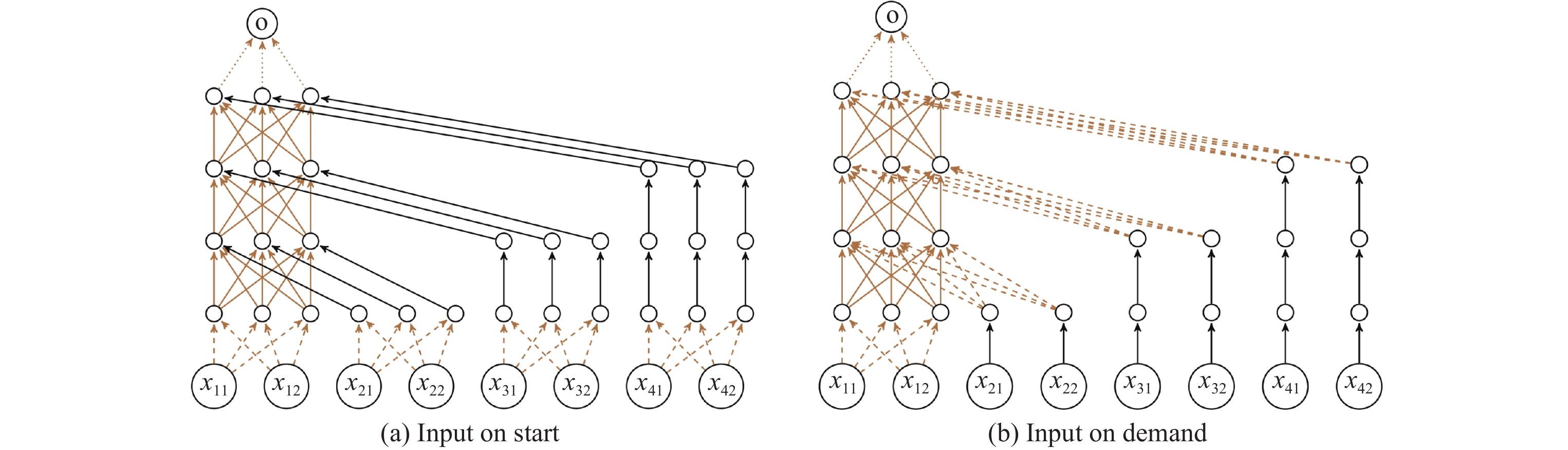
|
图 11 IOS展开方法和IOD展开方法 |
他们将展开得到的等价FNN编码为MILP约束, 并对AES系统环境中的状态和迁移规则用线性约束表示, 将问题编码为布尔可满足性问题(Boolean satisfiability problem, SAT) 来判断系统是否满足给定的性质. 如果该AES系统满足给定的性质就输出True, 否则算法会给出反例. 该方法对复杂程度有限的控制器是可靠且完备的. 他们利用OpenAI中的钟表垂直摆动作为实验, 目标是让代理学习如何通过在每个时间步施加一个小的旋转力来保持钟摆直立. 他们对IOS和IOD两种展开方法进行了比较, 发现IOD在MILP编码的过程中需要的变量和约束个数更少, 所以在验证时间上相比于IOS具有明显的优势.
实验中用于控制的RNN仅包含16个隐藏单元, 规模远小于其他RNN验证工具能验证的神经网络. RNSVerify通过展开RNN并利用线性规划来求解约束可满足性问题. 这种白盒验证方法非常依赖于RNN内部结构以及权重矩阵等参数来生成FNN, 因此不能验证任意序列长度和更灵活的属性. 由于将RNN展开为FNN的过程中神经元的个数会扩增若干倍, 在进行MILP编码时会导致变量和约束个数激增, 所以将该验证方法拓展到更复杂的AES系统存在瓶颈.
Zhang等人[58]在RNSVerify的启发下也采用了展开为FNN的方法来验证RNN, 他们采用了3种已有的验证方法来验证展开之后的RNN: 多面体传播, 并利用MILP编码ReLU激活函数[67]、基于反例引导的抽象-精化方法(CEGAR)以及不变量探测. 与前面介绍的RNN鲁棒性验证方法不同的是, 他们介绍了一种认知任务——随机点运动任务, 目的是在有噪声的环境下使人或动物做出决策. 他们将该认知任务应用于RNN, 并训练RNN使其对噪声环境下的运动点做出正确的决策. 他们提出了该任务下的3种可能满足的性质, 并对其进行验证: (1)如果给定的刺激措施足够强烈, 网络应该会输出正确的决策; (2)在刺激过程中出现了与其他刺激点不一致的点, 检验这个点的特征是否会诱导RNN选择这个极端点的方向; (3)检验是否存在一个输入, 导致最后几步的输出状态产生强烈的震荡, 做出相反的决策. 他们在验证以上3种性质时, 固定了RNN的输入长度, 从而可以将该RNN展开为FNN进行验证.
他们在固定输入长度(110步长)后将RNN展开为FNN, 并利用前述3种验证方式, 分别在30个输入区域中验证上述性质, 并与参照方法NNV[122]进行了对比实验. 他们的创新点在于对一些RNN的应用场景提出相应的性质并验证其是否成立.
Jacoby等人对展开神经网络的方法做出了改进, 提出了工具RnnVerify[59], 其基本思想也是将RNN展开为FNN. 与上述方法不同的是, 他们用不变量推理从原始的RNN得到FNN, 作为原始RNN的上近似, 然后用Marabou来验证FNN. 他们对于单个记忆单元和多个记忆单元的网络分别介绍了不变量的生成方法. 对于单个记忆单元, 采用形如
以上内容都是基于将RNN展开为FNN的验证方法. 当限制输入序列长度时, RNN中隐藏单元的循环次数也随即确定, 因此可以利用直接展开法得到等价的FNN, 或者利用不变量探测的方式展开得到一个上近似FNN, 再利用现有的验证FNN的方法进行验证. 虽然可以利用现有的工具验证展开之后的RNN, 但由于展开为FNN的过程会导致参数个数扩大数倍, 将FNN编码为MILP或者利用Marabou验证的时间复杂度不容小觑.
5.3 基于自动机的验证RNN可以用于处理序列输入, 所以一种自然的验证方法便是将RNN转化为确定型有限自动机(deterministic finite automaton, DFA)[123, 124], 并借助适当的自动机检验工具[125]对所提取的自动机执行验证任务. 从RNN中提取有限自动机可以采用白盒学习算法来实现. 例如Weiss等人[126]提出利用L*算法, 用RNN来回答等价查询以学出一个近似的DFA
在验证RNN的过程中会存在一些问题, 例如在RNN中对序列数据的扰动空间以及对扰动程度的刻画缺乏适当的度量. 为了解决这些挑战, Wang等人[117]通过对字符串定义平均编辑距离来度量字符串之间的扰动程度, 并使用DFA来检查生成的对抗性样本是否违反了某些性质. 他们基于量化分析从给定的RNN中提取出一个DFA[131, 132], 在此基础上形式化地定义了一系列指标(正确率, 成功率, 保真度等)来刻画提取出来的DFA的质量, 然后利用随机采样的方法验证提取出来的自动机. 他们在Tomita语法上展示了用不同的RNN (二阶RNN[133], Elman-RNN, MI-RNN, LSTM以及GRU等)提取出来的DFA的准确率, 成功率以及保真度等性质, 并发现具有二次型形式的二阶RNN能更高效更精确地提取自动机. 他们利用提取出来的DFA验证RNN的对抗鲁棒性, 此处的鲁棒性用
| γ=#{1⩽j⩽T:f(xj)=A(xj)=p}T, |
其中,
这种通过在扰动区域内随机采样来估计神经网络的鲁棒性质的方法, 不能为神经网络提供一个严格的概率鲁棒保证. 如果输入空间的维数过高就很可能导致采样数不够充分, 因此进一步影响对抗鲁棒性估计的准确性.
不同于随机采样验证对抗鲁棒半径, Vengertsev等人[61]用蒙特卡洛采样法来检验他们形式化定义的6种性质, 包括4种状态安全性质: 高置信度、决断性、鲁棒性和覆盖性, 用来描述理想的RNN应该具有怎样的结构或参数; 以及2种时序安全性质: 长期关系和记忆性, 用以描述RNN在处理输入序列中的每个元素后, 之后的输入序列应满足的条件. 他们用标签状态迁移系统(labeled transition system, LTS)[134]来描述RNN的行为. 在这个状态迁移系统中, RNN模型的以上6种性质被定义为线性时态逻辑LTL公式, 然后对该有限状态系统的行为进行形式化推理.
Vengertsev等人[61]假定待验证的系统有许多违反属性的路径. 为了完整刻画待验证模型的性质, 他们利用蒙特卡洛采样法来估计两个隐藏神经元个数分别为80和240的RNN模型
在实际应用中, 基于从RNN提取自动机的验证方法存在一些缺点: 其一是状态爆炸, 即从RNN中学习到的DFA可能太大, 无法显式构造. 另外, 由于RNN比自动机更有表现力, 从RNN提取到的自动机实际上不能完全刻画RNN的行为. 因此在自动机上的反例不一定是RNN的真实反例, 此类提取近似自动机的验证算法是不完备的. 并且前述的文章中并没有定量评估DFA描述RNN实际行为的准确性. 此外, 这种从现有的RNN中提取自动机的方法通常只能验证一些正则性质, 存在一定的局限性.
相比于上述两种通过采样的方式来粗略估计RNN模型满足性质的概率, Mayr等人[62]给出了性质的概率保证. 他们提出了一种基于黑盒模型和有界L* (bounded-L*)算法[135]的动态学习方法来验证RNN的各种性质, 并为模型提供了概率保证. 具体地, 若想验证一个RNN
虽然在运行有界L*算法时, 也无法保证学出的自动机
Khmelnitsky等人[63]讨论了二分类RNN相关的验证问题. 假定RNN
不同于传统的模型检测, 这种将自动机学习与模型检验结合起来的方法总是可以产生一个反例数据流, 其刻画了反例的一般特征. 并且他们提出的PDV验证方法是黑盒验证方法, 不需要知道RNN的结构, 规避了RNN结构带来的复杂度很高的问题. 但因其结合了L*算法和随机采样验证性质的SMC算法, 相较于简单的SMC算法, 复杂度往往更高.
考虑基于自动机提取来验证RNN是一种自然的想法, 提取自动机的过程可以利用很多现有的成熟的算法, 例如L*算法以及其他量化分析的提取方法. 此类验证算法大多用采样的方式验证自动机满足某种性质的概率, 不能对性质提供一个概率保证.
6 RNN应用场景中的其他性质验证Mayr等人[62]将黑盒验证和L*算法结合起来, 通过对性质的补
目前RNN大多数待验证属性都是学术界定义的, 和工程实践中所需要保证的性质可能存在不小的差别. 为了缩短理论研究和实际应用的距离, 考虑RNN在实际应用中的性质很有研究价值.
近日, Bacciu等人[137]提出了RNN网络在大型实际应用场景下, 特别是自动驾驶领域中相关性质的验证. 他们提出, 验证基于RNN的决策系统可以由以下3个步骤组成: ① 利用POPQORN对RNN输入的扰动进行鲁棒性评估; ② 根据步骤①的鲁棒性验证结果, 设计一个由RNN和若干个冗余系统以及比较系统构成的评估系统. 冗余系统可以是与RNN系统输入相同的不同算法, 也可以是具有不同技术(例如雷达或激光雷达)的算法和传感器系统. 在基于RNN的系统和冗余系统计算出它们的输出数据之后, 比较系统负责对所取得的结果进行比较, 并基于RNN系统的输出是否可信来定义一套适当的安全措施, 即鲁棒性较差的模型需要更强的措施来避免灾难发生; ③ 根据“预期功能安全(SOTIF)指南”对整个系统的功能进行广泛测试与验证, 并评估适当的安全性能指标, 根据确定的评估指标和相应的阈值, 以及测试长度来验证整个系统. 但他们仅在理论上提出了RNN在实际验证中面对的挑战的解决方法, 并未对测试用例进行实验, 可见验证实际应用中大型神经网络的安全并非易事.
RNN在图像处理、数据分类、语音识别以及自治系统中作为控制器等方面应用广泛. 而在实际环境中, 通常需要部署在资源受限的平台(如移动电话或嵌入式设备)上, 这些部件的内存占用和能耗便成了瓶颈问题, 所以人们的关注焦点转移到了利用一些启发式技术对这些RNN
定义4 (RNN的等价性). 两个RNN
DiffRNN也可以应对RNN中的非线性激活函数Sigmoid和tanh的计算、长序列的输入以及门与状态之间的交互问题等挑战, 可以较为准确地刻画两个RNN之间输出的差距.
实验部分在Vanilla RNN和LSTM网络上与POPQORN做出了对比, 其中LSTM的规模最大为
研究人员也提出了很多用于自然语言处理(natural language processing, NLP) 的RNN验证工作. 例如Zhang等人[139]开发了一种提高RNN对抗任意字符串变换的鲁棒性训练方法, 产生的模型对字符串变换的攻击方式有更强的鲁棒性. Dong等人[140]提出了对抗单词变换的鲁棒性训练方法, 他们将单词替换的攻击空间建模为一个凸包, 利用正则化项对实际的替换进行扰动, 并结合对抗性训练来提高鲁棒性. Xu等人[141]开发了一个对任何神经网络结构进行扰动分析的自动化分析框架. Shi等人[142]提出了一种结构类似于RNN的Transformer的验证方法等等. 更多关于NLP领域模型的对抗攻防和鲁棒性分析方法可以参考文献[143, 144].
7 神经网络的其他鲁棒性质验证在前面的章节中, 我们详尽地介绍了FNN和RNN局部鲁棒性的验证方法, 而除了局部鲁棒性之外, 目前的研究还包括一些全局鲁棒性和概率鲁棒性验证的工作. 公式(3) 展示了全局鲁棒性、概率鲁棒性和局部鲁棒性等安全性质之间的关系:
| 安全性=(可达集⊨性质P?){鲁棒性{局部鲁棒性全局鲁棒性概率鲁棒性其他性质 | (2) |
局部鲁棒性仅体现出神经网络在单个样本上抗干扰的性质, 而全局鲁棒性(global robustness) 可以刻画出神经网络在整个输入集合中不同类别之间的稳定性. 我们采用文献[145]中定义的全局鲁棒性. 在此先定义符号
|
图 12 全局鲁棒性示意图 |
定义5 (全局鲁棒性). 给定一个神经网络
| ∀x1,x2∈X,‖x1−x2‖p⩽ϵ⇒Cf(x1)⊥=Cf(x2). |
关于全局鲁棒性验证的工作目前比较少, Ruan等人[146]将神经网络的全局鲁棒性定义为测试数据集上最大鲁棒半径的期望, 并开发出了高效的验证算法; Yang等人[96]提出了首个具有严格可靠性保证的全局鲁棒性高效验证算法; Sun等人也提出一种全局鲁棒性的验证方法DeepGlobal[147], 可以展示出FNN的决策边界. 通过这些边界可以帮助搜索神经网络的对抗性危险区域(adversarial dangerous regions, ADR), 即容易受到微小对抗性扰动影响的输入区域.
要保证样本
定义6 (概率鲁棒性). 给定一个神经网络
| P({x∈Bp(x0,r)∣Cf(x)=Cf(x0)})⩾1−ϵ, |
则称神经网络
注意, 本文中讨论的神经网络f均是连续函数, 因此其必然是Borel可测函数. 相比于局部鲁棒性, 概率鲁棒性的验证在实际应用中也是不可或缺的, 例如在自动驾驶安全标准中通常会使用事故率来衡量自动驾驶车辆的安全性[148]. 在神经网络的概率鲁棒性验证方面, 比较有代表性的工作为Baluta等人提出的PROVERO工具[149], 将待验证的模型视为黑盒, 并基于输入空间的分布进行采样来确定神经网络的概率鲁棒性, 该算法能在1 h内验证ImageNet数据集相关的VGG16、ResNet50等大型网络的概率鲁棒性质. Li等人指出, 概率鲁棒性对于输入维度很高的深度神经网络(如图像分类任务的神经网络)和严格意义上的局部鲁棒性往往差别很大, 不能真实体现神经网络在实际使用中的鲁棒性质, 并进一步提出了概率近似正确模型鲁棒性(PAC-model robustness)的概念[150], 从而通过模型学习更好地刻画高输入维度的深度神经网络的概率鲁棒性. 其他概率鲁棒性的验证工作还包括文献[151, 152]等.
8 未来的研究方向本文主要介绍了FNN和RNN的鲁棒性验证相关的研究, 并探讨了二者之间的内在联系. 我们通过分析发现目前学术界对FNN的局部鲁棒性验证方法层出不穷, 而对于RNN鲁棒性质的研究和其他类型鲁棒性质的验证还处于起步阶段, 相关的验证方法目前还比较少. 然而从整体上看, 目前这些形式化验证方法能处理的神经网络规模可以拓展到VGG、ResNet等大型网络, 但是对工业界中的大型复杂系统的验证仍然存在瓶颈. 为了神经网络的鲁棒性验证领域的进一步发展, 我们归纳得出几个未来可行的研究方向.
● 研究局部鲁棒性之外的其他性质, 例如概率鲁棒性、几何鲁棒性、公平性、安全性、可解释性等. 目前验证神经网络鲁棒性的研究主要集中在基于
● 换一种角度验证神经网络. 不管是神经网络的鲁棒性验证还是程序正确性分析, 其本质上都属于模型检验领域, 因此Liu等人[158]另辟蹊径, 从模型检验的角度出发, 对ReLU激活的神经网络提出了一种ReLU时序逻辑(ReLU temporal logic, ReTL) 并定义了相关的语义, 对神经网络的可达性等性质进行验证, 是一种非常新颖的验证模型鲁棒性的方法. Guo等人[159]从分治算法的角度, 提出了基于分类置信度排序的神经网络鲁棒性验证方法, 将神经网络鲁棒性验证问题转化到若干定向类型验证的子问题, 有效提升了多个开源验证工具的鲁棒性证伪性能. 因此, 从不同的角度验证神经网络的鲁棒性也会有很大的发展空间.
● 研究其他类型神经网络的鲁棒性. 在大型的工业系统包括运用比较广泛的神经网络除了深度神经网络和RNN之外还有CNN和图网络等. 深度神经网络的鲁棒性验证已经有了比较丰富的研究, 但其他种类的网络鲁棒性研究比较少, 仍然有很大的研究空间. Zhang等人[160]提出了以Swish函数作为激活函数的神经网络的鲁棒性验证方法, 他们利用线性逼近技术将鲁棒性验证问题转化为约束求解问题, 并对非线性激活函数进行线性逼近, 进一步验证Swish神经网络的鲁棒性. Zhang等人[161]提出了一般量化神经网络(quantized neural network, QNN) 的MILP建模方法, 并基于此设计了一般量化神经网络鲁棒性分析框架, 实验结果显示比此前基于SMT的鲁棒性验证方法在效率上具有明显的优势.
● 研究大型智能系统的安全性. 目前神经网络被广泛应用于安全攸关系统中, 例如自动驾驶, 飞机巡航控制等, 保证神经网络组件的安全性或者鲁棒性并不足以保证整个智能系统的安全性. 对智能系统整体的安全性研究已经存在不少工作, 包括Dreossi等人提出的VerifAI[162, 163]工具, Kazak利用深度神经网络验证相关思想, 提出了一种验证深度强化学习(deep reinforcement learning, DRL) 系统的验证工具Verily[80], Zhou等人为多智能体学习框架MFAC提出了一个鲁棒性训练框架RoMFAC[164], 使其具有良好的对抗鲁棒性, 以及其他的智能系统验证工具NNV[122], Percemon[165]等, 对自动驾驶和无人机的运行场景进行验证. 因此, 对此类智能系统的鲁棒性、安全性验证也有很大的发展空间.
9 结 语神经网络的鲁棒性研究在形式化验证领域正处于快速发展的时期, 随着越来越多的智能系统应用于现实生活, 神经网络的鲁棒性验证也将变得更加重要. 虽然FNN的鲁棒性研究工作林林总总, 但是目前的研究仍然停留在中等规模的网络上验证精度与效率的权衡, 而难以拓展到实际应用中的大型神经网络中. 并且除了局部鲁棒性, 全局鲁棒性和概率鲁棒性等其他鲁棒性质的验证工作目前还比较匮乏. 同时, 我们对神经网络的预测机制和原理仍然不甚了解, 难以将这些形式化的验证方法应用于工业界含有神经网络等智能组件的大型智能系统中. RNN因为具有更复杂的结构, 研究其局部鲁棒性的工作目前仍比较少, 能验证的神经网络规模仅包含几百上千个神经元. 本文分析了大量的FNN和RNN验证的相关文章, 目的是梳理FNN和RNN验证方法的发展现状, 并揭示两种神经网络鲁棒性验证方法之间的内在联系. 我们在最后探讨了神经网络的一些其他鲁棒性的定义与验证方法, 以及神经网络鲁棒性验证领域在未来具有潜力的研究方向, 希望可以进一步推动神经网络鲁棒性验证的研究.
| [1] |
Newell A, Simon HA. Human Problem Solving. Englewood Cliffs: Prentice-Hall, 1972.
|
| [2] |
Weizenbaum J. Eliza—A computer program for the study of natural language communication between man and machine. Communi-cations of the ACM, 1966, 9(1): 36-45.
[doi:10.1145/365153.365168] |
| [3] |
Amato F, López A, Peña-Méndez EM, Vaňhara P, Hampl A, Havel J. Artificial neural networks in medical diagnosis. Journal of Applied Biomedicine, 2013, 11(2): 47-58.
[doi:10.2478/v10136-012-0031-x] |
| [4] |
Lipton ZC, Kale DC, Elkan C, Wetzel R. Learning to diagnose with LSTM recurrent neural networks. arXiv:1511.03677, 2017.
|
| [5] |
Hinton G, Deng L, Yu D, Dahl GE, Mohamed AR, Jaitly N, Senior A, Vanhoucke V, Nguyen P, Sainath TN, Kingsbury B. Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups. IEEE Signal Processing Magazine, 2012, 29(6): 82-97.
[doi:10.1109/MSP.2012.2205597] |
| [6] |
Cisse M, Adi Y, Neverova N, Keshet J. Houdini: Fooling deep structured visual and speech recognition models with adversarial examples. In: Proc. of the 31st Int’l Conf. on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017. 6980–6990.
|
| [7] |
Bojarski M, Del Testa D, Dworakowski D, Firner B, Flepp B, Goyal P, Jackel LD, Monfort M, Muller U, Zhang JK, Zhang X, Zhao JK, Zieba K. End to end learning for self-driving cars. arXiv:1604.07316, 2016.
|
| [8] |
Scheiner N, Appenrodt N, Dickmann J, Sick B. Radar-based road user classification and novelty detection with recurrent neural network ensembles. In: Proc. of the 2019 IEEE Intelligent Vehicles Symp. (IV). Paris: IEEE, 2019. 722–729.
|
| [9] |
Mnih V, Kavukcuoglu K, Silver D, Rusu AA, Veness J, Bellemare MG, Graves A, Riedmiller M, Fidjeland AK, Ostrovski G, Petersen S, Beattie C, Sadik A, Antonoglou I, King H, Kumaran D, Wierstra D, Legg S, Hassabis D. Human-level control through deep reinforcement learning. Nature, 2015, 518(7540): 529-533.
[doi:10.1038/nature14236] |
| [10] |
Silver D, Huang A, Maddison CJ, Guez A, Sifre L, Van Den Driessche G, Schrittwieser J, Antonoglou I, Panneershelvam V, Lanctot M, Dieleman S, Grewe D, Nham J, Kalchbrenner N, Sutskever I, Lillicrap T, Leach M, Kavukcuoglu K, Graepel T, Hassabis D. Mastering the game of go with deep neural networks and tree search. Nature, 2016, 529(7587): 484-489.
[doi:10.1038/nature16961] |
| [11] |
Krizhevsky A, Sutskever I, Hinton GE. ImageNet classification with deep convolutional neural networks. In: Proc. of the 25th Int’l Conf. on Neural Information Processing Systems. Lake Tahoe: Curran Associates Inc., 2012. 1097–1105.
|
| [12] |
Wang F, Jiang MQ, Qian C, Yang S, Li C, Zhang HG, Wang XG, Tang XO. Residual attention network for image classification. In: Proc. of the 2017 IEEE Conf. on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017. 6450–6458.
|
| [13] |
Wang QL, Guo WB, Zhang KX, Ororbia AG, Xing XY, Liu X, Giles CL. Adversary resistant deep neural networks with an application to malware detection. In: Proc. of the 23rd ACM SIGKDD Int’l Conf. on Knowledge Discovery and Data Mining. Halifax: ACM, 2017. 1145–1153.
|
| [14] |
Yuan ZL, Lu YQ, Wang ZG, Xue YB. Droid-Sec: Deep learning in android malware detection. ACM SIGCOMM Computer Communication Review, 2014, 44(4): 371-372.
[doi:10.1145/2740070.2631434] |
| [15] |
Seshia SA, Sadigh D, Sastry SS. Toward verified artificial intelligence. Communications of the ACM, 2022, 65(7): 46-55.
[doi:10.1145/3503914] |
| [16] |
Biggio B, Corona I, Maiorca D, Nelson B, Šrndić N, Laskov P, Giacinto G, Roli F. Evasion attacks against machine learning at test time. In: Proc. of the 2013 European Conf. on Machine Learning and Knowledge Discovery in Databases. Prague: Springer, 2013. 387–402.
|
| [17] |
Athalye A, Engstrom L, Ilyas A, Kwok K. Synthesizing robust adversarial examples. In: Proc. of the 35th Int’l Conf. on Machine Learning. Stockholm: PMLR, 2018. 284–293.
|
| [18] |
Carlini N, Wagner D. Towards evaluating the robustness of neural networks. In: Proc. of the 2017 IEEE Symp. on Security and Privacy. San Jose: IEEE, 2017. 39–57.
|
| [19] |
Goodfellow IJ, Shlens J, Szegedy C. Explaining and harnessing adversarial examples. arXiv:1412.6572, 2014.
|
| [20] |
Park DH, Hendricks LA, Akata A, Rohrbach A, Schiele B, Darrell T, Rohrbach M. Attentive explanations: Justifying decisions and pointing to the evidence (extended abstract). arXiv:1711.07373, 2017.
|
| [21] |
Ribeiro MT, Singh S, Guestrin C. “Why should I trust you?”: Explaining the predictions of any classifier. In: Proc. of the 22nd ACM SIGKDD Int’l Conf. on Knowledge Discovery and Data Mining. San Francisco: ACM, 2016. 1135–1144.
|
| [22] |
Pulina L, Tacchella A. An abstraction-refinement approach to verification of artificial neural networks. In: Proc. of the 22nd Int’l Conf. on Computer Aided Verification. Edinburgh: Springer, 2010. 243–257.
|
| [23] |
Gehr T, Mirman M, Drachsler-Cohen D, Tsankov P, Chaudhuri S, Vechev M. AI2: Safety and robustness certification of neural networks with abstract interpretation. In: Proc. of the 2018 IEEE Symp. on Security and Privacy (SP). San Francisco: IEEE, 2018. 3–18.
|
| [24] |
Mirman M, Gehr T, Vechev M. Differentiable abstract interpretation for provably robust neural networks. In: Proc. of the 35th Int’l Conf. on Machine Learning. Stockholm: PMLR, 2018. 3578–3586.
|
| [25] |
Singh G, Gehr T, Mirman M, Püschel M, Vechev M. Fast and effective robustness certification. In: Proc. of the 32nd Int’l Conf. on Neural Information Processing Systems. Montréal: Curran Associates Inc., 2018. 10825–10836.
|
| [26] |
Singh G, Gehr T, Püschel M, Vechev M. Boosting robustness certification of neural networks. In: Proc. of the 2019 Int’l Conf. on Learning Representations. New Orleans, 2019. 1–12.
|
| [27] |
Singh G, Gehr T, Püschel M, Vechev M. An abstract domain for certifying neural networks. Proc. of the ACM on Programming Languages, 2019, 3: 41.
[doi:10.1145/3290354] |
| [28] |
Singh G, Ganvir R, Püschel M, Vechev M. Beyond the single neuron convex barrier for neural network certification. In: Proc. of the 33rd Int’l Conf. on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2019. 15098–15109.
|
| [29] |
Müller C, Serre F, Singh G, Püschel M, Vechev M. Scaling polyhedral neural network verification on GPUs. In: Proc. of the 4th Machine Learning and Systems Conf. San Jose, 2021. 733–746.
|
| [30] |
Wang SQ, Pei KX, Whitehouse J, Yang JF, Jana S. Formal security analysis of neural networks using symbolic intervals. In: Proc. of the 27th USENIX Security Symp. Baltimore: USENIX Association, 2018. 1599–1614.
|
| [31] |
Weng L, Zhang H, Chen HG, Song Z, Hsieh CJ, Daniel L, Boning D, Dhillon I. Towards fast computation of certified robustness for ReLU networks. In: Proc. of the 35th Int’l Conf. on Machine Learning. Stockholm: PMLR, 2018. 5276–5285.
|
| [32] |
Wang SQ, Pei KX, Whitehouse J, Yang JF, Jana S. Efficient formal safety analysis of neural networks. In: Proc. of the 32nd Int’l Conf. on Neural Information Processing Systems. Montréal: Curran Associates Inc., 2018. 6369–6379.
|
| [33] |
Zhang H, Weng TW, Chen PY, Hsieh CJ, Daniel L. Efficient neural network robustness certification with general activation functions. In: Proc. of the 32nd Int’l Conf. on Neural Information Processing Systems. Montréal: Curran Associates Inc., 2018. 4944–4953.
|
| [34] |
Gowal S, Dvijotham K, Stanforth R, Bunel R, Qin CL, Uesato J, Arandjelovic R, Mann T, Kohli P. Scalable verified training for provably robust image classification. In: Proc. of the 2019 IEEE/CVF Int’l Conf. on Computer Vision. Seoul: IEEE, 2019. 4841–4850.
|
| [35] |
Boopathy A, Weng TW, Chen PY, Liu SJ, Daniel L. CNN-cert: An efficient framework for certifying robustness of convolutional neural networks. Proc. of the 2019 AAAI Conf. on Artificial Intelligence, 2019, 33(1): 3240-3247.
[doi:10.1609/aaai.v33i01.33013240] |
| [36] |
Li JL, Liu JC, Yang PF, Chen LQ, Huang XW, Zhang LJ. Analyzing deep neural networks with symbolic propagation: Towards higher precision and faster verification. In: Proc. of the 26th Int’l Static Analysis Symp. Porto: Springer, 2019. 296–319.
|
| [37] |
Zhang H, Chen HG, Xiao CW, Gowal S, Stanforth R, Li B, Boning D, Hsieh CJ. Towards stable and efficient training of verifiably robust neural networks. arXiv:1906.06316, 2019.
|
| [38] |
Lyu ZY, Ko CY, Kong ZF, Wong N, Lin DH, Daniel L. Fastened CROWN: Tightened neural network robustness certificates. Proc. of the AAAI Conf. on Artificial Intelligence, 2020, 34(4): 5037-5044.
[doi:10.1609/aaai.v34i04.5944] |
| [39] |
Huang XW, Kwiatkowska M, Wang S, Wu M. Safety verification of deep neural networks. In: Proc. of the 29th Int’l Conf. on Computer Aided Verification. Heidelberg: Springer, 2017. 3–29.
|
| [40] |
Katz G, Barrett C, Dill DL, Julian K, Kochenderfer MJ. Reluplex: An efficient SMT solver for verifying deep neural networks. In: Proc. of the 29th Int’l Conf. on Computer Aided Verification. Heidelberg: Springer, 2017. 97–117.
|
| [41] |
Ehlers R. Formal verification of piece-wise linear feed-forward neural networks. In: Proc. of the 15th Int’l Symp. on Automated Technology for Verification and Analysis. Pune: Springer, 2017. 269–286.
|
| [42] |
Gopinath D, Katz G, Pasareanu CS, Barrett C. DeepSafe: A data-driven approach for checking adversarial robustness in neural networks. arXiv:1710.00486, 2020.
|
| [43] |
Katz G, Huang DA, Ibeling D, Julian K, Lazarus C, Lim R, Shah P, Thakoor S, Wu HZ, Zeljić A, Dill DL, Kochenderfer MJ, Barrett C. The marabou framework for verification and analysis of deep neural networks. In: Proc. of the 31st Int’l Conf. on Computer Aided Verification. New York: Springer, 2019. 443–452.
|
| [44] |
Tjeng V, Xiao K, Tedrake R. Evaluating robustness of neural networks with mixed integer programming. arXiv:1711.07356, 2019.
|
| [45] |
Dutta S, Jha S, Sankaranarayanan S, Tiwari A. Output range analysis for deep feedforward neural networks. In: Proc. of the 10th Int’l Symp. on NASA Formal Methods. Newport News: Springer, 2018. 121–138.
|
| [46] |
Wong E, Kolter Z. Provable defenses against adversarial examples via the convex outer adversarial polytope. In: Proc. of the 35th Int’l Conf. on Machine Learning. Stockholm: PMLR, 2018. 5286–5295.
|
| [47] |
Müller MN, Makarchuk G, Singh G, Püschel M, Vechev MT. PRIMA: General and precise neural network certification via scalable convex hull approximations. Proc. of the ACM on Programming Languages, 2022, 6: 43.
[doi:10.1145/3498704] |
| [48] |
Anderson G, Pailoor S, Dillig I, Chaudhuri S. Optimization and abstraction: A synergistic approach for analyzing neural network robustness. In: Proc. of the 40th ACM SIGPLAN Conf. on Programming Language Design and Implementation. Phoenix: ACM, 2019. 731–744.
|
| [49] |
Yang PF, Li RJ, Li JL, Huang CC, Wang JY, Sun J, Xue B, Zhang LJ. Improving neural network verification through spurious region guided refinement. In: Proc. of the 27th Int’l Conf. on Tools and Algorithms for the Construction and Analysis of Systems. Luxembourg City: Springer, 2021. 389–408.
|
| [50] |
Ashok P, Hashemi V, Křetínskỳ J, Mohr S. DeepAbstract: Neural network abstraction for accelerating verification. In: Proc. of the 18th Int’l Symp. on Automated Technology for Verification and Analysis. Hanoi: Springer, 2020. 92–107.
|
| [51] |
Elboher YY, Gottschlich J, Katz G. An abstraction-based framework for neural network verification. In: Proc. of the 32nd Int’l Conf. on Computer Aided Verification. Los Angeles: Springer, 2020. 43–65.
|
| [52] |
Hein M, Andriushchenko M. Formal guarantees on the robustness of a classifier against adversarial manipulation. In: Proc. of the 31st Int’l Conf. on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017. 2263–2273.
|
| [53] |
Weng TW, Zhang H, Chen PY, Yi JF, Su D, Gao YP, Hsieh CJ, Daniel L. Evaluating the robustness of neural networks: An extreme value theory approach. arXiv:1801.10578, 2018.
|
| [54] |
Ko CY, Lyu ZY, Weng L, Daniel L, Wong N, Lin DH. POPQORN: Quantifying robustness of recurrent neural networks. In: Proc. of the 36th Int’l Conf. on Machine Learning. Long Beach: PMLR, 2019. 3468–3477.
|
| [55] |
Du TY, Ji SL, Shen LJ, Zhang Y, Li JF, Shi J, Fang CF, Yin JW, Beyah R, Wang T. Cert-RNN: Towards certifying the robustness of recurrent neural networks. In: Proc. of the 2021 ACM SIGSAC Conf. on Computer and Communications Security. ACM, 2021. 516–534.
|
| [56] |
Ryou W, Chen JY, Balunovic M, Singh G, Dan A, Vechev M. Scalable polyhedral verification of recurrent neural networks. In: Proc. of the 33rd Int’l Conf. on Computer Aided Verification. Springer, 2021. 225–248.
|
| [57] |
Akintunde ME, Kevorchian A, Lomuscio A, Pirovano E. Verification of RNN-based neural agent-environment systems. Proc. of the AAAI Conf. on Artificial Intelligence, 2019, 33(1): 6006-6013.
[doi:10.1609/aaai.v33i01.33016006] |
| [58] |
Zhang HC, Shinn M, Gupta A, Gurfinkel A, Le N, Narodytska N. Verification of recurrent neural networks for cognitive tasks via reachability analysis. In: Proc. of the 24th European Conf. on Artificial Intelligence, including the 10th Conf. on Prestigious Applications of Artificial Intelligence. Santiago de Compostela: IOS Press, 2020. 1690–1697.
|
| [59] |
Jacoby Y, Barrett C, Katz G. Verifying recurrent neural networks using invariant inference. In: Proc. of the 18th Int’l Symp. on Automated Technology for Verification and Analysis. Hanoi: Springer, 2020. 57–74.
|
| [60] |
Wang Q, Zhang K, Liu X, Giles CL. Verification of recurrent neural networks through rule extraction. arXiv:1811.06029, 2018.
|
| [61] |
Vengertsev D, Sherman E. Recurrent neural network properties and their verification with Monte Carlo techniques. In: Proc. of the 2020 CEUR Workshop. 2020. 178–185.
|
| [62] |
Mayr F, Yovine S, Visca R. Property checking with interpretable error characterization for recurrent neural networks. Machine Learning and Knowledge Extraction, 2021, 3(1): 205-227.
[doi:10.3390/make3010010] |
| [63] |
Khmelnitsky I, Neider D, Roy R, Xie X, Barbot B, Bollig B, Finkel A, Haddad S, Leucker M, Ye L. Property-directed verification and robustness certification of recurrent neural networks. In: Proc. of the 19th Int’l Symp. on Automated Technology for Verification and Analysis. Gold Coast: Springer, 2021. 364–380.
|
| [64] |
Ruan WJ, Huang XW, Kwiatkowska M. Reachability analysis of deep neural networks with provable guarantees. In: Proc. of the 27th Int’l Joint Conf. on Artificial Intelligence. 2018. 2651–2659.
|
| [65] |
Bunel R, Turkaslan I, Torr PHS, Kohli P, Kumar MP. A unified view of piecewise linear neural network verification. In: Proc. of the 32nd Int’l Conf. on Neural Information Processing Systems. Montréal: Curran Associates Inc., 2018. 4795–4804.
|
| [66] |
Fischetti M, Jo J. Deep neural networks as 0-1 mixed integer linear programs: A feasibility study. arXiv:1712.06174, 2017.
|
| [67] |
Fischetti M, Jo J. Deep neural networks and mixed integer linear optimization. Constraints, 2018, 23(3): 296-309.
[doi:10.1007/s10601-018-9285-6] |
| [68] |
Zhang YD, Zhao Z, Chen GK, Song F, Chen TL. BDD4BNN: A BDD-based quantitative analysis framework for binarized neural networks. In: Proc. of the 33rd Int’l Conf. on Computer Aided Verification. Springer, 2021. 175–200.
|
| [69] |
Dvijotham K, Gowal S, Stanforth R, Arandjelovic R, O’Donoghue B, Uesato J, Kohli P. Training verified learners with learned verifiers. arXiv:1805.10265, 2018.
|
| [70] |
Dvijotham K, Stanforth R, Gowal S, Mann T, Kohli P. A dual approach to scalable verification of deep networks. arXiv:1803.06567, 2018.
|
| [71] |
Raghunathan A, Steinhardt J, Liang P. Certified defenses against adversarial examples. arXiv:1801.09344, 2020.
|
| [72] |
Prabhakar P, Afzal ZR. Abstraction based output range analysis for neural networks. In: Proc. of the 33rd Int’l Conf. on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2019. 15788–15798.
|
| [73] |
Sinha A, Namkoong H, Duchi J. Certifiable distributional robustness with principled adversarial training. arXiv:1710.10571, 2017.
|
| [74] |
Griva I, Nash SG, Sofer A. Linear and Nonlinear Optimization. 2nd ed., Philadelphia: SIAM, 2009.
|
| [75] |
Bastani O, Ioannou Y, Lampropoulos L, Vytiniotis D, Nori AV, Criminisi A. Measuring neural net robustness with constraints. In: Proc. of the 30th Int’l Conf. on Neural Information Processing Systems. Barcelona: Curran Associates Inc., 2016. 2621–2629.
|
| [76] |
Fawzi A, Fawzi O, Frossard P. Analysis of classifiers’ robustness to adversarial perturbations. Machine Learning, 2018, 107(3): 481-508.
[doi:10.1007/s10994-017-5663-3] |
| [77] |
Scheibler K, Winterer L, Wimmer R, Becker B. Towards verification of artificial neural networks. In: Proc. of the 2015 MBMV. Chemnitz, 2015. 30–40.
|
| [78] |
Narodytska N, Kasiviswanathan S, Ryzhyk L, Sagiv M, Walsh T. Verifying properties of binarized deep neural networks. Proc. of the AAAI Conf. on Artificial Intelligence, 2018, 32(1): 6615-6624.
[doi:10.1609/aaai.v32i1.12206] |
| [79] |
Julian KD, Lopez J, Brush JS, Owen MP, Kochenderfer MJ. Policy compression for aircraft collision avoidance systems. In: Proc. of the 35th IEEE/AIAA Digital Avionics Systems Conf. (DASC). Sacramento: IEEE, 2016. 1–10.
|
| [80] |
Kazak Y, Barrett C, Katz G, Schapira M. Verifying deep-RL-driven systems. In: Proc. of the 2019 Workshop on Network Meets AI & ML. Beijing: ACM, 2019. 83–89.
|
| [81] |
Katz G, Barrett C, Dill DL, Julian K, Kochenderfer MJ. Towards proving the adversarial robustness of deep neural networks. Electronic Proc. in Theoretical Computer Science, 2017, 257: 19-26.
[doi:10.4204/EPTCS.257.3] |
| [82] |
Xiang WM, Tran HD, Johnson TT. Output reachable set estimation and verification for multilayer neural networks. IEEE Trans. on Neural Networks and Learning Systems, 2018, 29(11): 5777-5783.
[doi:10.1109/TNNLS.2018.2808470] |
| [83] |
Lomuscio A, Maganti L. An approach to reachability analysis for feed-forward ReLU neural networks. arXiv:1706.07351, 2017.
|
| [84] |
Cheng CH, Nührenberg G, Ruess H. Maximum resilience of artificial neural networks. In: Proc. of the 15th Int’l Symp. on Automated Technology for Verification and Analysis. Pune: Springer, 2017. 251–268.
|
| [85] |
Pulina L, Tacchella A. Checking safety of neural networks with SMT solvers: A comparative evaluation. In: Proc. of the 12th Artificial Intelligence around Man and Beyond Int’l Conf. of the Italian Association for Artificial Intelligence. Palermo: Springer, 2011. 127–138.
|
| [86] |
Pulina L, Tacchella A. Challenging SMT solvers to verify neural networks. AI Communications, 2012, 25(2): 117-135.
[doi:10.3233/AIC-2012-0525] |
| [87] |
Ghorbal K, Goubault E, Putot S. The Zonotope abstract domain Taylor1+. In: Proc. of the 21st Int’l Conf. on Computer Aided Verification. Grenoble: Springer, 2009. 627–633.
|
| [88] |
Mirman M, Singh G, Vechev M. A provable defense for deep residual networks. arXiv:1903.12519, 2020.
|
| [89] |
Srinivas S, Babu RV. Data-free parameter pruning for deep neural networks. In: Proc. of the 2015 British Machine Vision Conf. Swansea: BMVA Press, 2015. 1–12.
|
| [90] |
Zhong GQ, Yao H, Zhou HY. Merging neurons for structure compression of deep networks. In: Proc. of the 24th Int’l Conf. on Pattern Recognition (ICPR). Beijing: IEEE, 2018. 1462–1467.
|
| [91] |
Han S, Mao HZ, Dally WJ. Deep compression: Compressing deep neural network with pruning, trained quantization and huffman coding. arXiv:1510.00149, 2015.
|
| [92] |
Jin P, Tian JX, Zhi DP, Wen XJ, Zhang M. TRAINIFY: A CEGAR-driven training and verification framework for safe deep reinforcement learning. In: Proc. of the 34th Int’l Conf. on Computer Aided Verification. Haifa: Springer, 2022. 193–218.
|
| [93] |
Gowal S, Dvijotham K, Stanforth R, Bunel R, Qin CL, Uesato J, Arandjelovic R, Mann T, Kohli P. On the effectiveness of interval bound propagation for training verifiably robust models. arXiv:1810.12715, 2019.
|
| [94] |
Wong E, Schmidt FR, Metzen JH, Kolter JZ. Scaling provable adversarial defenses. In: Proc. of the 32nd Int’l Conf. on Neural Information Processing Systems. Montréal: Curran Associates Inc., 2018. 8410–8419.
|
| [95] |
Salman H, Yang G, Zhang H, Hsieh CJ, Zhang PC. A convex relaxation barrier to tight robustness verification of neural networks. In: Proc. of the 33rd Int’l Conf. on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2019. 9835–9846.
|
| [96] |
Yang PF, Li JL, Liu JC, Huang CC, Li RJ, Chen LQ, Huang XW, Zhang LJ. Enhancing robustness verification for deep neural networks via symbolic propagation. Formal Aspects of Computing, 2021, 33(3): 407-435.
[doi:10.1007/s00165-021-00548-1] |
| [97] |
Li RJ, Li JL, Huang CC, Yang PF, Huang XW, Zhang LJ, Xue B, Hermanns H. PRODeep: A platform for robustness verification of deep neural networks. In: Proc. of the 28th ACM Joint Meeting on European Software Engineering Conf. and Symp. on the Foundations of Software Engineering. Virtual Event: ACM, 2020. 1630–1634.
|
| [98] |
Szegedy C, Zaremba W, Sutskever I, Bruna J, Erhan D, Goodfellow IJ, Fergus R. Intriguing properties of neural networks. arXiv:1312.6199, 2013.
|
| [99] |
Hull J, Ward D, Zakrzewski RR. Verification and validation of neural networks for safety-critical applications. In: Proc. of the 2002 American Control Conf. (IEEE Cat. No. CH37301). Anchorage: IEEE, 2002. 4789–4794.
|
| [100] |
Weng TW, Zhang H, Chen PY, Lozano A, Hsieh CJ, Daniel L. On extensions of clever: A neural network robustness evaluation algorithm. In: Proc. of the 2018 IEEE Global Conf. on Signal and Information Processing (GlobalSIP). Anaheim: IEEE, 2018. 1159–1163.
|
| [101] |
Athalye A, Carlini N, Wagner D. Obfuscated gradients give a false sense of security: Circumventing defenses to adversarial examples. In: Proc. of the 35th Int’l Conf. on Machine Learning. Stockholm: PMLR, 2018. 274–283.
|
| [102] |
Papernot N, McDaniel P, Goodfellow I, Jha S, Celik ZB, Swami A. Practical black-box attacks against machine learning. In: Proc. of the 2017 ACM on Asia Conf. on Computer and Communications Security. Abu Dhabi: ACM, 2017. 506–519.
|
| [103] |
Papernot N, McDaniel P, Wu X, Jha S, Swami A. Distillation as a defense to adversarial perturbations against deep neural networks. In: Proc. of the 2016 IEEE Symp. on Security and Privacy (SP). San Jose: IEEE, 2016. 582–597.
|
| [104] |
Raghunathan A, Steinhardt J, Liang PS. Semidefinite relaxations for certifying robustness to adversarial examples. In: Proc. of the 32nd Int’l Conf. on Neural Information Processing Systems. Montréal: Curran Associates Inc., 2018. 10900–10910.
|
| [105] |
Liu CL, Arnon T, Lazarus C, Strong C, Barrett C, Kochenderfer MJ. Algorithms for verifying deep neural networks. Foundations and Trends® in Optimization, 2021, 4(3–4): 244–404.
|
| [106] |
Huang XW, Kroening D, Ruan WJ, Sharp J, Sun YC, Thamo E, Wu M, Yi XP. A survey of safety and trustworthiness of deep neural networks: Verification, testing, adversarial attack and defence, and interpretability. Computer Science Review, 2020, 37: 100270.
[doi:10.1016/j.cosrev.2020.100270] |
| [107] |
Ji SL, Du TY, Deng SG, Cheng P, Shi J, Yang M, Li B. Robustness certification research on deep learning models: A survey. Chinese Journal of Computers, 2022, 45(1): 190-206(in Chinese with English abstract).
[doi:10.11897/SP.J.1016.2022.00190] |
| [108] |
Vanilla recurrent neural network. 2021. http://calvinfeng.gitbook.io/machine-learning-notebook/supervised-learning/recurrent-neural-network/recurrent_neural_networks
|
| [109] |
Hochreiter S, Schmidhuber J. Long short-term memory. Neural Computation, 1997, 9(8): 1735-1780.
[doi:10.1162/neco.1997.9.8.1735] |
| [110] |
Cho K, van Merrienboer B, Gülçehre Ç, Bahdanau D, Bougares F, Schwenk H, Bengio Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. In: Proc. of the 2014 Conf. on Empirical Methods in Natural Language Processing. Doha: ACL, 2014. 1724–1734.
|
| [111] |
Wang SH, Jiang J. Learning natural language inference with LSTM. In: Proc. of the 2016 Conf. of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies. San Diego: Association for Computational Linguistics, 2016. 1442–1451.
|
| [112] |
Wang YQ, Huang ML, Zhu XY, Zhao L. Attention-based LSTM for aspect-level sentiment classification. In: Proc. of the 2016 Conf. on Empirical Methods in Natural Language Processing. Austin: Association for Computational Linguistics, 2016. 606–615.
|
| [113] |
Wang SH, Jiang J. Machine comprehension using match-LSTM and answer pointer. arXiv:1608.07905, 2017.
|
| [114] |
Hermann KM, Kočiský T, Grefenstette E, Espeholt L, Kay W, Suleyman M, Blunsom P. Teaching machines to read and comprehend. In: Proc. of the 28th Int’l Conf. on Neural Information Processing Systems. Montreal: MIT Press, 2015. 1693–1701.
|
| [115] |
Xu AB, Liu Z, Guo YF, Sinha V, Akkiraju R. A new chatbot for customer service on social media. In: Proc. of the 2017 CHI Conf. on Human Factors in Computing Systems. Denver: ACM, 2017. 3506–3510.
|
| [116] |
Olah Christopher. Understanding LSTM networks. 2015. http://colah.github.io/posts/2015-08-Understanding-LSTMs/
|
| [117] |
Wang QL, Zhang KX, Liu X, Giles CL. Verification of recurrent neural networks through rule extraction. arXiv:1811.06029, 2018.
|
| [118] |
Cousot P, Cousot R. Abstract interpretation: A unified lattice model for static analysis of programs by construction or approximation of fixpoints. In: Proc. of the 4th ACM SIGACT-SIGPLAN Symp. on Principles of Programming Languages. Los Angeles: ACM, 1977. 238–252.
|
| [119] |
Papernot N, McDaniel P, Swami A, Harang R. Crafting adversarial input sequences for recurrent neural networks. In: Proc. of the 2016 IEEE Military Communications Conf. Baltimore: IEEE, 2016. 49–54.
|
| [120] |
Cheng MH, Yi JF, Chen PY, Zhang H, Hsieh CJ. Seq2sick: Evaluating the robustness of sequence-to-sequence models with adversarial examples. Proc. of the AAAI Conf. on Artificial Intelligence, 2020, 34(4): 3601-3608.
[doi:10.1609/aaai.v34i04.5767] |
| [121] |
Akintunde ME, Lomuscio A, Maganti L, Pirovano E. Reachability analysis for neural agent-environment systems. In: Proc. of the 16th Int’l Conf. on Principles of Knowledge Representation and Reasoning, 2018. 184–193.
|
| [122] |
Tran HD, Yang XD, Lopez DM, Musau P, Nguyen LV, Xiang WM, Bak S, Johnson TT. NNV: The neural network verification tool for deep neural networks and learning-enabled cyber-physical systems. In: Proc. of the 32nd Int’l Conf. on Computer Aided Verification. Los Angeles: Springer, 2020. 3–17.
|
| [123] |
Hopcroft JE, Motwani R, Ullman JD. Introduction to automata theory, languages, and computation, 2nd edition. ACM SIGACT News, 2001, 32(1): 60-65.
[doi:10.1145/568438.568455] |
| [124] |
Sakarovitch J. Elements of Automata Theory. Cambridge: Cambridge University Press, 2009.
|
| [125] |
Clarke EM. Model checking. In: Proc. of the 17th Conf. on Foundations of Software Technology and Theoretical Computer Science. Kharagpur: Springer, 1997. 54–56.
|
| [126] |
Weiss G, Goldberg Y, Yahav E. Extracting automata from recurrent neural networks using queries and counterexamples. In: Proc. of the 35th Int’l Conf. on Machine Learning. Stockholm: PMLR, 2018. 5247–5256.
|
| [127] |
Zhang XY, Du XN, Xie XF, Ma L, Liu Y, Sun M. Decision-guided weighted automata extraction from recurrent neural networks. Proc. of the AAAI Conf. on Artificial Intelligence, 2021, 35(13): 11699–11707.
|
| [128] |
Ayache S, Eyraud R, Goudian N. Explaining black boxes on sequential data using weighted automata. In: Proc. of the 14th Int’l Conf. on Grammatical Inference. Wrocław: PMLR, 2019. 81–103.
|
| [129] |
Okudono T, Waga M, Sekiyama T, Hasuo I. Weighted automata extraction from recurrent neural networks via regression on state spaces. Proc. of the AAAI Conf. on Artificial Intelligence, 2020, 34(4): 5306-5314.
[doi:10.1609/aaai.v34i04.5977] |
| [130] |
Jacobsson H. Rule extraction from recurrent neural networks: Ataxonomy and review. Neural Computation, 2005, 17(6): 1223-1263.
[doi:10.1162/0899766053630350] |
| [131] |
Wang QL, Zhang KX, Ororbia AG II, Xing XY, Liu X, Giles CL. An empirical evaluation of rule extraction from recurrent neural networks. Neural Computation, 2018, 30(9): 2568-2591.
[doi:10.1162/neco_a_01111] |
| [132] |
Giles CL, Miller CB, Chen D, Chen HH, Sun GZ, Lee YC. Learning and extracting finite state automata with second-order recurrent neural networks. Neural Computation, 1992, 4(3): 393-405.
[doi:10.1162/neco.1992.4.3.393] |
| [133] |
Giles CL, Sun GZ, Chen HH, Lee YC, Chen D. Higher order recurrent networks and grammatical inference. In: Advances in Neural Information Processing Systems 2. San Francisco: Morgan Kaufmann Publishers Inc., 1989. 380–387.
|
| [134] |
Tretmans J. Conformance testing with labelled transition systems: Implementation relations and test generation. Computer Networks and ISDN Systems, 1996, 29(1): 49-79.
[doi:10.1016/S0169-7552(96)00017-7] |
| [135] |
Mayr F, Yovine S. Regular inference on artificial neural networks. In: Proc. of the 2018 Int’l Cross-domain Conf. for Machine Learning and Knowledge Extraction. Hamburg: Springer, 2018. 350–369.
|
| [136] |
Clarke E, Grumberg O, Jha S, Lu Y, Veith H. Counterexample-guided abstraction refinement. In: Proc. of the 12th Int’l Conf. on Computer Aided Verification. Chicago: Springer, 2000. 154–169.
|
| [137] |
Bacciu D, Carta A, Di Sarli D, Gallicchio C, Lomonaco V, Petroni S. Towards functional safety compliance of recurrent neural networks. In: Proc. of the 1st Int’l Conf. on AI for People: Towards Sustainable AI, CAIP 2021. Bologna: European Alliance for Innovation, 2021. 1–10.
|
| [138] |
Mohammadinejad S, Paulsen B, Deshmukh JV, et al. DiffRNN: Differential verification of recurrent neural networks. In: Proc. of the 19th Int’l Conf. on Formal Modeling and Analysis of Timed Systems. Paris: Springer, 2021. 117–134.
|
| [139] |
Zhang YH, Albarghouthi A, D’Antoni L. Certified robustness to programmable transformations in LSTMs. In: Proc. of the 2021 Conf. on Empirical Methods in Natural Language Processing. Punta Cana: Association for Computational Linguistics, 2021. 1068–1083.
|
| [140] |
Dong XS, Luu AT, Ji RR, Liu H. Towards robustness against natural language word substitutions. arXiv:2107.13541, 2021.
|
| [141] |
Xu KD, Shi ZX, Zhang H, Wang YH, Chang KW, Huang ML, Kailkhura B, Lin X, Hsieh CJ. Automatic perturbation analysis for scalable certified robustness and beyond. In: Proc. of the 34th Int’l Conf. on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2020. 1129–1141.
|
| [142] |
Shi ZX, Zhang H, Chang KW, Huang ML, Hsieh CJ. Robustness verification for Transformers. arXiv: 2002.06622, 2020.
|
| [143] |
Zhang WE, Sheng QZ, Alhazmi A, Li CL. Adversarial attacks on deep-learning models in natural language processing: A survey. ACM Trans. on Intelligent Systems and Technology, 2020, 11(3): 24.
[doi:10.1145/3374217] |
| [144] |
Zheng HB, Chen JY, Zhang Y, Zhang XH, Ge CP, Liu Z, Ouyang YK, Ji SL. Survey of adversarial attack, defense and robustness analysis for natural language processing. Journal of Computer Research and Development, 2021, 58(8): 1727-1750(in Chinese with English abstract).
[doi:10.7544/issn1000-1239.2021.20210304] |
| [145] |
Leino K, Wang ZF, Fredrikson M. Globally-robust neural networks. In: Proc. of the 38th Int’l Conf. on Machine Learning. PMLR, 2021. 6212–6222.
|
| [146] |
Ruan WJ, Wu M, Sun YC, Huang XW, Kroening D, Kwiatkowska M. Global robustness evaluation of deep neural networks with provable guarantees for the hamming distance. In: Proc. of the 28th Int’l Joint Conf. on Artificial Intelligence. Macao: IJCAI, 2019. 5944–5952.
|
| [147] |
Sun WD, Lu YT, Zhang XY, Sun M. DeepGlobal: A framework for global robustness verification of feedforward neural networks. Journal of Systems Architecture, 2022, 128: 102582.
[doi:10.1016/j.sysarc.2022.102582] |
| [148] |
Kalra N, Paddock SM. Driving to safety: How many miles of driving would it take to demonstrate autonomous vehicle reliability?. Transportation Research Part A: Policy and Practice, 2016, 94: 182-193.
[doi:10.1016/j.tra.2016.09.010] |
| [149] |
Baluta T, Chua ZL, Meel KS, Saxena P. Scalable quantitative verification for deep neural networks. In: Proc. of the 43rd IEEE/ACM Int’l Conf. on Software Engineering (ICSE). Madrid: IEEE, 2021. 312–323.
|
| [150] |
Li RJ, Yang PF, Huang CC, Sun YC, Xue B, Zhang LJ. Towards practical robustness analysis for DNNs based on PAC-model learning. In: Proc. of the 44th Int’l Conf. on Software Engineering. Pittsburgh: ACM, 2022. 2189–2201.
|
| [151] |
Mangal R, Nori AV, Orso A. Robustness of neural networks: A probabilistic and practical approach. In: Proc. of the 41st Int’l Conf. on Software Engineering: New Ideas and Emerging Results. Montreal: IEEE, 2019. 93–96.
|
| [152] |
Webb S, Rainforth T, the YW, Kumar MP. A statistical approach to assessing neural network robustness. arXiv:1811.07209, 2019.
|
| [153] |
Balunović M, Baader M, Singh G, Gehr T, Vechev M. Certifying geometric robustness of neural networks. In: Proc. of the 33rd Int’l Conf. on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2019. 15313–15323.
|
| [154] |
Cardelli L, Kwiatkowska M, Laurenti L, Patane A. Robustness guarantees for Bayesian inference with Gaussian processes. Proc. of the AAAI Conf. on Artificial Intelligence, 2019, 33(1): 7759-7768.
[doi:10.1609/aaai.v33i01.33017759] |
| [155] |
Miller T. Explanation in artificial intelligence: Insights from the social sciences. Artificial Intelligence. Artificial Intelligence, 2019, 267: 1-38.
[doi:10.1016/j.artint.2018.07.007] |
| [156] |
Biran O, Cotton C. Explanation and justification in machine learning: A survey. In: Proc. of the 2017 IJCAI Workshop on Explainable AI (XAI). 2017. 8–13.
|
| [157] |
Ahmad MA, Eckert C, Teredesai A. Interpretable machine learning in healthcare. In: Proc. of the 2018 ACM Int’l Conf. on Bioinformatics, Computational Biology, and Health Informatics. Washington: ACM, 2018. 559–560.
|
| [158] |
Liu WW, Song F, Zhang THR, Wang J. Verifying ReLU neural networks from a model checking perspective. Journal of Computer Science and Technology, 2020, 35(6): 1365-1381.
[doi:10.1007/s11390-020-0546-7] |
| [159] |
Guo XW, Wan WJ, Zhang ZD, Zhang M, Song F, Wen XJ. Eager falsification for accelerating robustness verification of deep neural networks. In: Proc. of the 32nd IEEE Int’l Symp. on Software Reliability Engineering. Wuhan: IEEE, 2021. 345–356.
|
| [160] |
Zhang ZD, Liu J, Liu GJ, Wang JC, Zhang J. Robustness verification of swish neural networks embedded in autonomous driving systems. IEEE Trans. on Computational Social Systems, 2022. 1–10.
|
| [161] |
Zhang YD, Zhao Z, Chen GK, Song F, Zhang M, Chen TL, Sun J. QVIP: An ILP-based formal verification approach for quantized neural networks. In: Proc. of the 37th IEEE/ACM Int’l Conf. on Automated Software Engineering. Rochester: ACM, 2022. 82.
|
| [162] |
Dreossi T, Fremont DJ, Ghosh S, Kim E, Ravanbakhsh H, Vazquez-Chanlatte M, Seshia SA. VerifAI: A toolkit for the formal design and analysis of artificial intelligence-based systems. In: Proc. of the 31st Int’l Conf. on Computer Aided Verification. New York City: Springer, 2019. 432–442.
|
| [163] |
Dreossi T, Donzé A, Seshia SA. Compositional falsification of cyber-physical systems with machine learning components. Journal of Automated Reasoning, 2019, 63(4): 1031-1053.
[doi:10.1007/s10817-018-09509-5] |
| [164] |
Zhou ZY, Liu GJ. RoMFAC: A robust mean-field actor-critic reinforcement learning against adversarial perturbations on states. arXiv: 2205.07229, 2022.
|
| [165] |
Balakrishnan A, Deshmukh J, Hoxha B, Yamaguchi T, Fainekos G. PerceMon: Online monitoring for perception systems. In: Proc. of the 21st Int’l Conf. on Runtime Verification. Virtual Event: Springer, 2021. 297–308.
|
| [107] |
纪守领, 杜天宇, 邓水光, 程鹏, 时杰, 杨珉, 李博. 深度学习模型鲁棒性研究综述. 计算机学报, 2022, 45(1): 190-206.
[doi:10.11897/SP.J.1016.2022.00190] |
| [144] |
郑海斌, 陈晋音, 章燕, 张旭鸿, 葛春鹏, 刘哲, 欧阳亦可, 纪守领. 面向自然语言处理的对抗攻防与鲁棒性分析综述. 计算机研究与发展, 2021, 58(8): 1727-1750.
[doi:10.7544/issn1000-1239.2021.20210304] |