基于区域划分与降维的高维学习型索引
张少敏
,
蔡盼
,
李翠平
,
陈红
软件学报  2023, Vol. 34 2023, Vol. 34 Issue (5): 2413-2426 Issue (5): 2413-2426 |
随着互联网和大数据时代的发展, 各种数据爆炸式增长, 数据格式也随之越来越复杂, 基础数据类型以外的如图像、声音、文本等复杂数据类型的使用也越来越广泛, 这些数据大多是以高维度的形式进行存储、运算, 这就使得快速准确的高维数据查询变得更加重要, 如何构建高效快速且节省内存空间的高维索引成为提高数据查询效率的关键.
常用的高维数据查询类型有范围查询、点查询和最近邻查询等. 范围查询即在给定数据空间中, 返回一定查询范围内的所有数据点; 点查询可以看做一种特殊的范围查询, 即给定的查询范围很小, 只有唯一满足条件的数据点; 最近邻查询是给定数据空间中的一个目标点, 返回空间中距离它最近的一个或几个数据点.
由于大数据应用中数据量的庞大, 使得用遍历的方式对高维数据进行查询变得低效不可行, 所以必须为高维数据搭建专门的索引结构. 最典型的传统高维索引结构有R树[1]及其各种变体如R* 树[2]、R+ 树[3]、QR树[4]等, 以及四叉树及其各种变体[5-7]. R树是B树在高维数据的拓展, 也是一种平衡树. 它将高维数据按范围划分, 每个结点都对应一个区域, 非叶结点中存储其所有子结点的区域范围, 保证它的所有子结点区域都落在它的区域范围之内; 叶结点中存储其区域范围之内的所有高维对象的外接矩形. 每个结点所能拥有的子结点数目有上、下限, 用来保证R树的动态平衡. R树极大地提高了高维数据的检索效率, 但是它本身存在一定的缺陷, 其各种变体尝试从不同方面弥补它的不足, 但是当数据维度较大的时候, 它们的查询速度会骤降, 数据量增加时, 也会影响它们的查询效率, 而且R树本身内存占用极大, 构建过程也十分耗时. 四叉树与R树类似, 它是将平面空间四等分, 然后在四等分上迭代划分, 它的应用只局限于二维空间, 而且查询与维护的开销较大. 在数据高度发达的当下, 显然传统高维索引并不能满足人们的查询需求. 为了解决传统高维索引结构的缺点, 国内外研究者在索引结构中引入了机器学习和深度学习的知识, 利用学习的方式来代替传统索引, 将查询转换为模型的一次预测, 这样就可以依赖计算机的计算优势来提高索引查询效率. 最初的高维学习型索引是对整个数据空间进行模型训练, 但是结果并不理想, 模型难以收敛, 精度明显无法满足需求, 而且模型只能针对单一的数据分布, 迁移性很差, 于是数据降维和空间区域划分等策略被运用到了索引结构中. 为了有效地使用学习型方法, 首先需要将高维数据按照一定的顺序排列, 数据降维类索引的思路是先将空间中所有点降至一维, 然后在一维有序数据上训练模型, 这类方法会将全部降维后的数据进行排序, 并对整体数据训练模型, 所以会存在误差大、模型复杂、训练时间久、难以收敛等缺点; 空间区域划分类索引首先在数据轴上对空间进行切分, 然后对数据空间进行排序, 从而使空间内的数据有序, 再利用学习的方式筛选与查询相关的区域, 遍历相关区域内数据点. 这种方法稳定性较差, 查询效率易受查询范围影响.
针对上述问题, 本文尝试结合空间区域划分和数据降维两种策略, 尽可能将数据分布的信息全部利用起来, 构造符合数据分布的高维学习型索引结构, 提升高维数据查询效率. 除此之外利用最简单的多段线性模型, 在保证查询精确度的前提下, 尽可能降低索引的构建开销和存储开销.
1 相关工作近年, 机器学习和深度学习技术与数据库系统的结合越来越紧密, 如文献[1]介绍, 数据库的查询优化、数据布局、索引构建、索引推荐等方面都引入了学习型的思路, 而机器学习和深度学习也常常会依靠数据库技术来提速. 数据库系统与机器学习已经发展到了互相促进、互相提升的阶段. 索引技术也是数据库与机器学习结合的重要研究方向. 与传统的数据库索引相比, 学习型索引有更好的搜索性能和更低的空间占用率. 传统索引大多是通用数据结构, 并不会考虑底层数据分布, 这就会使得大部分有关数据分布的有效信息被遗漏, 而学习型索引就是将这些信息利用起来, 依据数据分布来构建索引结构, 从而提高检索效率, 它的核心思想是: 将索引看做是一种数据检索的模型.
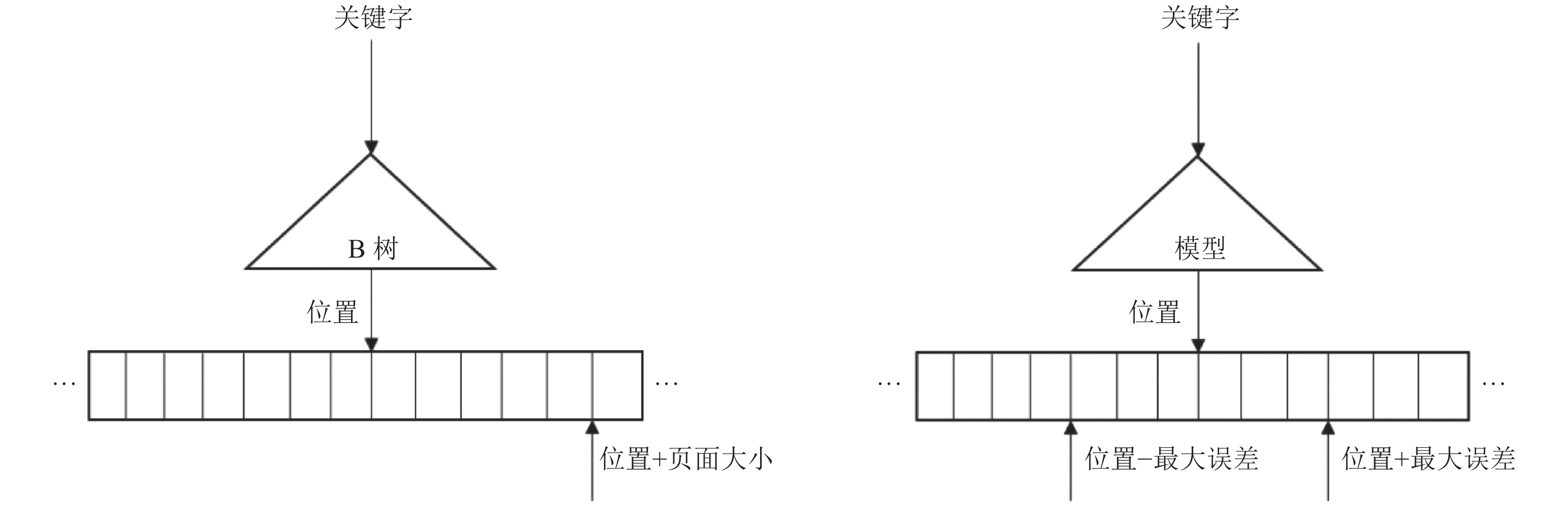
1.1 一维学习型索引学习型索引最早是在2018年由Kraska等人[8]提出. 这篇论文的主要贡献是提出了用模型代替索引结构的思想. 他们认为当数据分布本身存在一定规律的时候, 就可以利用已有的规律进行检索, 而不用通用数据结构. 如有序数据, 可以用近似累计分布函数CDF来预测数据的位置, 累积分布函数模型的预测复杂度为O(n). 如图1所示, 学习型索引将索引结构看作模型, 将传统树型结构的页面大小看做是机器学习模型的最大误差, 只要使得模型的预测误差小于页面大小就等于保证了查询精度. 文献[8]针对这种思路实现了一种递归索引结构, 来解决单个模型在较大数据集上误差太大的问题, 递归结构用多层全连接的模型做索引, 查询的关键字作为输入, 数据位置作为输出, 由上层模型来对下层模型做出选择, 逐层递归, 由最底层模型做出最终预测. 递归索引在每层使用了不同的模型, 顶层因为需要学习大范围的复杂数据分布, 所以使用较为复杂的神经网络, 下层只需要学习少量数据的分布信息, 所以使用简单的线性回归模型来降低模型复杂度, 使得时间和空间的开销都相对更小一些. 而且系统会设置阈值, 当数据分布难以拟合时, 就会在模型最底层使用传统的B树. 在真实数据集的实验中, 递归索引的查询效率和存储空间占用都比传统树形结构索引有了不止一个数量级的提升. 随着学习型索引思路的普及, 众多学习型索引结构也纷纷被提出, 它们分别适用于不同应用场景. 如自适应树[9], 它只对数据进行一次遍历, 然后根据设定的最大误差构建多段模型, 并用树形结构来存放训练结果, 极大地降低了学习型索引的训练时间, 以及模型的空间消耗. 文献[10]是针对动态数据进行构建, 文章认为索引更新的时候, 需要进行大量的数据移动, 于是它改变了原始数据的数据分布, 对原数据进行模型预测, 将数据按照预测的位置存放, 并在数据之间增加大量空隙, 以此来减少索引更新时数据移动带来的开销, 解决了学习型索引不能进行增删改的问题; 文献[11]是在递归模型的基础上更换了底层模型, 用简单的线性模型代替神经网络, 用来降低索引的复杂度; 文献[12]也是根据数据分布学习多个线性模型来进行检索, 并对每个模型的精度进行判断, 当数据不满足线性关系的时候, 更换模型进行拟合; 文献[13]认为递归模型直接用模型对数据进行划分会造成额外的误差, 所以提出使用数据之间的距离作为划分依据, 当相邻数据之间的距离大于阈值之后, 就会进行切分, 然后对每个数据段分别训练模型, 以此来提高模型的精度. 学习型索引的思路不光被应用在数值型索引上, 在其他数据类型上也有诸多成果, 如文献[14]将学习型索引的思路应用到了字符型数据中, 它用字符串中去掉公共前缀的子串来代表整个字符串作为模型的关键字, 并保持原始的字符串排放顺序作为位置, 针对它们训练递归模型; 文献[15]提出用学习型的思路改进布隆过滤器, 提高存在型查询的效率; 文献[16]用线性函数代替插值排序算法, 可以提高排序后查询的速度. 这些研究在不同方面提升了学习型的性能, 使得学习型索引这一研究方向被进一步挖掘. 除了上述种类学习型以外, 还有一些研究是在传统索引结构的基础上进行的, 如文献[17-19]提出的各种索引结构, 它们均以B树为基础, 在其中运用机器学习的方法, 来提高检索速度、更新速度等.
|
图 1 B树与学习型索引 |
随着一维数据上学习型索引的探索, 研究者逐渐把学习的思路代入了多维空间, 用来提升高维索引的性能. 最有代表性的传统多维索引是R树, 但是它本身存在维度爆炸等缺点, 众多研究者试图引入学习型索引的方法来解决传统索引的问题. 高维数据的学习型索引大致可以分为两类: 基于降维的索引和基于空间区域划分的索引.
基于降维的高维学习型索引核心思想是: 先将高维数据降至一维, 然后针对一维有序数据利用现有技术进行检索. 具有代表性的如Wang等人提出的ZM索引[20], 它采用了Z排序方式对高维数据进行预处理. Z排序所依据的Z曲线是一种空间填充曲线, 它可以将多维向量空间完全填充, 使所有的数据点都映射到一维空间, 每个多维向量都可以转换成一个唯一的整数, 即Z地址. 而且可以保证高维数据之间原有的大小关系, 即当一个数据点的每个维度都大于另一个数据点时, 它对应的Z地址也一定大于另一个点. 这就可以保证将高维的范围查询转换成一维数据范围查询. 进行降维后ZM索引将一维数据进行排序, 并选择采用文献[8]先前提出的递归模型, 训练有序一维数据的累积分布函数. 在利用索引进行查询的时候, 首先将查询范围进行降维, 然后利用训练好的递归模型进行预测, 返回全部范围内数据的一维形式, 最后对一维数据进行反映射, 即为满足查询条件的数据点. 在高维数据的降维上, 文献[21]提出了另一种方法. 他们设计的空间索引首先将数据空间根据空间中心点和空间边界进行分区, 并将每个分区边界的中心点定义为该分区的参考点. 然后将数据按照其与所在分区参考点之间的距离进行排序, 从而达到高维数据降维的目的. 文献[22]也提出了不同的索引方式, 他们设计实现的索引结构, 首先根据数据分布, 把数据划分开, 然后选择每个集合的中心作为参考点, 运用与文献[21]一样的方式, 将每个集合内的高维数据转换成与参考点之间的距离, 接着又对集合进行排序, 给每个集合设置一个偏移值, 将全部高维数据转换成距离与偏移的和, 从而实现整体数据的降维. 针对已经降成一维的数据, 文献[22]还是沿用了递归模型的思路, 训练数据的累积分布函数来做检索.
基于空间区域划分的高维学习型索引核心思想是: 根据数据分布对数据空间在数据轴上进行规则的划分, 然后对与查询范围相关的区域进行检索. 具有代表性的成果如文献[8]设计实现的空间索引系统Flood[23]. 系统首先选择查询最频繁的维度进行排序, 然后将剩余维度根据每个维度的数据密度将其划分成小网格. 当使用索引进行查询的时候, 首先通过查询条件得到需要遍历的数据网格, 将索引范围约束在这些网格中, 然后对已经排序的网格进行查找. 由于每个网格内的数据已经根据第一维度排序, 所以可以使用一维索引的技术进行检索. 与文献[23]一样使用空间区域划分方法的还有Li等人设计实现的空间数据索引系统LISA[24]. 它也是根据数据轴对空间进行规则的切分, 然后用学习的方法进行检索. 但是与文献[23]不同的是, 它训练了一个单独的分区预测模型, 学习数据的分区信息, 这样就可以实现对不同数据分布都通用的索引结构. 针对最近邻查询, 文献[25]也提出了一种以学习型方法进行空间划分的方法, 他们根据数据的分布将空间分成尽量均匀的几部分, 保证每个点的最近邻点基本来自相同部分, 这样就可以极大地提高最近邻查询的速度.
除了上述研究成果, 还有许多高维学习型索引结构被提出, 如文献[26]在Flood的基础上, 增加了对倾斜查询和工作负载的考虑, 对网格划分进行了优化, 提高了索引的内存利用率; 文献[27]认为维度爆炸是影响高维索引的主要因素, 于是提出学习各个维度之间的相关性, 对索引中相关性强的维度进行删减, 由此来提高索引的查询效率; 文献[28]将学习型索引运用到地图查询上. 它们大多只可以实现高维空间的某一种查询方式, 并不能同时满足多种查询, 而且也只针对静态数据, 难以实现数据的更新.
2 索引设计本节将详细描述基于空间划分和降维的增强高维学习型索引IHDL (improved high-dimension learned index)的结构设计. 如上文所述, 本文的目标是尽可能利用高维数据的数据分布信息, 构建高效的学习型索引; 同时尽可能降低索引构建和存储的开销, 实现轻量级高维索引. 由于数据本身分布存在差异, 所以将全部数据进行降维排序处理或者是对数据轴进行均匀划分, 并不能有效地将数据分布的信息利用起来, 而且只靠单个机器学习模型很难学习空间数据的整体分布规律, 模型的误差较大. 所以如何根据数据分布将空间分区域处理, 并在每个区域内训练高效的模型结构成了提升高维学习型索引效率的关键.
IHDL索引设计了3个处理阶段对数据分布进行学习: (1)利用聚类算法根据数据的聚集程度将空间划分成K个区域, 使相同区域内的数据分布尽可能集中, 不同区域之间的数据分布尽可能分散, 这样有利于下一步的模型训练; (2)对每个空间区域中的数据, 利用Hilbert编码的方式分别进行降维排序处理, Hilbert编码是现有降维技术中稳定性最好的, 可以在保证空间数据相对位置的前提下实现降维, 而且当数据空间改变, 编码阶数增大的时候, 也可以保证数据点之间的相对位置不被改变; (3)针对每个区域已经降维的数据进行学习型模型的训练, 尽可能去拟合对应空间区域的数据分布. 除此之外, 由于不同数据区域的模型都是独立训练维护, 所以有数据更新需要进行模型重新训练的时候, 只需要对数据更新涉及区域重新训练模型即可, 不需要对整个索引结构进行更改, 从而极大地减少了索引维护的成本, 提高了索引的可扩展性.
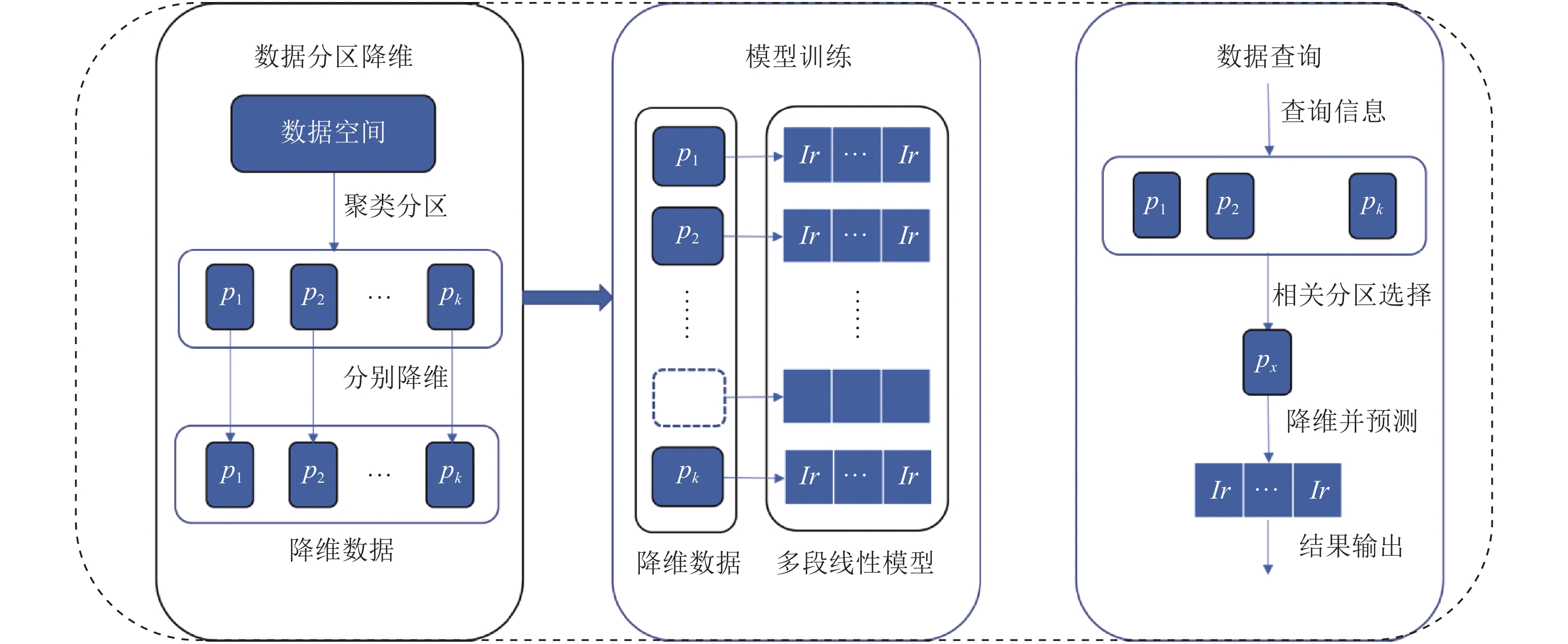
由图2可以看出IHDL索引主要分为3个部分: (1)根据聚类结果对数据空间根据数据的分布情况进行划分, 将整个空间划分成K个部分, 并对每个部分分别进行Hilbert降维处理, 对降维数据进行排序得到K个有序数列; (2)初始化K个模型, 针对K个有序数列进行模型训练, 得到K个一维的学习型索引; (3)进行数据查询时, 首先根据其在空间中的位置, 定位所涉及查询的目标区域, 并对查询边界其进行降维, 然后利用该区域的模型预测数据所在的位置, 根据设定的误差边界在预测位置的两侧进行二分查找. 接下来, 我们将对索引的各个部分进行逐一介绍.
|
图 2 IHDL索引整体架构 |
如上文所述, IHDL索引尽可能根据数据分布进行学习, 从而提高索引的效率, 减少查询误差. 然而空间数据分布普遍较为复杂, 很难用一个模型学习到全部数据分布的信息, 所以需要对数据空间进行有效地分割. 大多空间数据存在一定的聚集性, 如在地图类型数据集中, 整体数据点的分布存在区域性, 反映在现实地图中, 就可以理解为, 有的区域内地点与建筑分布较为密集, 而有的区域则比较稀疏. 所以根据数据分布的聚集情况进行空间划分, 可以有效地将分布较为相似的数据划分到同一个区域, 而且分布相似的点进行Hilbert编码以后, 可以使模型更容易学习, 精度更高.
根据上述分析可知, 我们需要在降维处理前, 先对空间数据进行聚类, 按照聚类结果, 将空间划分成不同的子区域, 使得在相同子区域内, 数据分布较为相似, 不同子区域内数据分布不同. 在划分结果上进行多段线性模型的训练, 不仅可以提高训练速度, 更可以提升模型的精确度. 本文采用基于划分的聚类算法K-means, 这是一种简单有效的无监督学习算法, 可以快速实现区域划分, 而且最大限度地保证数据区分度. 由于高维数据存在维度诅咒的问题, 即当数据维度过高时, 各数据点直接的距离会趋于一致使得一般距离公式失效的现象. 所以K-means需要根据数据的维度对距离公式进行选择, 当数据维度较低时采用较为简单的欧式距离, 数据维度过高时采用余弦相似性. 算法1展示了数据空间划分的过程. 显然, 作为K-means的超参数, K值的设定会影响索引的效率, 设定过大的K值可以使得空间被划分成很多区域, 每个区域内数据量小, 模型精度高, 但是训练大量模型会造成极大的开销; 设定过小的K值, 会使得每个区域内数据量较大, 模型精度难以保证. 不同的数据分布需要设定不同的K值, 在实验部分我们将进行详细的说明. 除此之外, 当数据量太大时, 也可以使用K-means的各种优化版本进行优化.
算法1展示具体的聚类及空间区域划分的过程. D为空间数据集, 首先根据K-means算法进行迭代, 计算每个数据点与所有中心点的距离, 选择与其距离最近的簇作为自己的标签, 全部数据计算之后, 更新聚簇中心点, 再次迭代全部数据, 直至聚类簇不发生改变为止. 最后根据聚类返回的聚簇中心点和聚簇边界, 将数据空间划分成K个部分.
算法1. 空间区域划分过程.
输入: 数据空间的全部高维数据D =
输出: 子空间区域P =
初始化: 随机选择K个点作为聚类中心
1. 重复以下过程直到聚类簇不发生变化{
2. 对于每个数据点d, 计算其与所有聚类中心之间的最小距离:
3.
4. 将d分配到第i簇;
5. 对于每个簇重新计算中心点}
6. 计算每个聚类中心与该聚簇中数据的最远距离:
7.
8.
本节详细介绍IHDL索引的降维与模型训练过程. 第2.1节的空间区域划分, 已经将整个高维空间划分成了K个部分. 接下来就是针对每个区域进行降维处理, 并对降维的数据进行模型训练. 在一维空间中, 数据之间有自然的大小关系, 对于范围查询只要返回两个边界点之间的全部数据即可, 但是高维数据本身没有固定的相对大小, 无法进行有规则的排序, 学习型索引只适用于有序数据, 所以需要运用Hilbert的映射方式, 将高维数据映射成一维.
如图3所示, Hilbert曲线是一条可以将整个空间填充的曲线, 其构造方式是把前一阶的曲线复制4份, 将左下角和右下角的曲线做一个沿对角线的翻转, 然后增加3条线段把这4份连起来, 这样一直划分的极限就是Hilbert曲线. 该曲线将高维空间的数据点全部串连起来, 使得高维数据有了固定的排序, 这样就可以实现高维数据向一维的映射. 除此之外, Hilbert曲线还具有很好的聚集性, 在空间中相近的点在Hilbert曲线上也一定相近, 这就使得编码后的数据保留了原始数据的分布特点.

|
图 3 1–3阶2维Hilbert曲线 |
Hilbert降维就是根据数据点在Hilbert曲线上的位置即Hilbert编码, 将其降成一维. Hilbert编码的计算过程为: 首先确定高维数据在1阶Hilbert曲线的所在位置, 然后一直迭代至Hilbert初始化的最高阶, 将该数据点在各阶中位置的二进制编码连起来就是其在Hilbert曲线上的编码. 例如数据点(5, 2)在3阶Hilbert曲线上的编码, 首先点(5, 2)在1阶曲线上, 位于2的位置, 二进制为10, 然后在2阶曲线位于0的位置, 二进制为00, 最后在3阶曲线上位于2的位置, 二进制为10, 将二进制编码连起来100010, 即为点(5, 2)的3阶Hilbert编码, 转换为十进制是34.
对于已经降至一维的数据, 首先我们尝试使用全连接神经网络进行拟合, 用Hilbert编码作为神经网络的输入, 数据在一维序列里的位置作为每个数据的标签, 神经网络采用双隐藏层, 采用ReLU做激活函数进行非线性变换, 用预测值与真实值的均方差(MSE)做代价函数, 对模型进行多次训练循环, 尽可能降低每个分区内模型的预测误差.
在采用神经网络做模型时, 训练开销很大, 需要花费大量时间来拟合数据. 除此之外, 每个网络的误差并不相同, 所以需要为每个模型维护一个误差边界, 这样就造成了模型精度的不一致, 在预测值两侧进行二分查找的范围难以统一, 而且对于误差较大的模型, 查找时间较长. 当分区内数据量较小的时候, 降维数据的线性特征较为明显, 所以并不需要训练有非线性变换的神经网络. 采用多段线性模型来拟合降维后的数据分布不仅可以满足精度要求, 更可以减少模型训练的复杂度、提高查询速度、减少模型的训练时间. 多段线性模型的构建过程采用自适应树[9]中提及的思路, 对一维有序数列进行遍历, 增量式地进行构建, 判断每个节点是否满足前一个线性函数预设的误差边界, 如果不满足就以该节点为起点, 构建新的一个线性函数, 最后将所有线性函数的起点和斜率存到树形结构中. 具体算法如算法2所示. 多段线性模型的分段依据是误差边界, 所以只需要控制误差边界的大小就可以保证模型的准确性, 例如当误差边界与R树的节点容量相同时, 可以看作其准确性与R树相同. 除此之外, 多段线性模型也统一了每个分区的误差边界, 极大地减少模型训练带来的不确定性. 在本文实验部分还对误差边界对查询效率的影响进行了实验分析, 来对比不同误差小查询效率的变化. 多段线性模型的构造复杂度为O(n), 远小于复杂神经网络的训练复杂度, 可以大幅减少模型训练所带来的开销.
算法2. 多段线性模型训练过程.
输入: 一维的Hilbert编码keys, 一维数据中的位置pos, 误差边界err;
输出: 多段线性模型.
初始化: 第一个key作为第一段的起点,
1. 对keys中的每一个k做如下操作{
2. 如果
3. 更新
4.
5.
6. 否则k作为新的起点, 初始化
在介绍查询过程前需要先介绍Hilbert曲线的非封闭性. 其定义如下所示.
定义1. 非封闭性. 给定一个封闭区域, 与一条无限长的曲线, 若曲线的两个端点总是在封闭区域的边界外, 则称该曲线满足非封闭性.
第2.2节提到, 在降维数据上训练得到K个独立的模型, 而且所有模型都有共同的误差边界, 使用索引进行查询时, 首先定位与查询相关的空间区域, 计算每个相关区域内与查询区域的交集. 由于Hilbert曲线满足非封闭性, 所以对于给定的查询超矩形, Hilbert曲线一定会与超矩形相交, 这就使得该超矩形内数据的Hilbert编码最大值与最小值必然出现在查询矩形的边界上. 所以范围查询可以转换成两次点预测, 只需要计算交集边界上的Hilbert编码最大最小值, 然后在线性模型中分别进行预测, 返回预测值
另外, 如果直接对所有空间区域进行相交判断会产生较高的计算开销, 所以要首先对可能相交的区域进行预筛选, 在可能相交的区域里计算交集. 预筛选的流程是, 首先对空间区域从左下到右上进行编号, 然后计算查询范围的左下点和右上点所在区域编号, 两个编号之间的所有区域即为可能相交区域. 这样可以一定程度上减少与查询无关区域的访问.
IHDL不仅实现了常见的范围查询, 它采用查询转换的方法将最近邻查询转换成范围查询以此来实现最近邻查询. 如算法3所示, M为数据区域的数据密度, 在查询转换的时候, 首先根据分区内的数据密度预测一个初始的查询范围, 返回该范围内距离查询点最近的前K个数据点. 如果范围内点数量小于K, 则再次根据数据密度将查询范围逐渐扩大, 直至返回全部满足条件的数据. 算法平均复杂度为O(m×K), 其中m为进行范围查询的次数, K为最近邻查询点数量.
算法3. 最近邻查询转范围查询.
输入: 查询点p, 查询数据量k;
输出: 距离点p最近的k个数据点.
1. 选择p所在空间区域
2.
3. 在以p为中心边长为d的区域内做范围查询
4. 如果返回数据量不足k:
5. 则迭代d = d + △d, 重复做范围查询, 直到返回数据量大于k, 选择距离p最近的k个数据点
6. 如果返回数据量超过k:
7. 返回离p最近的k个数据点
3 实验评估本节, 我们通过一系列实验评估IHDL索引的性能, 并与R树、四叉树、ZM索引、Flood索引在构建时间、查询效率、索引内存占用等方面进行对比, 从而验证本文模型的有效性. 同时对比了运用神经网络的模型IHDL_DNN和多段线性模型的IHDL索引的性能. 基准索引如下.
(1) ZM索引: 分为两层的递归模型, 顶层模型为两个隐藏层的全连接神经网络, 隐藏层的神经元数为64×64, 底层是神经元为32×32的全连接神经网络, 每个隐藏层后用ReLU层做非线性变换, 顶层的输入为Z地址, 输出为底层的模型编号, 底层模型的输入也是Z地址, 输出为查询数据所在的位置.
(2) Flood索引: 根据数据分布对空间做均匀切分, 并对每个网格内数据根据同一纬度做排序, 使用两个隐藏层的递归模型做预测, 隐藏层神经元数为64×64, 隐藏层后使用ReLU函数做非线性变换.
(3) R树: 每个节点包含的最大记录数为200.
(4) 四叉树: 最大空间区域为(0, 0)到(100000, 100000).
为保证实验公平性, 所有实验在一台Intel(R) Xeon(R) Gold 5118 CPU @ 2.30 GHz服务器上进行, 所有的索引结构都用Python 3.8编程实现, 并用单线程在CPU上运行, 其中有关的神经网络模型使用PyTorch实现. IHDL索引具体的默认模型设置参数如下:
(1) IHDL: K值为10, 误差边界为200;
(2) IHDL_DNN: K值为10, 网络为3个隐藏层的全连接模型, 隐藏层神经元数为50×100×50, 损失函数为预测值与真实值的均方误差, 非线性变化为ReLU
本文实验采用两个不同的数据集进行对比验证, 分别是随机生成满足正态分布的人工数据集(Random)和真实的地图数据集(OSM). 其中人工数据集为200万条无重复数据; 地图数据集采用OSM的数据, 选取深圳市南山区内建筑与地名数据记录, 提取其中的经纬度作为关键字, 记录数为100万条, 大小为160M, 数据方差较小, 数据分布较为密集. 由于本文实验数据的维度较低, 所以采用欧式距离作为K-means算法的距离函数. 首先针对两个数据集分别进行IHDL索引和ZM索引的模型训练, 并保存训练好的模型, 然后在两个数据集上分别构建R树与四叉树, 生成不同的查询负载, 对各索引进行性能测试; 除此之外, 本节还针对IHDL索引的两个超参数, K值和误差边界进行查询性能对比.
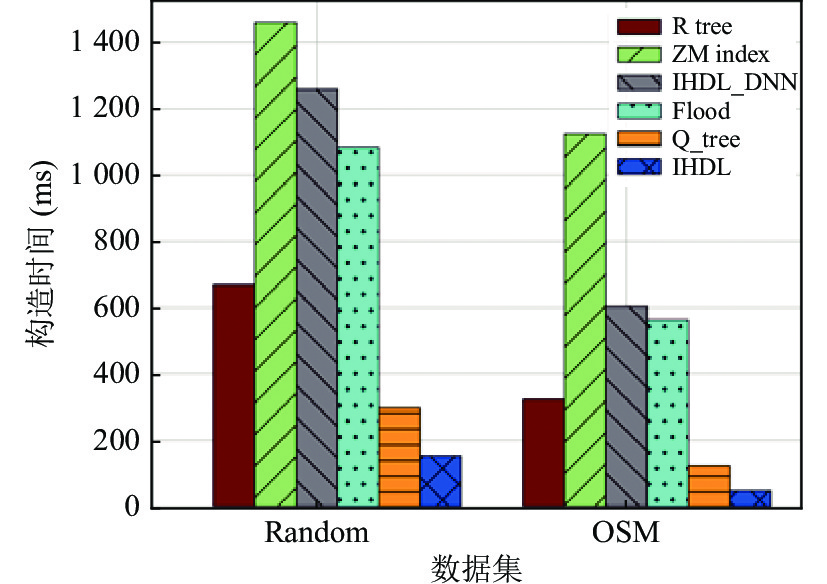
3.1 索引构造时间对比本节实验测试了IHDL索引、IHDL_DNN、R树、四叉树、ZM索引、Flood索引的构建时间, 如图4所示, 横坐标为不同的数据集, 纵坐标为索引构建时间, 构建时间越短, 说明索引的初始化越快. 可以看出在两个数据集上, IHDL索引、R树和四叉树的构建速度都远超过ZM索引、Flood索引和IHDL_DNN模型, 这是因为ZM索引与Flood索引采用神经网络构成的层次模型, IHDL_DNN采用全连接网络做降维数据拟合的模型, 它们为了保证查询精确度需要进行大量的训练循环, 在每个循环中会进行大量计算, 使得索引构造时间较长. 在Random数据集上IHDL的构造速度比R树提升了77.3%, 比四叉树提升了50%, 比IHDL_DNN提升了88%, 比ZM索引提升了92.9%, 比Flood索引提升了85.9%; 在OSM数据集上IHDL索引的构造速度比R树提升了85%, 比四叉树提升了62%, 比IHDL_DNN提升了92%, 比ZM索引提升了95%, 比Flood索引提升了91%.
|
图 4 索引构造时间对比 |
由图4可得, 在两个数据集上, IHDL索引的构造时间均远小于R树与四叉树. 这是由于R树结构是平衡树, 在构造的时候需要保持结构的动态平衡, 在R树中, 当节点内数据量超过最大值时会有节点的分裂过程, 而且底层的节点分裂会导致顶层节点内数据发生改变, 顶层节点也会动态调整, 这就会产生较大的时间开销. 在四叉树中需要对数据空间进行不停地四等分, 构建索引的时候, 也会存在大量的节点分裂过程, 从而消耗较多时间. 对于IHDL索引来说, 只需要将数据读入并进行一次降维, 在对降维数据进行训练的时候, 采用的是多段线性模型, 增量式的训练过程中, 只需要对降维数据进行一次遍历, 时间复杂度为O(n), 这样就可以节省大量的构建时间. 在OSM数据集上IHDL索引的构建时间远小于Random数据集, 这是因为OSM是真实数据集, 其数据的聚集性更好, 进行空间区域划分以后, 每个区域内的数据分布更加接近, Hilbert编码的线性规律更明显, 多段线性函数的训练过程更快.
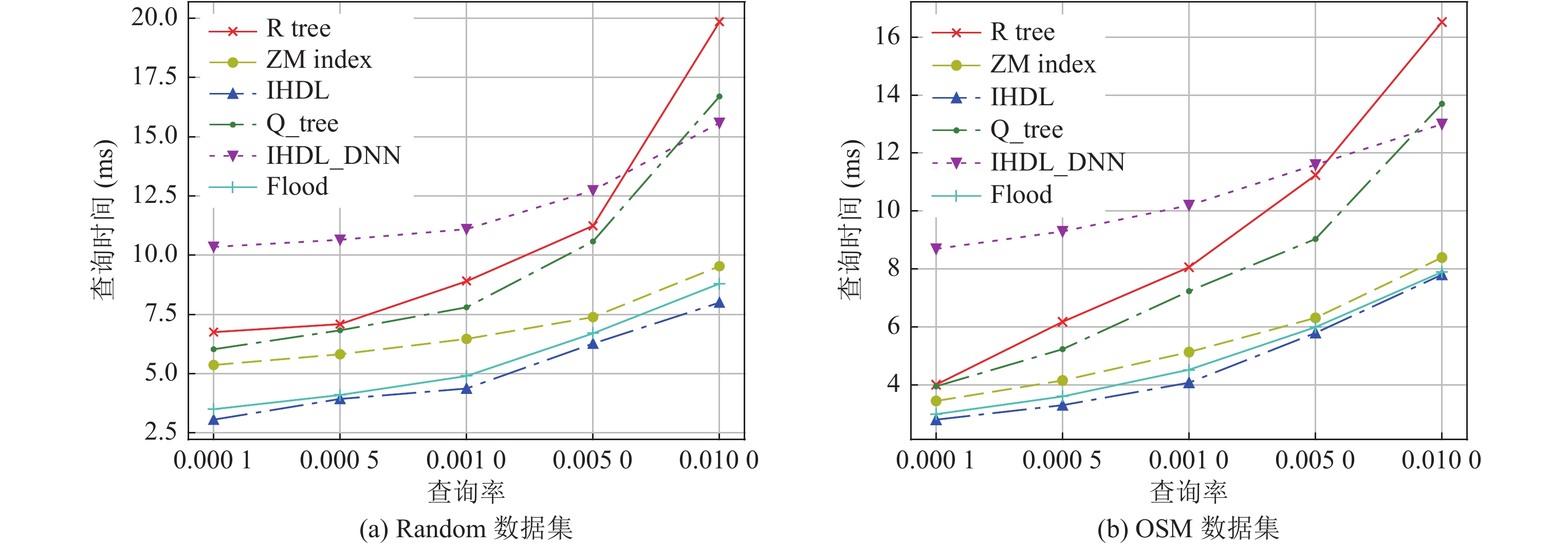
3.2 查询性能对比本节对比了3种索引在不同查询选择率下的范围查询性能, 查询选择率设置为0.0001到0.01, 这里的查询选择率为查询返回的数据条目占总数据量的比例, 即每个查询涉及的数据条目数. 对于每个查询选择率, 我们随机生成50条不同的查询计算其平均查询时间. 实验结果如图5所示, 横轴为查询率, 设置为0.0001、0.0005、0.001、0.005、0.01等值, 纵轴为平均单次查询的时间, 单位为ms. IHDL索引的K值设置为10, 误差边界设置为200.
|
图 5 索引查询时间对比 |
实验结果显示, 在两个数据集上, 采用全连接网络的IHDL_DNN模型效果较差, 查询效率低于其他索引类型. 这是因为只用神经网络模型对每个分区进行学习, 拟合效果较差, 误差边界难以控制, 进而影响查询速度, 而且模型内部神经元设计较为复杂, 降低了查询速度.
采用多段线性模型的IHDL索引、ZM索引与Flood索引的查询速率均远超过R树, 这是因为两种索引采用的模型都十分简单, 进行查询时只会进行少量的计算, 而R树需要在节点内进行查询比较, 并不停地迭代节点, 当数据量较大的时候, R树层次会变得越来越复杂, 但是学习型索引的模型不会明显变化. 除此之外, 对于CPU来说, 计算速度比查询比较速度更快. 所以学习型索引的查询速度相较于传统索引结构R树可以得到大幅度提升.
由图5(a)、5(b)可得, 在两个数据集上, IHDL索引的查询性能均优于ZM索引. 在Random数据集上, 查询选择率较小时(0.0001), IHDL查询性能比ZM索引提升了40%, 而查询选择率较大时(0.01), IHDL只比ZM索引提升了17%. 这是因为当查询选择率变大的时候, 查询范围逐渐变大, 返回的数据条目数变多, 而Hilbert编码的速度相较于Z编码更慢, 随着数据条目的增加, 在编码上消耗的时间会逐渐增加, 总的查询速度就会下降. 在OSM数据集上, 查询选择率较小的时候(0.0001), IHDL查询速率比ZM索引提升了19%, 当查询选择率变大以后, IHDL比ZM索引提升了7%.
在两个数据集上进行对比可知, IHDL索引的查询性能均优于Flood索引. 在Random数据集上, IHDL查询性能比Flood最大提升了14.3%, 在OSM数据集上IHDL查询性能比Flood索引最大提升了6.7%. 这是由于Flood索引使用了更为复杂的层次模型, 相较于IHDL的多段线性模型会耗费更多的时间. 与ZM索引对比结果相似, 随着查询选择率的增大, IHDL的提升幅度逐渐降低, 造成这一现象的原因仍然是Hilbert编码的速度.
在OSM数据集上的提升水平低于Random数据集的原因是, 所选用OSM数据集的数据整体分布较为密集, Z编码也较为接近, 由上文可知IHDL索引首先对空间区域进行划分, 然后对子区域做Hilbert降维, 在全部数据比较集中的数据集上, IHDL索引的空间区域划分优势并不明显, 对数据空间划分以后并不能大幅度减少无效数据的搜索.
3.3 索引内存占用对比本节对比了R树、四叉树、ZM索引、Flood索引、IHDL_DNN以及IHDL索引在不同数据集上的内存占用情况, 结果如表1所示. 可以看出学习型索引在两个数据集上都可以保证规模远小于传统索引R树与四叉树. 这是因为学习型索引只需要存放模型的主要参数, 不需要对原始数据进行存储, 模型参数的数据规模远小于原始数据, 而R树需要存储全部数据的最小外接矩形, 叶节点内还需要存放数据信息, 四叉树需要按照空间四分的格式存放原始, 所以二者的内存开销均远大于学习型索引.
| 表 1 索引内存占用对比 |
由实验结果可得, 在Random数据集上IHDL索引内存占用比ZM索引降低了79%, 比Flood索引降低了82%, 比R树降低了99%, 比四叉树降低了99%, 比IHDL_DNN降低了70%; 在OSM数据集上IHDL索引内存占用比ZM索引降低了86%, 比Flood索引降低了88%, 比R树降低了99%, 比四叉树降低了99%, 比IHDL_DNN降低了78%. IHDL索引内存优化强于ZM索引与Flood索引, 这是由于IHDL索引所用的模型为多段线性模型, 对于每个子区域, 只需要存储每段线性模型的起点和斜率, 这就使得整体的模型参数大幅度减少. 而ZM索引与Flood索引均采用递归模型, 由多个神经网络构成, 又由于精度要求, 需要存储每个全连接神经网络的全部参数, 每个网络都有数百个参数, 所以ZM索引与Flood索引的存储规模远超过IHDL索引, 需要消耗更多的内存空间.
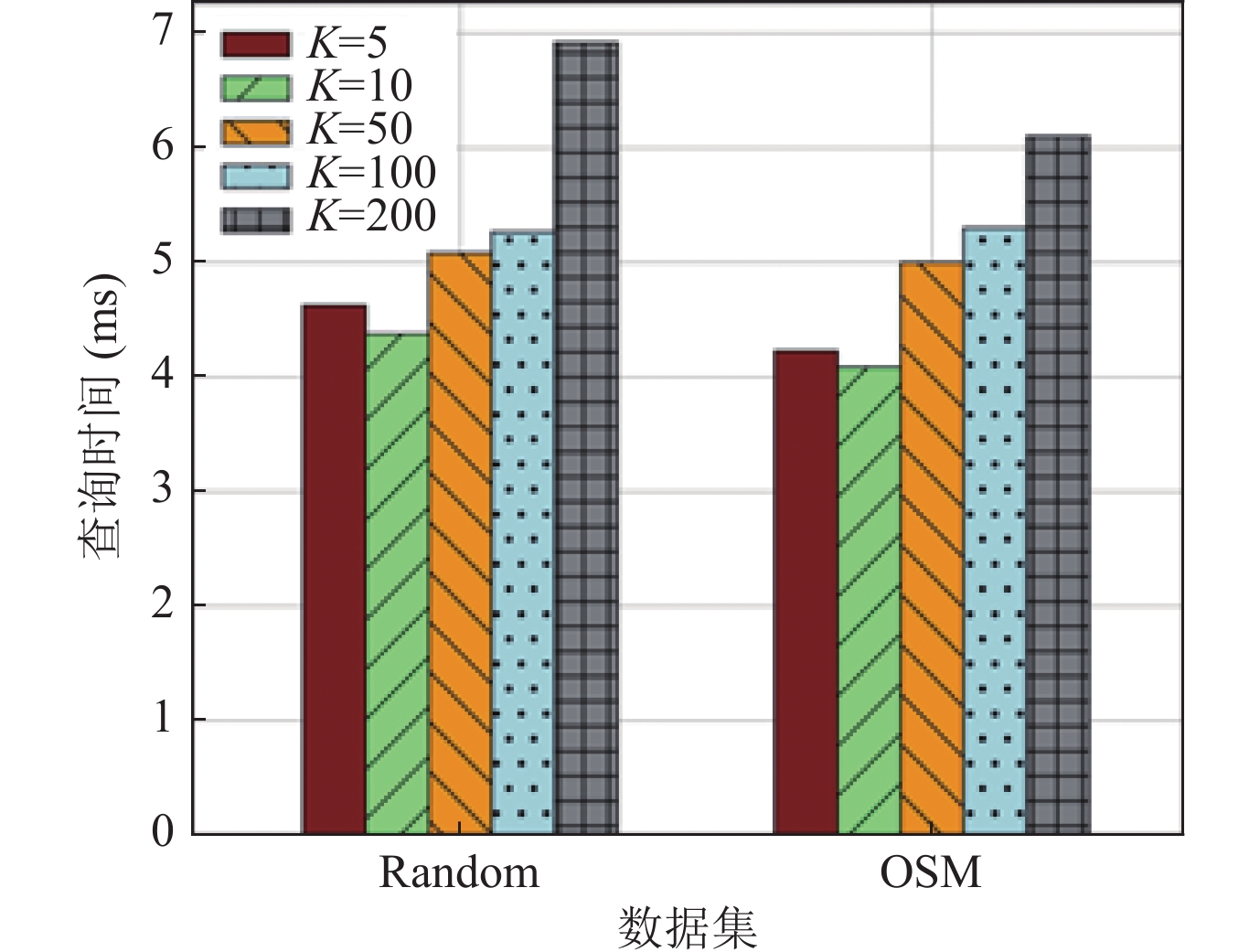
3.4 K值设定对IHDL索引的影响本节针对不同K值, 即不同的区域划分数量, 对IHDL索引的性能进行比较. 我们仍然选择在两个不同数据集上进行对比, 查询选择率设置为0.001, 误差边界设置为200. 实验K值设置为10、50、100、500等4组. 实验结果如图6所示, 横轴均为数据集, 纵轴为平均单次查询时间, 单位为ms.
|
图 6 不同K值时的查询时间对比 |
由图6可知, 在两个数据集上, 过大的K值, 均会降低查询效率, 这是由于空间区域划分数量过多, 会增大查询相关区域判断的复杂度, 而单个区域内的查询并不会大幅度提速, 所以导致整体的查询速率下降. 除此之外, 较低的K值也会使得查询速率下降, 这是因为, K值较小, 没有很好地将数据区分开, 导致每个区域内的查询变慢. 所以K值应该在保证数据区分度的情况下尽可能小.
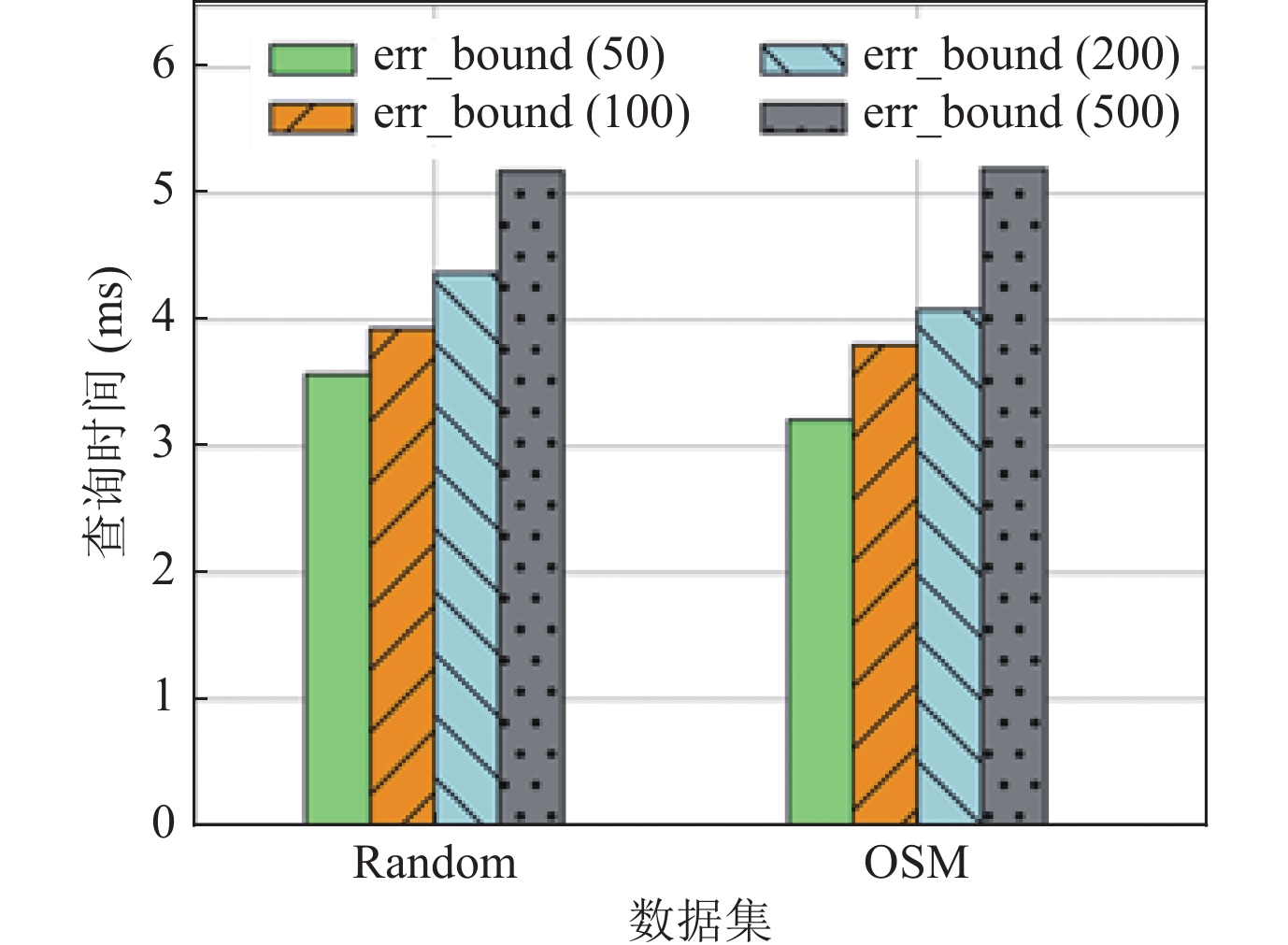
3.5 误差边界对IHDL索引的影响本节针对不同的误差边界, 对IHDL索引的性能进行比较. 查询选择率设置为0.001值, K值设置为10. 实验的误差边界设置为50, 100, 200, 500等4组. 实验结果如图7所示. 横轴是数据集, 纵轴为平均单次查询时间, 单位为ms.
|
图 7 不同误差边界时的查询时间对比 |
实验结果可得, 在两个数据集上, 随着误差边界的增大, 查询时间均会变大. 这是由于, 当误差边界增大时, 在预测点两侧的查询范围会变大, 会增大无效搜索范围, 需要消耗更多的时间, 查询速率会降低. 当误差边界无限变大的时候就相当于把索引结构退化成了普通的二分查找, 所以应当在不影响模型学习的前提下尽可能降低误差边界.
3.6 实验结论我们对比了不同数据集下多种索引结构的查询性能, 构造速度, 以及内存占用, 实验结果如下.
在Random数据集上, IHDL索引的查询性能比R树提升了60%, 比四叉树提升了50%, 比ZM索引最大提升了40%; 同时, 在内存占用方面比ZM索引降低了79%, 比四叉树降低了99%, 比R树降低了99%. 除此之外, IHDL的构造速度比R树提升了77.3%, 比四叉树提升了50%, 比ZM索引提升了92.9%.
在OSM数据集上, IHDL索引的查询性能比R树最大提升了52%, 比四叉树最大提升了43%, 比ZM索引最大提升了19%; 同时, 在内存占用方面比ZM索引降低了86%, 比四叉树降低了99%, 比R树降低了99%, 索引的构造速度比R树提升了85%, 比四叉树提升了62%, 比ZM索引提升了95%.
另外我们还比较了不同K值和误差边界对IHDL索引性能的影响, 由实验结果可得, K值与误差边界均会对IHDL索引的查询性能产生影响, 而且会影响索引构建的时间, 如何有效地选择K值与误差边界需要结合数据分布进行考虑.
4 总结与展望如何高效地对数据进行检索是数据库领域的热点. 文献[8]提出用深度学习的模型代替传统索引结构后, 学习型索引取得了诸多显著成就, 索引的检索效率得到了极大的提高. 将学习型算法应用到高维数据上以后, 虽然对索引效率有所提高, 但是由于所用技术的限制, 不能完全利用数据分布的信息. 本文提出的IHDL索引, 结合了现有技术的优势, 可以更好地对数据分布进行学习, 而且可以实现范围查询和最近邻查询等多种查询方式. IHDL采用3种处理机制: 首先根据K-means聚类结果对数据空间进行划分, 将数据空间划分成K个区域; 然后在每个区域分别进行Hilbert降维处理, 针对降维数据训练多段线性模型; 最后在进行查询的时候, 运用查询转换实现多种查询方式. 通过不同数据集的实验验证, 与其他索引结构相比, IHDL索引在构建时间, 查询速度, 内存占用等方面均取得了显著提升. K值与误差边界能够明显影响IHDL索引的性能, 是重要的超参数, 决定了空间被划分的数量与多段线性模型的精确度, 设定过大或过小都会使得索引效率下降, 所以在未来的工作中, 可以从理论的角度分析两个超参数的最佳取值; 另外, IHDL索引本身并未对索引更新进行探索, 在未来我们会从理论和实验的角度分析更优的索引存储方式, 来提高索引的更新效率, 减少模型重新训练的负担.
| [1] |
Sun LM, Zhang SM, Ji T, Li CP, Chen H. Survey of data management techniques powered by artificial intelligence. Ruan Jian Xue Bao/Journal of Software, 2020, 31(3): 600−619. http://www.jos.org.cn/1000-9825/5909.htm (in Chinese with English abstract)
|
| [2] |
Beckmann N, Kriegel HP, Schneider R, Seeger B. The R*-tree: An efficient and robust access method for points and rectangles. In: Proc. of the 1990 ACM SIGMOD Int’l Conf. on Management of Data. Atlantic City: Association for Computing Machinery, 1990. 322–331.
|
| [3] |
Sellis TK, Roussopoulos N, Faloutsos C. The R+-tree: A dynamic index for multi-dimensional objects. In: Proc. of the 13th Int’l Conf. on Very Large Data Bases. Brighton: Morgan Kaufmann Publishers Inc., 1987. 507–518.
|
| [4] |
Jung HR, Kim YS, Chung YD. QR-tree: An efficient and scalable method for evaluation of continuous range queries. Information Sciences, 2014, 274: 156-176.
[doi:10.1016/j.ins.2014.02.061] |
| [5] |
Finkel RA, Bentley JL. Quad trees a data structure for retrieval on composite keys. Acta Informatica, 1974, 4(1): 1-9.
[doi:10.1007/BF00288933] |
| [6] |
Samet H. The quadtree and related hierarchical data structures. ACM Computing Surveys, 1984, 16(2): 187-260.
[doi:10.1145/356924.356930] |
| [7] |
Samet H. Foundations of Multidimensional and Metric Data Structures. San Francisco: Morgan Kaufmann Publishers Inc., 2005.
|
| [8] |
Kraska T, Beutel A, Chi EH, Dean J, Polyzotis N. The case for learned index structures. In: Proc. of the 2018 Int’l Conf. on Management of Data. Houston: Association for Computing Machinery, 2018. 489–504.
|
| [9] |
Galakatos A, Markovitch M, Binnig C, Fonseca R, Kraska T. FITing-tree: A data-aware index structure. In: Proc. of the 2019 Int’l Conf. on Management of Data. Amsterdam: Association for Computing Machinery, 2019. 1189–1206.
|
| [10] |
Ding JL, Minhas UF, Yu J, Wang C, Do J, Li YN, Zhang HT, Chandramouli B, Gehrke J, Kossmann D, Lomet D, Kraska T. ALEX: An updatable adaptive learned index. SIGMOD. In: Proc. of the 2020 ACM SIGMOD Int’l Conf. on Management of Data. Portland: Association for Computing Machinery, 2020. 969–984.
|
| [11] |
Li PF, Hua Y, Zuo PF, Jia JN. A scalable learned index scheme in storage systems. arXiv:1905.06256, 2019.
|
| [12] |
Ferragina P, Vinciguerra G. The PGM-index: A fully-dynamic compressed learned index with provable worst-case bounds. Proc. of the VLDB Endowment, 2020, 13(8): 1162-1175.
[doi:10.14778/3389133.3389135] |
| [13] |
Li X, Li JD, Wang XL. ASLM: Adaptive single layer model for learned index. In: Proc. of the 2019 Int’l Conf. on Database Systems for Advanced Applications. Chiangmai: Springer, 2019. 80–95.
|
| [14] |
Wang YY, Tang CZ, Wang ZG, Chen HB. SIndex: A scalable learned index for string keys. In: Proc. of the 11th ACM SIGOPS Asia-Pacific Workshop on Systems. Tsukuba: Association for Computing Machinery, 2020. 17–24.
|
| [15] |
Macke S, Beutel A, Kraska T, Sathiamoorthy M, Cheng DZ, Chi EH. Lifting the curse of multidimensional data with learned existence indexes. In: Proc. of the 32nd Conf. on Neural Information Processing Systems. Montréal, 2018.
|
| [16] |
Van Sandt P, Chronis Y, Patel JM. Efficiently searching in-memory sorted arrays: Revenge of the interpolation search. In: Proc. of the 2019 Int’l Conf. on Management of Data. Amsterdam: ACM, 2019. 36–53.
|
| [17] |
Qu WW, Wang XL, Li JD, Li X. Hybrid indexes by exploring traditional B-tree and linear regression. In: Proc. of the 16th Int’l Conf. on Web Information Systems and Applications. Qingdao: Springer, 2019. 601–613.
|
| [18] |
Hadian A, Heinis T. Interpolation-friendly B-trees: Bridging the gap between algorithmic and learned indexes. In: Proc. of the 22nd Int’l Conf. on Extending Database Technology. Lisbon: OpenProceedings.org, 2019. 710–713.
|
| [19] |
Llaveshi A, Sirin U, Ailamaki A, West R. Accelerating B+tree search by using simple machine learning techniques. In: Proc. of the 1st Int’l Workshop on Applied AI for Database Systems and Applications. Los Angeles, 2019.
|
| [20] |
Wang HX, Fu XY, Xu JL, Lu H. Learned index for spatial queries. In: Proc. of the 20th IEEE Int’l Conf. on Mobile Data Management (MDM). Hong Kong: IEEE, 2019. 569–574.
|
| [21] |
Jagadish HV, Ooi BC, Tan KL, Yu C, Zhang R. iDistance: An adaptive B+-tree based indexing method for nearest neighbor search
. ACM Trans. on Database Systems, 2005, 30(2): 364-397.
[doi:10.1145/1071610.1071612] |
| [22] |
Davitkova A, Milchevski E, Michel S. The ML-Index: A multidimensional, learned index for point, range, and nearest-neighbor queries. In: Proc. of the 23rd Int’l Conf. on Extending Database Technology (EDBT). Copenhagen: OpenProceedings.org, 2020. 407–410.
|
| [23] |
Nathan V, Ding JL, Alizadeh M, Kraska T. Learning multi-dimensional indexes. In: Proc. of the 2020 ACM SIGMOD Int’l Conf. on Management of Data. Portland: Association for Computing Machinery, 2020. 985–1000.
|
| [24] |
Li PF, Lu H, Zheng Q, Yang L, Pan G. LISA: A learned index structure for spatial data. In: Proc. of the 2020 ACM SIGMOD Int’l Conf. on Management of Data. Portland: Association for Computing Machinery, 2020. 2119–2133.
|
| [25] |
Dong YH, Indyk P, Razenshteyn IP, Wagner T. Learning space partitions for nearest neighbor search. In: Proc. of the 8th Int’l Conf. on Learning Representations. Addis Ababa: OpenReview.net, 2020.
|
| [26] |
Ding JL, Nathan V, Alizadeh M, Kraska T. Tsunami: A learned multi-dimensional index for correlated data and skewed workloads. Proc. of the VLDB Endowment, 2020, 14(2): 74-86.
[doi:10.14778/3425879.3425880] |
| [27] |
Hadian A, Ghaffari B, Wang TY, Heinis T. COAX: Correlation-aware indexing on multidimensional data with soft functional dependencies. arXiv:2006.16393. 2020.
|
| [28] |
Qi JZ, Liu GL, Jensen CS, Kulik L. Effectively learning spatial indices. Proc. of the VLDB Endowment, 2020, 13(12): 2341-2354.
[doi:10.14778/3407790.3407829] |
| [1] |
孙路明, 张少敏, 姬涛, 李翠平, 陈红. 人工智能赋能的数据管理技术研究. 软件学报, 2020, 31(3): 600−619. http://www.jos.org.cn/1000-9825/5909.htm
|