极致的图片真实感一直以来都是三维图形渲染技术追求的目标之一. 历经了几十年的发展, 现代图形渲染技术无论是在图片画质还是运算性能方面都产生了巨大的革新, 也已成功应用到包括电视电影特效、军事仿真环境、工业数字孪生以及三维电子游戏等很多领域. 遗憾的是, 时至今日, 我们依然看到大多数渲染器所生成的图片尚不能达到以假乱真的程度, 它们模拟的效果和物理世界真实的效果还存在一定的差距. 这其中最具代表性的就是参与介质(participating media)的模拟和渲染[1−3]. 图 1列举了近期一些电影、游戏以及仿真系统中的参与介质渲染效果.

|
图 1 近期电影、游戏和仿真系统中的参与介质(皮肤、云、雾、水体)渲染效果 |
参与介质在自然界中无处不在, 从广袤天空中的云层、烟雾到深邃大海中的水体、气泡, 从日常的水果、衣物到高贵的翡翠、玛瑙, 都属于参与介质. 甚至人体的皮肤也是一种复杂的参与介质. 虽然参与介质在现实世界大量存在, 其渲染方法也已被研究了很多年, 但是时至今日, 很多渲染器都无法高效地处理这些参与介质, 尤其是应用于实时环境(要求每秒钟生成至少30张图片)的高性能渲染器. 因此, 当前很多实时类图形应用系统中都尽量避免使用参与介质, 或者用高度近似的方法处理. 这导致参与介质在很多应用中显得比较失真, 如图 1(c)中对海水的模拟. 产生这个问题的主要原因在于: 1) 参与介质本身的结构非常复杂; 2) 光线在参与介质中的传播过程非常复杂.
为了缓解这些复杂性带来的压力, 目前, 几乎所有的渲染器在处理参与介质时都会基于两点基本假设: 独立散射(independent scattering)假设和局部连续(local continuity)假设. 前者意味着每根光线和参与介质交互都是独立的行为, 可以单独处理而不用考虑其他光线; 后者则认为参与介质在任意一个局部微体积内都是同质均匀的. 在这两点假设下, 经典的辐射传输方程(radiative transfer equation, RTE)[7]成立. 这个方程也是几乎所有渲染器处理参与介质的理论基础. 本文把基于上述两点假设的渲染方法称为经典的参与介质渲染方法.
但是, 大量的物理事实以及物理学中的研究表明: 这两点假设只是对自然界中真实介质的一定程度的近似, 虽然在一些涉及参与介质的场景渲染中取得了成功, 但是并不能处理所有的参与介质. 尤其是在追求更高画质的前提下, 需要打破这两个假设条件, 用更符合物理客观规律的方式来处理参与介质. 为区别于经典的参与介质渲染方法, 我们把这类处理方式称为非经典的参与介质渲染方法. 这意味着我们在处理参与介质时, 要考虑非独立散射(也称相干散射)和局部不连续性(也称离散粒子性). 为了进一步提升参与介质渲染的物理真实感, 近年来, 学术界在这方面的研究工作日益增多, 相关技术也越来越吸引工业界的关注. 本文将介绍和分析这一领域现有的一些研究工作. 迄今为止, 国内外已有一些面向传统的参与介质渲染方法的综述性文章, 如文献[1−3], 但这些文献很少涉及相干介质(打破第1点假设)或离散介质(打破第2点假设)的渲染方法的介绍. 而处理这些新介质类型带来了新的思想、新的模型和新的技术. 因此, 本文是对已有的参与介质渲染方法综述性文章的补充和扩展.
本文首先简单回顾一下经典的参与介质渲染技术, 阐述一些基本的概念和代表性技术; 然后, 详细分析现有的参与介质渲染方法中的两个基本假设: 独立散射假设和局部连续假设; 接着, 分别分析和讨论现有的相干介质渲染方法和离散介质渲染方法; 最后, 展望一些开放性问题并进行总结. 本文综述希望能启发相关领域的研究人员进一步攻克非经典的参与介质渲染技术中的关键问题和技术难点, 也为工业界改进现有渲染器以提高参与介质渲染的真实感提供参考.
1 经典的参与介质渲染技术为了更好地理解非经典的参与介质处理方式, 本节简要回顾经典的参与介质渲染技术, 尤其是阐述基本概念和分析代表性技术. 这个方向更多的内容可以参考综述文献[1−3].
1.1 基本概念(1) 吸收和散射
我们假设参与介质都是由大量的微小粒子组成的. 当一束光线射入参与介质时, 光线和参与介质中的微小粒子将发生各种复杂的交互行为, 其中最主要的是光的吸收和散射. 当光吸收现象发生时, 光线的能量并非消失, 而是转化为另一种能量形式(例如热能). 参与介质吸收光线能量的能力可以用吸收系数(absorption coefficient) σa描述. 通常情况下, 吸收系数是粒子的吸收截面(absorption cross section) Ca和粒子数量浓度N的乘积, 即σa=CaN. 当光散射现象发生时, 入射光线因粒子的存在而发生方向偏转, 导致沿着原入射方向能量损失, 其能力可用散射系数(scattering coefficient) σs刻画. 同样存在σs=CsN, 其中, Cs是散射截面(scattering cross section). 光的吸收和散射都会使得一部分能量从一束光线中消失, 因此, 可以定义消光系数(extinction coefficient) σt=σa+σs. 消光系数反映了入射光线进入介质后, 在单位距离内和粒子发生碰撞的概率. 反射率(albedo) α=σs/σt则定义了发生的碰撞事件是光散射的比例. 因散射导致的散射光线分布可用相函数(phasefunction) fP(θ)刻画, 其中, θ是散射角. 相函数满足
(2) 均匀(同质)介质和非均匀(异质)介质
若某个介质内部的吸收系数和散射系数处处相等, 则称该介质为均匀, 或同质(homogeneous)介质; 否则, 称之为非均匀, 或异质(heterogene)介质. 对于非均匀介质而言, 消光系数是位置的函数, 记为σt(x), 其中, x∈
(3) 单次散射和多次散射
单次散射和多次散射是从入射光线进入介质后到逸出介质前发生散射的次数考虑的. 通常情况下, 稀疏的介质中主要发生的是单次散射; 而稠密的介质中, 多次散射现象会大量存在. 散射次数越多, 光线传播就越复杂, 处理的难度也就越大. 但是, 当散射次数大到一定程度时, 可以用扩散(diffusion)过程[13, 14]来近似.
(4) 辐射传输方程
完整地描述光线在介质中的传播情况可以用辐射传输方程. 考虑在介质中的一束从x点出发向ω方向传播的光线, 其携带的能量用辐射率(radiance) L(x, ω)刻画. 如图 2所示: 当这束光线在介质中传播时, 有一定的概率和介质中的粒子发生碰撞, 并发生吸收或者散射现象, 这两种现象都会导致该束光线上能量的损失. 此外, 从其他光束上散射出来的能量也有可能进入该束光线, 使其能量增加. 我们通常把前后两种散射现象分别称为向外散射(out-scattering)和向内散射(in-scattering), 如图 2所示. 综合考虑这些效果, 再加上介质内的粒子可能存在的自发光(emission)现象, 我们可以用以下微分方程完整描述介质内x点处沿ω方向的能量变化:
| $ (ω⋅∇)L({\mathit{\boldsymbol{x}}}, ω)=−σ_{a}({\mathit{\boldsymbol{x}}})L({\mathit{\boldsymbol{x}}}, ω)−σ_{s}({\mathit{\boldsymbol{x}}})L({\mathit{\boldsymbol{x}}}, ω)+σ_{a}({\mathit{\boldsymbol{x}}})L_{e}({\mathit{\boldsymbol{x}}}, ω)+σ_{s}({\mathit{\boldsymbol{x}}})L_{s}({\mathit{\boldsymbol{x}}}, ω) $ | (1) |

|
图 2 光线与介质的4种交互情况 |
其中,
| $ L({\mathit{\boldsymbol{x}}}, \omega ) = \int_0^\infty {T({\mathit{\boldsymbol{x}}}, {\mathit{\boldsymbol{y}}})[{\sigma _a}({\mathit{\boldsymbol{y}}}){L_e}({\mathit{\boldsymbol{y}}}, \omega ) + {\sigma _s}({\mathit{\boldsymbol{y}}}){L_s}({\mathit{\boldsymbol{y}}}, \omega )]{\rm{d}}t} $ | (2) |
其中, y=x+tω.
| $ L({\mathit{\boldsymbol{x}}}, \omega ) = \int_0^z {T({\mathit{\boldsymbol{x}}}, {\mathit{\boldsymbol{y}}})[{\sigma _a}(y){L_e}({\mathit{\boldsymbol{y}}}, \omega ) + {\sigma _s}({\mathit{\boldsymbol{y}}}){L_s}({\mathit{\boldsymbol{y}}}, \omega )]{\rm{d}}t} + T({\mathit{\boldsymbol{y}}}, {\mathit{\boldsymbol{z}}})L({\mathit{\boldsymbol{z}}}, \omega ) $ | (3) |
其中, z=x+zω为沿着光线方向上的边界点, 即光线与不透明物体的交点. L(z, ω)表示物体表面z点的出射光辐射率, 如图 3所示. 上述方程在图形渲染中也称之为体渲染方程(volume rendering equation, VRE).
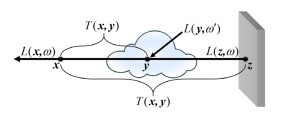
|
图 3 体渲染方程示意图 |
1.2 渲染方法
参与介质的渲染即为求解上述的体渲染方程. 由于涉及到无穷维的递归积分, 这个方程即使对于最简单的场景也无法获得解析解. 因此, 在图形渲染中通常采用数值解法. 从数值求解的方式上看, 目前的参与介质渲染方法可以分成蒙特卡洛方法和密度估计方法两大类. 当然, 还有一些面向实时应用的实时渲染方法.
(1) 蒙特卡洛方法
蒙特卡洛方法的基本思想是: 采用随机采样来求解理论上具有确定性解的体渲染方程[2], 即公式(3). 借助蒙特卡洛随机采样, 可以估计公式(3)的解为
| $ \langle L({\mathit{\boldsymbol{x}}}, \omega )\rangle = \frac{{T({\mathit{\boldsymbol{x}}}, {\mathit{\boldsymbol{y}}})}}{{p(t)}}\left[ {{\sigma _a}({\mathit{\boldsymbol{y}}}){L_e}({\mathit{\boldsymbol{y}}}, \omega ) + {\sigma _s}({\mathit{\boldsymbol{y}}})\frac{{{f_p}({\mathit{\boldsymbol{y}}}, \omega , \omega ')L({\mathit{\boldsymbol{y}}}, \omega ')}}{{p(\omega ')}}} \right] + \frac{{T({\mathit{\boldsymbol{x}}}, {\mathit{\boldsymbol{z}}})}}{{P(z)}}L({\mathit{\boldsymbol{z}}}, \omega ) $ | (4) |
其中, p(t)表示在介质中沿着光线传播路径采样路径上的y点的概率密度函数(PDF); P(z)是光线能够到达物体表面z点的概率; p(ω′)是在光路径上发生散射事件后, 采样散射光方向的PDF. 根据公式(4), 在基于蒙特卡洛技术的参与介质渲染方法中, 通常由3个重要的过程组成: 一是沿着入射光线采样距离t(即确定y点); 二是给定介质中的任意两点x和y, 确定透射率T(x, y); 三是发生散射时进行散射光线采样(即确定ω′). 这其中, 距离采样最为关键, 其采样的好坏直接影响蒙特卡洛方法的收敛性. 对于均匀介质, 距离的采样相对简单, 一般可以直接获取p(t)(以及P(z))的闭式解: 在独立散射假设前提下, p(t)=σtexp(−σtt). 这种方法也称为Closed-Form Tracking. 对于非均匀介质, p(t)通常没有闭式解. 早期依赖光线步进(ray marching)[16, 17]策略, 一种简单的等间距采样方法, 如图 4左所示. 传统的光线步进方法产生的估计是有偏的[18], 所以在间距设置不合理的情况下可能会产生较大的渲染误差, 例如丢失细节. 目前, 多数无偏估计方法采用基于拒绝采样(rejection sample)的Tracking方法(亦称null-collision方法), 其基本的思想是: 在非均匀介质中填充虚构的介质粒子, 从而使得原始的非均匀介质趋向于均匀. 而这种虚构的粒子只是为了填充, 不产生任何的光照改变, 即: 光线碰到虚构的介质粒子时直接通过, 既不发生吸收也不发生散射, 如图 4右所示.

|
图 4 光线步进(ray marching)方法(左)和Delta Tracking方法(右) |
这方面代表性的工作有:
● Delta Tracking[19, 20]: 通过虚构介质粒子(σn(x))的填充得到均匀的介质, 其浓度(即消光系数σt(x))改变为
● Weighted Tracking[24−27]: Weighted Tracking的出现, 是为了缓解传统的Delta Tracking方法中需要Majorant
● Decomposition Tracking[28]: 这种方法是将非均匀介质分解为均匀介质部分和非均匀的残差部分. 其中, 均匀介质部分可以采用前述的闭式解进行采样得到距离tc, 而残差部分可以采用Delta Tracking采样得到距离tr, 最终的采样距离可用t=min(tc, tr)获取. 在实际运行过程中, 一旦tr超过了tc就马上停止, 这样可以极大地节省运行时间, 提高效率. 此外, Decomposition Tracking可以类似Weighted Delta Tracking引入加权, 只是权重和概率的计算不同;
● Spectral Tracking[28, 29]: 对于消光系数用光谱表示的有色介质, 通常不同谱段发生粒子碰撞事件的概率不同, 所以需要不同谱段单独处理. 但是这样会导致计算量急剧增加. 一种做法是选择一条主谱段进行采样[29], 但是这样会引入偏差; 另一种做法引入Weighted Tracking中加权的思想, 只采样一个谱段, 其他谱段通过加权消除偏差[28].
除了距离采样, 还有一些Tracking方法用于高效的透射率T(x, y)估计. 例如: Residual Ratio Tracking[30]结合Decomposition Tracking的介质分解策略和控制变量法(control variates)[31]进行透射率计算; Jonsson等人[32]结合Ratio Tracking[33]和泊松估计[34]进行透射率计算. 以上Tracking方法的本质是, 将介质中的粒子碰撞事件建模为一个泊松点过程(Poisson point process, PPP)[35]. 当然, 前提条件是介质必须满足独立散射假设.
(2) 密度估计方法
这类方法将传统的光子映射(photon mapping)算法[36, 37]从物体表面间的光线传输拓展到处理参与介质[38]. 这类方法通常需要两个阶段: 第1个阶段, 从光源出发向参与介质中发射光子; 第2阶段, 从视点出发, 对于屏幕上每个像素点所对应的光线进行光子收集和密度估计. 在早期的工作[38−41]中, 光子采用点(point)的形态存储, 而光子收集也是基于点(point)的范围查询. Jarosz等人[42]提出: 这种光子密度估计的方法比较低效, 所以建议在光子密度估计阶段采用光束(beam)进行收集, 如图 5所示. 这样, 单个光束收集过程就包含了多个点查询过程, 有效提高了算法的收敛速度, 提升了密度估计的性能.

|
图 5 传统的点(point)收集和光束(beam)收集的区别[42] |
此外, Jarosze等人[43]还提出了渐进式的光束生成方法, 降低光子图的存储开销, 也在一定程度上支持实时的参与介质渲染. 进一步, Jarosze等人[44]又提出了多种更高效的光子存储和密度估计方法, 并详细讨论了点和光束组合的各种可能性, 如图 6所示. 此后, Křivánek等人[45]在同一个参与介质渲染框架中统一了点、光束和光路径, 提出了UPBP (unifying points, beams and paths)方法. 这里, 点是0维的, 而光束是1维的. 事实上, 任意n维的光子存储形态和n维的密度估计方法都可以用来配对. 如果光子的存储成2维或者3维的结构, 则分别对应光子平面和光子体[46]. 相关工作[47]表明: 光子存储的维度越高, 介质渲染收敛的速度越快. 最近, Deng等人[47]进一步将光子平面推广到光子曲面, 达到了这个方向目前最优的性能.

|
图 6 光子的不同形态和不同密度估计方法的组合[45] |
2 两个基本假设
经典的参与介质渲染方法, 无论是蒙特卡洛方法还是密度估计方法, 都基于两点基本假设: 独立散射假设和局部连续假设. 这是辐射传输方程成立的关键, 也是目前绝大多数Tracking方法能够正确运行的前提. 但事实上, 这两点假设是对自然界中真实介质的近似. 当然, 近似的程度或者合理度随介质的变化和应用的需求而不同. 要想进一步提升参与介质渲染的真实感、扩充现有渲染器所能处理的参与介质类型, 就要打破这两点基本假设, 用更精确的模型描述介质的属性, 用更符合物理客观规律的方式处理介质中光的传播. 本节将详细讨论这两点基本假设.
2.1 独立散射假设这里的独立性主要体现在两个方面.
(1) 组成介质的粒子都是独立同分布的, 其频谱满足高斯白噪(white noise)的特征;
(2) 光线射入介质后, 和每个介质粒子发生的碰撞事件是相互独立的, 和其他碰撞事件不相干.
在这个假设前提下, 我们可以推导出目前介质渲染中广泛使用的体渲染方程, 即公式(3). 然而, 大量的物理、大气、环境等领域的测量数据表明: 介质中微小粒子的分布并非独立, 而是具有某种相干性(correlation). 例如: 在大气领域, 大量数据显示: 入射光线与云层中粒子的碰撞事件概率并不满足前面提到的指数分布, 而是符合某种形式的幂律(power law)分布[48−52]. 原因是: 构成云层的水滴粒子在某些局部区域会堆积在一起, 而在另外一些区域则无分布, 这导致不同的水滴之间存在很强的相关性. 在物理学的核反应领域, 学者们也观察到, 球床反应堆中的粒子聚集和能量传输不满足经典的指数分布[53−56]. 甚至在水文领域和生物学领域, 也有介质粒子相干性的报道[57, 58].
当然, 这种介质粒子分布的不均匀性或者说相干性和前面提到的介质的异质性(heterogeneity)是不同的. 如图 7所示: 经典的介质渲染中所谓的异质性虽然考虑了粒子分布的不均匀性, 但是这种不均匀性只体现在宏观上, 微观上还是假设均匀的. 换句话说, 当介质划分得足够小时, 在细分的局部仍然是均匀的. 因此, 在大多数现有的渲染器中, 不均匀介质可以采用三维体素网络进行存储, 而每个体素内是均匀的, 其值根据粒子浓度确定, 如图 7(b)所示. 这种情况下, 光与介质粒子的碰撞事件依然假设是局部独立. 而相干性则表明: 介质无论划分的多小, 任意局部都依然无法达到均匀, 其不均匀程度由粒子的分布概率确定. 在这种情况下, 光线与介质粒子的碰撞事件就不是独立的. 图 8对比了独立散射和空间相干散射的不同. 如图 8(b)所示: 对于相干散射而言, 当前的粒子碰撞事件受上一次碰撞事件影响. 也就是说, 从当前位置x出发到达下一个碰撞点的概率p(t)和自上次碰撞事件发生后到达x的距离s有关. 这也被称为相干介质的记忆效应[59]. 第3节将详细阐述现有的能够处理相干介质散射的渲染技术.

|
图 7 介质粒子的宏观异质性和微观相干性的区别 |
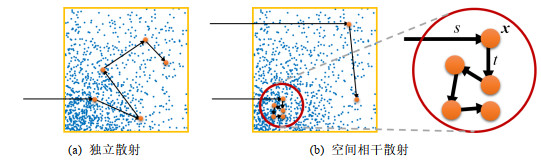
|
图 8 独立散射和空间相干散射 |
2.2 局部连续假设
介质的局部连续性是指介质的相关物理属性(以σt为例)在介质内的任意局部是处处有定义的, 且满足:
| $ {\exists _B}{\forall _{\mathit{\Delta }x < B}}{\sigma _t}(\mathit{\boldsymbol{x}}) = {\sigma _t}(\mathit{\boldsymbol{x}} + \mathit{\Delta} x\mathit{\boldsymbol{r}}) $ | (5) |
其中, r是一个模长为1单位向量, 表示单位球面上的一点. 上述公式表明: 对于介质内的任一点x, 都存在一个半径为B > 0球Br, 使得该球内的每一点的σt都和x点的σt一样大. 这个连续性假设使得现有的渲染器在处理参与介质时, 不需要考虑单个粒子的行为, 只需要考虑大量粒子的统计行为即可. 诚然, 这种假设可以极大地提升参与介质渲染的性能, 但是很难处理离散型介质, 即不满足公式(5)的介质. 这类介质在自然界中广泛存在, 如图 9中的飘雪和浪尖白沫, 还有飞扬的灰尘、堆积的粉末等. 他们通常有两种典型的特征.

|
图 9 自然界中离散介质的案例(左: 飘雪; 右: 浪尖白沫) |
(1) 粒子的大小不一、形态各异, 粒子的大小满足某种分布(如对数正态分布[60]);
(2) 当这类介质离视点很近时, 会表现出明显的颗粒感.
为了捕捉这种颗粒感, 现有的渲染方法通常采用简单几何体(如三维球体)或三角形网格对每个粒子进行显式建模, 然后借助光线追踪等技术估算大量粒子堆积情况下的总体辐射分布[61−63]. 显然, 这种方式会带来巨大的计算资源消耗, 并不利于离散型介质在图形渲染应用中的推广. 第4节将详细阐述目前支持各类离散型介质真实感渲染的方法.
3 相干介质渲染技术迄今为止, 相干介质散射的研究在物理学界也还是一个比较新的前沿课题, 尤其是对空间相干性的研究[64]. 本节主要介绍图形渲染领域所涉及的相干介质散射模型及其渲染方法.
3.1 各向异性介质及其渲染方法在图形渲染领域, 最早探索的介质粒子相干性是有关角度的相干性, 即假设介质散射沿着不同的光线传播方向不同, 消光系数、相函数等辐射量受方向影响. Jakob等人[65]提出了micro-flake模型, 用于建模各项异性的参与介质. 由micro-flake模型推导出的辐射量不仅依赖于位置x, 还依赖于光线在介质中的传播方向ω. 通过引入方向相关性后, 可得到支持各向异性介质的辐射传输方程:
| $ (ω⋅∇)L({\mathit{\boldsymbol{x}}}, ω)=−σ_{a}({\mathit{\boldsymbol{x}}}, ω)L({\mathit{\boldsymbol{x}}}, ω)−σ_{s}({\mathit{\boldsymbol{x}}}, ω)L({\mathit{\boldsymbol{x}}}, ω)+σ_{a}({\mathit{\boldsymbol{x}}}, ω)L_{e}({\mathit{\boldsymbol{x}}}, ω)+σ_{s}({\mathit{\boldsymbol{x}}}, ω)L_{s}({\mathit{\boldsymbol{x}}}, ω) $ | (6) |
该方程同样可以用传统的蒙特卡洛方法进行求解. Heitz等人[66]进一步扩展了micro-flake模型, 引入了针对该模型的对称的GGX分布函数(SGGX), 用于描述micro-flake在三维空间的分布. 该分布函数的优势在于: 能够支持线性插值和预滤波, 满足复杂介质渲染多尺度反走样的需求. 另一个优势是, 可以将介质渲染和表面渲染融合在一个框架中统一处理[67].
3.2 广义线性波尔兹曼方程Larsen和Vasques最早提出了广义线性波尔兹曼方程, 用于建模介质粒子之间的空间相干性[54]. 此后, 该方程成为处理相干介质散射的主流模型之一[68−73]. 2018年, Jarabo等人[74]进一步扩展了该方程, 并将其首次引入图形渲染领域.
广义线性波尔兹曼方程的主要思想是: 在计算参与介质中的自由程概率密度函数p(t)的时候, 将光线已经经过的距离s考虑在内, 如图 8(b)所示. 此时, p(t)不仅和光线出射点x有关, 还和到达x之前光线传播的距离s有关. 为了得到广义线性波尔兹曼方程, 我们首先定义消光系数的微分概率:
| $ \mathit{\Sigma }(t) = \frac{{p(t)}}{{1 - \int_0^t p (s){\rm{d}}s}} $ | (7) |
对于满足独立散射假设的介质而言, p(t)=σtexp(−σtt). 此时, 可以得到Σ(t)=σt, 即传统的消光系数是公式(7)的特例. 当介质不满足独立散射假设时, p(t)不再符合指数分布, 所以Σ(t)≠σt. 将公式(1)中的消光系数σt=σa+σs替换为Σ(t), 并让L(x, ω)也依赖于距离t, 即表示为L(x, ω, t), 可得广义线性波尔兹曼方程(微分形式):
| $ \left. {\begin{array}{*{20}{l}} {\frac{{\rm{d}}}{{{\rm{d}}t}}L(\mathit{\boldsymbol{x}}, \omega , t) + (\omega \cdot \nabla )L(\mathit{\boldsymbol{x}}, \omega , t) = - \mathit{\Sigma } (t)L(\mathit{\boldsymbol{x}}, \omega , t), }\\ {L(\mathit{\boldsymbol{x}}, \omega , 0) = \int_0^\infty {{\mathit{\Sigma }_s}} (t)\int_\mathit{\Omega } L \left( {\mathit{\boldsymbol{x}}, {\omega ^\prime }, t} \right){f_r}\left( {\omega , {\omega ^\prime }} \right){\rm{d}}{\omega ^\prime }{\rm{d}}t + Q(\mathit{\boldsymbol{x}}, \omega )} \end{array}} \right\} $ | (8) |
其中, Σs(t)=αΣ(t)是散射系数的微分概率, Q(x, ω)=σa(x)Le(x, ω)是自发光项. L(x, ω)和L(x, ω, t)的关系为: L(x, ω)=
上述公式的关键是确定和计算p(t). 对于相干介质而言, p(t)通常不满足指数分布, 其形态取决于组成介质的粒子的微观分布情况. 现有的工作通常有两类处理方法: 一类通过蒙特卡洛方法模拟和打表的方式将p(t)预先存储下来[54, 75]; 另一类借助有解析式的经验模型拟合p(t)[76]. 在Jarabo等人的工作中, 采用伽马分布对p(t)进行建模:
| $ p(t) = \frac{{a{C_t}}}{b}{\left( {{C_t}\frac{t}{b} + 1} \right)^{ - (1 + a)}} $ | (9) |
其中, a和b是伽马分布的参数, 和粒子浓度分布的均值和方差相关; Ct表示单个粒子的消光截面. 由上述p(t)可以进一步得到

|
图 10 使用广义线性波尔兹曼方程渲染的各种相干介质(左: 不相干; 中: 正相干; 右: 负相干)[74] |
3.3 支持任意非指数型辐射能量衰减的体渲染方程
相干介质散射最主要的特点是自由程概率密度函数p(t)不再符合指数分布, 所以相应的透射率T(t)也不符合指数分布. 图 11列举了几种不符合指数分布的透射率函数, 通常对应于介质中的粒子分布具有不同的噪声频谱(蓝噪、粉噪以及红噪等). 图 11中的蓝噪频谱对应Jarabo等人工作中的负相干散射, 透射率衰减比指数形式要快; 而粉噪和红噪为正相干散射, 透射率衰减比指数形式要慢. 为了在图形渲染中支持各种不同的非指数型辐射能量衰减, 并保证能量守恒和互易性(reciprocity), Bitterli等人[77]提出一个新的、物理可解释的辐射传输方程.

|
图 11 非指数型透射率函数[77] |
为了保证辐射传输方程能量守恒, 需满足:
| $ 1 = \int_0^z {T({\mathit{\boldsymbol{x}}}, {\mathit{\boldsymbol{y}}}){\sigma _t}({\mathit{\boldsymbol{y}}}){\rm{d}}y} + T({\mathit{\boldsymbol{x}}}, {\mathit{\boldsymbol{z}}}) $ | (10) |
该公式是公式(3)的变体: 删除自发光项, 假设σs=σt, 并假设所有的L等于1. 而上述公式只有在T满足指数分布的情况下才成立. 因此, 当把非指数的透射率函数直接应用到传统的VRE中时, 能量将不守恒. 为了解决这个问题, Bitterli等人提出了传输核(transport kernel)的概念, 定义为
| $ {T_{{\rm{ker }}}}(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{y}}) = \left\{ {\begin{array}{*{20}{l}} {T(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{y}}), }&{{\rm{ if}}\;\mathit{\boldsymbol{y}}\;{\rm{on}}\;{\rm{surface }}}\\ { - \frac{1}{{{\sigma _t}(\mathit{\boldsymbol{y}})}}\frac{\partial }{{\partial t}}T(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{y}}), }&{{\rm{ if}}\;\mathit{\boldsymbol{y}}\;{\rm{in}}\;{\rm{media }}} \end{array}} \right. $ | (11) |
这样的话, VRE(公式(3))中的透射率函数T(x, y)就可以用传输核Tker(x, y)替换, 保证VRE在任意透射率函数下都能能量守恒. 为了进一步支持互易性, Bitterli等人在此基础上又定义了4种不同的传输核, 对应x, y在介质中或者物体表面上的4种组合. 图 12展示了Bitterli等人提出的辐射传输方程所能支持的各种透射率函数及对应的参与介质渲染效果. 值得一提的是: 在不考虑介质边界以及假设介质是宏观均匀的情况下, 上述VRE和Larsen和Vasques提出的广义线性波尔兹曼方程是一致的[54].

|
图 12 不同的透射率函数对参与介质渲染效果的影响[77] |
3.4 支持长程相干性的相干介质渲染方法
相关研究[77, 78]表明, 介质相干散射的形态和介质粒子分布的频谱之间存在一定关系. 因此, 为了获得各种形态的相干介质, 并使其符合物理客观规律, 可以先建模粒子分布的频谱, 再确定相关的辐射量(消光系数、透射率等). 以往的方法中(如Bitterli等人[77]的工作)采用各种形态的噪声(蓝噪、粉噪等)对粒子分布的频谱进行建模, 而这种方式获得的相干性通常只是短程(short range)相干性, 即粒子和粒子之间的相互作用只在有限的局部范围内存在. 为了支持长程(long range)相干性, Guo等人[79]提出采用分数阶高斯随机场(fractional Gaussian fields, FGF)对介质粒子的分布进行建模, 并设计了在FGF描述下的参与介质的渲染方法.
给定一个分数阶的拉普拉斯算子
| $ M = {( - \mathit{\Delta} )^{ - \frac{s}{2}}}W $ | (12) |
其中, W表示一段白噪声. 对该FGF进行傅里叶变换可得:
| $ F[M]=(2π|ν|^{−s})F[W] $ | (13) |
其中, F表示傅里叶算子, ν是d维频率空间的参数. 上式表明: 我们只需要在白噪频谱上乘上一个指数衰减项, 便可以得到各种形态的随机分布和相干性, 而这个衰减项决定了粒子之间的相干性的程度. 我们可以进一步定义Hurst参数H=s−d/2, 这样可以通过调节单个参数H获得不同类型的相干介质. 事实上, 白噪和粉噪是上述表示的特例, 分别对应s=0和H < 0. 当H > 0, 可得到分数阶布朗运动(fractional Brownian motion, fBm), 具有长程相干性. Guo等人提出: 通过将介质的粒子浓度(消光系数分布)建模成FGF, 便可以得到各种类型的相干介质. 图 13展示了不同形态的FGF, 其中, 左图中的红线(H=0)即为短程相干性和长程相干性的分界线. 图 14展示了不同形态的FGF对介质渲染效果的影响. 从图 13、图 14中可以看到: H越大, 粒子越趋向于成团, 从而产生更大范围的相干性, 直至最终形成类似透明的效果. FGF在相干介质模拟中的使用, 极大地丰富了现有的介质渲染所能支持的介质类型, 提升了介质渲染的物理真实感.

|
图 13 不同形态的FGF[79] |

|
图 14 不同的FGF对参与介质渲染效果的影响[79] |
3.5 基于波动光学的相干介质渲染方法
Guo等人[81]最近提出一种基于波动光学的相干介质渲染方法. 该方法从微观物理层面出发, 研究单个粒子的散射行为和大量粒子的堆积方式, 从而推导出宏观层面的辐射物理量(消光系数、相函数等). 传统的方法通常采用米氏散射计算单个粒子的散射行为, 但是米氏散射基于远场(far field)散射假设, 无法处理微观粒子间的近场(near field)相干散射. 为了解决这个问题, Guo等人拓展了米氏散射, 将衍射、干涉等微观粒子间的交互行为引入辐射物理量的计算. 之后, 配合不同的粒子堆积方式获取各种介质渲染效果, 如图 15所示. 值得注意的是, 该方法依然使用传统的辐射传输方程进行介质的渲染.

|
图 15 基于波动光学的介质散射行为模拟[81] |
3.6 对比分析与小结
表 1中列举了上述提到的面向相干介质的渲染方法, 并分别从支持的相干性类型、所依赖的辐射传输方程、所依赖的光学类型以及主要特点进行了对比分析. 从表中可以看出: 早期的工作(如文献[65, 66])主要以介质的角度相干性为主, 而近期的工作更侧重于介质的空间相干性研究. 此外, 现有的工作除文献[81]外都是基于几何光学, 所以理论上, 文献[81]的技术能真实模拟的相干介质类型更广泛. 但是, 目前该方法在渲染的时候还是采用的经典的辐射传输方程. 未来对基于波动光学的辐射传输方程的研究是一个重要的方向.
| 表 1 不同相干介质渲染方法对比分析 |
4 离散介质渲染技术
离散介质在自然界大量存在, 但是图形渲染领域涉及较少, 至今没有一套基于物理的、通用的离散介质渲染方案, 只有针对特定的离散介质(如大颗粒、毛发、纤维等)的高效渲染方法. 经典的辐射传输方程由于基于局部连续性假设, 所以也无法直接应用于渲染离散介质. 本节介绍图形渲染领域现有的能够处理各类离散介质的方法.
4.1 基于预计算的离散颗粒渲染技术图形渲染领域最早进行离散介质渲染尝试的是Moon等人在2007所做的工作[61]. 考虑到对单个粒子进行建模然后采用路径追踪等基于物理的渲染方法进行介质渲染对于离散型介质而言过于耗时, 所以Moon等人提出了壳传输方程(shell transport function, STF)的概念, 用于描述大量离散颗粒聚集情况下, 介质所表现出来的总体的散射分布情况, 如图 16左所示. STF和传统的辐射传输方程不同, 考虑了离散颗粒之间可能存在的相干性. STF定义为Tr(x, ω; y, ω′)=p((y, ω′)|(x, ω)), 该方程给出介质中的某根光束在已知光线沿着(x, ω)到达y的情况下, 从y点沿着ω′方向出射的概率. 有了STF后, 我们就可以回答如下的问题: 在所有沿着(x, ω)传播的光线中, 有多少最终通过y点并沿着ω′继续传播. 这样, 我们就可以通过如下公式计算介质中的任意一点x沿着任意方向ω的辐射率L(x, ω):
| $ L({\mathit{\boldsymbol{x}}}, \omega ) = \int_{{S_r}} {\int_H {{T_r}({\mathit{\boldsymbol{x}}}, \omega ;{\mathit{\boldsymbol{y}}}, \omega ')L({\mathit{\boldsymbol{y}}}, \omega '){\rm{d}}\omega '{\rm{d}}A({\mathit{\boldsymbol{y}}})} } $ | (14) |

|
图 16 壳传输方程和壳追踪[61] |
从而实现壳追踪(shell tracing), 如图 16右所示. 上述公式中, Sr表示半径为r的球面, H表示单位半球面. 壳追踪相比于传统的路径跟踪, 可以极大地降低介质中产生的路径数量, 从而提升大量颗粒渲染的性能.
上述方法的关键是如何获得并计算STF. Moon等人提出采用预计算的方法, 对给定的离散介质进行STF预计算和存储. 每一组STF保存为位置x和球面半径r作为索引的表格. 很显然, 这种预计算方法要求由粒子组成的介质是固定的. 一旦场景改变, 预计算的内容将失效. 为了支持任意场景, 并进一步提升渲染的性能, Meng等人[62]提出了一种多尺度的渲染方法. 该方法的关键是对组成离散介质的单个粒子进行预计算(如图 17所示), 而这些针对单个粒子预计算的内容可以在不同场景间共享. 当已经预计算的粒子通过不同方式进行堆积时, 预计算的内容依旧有效. 此外, 该方法还提出通过显式路径追踪(explicit path tracing, EPT)和体路径追踪(volumetric path tracing, VPT)之间的切换进行高效的渲染, 即: 在靠近视点的物体表面层采用EPT进行处理, 以捕捉介质表层的颗粒感; 远离视点的离散介质内部将离散介质近似为连续介质, 采用连续介质的VPT方法进行处理, 以降低路径采样的数量. 通过这种多尺度渲染的方式, 可以极大地节省渲染的时间开销, 同时保证高质量的细节, 如图 17所示.

|
图 17 Meng等人[62]提出的多尺度离散介质渲染方法 |
之后, Müller等人[63]进一步拓展了上述方法, 提出了针对离散粒子的粒子散射分布函数(grain scattering distribution function, GSDF), 使其支持不同种类粒子的不均匀混合. 对于低阶的散射, 该方法采用GSDF捕捉粒子之间的光能量传输; 而对于高阶的散射, 该方法扩展了STF, 使其支持不均匀的介质粒子混合, 如图 18所示.

|
图 18 Müller等人[63]提出的方法支持非均匀的粒子混合 |
4.2 基于几何光学近似的离散颗粒渲染技术
基于预计算的渲染方法虽然能够支持各种形态的粒子, 但是预计算过程不可避免地带来巨大的计算代价和存储消耗, 所以相关方法很难推广使用. 去除预计算的关键是, 如何快速地计算每个粒子的散射分布函数GSDF. 为了获得精确的结果, 米氏散射[10, 11, 82]被认为是最佳的计算方式. 但是, 米氏散射计算过程非常复杂耗时, 尤其是对于颗粒粒径比较大的情况. Guo等人[83]最近提出采用几何光学近似(geometrical optics approximation)[84, 85]进行快速的单个粒子散射行为分析和计算(图 19(a)). Guo等人通过实验证明: 当颗粒粒径大于一定程度时, GOA的计算结果和米氏散射的计算结果几乎一致, 但是计算的速度快很多. GOA假设光线通过粒子时会发生反射、透射以及衍射, 通过他们之间的能量叠加, 获得最终在单个粒子下的辐射分布. Guo等人提出, 离散介质的颗粒感效果是因为大量不同粒径的粒子在三维空间分布不均匀造成的. 为此, 他们提出了随空间变化的粒子粒径分布函数(spatially-varying particle size distribution, SVPSD)的概念, 如图 19(b)所示. 虽然所有粒子在宏观上满足某种确定的分布, 如对数正态分布[60], 但是在局部, 粒子分布处处不同. 而正是这种分布的差异, 导致视觉上的颗粒感. 借助GOA和SVPSD, Guo等人推导了支持离散介质渲染的通用的多尺度辐射传输方程, 并借助改进的路径追踪方法获得了各种离散介质渲染效果, 如图 19(c)所示. 目前, 该方法只支持球状粒子组成的离散介质.

|
图 19 基于GOA的离散介质散射计算[83] |
4.3 对比分析与小结
表 2中列举了上述提到的面向离散介质的渲染方法, 并分别从所支持的颗粒形状、粒径范围、是否支持非均匀的颗粒组成(异质性)以及预计算和渲染每帧的时间开销进行了对比分析. 这些数据是从每篇文献所提到的渲染场景中归纳总结出来的. 其中, 时间开销分成5档, 点数越多所需的时间也越长. 总体而言, 基于预计算的方法(文献[61−63])的优势是能支持的粒子的形态更丰富, 包括能够支持各种不规则的形体和非均匀分布的颗粒, 但是目前的计算代价偏高; 而基于GOA(文献[83])的方法性能更高, 但是能支持的粒子比较单一. 未来的趋势是将两者的优势结合, 能以较高的性能生成任意形态的离散型介质外观效果.
| 表 2 不同离散介质渲染方法对比分析 |
5 未来展望.
非经典参与介质渲染目前在图形渲染领域还是一个新兴的话题, 尚有很多问题未得到解决, 相关工作也比较零散, 不成体系. 本节展望一下在该方向未来可能的一些发展趋势.
1) 参与介质的相干性和离散性其实在某种程度上是耦合在一起的. 尤其是由大颗粒组成的离散介质(如沙堆、盐堆等), 通常都存在相干散射的情况, 也就是透射率函数不符合指数分布的情况. 目前, 通过预计算的方式可以部分处理这类离散介质中的相干性[61−63]. 但是, 如何在非预计算的离散介质渲染技术(如基于GOA的技术)中引入相干散射的计算还是一个未解的问题. 更一般的情况, 如何将相干性和离散性两种非经典散射情况融合在一个统一的框架中进行高效处理, 是非经典参与介质渲染方法需要解决的一大问题;
2) 现有的大部分非经典参与介质渲染方法(无论是相干介质渲染还是离散介质渲染)都还是在几何光学的框架下进行处理. 尤其是最终都要借助某种形式的辐射传输方程和路径追踪求解. 但是众所周知, 几何光学是对物理光学的近似, 所以很难处理光的干涉、衍射以及偏振等现象. 虽然有一些方法进行了一定的尝试(如Guo等人[81]的工作), 但是, 如何在一个完全基于物理光学的框架下进行非经典介质渲染, 目前还没有合适的方案. 基于物理光学的真实感渲染无论是对于普通的表面还是参与介质, 都可以进一步提升光照效果的物理真实性, 也是渲染领域一个重要的发展方向;
3) 目前, 无论是相干介质渲染还是离散介质渲染都还是面向离线渲染, 无法达到实时的性能. 虽然有些特定的介质, 如织物、毛发等, 通过特定环境下的近似可以达到实时, 但是其介质类型有限, 能适用的场景也不多. 如何将上述提到的各种非经典参与介质渲染方法推广到实时应用中, 是这个领域需要考虑的一个重要的问题, 也将进一步促进非经典参与介质在图形应用中的使用;
4) 随着深度学习的兴起, 参与介质渲染与深度学习技术的结合也成为一个流行的趋势[86−93]. 目前, 有一些参与介质渲染的工作利用了深度学习进行渲染性能的提升. 例如, Kallweit等人[86]提出一种借助深度神经网络进行高效云层渲染的技术, 网络用来学习和表示介质中的辐射度分布. Ge等人[87]通过具有4层的神经网络结构来学习多重散射函数, 从而显著地提升多重散射的模拟速度. Guo等人[91]提出将神经风格化思想引入参与介质的外观建模中, 实现了二维纹理图片到三维反射率体素的风格化迁移, 从而丰富了参与介质的外观效果. 还有一些工作借助神经网络实现了高效的参与介质场景采样[92]和高质量的图片去噪[93]. 当然, 目前这些方法都是针对经典的参与介质渲染的. 如何将深度学习应用于非经典的参与介质渲染方法中, 进一步提升渲染的图片质量并降低渲染所需的时间开销, 也是非经典参与介质渲染领域值得思考的一个方向. 例如, 未来可以研究如何借助神经网络减轻离散颗粒渲染技术中预计算的时间开销, 也可以研究面向相干介质渲染图像的神经网络去噪方法.
6 总结本文从介绍面向经典参与介质的一些常见的渲染方法出发, 阐述了这些方法成立的两点基本假设: 独立散射假设和局部连续假设, 并详细分析了这两点假设所存在的问题. 在此基础上, 本文总结了近年来在图形渲染领域所展开的关于非经典参与介质的渲染方法的研究, 着重阐述了现有的相干介质渲染技术和离散介质渲染技术, 分析他们的原理、优势和不足. 最后展望了该领域未来的研究方向.
| [1] |
Cerezo E, Pérez F, Pueyo X, et al. A survey on participating media rendering techniques. The Visual Computer, 2015, 21(5): 303-328.
|
| [2] |
Novák J, Georgiev I, Hanika J, et al. Monte Carlo methods for volumetric light transport simulation. In: Hildebrandt K, Theobalt C, eds. Proc. of the Eurographics 2018. 2018, 37, Number 2.
|
| [3] |
Wang BB, Fan JH. Survey of rendering methods for homogeneous participating media. Journal of Image and Graphics, 2021, 26(5): 961-969(in Chinese with English abstract).
https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTB202105001.htm |
| [4] |
Fascione L, Hanika J, Heckenberg D, et al. Path tracing in production: Part 1: Modern path tracing. In: Proc. of the ACM SIGGRAPH 2019 Courses (SIGGRAPH 2019). 2019. 19: 1−19: 113.
|
| [5] |
Bauer F. Creating the atmospheric world of red dead redemption 2. In: Proc. of the ACM SIGGRAPH 2019 Course: Advances in Real-Time Rendering in Games. 2019.
|
| [6] |
Bowles H, Cutting TR. Multi-resolution water rendering in crest. In: Proc. of the ACM SIGGRAPH 2019 Course: Advances in Real-Time Rendering in Games. 2019.
|
| [7] |
Chandrasekhar S. Radiative Transfer. Dover, 1960.
|
| [8] |
Henyey LG, Greenstein JL. Diffuse radiation in the galaxy. Astrophysical Journal, 1994, 93: 70-83.
|
| [9] |
Rayleigh JWSL. On the scattering of light by small particles. Philosophical Magazine, 1871, 64: 447-454.
|
| [10] |
Lorenz L. Lysbevægelser i og uden for en af plane Lysbølger belyst Kugle. Det Kongelig Danske Videnskabernes Selskabs Skrifter, 1890: 2−62.
|
| [11] |
Mie G. Beiträge zur optik trüber medien, speziell kolloidaler metallösungen. Annalen der Physik, 1908, 330(3): 377-445.
[doi:10.1002/andp.19083300302] |
| [12] |
Joseph JH, Wiscombe WJ, Weinman JA. The delta-Eddington approximation for radiative flux transfer. Journal of the Atmospheric Sciences, 1976, 33: 2452-2459.
[doi:10.1175/1520-0469(1976)033<2452:TDEAFR>2.0.CO;2] |
| [13] |
Jensen HW, Marschner SR, Levoy M, et al. A practical model for subsurface light transport. In: Proc. of the ACM SIGGRAPH. 2001. 511−518.
|
| [14] |
Donner C, Jensen HW. Light diffusion in multi-layered translucent materials. ACM Trans. on Graphics, 2005, 24(3): 1032-1039.
[doi:10.1145/1073204.1073308] |
| [15] |
Kajiya JT. The rendering equation. Computer Graphics, 1986, 143-150.
|
| [16] |
Tuy HK, Tuy LT. Direct 2-D display of 3-D objects. IEEE Computer Graphics and Applications, 1984, 4(10): 29-34.
[doi:10.1109/MCG.1984.6429333] |
| [17] |
Perlin K, Hoffert EM. Hypertexture. Computer Graphics, 1989, 23(2): 253-262.
|
| [18] |
Raab M, Seibert D, Keller A. Unbiased global illumination with participating media. In: Proc. of the Monte Carlo and Quasi Monte Carlo Methods. 2006. 591−601.
|
| [19] |
Woodcock E, Murphy T, Hemmings P, et al. Techniques used in the GEM code for Monte Carlo neutronics calculations in reactors and other systems of complex geometry. Technical Report ANL-7050. Argonne National Laboratory, 1965.
|
| [20] |
Galtier M, Blanco S, Caliot C, et al. Integral formulation of null-collision Monte Carlo algorithms. Journal of Quantitative Spectroscopy and Radiative Transfer, 2013, 125: 57-68.
[doi:10.1016/j.jqsrt.2013.04.001] |
| [21] |
Yue Y, Iwasaki K, Chen B, et al. Unbiased, adaptive stochastic sampling for rendering inhomogeneous participating media. ACM Trans. on Graphics, 2010, 29(6): 177: 1-177: 8.
|
| [22] |
Yue Y, Iwasaki K, Chen B, et al. Toward optimal space partitioning for unbiased, adaptive free path sampling of inhomogeneous participating media. Computer Graphics Forum, 2011, 30(7): 1911-1919.
[doi:10.1111/j.1467-8659.2011.02049.x] |
| [23] |
Szirmay-Kalos L, Tóth B, Magdics M. Free path sampling in high resolution inhomogeneous participating media. Computer Graphics Forum, 2011, 30(1): 85-97.
[doi:10.1111/j.1467-8659.2010.01831.x] |
| [24] |
Carter LL, Cashwell ED, Taylor WM. Monte Carlo sampling with continuously varying cross sections along flight paths. Nuclear Science and Engineering, 1972, 48(4): 403-411.
[doi:10.13182/NSE72-1] |
| [25] |
Liu M, Ma Y, Guo X. An improved tracking method for particle transport Monte Carlo simulations. Journal of Computational Physics, 2021, 437.
|
| [26] |
Rehak JS, Kerby LM, DeHart MD, et al. Weighted delta-tracking in scattering media. Nuclear Engineering and Design, 2019, 342: 231-239.
[doi:10.1016/j.nucengdes.2018.12.006] |
| [27] |
Morgan LWG, Kotlyar D. Weighted-Delta-Tracking for Monte Carlo particle transport. Annals of Nuclear Energy, 2015, 85: 1184-1188.
[doi:10.1016/j.anucene.2015.07.038] |
| [28] |
Kutz P, Habel R, Li YK, et al. Spectral and decomposition tracking for rendering heterogeneous volumes. ACM Trans. on Graphics, 2017, 36(4).
|
| [29] |
Wilkie A, Nawaz S, Droske M, et al. Hero wavelength spectral sampling. Computer Graphics Forum, 2014, 33(4): 123-131.
[doi:10.1111/cgf.12419] |
| [30] |
Novák J, Selle A, Jarosz W. Residual ratio tracking for estimating attenuation in participating media. ACM Trans. on Graphics, 2014, 33(6): 179: 1-179: 11.
|
| [31] |
Georgiev I, Misso Z, Hachisuka T, et al. Integral formulations of volumetric transmittance. ACM Trans. on Graphics, 2019, 39(6).
|
| [32] |
Jonsson D, Kronander J, Unger J, et al. Direct transmittance estimation in heterogeneous participating media using approximated taylor expansions. IEEE Trans. on Visualization and Computer Graphics, 2020.
|
| [33] |
Cramer SN. Application of the fictitious scattering radiation transport model for deep-penetration Monte Carlo calculations. Nuclear Science and Engineering, 1978, 65(2): 237-253.
[doi:10.13182/NSE78-A27154] |
| [34] |
Kettunen M, d'Eon E, Pantaleoni J, et al. An unbiased ray-marching transmittance estimator. ACM Trans. on Graphics, 2021, 40(4): 137.
|
| [35] |
Cox DR, Lewis PAW. The Statistical Analysis of Series of Events. Wiley, 1966.
|
| [36] |
Jensen HW. Global illumination using photon maps. In: Proc. of the Rendering Techniques'96. 1996. 21−30.
|
| [37] |
Jensen HW. Realistic Image Synthesis using Photon Mapping. Publisher: AK Peters, 2001.
|
| [38] |
Jensen HW, Christensen PH. Efficient simulation of light transport in scenes with participating media using photon maps. In: Proc. of the SIGGRAPH'98. 1998. 311−320.
|
| [39] |
Hachisuka T, Ogaki S, Jensen HW. Progressive photon mapping. In: Proc. of the ACM SIGGRAPH Asia 2008. 2008. 130.
|
| [40] |
Hachisuka T, Jensen HW. Stochastic progressive photon mapping. In: Proc. of the ACM SIGGRAPH Asia 2009. 2009. 141.
|
| [41] |
Knaus C, Zwicker M. Progressive photon mapping: A probabilistic approach. ACM Trans. on Graphics, 2011, 30(3): 25.
|
| [42] |
Jarosz W, Zwicker M, Jensen HW. The beam radiance estimate for volumetric photon mapping. Computer Graphics Forum. 2008, 27(2): 557−566.
|
| [43] |
Jarosz W, Nowrouzezahrai D, Sadeghi I. A comprehensive theory of volumetric radiance estimation using photon points and beams. ACM Trans. on Graphics, 2011, 30(1).
|
| [44] |
Jarosz W, Nowrouzezahrai D, Thomas R, et al. Progressive photon beams. ACM Trans. on Graphics (Proc. of the SIGGRAPH Asia), 2011, 30(6).
|
| [45] |
Křivánek J, Georgiev I, Hachisuka T, et al. Unifying points, beams, and paths in volumetric light transport simulation. ACM Trans. on Graphics, 2014, 33(4): 103: 1-103: 13.
|
| [46] |
Bitterli B, Jarosz W. Beyond points and beams: Higher dimensional photon samples for volumetric light transport. ACM Trans. on Graphics, 2017, 36(4): 1-12.
|
| [47] |
Deng X, Jiao S, Bitterli B, et al. Photon surfaces for robust, unbiased volumetric density estimation. ACM Trans. on Graphics, 2019, 38(4): 46: 1-46: 12.
|
| [48] |
Cahalan RF, Snider JB. Marine stratocumulus structure during FIRE. Remote Sens Environ, 1989, 28: 95-107.
[doi:10.1016/0034-4257(89)90108-9] |
| [49] |
Davis AB, Marshak A, Wiscombe WJ, et al. Scale-invariance of liquid water distributions in marine stratocumulus, Part 1—Spectral properties and stationarity issues. Journal of the Atmospheric Sciences, 1996, 53: 11538-11558.
|
| [50] |
Marshak A, Davis AB, Wiscombe WJ, et al. Scale invariance in liquid water distributions in marine stratocumulus. Part Ⅱ: Multifractal properties and intermittency issues. Journal of the Atmospheric Sciences, 1997, 54: 1423-1444.
|
| [51] |
Pfeilsticker K, Erle F, Funk O, et al. First geometrical pathlengths probability density function derivation of the skylight from spectroscopically highly resolving oxygen A-band observations: 1. Measurement technique, atmospheric observations and model calculations. Journal of Geophysical Research, 1998, 103(D10): 11483-11504.
|
| [52] |
Davis AB, Marshak A. Photon propagation in heterogeneous optical media with spatial correlations: Enhanced mean-free-paths and wider-than-exponential free-path distributions. Journal of Quantitative Spectroscopy and Radiative Transfer, 2004, 84(1): 3-34.
[doi:10.1016/S0022-4073(03)00114-6] |
| [53] |
Levermore CD, Pomraning GC, Sanzo DL, et al. Linear transport theory in a random medium. Journal of Mathematical Physics, 1986, 27(10).
|
| [54] |
Larsen EW, Vasques R. Linear transport theory in a random medium. Journal of Quantitative Spectroscopy and Radiative Transfer, 2011, 112(4).
|
| [55] |
Vasques R, Larsen EW. Non-classical particle transport with angular-dependent path-length distributions. I: Theory. Annals of Nuclear Energy, 2014, 70: 292-300.
|
| [56] |
Camminady T, Frank M, Larsen EW. Nonclassical particle transport in heterogeneous materials. In: Proc. of the Int'l Conf. on Mathematics & Computational Methods Applied to Nuclear Science & Engineering. 2017.
|
| [57] |
Loussot T, Harba R, Jacquet G, et al, An oriented fractal analysis for the characterization of texture: Application to bone radiographs. EUSIPCO Signal Process, 1996, 1: 371−374.
|
| [58] |
Perrin E, Harba R, Berzin-Joseph C, et al. Nth-order fractional Brownian motion and fractional Gaussian noises. IEEE Trans. on Signal Processing, 2001, 49(5): 1049-1059.
|
| [59] |
Kostinski AB. On the extinction of radiation by a homogeneous but spatially correlated random medium. Journal of the Optical Society of America A, 2001, 18(8): 1929-1933.
|
| [60] |
Limpert E, Stahel WA, Abbt M. Log-normal distributions across the science: Keys and clues. BioScience, 2001, 51: 341-351.
|
| [61] |
Moon JT, Walter B, Marschner SR. Rendering discrete random media using precomputed scattering solutions. In: Proc. of the 18th Eurographics Conf. on Rendering Techniques (EGSR 2007). 2007. 231−242.
|
| [62] |
Meng J, Papas M, Habel R, et al. Multi-scale modeling and rendering of granular materials. ACM Trans. on Graphics, 2015, 34(4): 49: 1-49: 13.
|
| [63] |
Müller T, Papas M, Gross M, et al. Efficient rendering of heterogeneous polydisperse granular media. ACM Trans. on Graphics, 2016, 35(6): 168: 1-168: 14.
|
| [64] |
Mishchenko MI. 125 years of radiative transfer: Enduring triumphs and persisting misconceptions. In: Proc. of the AIP Conf., Vol. 1531. 2013. 11.
|
| [65] |
Jakob W, Arbree A, Moon JT, et al. A radiative transfer framework for rendering materials with anisotropic structure. ACM Trans. on Graphics, 2010, 29(4).
|
| [66] |
Heitz E, Dupuy J, Crassin C, et al. The SGGX microflake distribution. ACM Trans. on Graphics, 2015, 34(4): 48: 1-48: 11.
|
| [67] |
Dupuy J, Heitz E, d'Eon E. Additional progress towards the unification of microfacet and microflake theories. In: Proc. of the Eurographics Symp. on Rendering: Experimental Ideas & Implementations (EGSR 2016). 2016. 55−63.
|
| [68] |
Vasques R, Larsen EW. Non-classical transport with angular-dependent path-length distributions. 1: Theory. arXiv: 1309.4817, 2013.
|
| [69] |
Vasques R, Larsen EW. Non-classical transport with angular-dependent path-length distributions. 2: Application to pebble bed reactor cores. arXiv: 1310.1848, 2013.
|
| [70] |
Rukolaine SA. Generalized linear Boltzmann equation, describing non-classical particle transport, and related asymptotic solutions for small mean free paths. Physica A: Statistical Mechanics and its Applications, 2016, 450: 205-216.
|
| [71] |
Larsen EW, Frank M, Camminady T. The equivalence of forward and backward nonclassical particle transport theories. In: Proc. of the M & C 2017. 2017.
|
| [72] |
d'Eon E. A reciprocal formulation of non-exponential radiative transfer. 1: Sketch and motivation. arXiv: 1803.03259, 2018. https://arxiv.org/abs/1803.03259
|
| [73] |
d'Eon E. A reciprocal formulation of non-exponential radiative transfer. 2: Monte Carlo estimation and diffusion approximation. arXiv: 1809.05881, 2018. https://arxiv.org/abs/1809.05881
|
| [74] |
Jarabo A, Aliaga C, Gutierrez D. A radiative transfer framework for spatially-correlated materials. ACM Trans. on Graphics, 2018, 37(4): 83: 1-83: 13.
|
| [75] |
Frank M, Goudon T. On a generalized Boltzmann equation for non-classical particle transport. Kinetic and Related Models, 2010.
|
| [76] |
Davis AB, Marshak A, Gerber H, et al. Horizontal structure of marine boundary layer clouds from centimeter to kilometer scales. Journal of Geophysical Research: Atmospheres, 1999, 104(D6).
|
| [77] |
Bitterli BM, Ravichandran S, Müller T, et al. A radiative transfer framework for non-exponential media. ACM Trans. on Graphics, 2018.
|
| [78] |
Bal G, Jing W. Fluctuation theory for radiative transfer in random media. Journal of Quantitative Spectroscopy and Radiative Transfer, 2011, 112(4): 660-670.
|
| [79] |
Guo J, Chen Y, Hu B, et al. Fractional Gaussian fields for modeling and rendering of spatially-correlated media. ACM Trans. on Graphics, 2019, 38(4): 45.
|
| [80] |
Lodhia A, Sheffield S, Sun X, et al. Fractional Gaussian fields: A survey. Probability Surveys, 2016, 13: 1-56.
|
| [81] |
Guo Y, Jarabo A, Zhao S. Beyond mie theory: Systematic computation of bulk scattering parameters based on microphysical wave optics. ACM Trans. on Graphics, 2021, 40(6): 285.
|
| [82] |
Frisvad JR, Christensen NJ, Jensen HW. Computing the scattering properties of participating media using Lorenz-Mie theory. In: Proc. of the ACM SIGGRAPH 2007. 2007. Article 60.
|
| [83] |
Guo J, Hu B, Chen Y, et al. Rendering discrete participating media with geometrical optics approximation. Computational Visual Media, 2022, 8(3): 425-444.
|
| [84] |
Glantschnig WJ, Chen SH. Light scattering from water droplets in the geometrical optics approximation. Applied Optics, 1981, 20(4): 2499-2509.
|
| [85] |
Ungut A, Grehan G, Gouesbet G. Comparisons between geometrical optics and Lorenz-Mie theory. Applied Optics, 1981, 20(17): 2911-2918.
|
| [86] |
Kallweit S, Müller T, Mcwilliams B, et al. Deep scattering: Rendering atmospheric clouds with radiance-predicting neural networks. ACM Trans. on Graphics, 2017, 36(6): 231.
|
| [87] |
Ge LS, Wang BB, Wang L, et al. Interactive simulation of scattering effects in participating media using a neural network model. IEEE Trans. on Visualization and Computer Graphics, 2021, 27(7): 3123-3134.
|
| [88] |
Vicini D, Koltun V, Jakob W. A learned shape-adaptive subsurface scattering model. ACM Trans. on Graphics, 2019, 38(4): 127.
|
| [89] |
Tewari A, Fried O, Thies J, et al. State of the art on neural rendering. Computer Graphics Forum, 2020, 39(2): 701-727.
|
| [90] |
Zhao YZ, Wang L, Xu YN, et al. State-of-the-art survey on photorealistic rendering of 3D sences based on machine learning. Ruan Jian Xue Bao/Journal of Software, 2022, 33(1): 356-376(in Chinese with English abstract).
[doi:10.13328/j.cnki.jos.006334] |
| [91] |
Guo J, Li M, Zong Z, et al. Volumetric appearance stylization with stylizing kernel prediction network. ACM Trans. on Graphics, 2021, 40(4), Article 162.
|
| [92] |
Müller T, Rousselle F, Novák J, et al. Real-time neural radiance caching for path tracing. ACM Trans. on Graphics, 2021, 40(4), Article 36.
|
| [93] |
Xu Z, Sun Q, Wang L, et al. Unsupervised image reconstruction for gradient-domain volumetric rendering. Computer Graphics Forum, 202, 39: 193−203.
|
| [3] |
王贝贝, 樊家辉. 均匀参与介质的渲染方法研究. 中国图像图形学报, 2021, 26(5): 961-969.
https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTB202105001.htm |
| [90] |
赵烨梓, 王璐, 徐延宁, 等. 基于机器学习的三维场景高度真实感绘制方法综述. 软件学报, 2022, 33(1): 356-376.
[doi:10.13328/j.cnki.jos.006334] |
 2023, Vol. 34
2023, Vol. 34


