2. 北京航空航天大学 未来区块链与隐私计算高精尖创新中心, 北京 100191;
3. 北京航空航天大学 计算机学院, 北京 100191;
4. 北京航空航天大学 人工智能研究院, 北京 100191;
5. 北京航空航天大学 沈元荣誉学院, 北京 100191
2. Beijing Advanced Innovation Center for Future Blockchain and Privacy Computing, Beihang University, Beijing 100191, China;
3. School of Computer Science and Engineering, Beihang University, Beijing 100191, China;
4. Institute of Artificial Intelligence, Beihang University, Beijing 100191, China;
5. Shenyuan Honors College, Beihang University, Beijing 100191, China
近年来, 我国数字经济得到蓬勃发展. 数据作为重要资源, 已成为各类数字化转型应用的核心要素. 然而, 随着大众对数据隐私安全的日益关注, 国内外相继颁布如欧盟《通用数据保护条例》等一系列隐私安全法规, 极大地限制了各机构之间的数据共享与流通. 为了探索如何破除新型“数据孤岛”困境, 数据联邦技术以其“原始数据不出域、数据可用不可见”的隐私安全理念, 正在成为一种近来流行的数据共享新范式[1−3].
数据联邦面向多个数据拥有方的自治数据库, 通过结合安全多方计算等隐私安全技术, 实现在原始数据不出本地前提下的多方联合查询. 在数据联邦系统中, 连接查询是核心的查询操作之一, 有着广泛的应用[4−6]. 例如, 银行可通过与保险公司在双方的用户之中进行等值连接查询得到用户的投保信息, 从而进行反欺诈的判断; 经销商可通过与供货方在价格和预算之间进行θ-连接查询, 得到符合预算的所有货物列表. 目前, 已有数据联邦系统如SMCQL[1], Conclave[2]等借助通用的安全多方计算工具库实现数据联邦的连接查询操作, 以及通过专用隐私集合求交协议进行无环连接-聚合查询的Secure Yannakakis[7]等算法. 然而, 上述方法在解决通用型数据联邦连接查询时还存在着如下两项挑战.
• 联邦连接语义单一. 现有的数据联邦连接查询算法可支持的语义较为单一, 大多数算法仅可支持等值连接查询. 而在真实的数据联邦场景中, 两表之间的连接条件往往更为复杂, 通常为包含大于、小于等比较关系的θ-连接查询. 在此场景下, 现有系统无法直接处理此类复杂连接条件的查询.
• 联邦算法开销高昂. 现有的数据联邦系统通常基于通用型安全多方计算工具库实现, 计算时间和通信开销十分巨大. 例如, 在数据规模为2 000行的表格间做安全连接时, 其运行效率比明文连接低4−5个数量级[2], 难以适用于大规模数据联邦系统.
针对上述挑战, 本文聚焦数据库中支持多种连接条件的𝜃-连接, 研究数据联邦中的θ-连接查询问题, 旨在提出一种支持连接条件多、计算效率高的联邦-连接查询算法. 具体而言, 本文基于秘密共享技术设计了数据联邦中的安全多方基础算子, 可支持安全多方的加法、乘法和比较等操作. 基于这些安全多方基础算子, 本文提出了一个通用的联邦θ-连接算法框架, 该框架对连接条件的类型不作要求, 可支持θ-连接. 在此框架的基础上, 本文还提出可通过对各数据拥有方中的数据进行本地明文的预处理, 从而减少连接查询中的安全多方基础算子运算次数, 进一步对联邦θ-连接查询算法进行优化. 本文的主要贡献如下.
• 针对已有数据联邦算法所支持连接语义单一的挑战, 首先, 本文提出了数据联邦中的θ-连接查询问题. 该问题要求在不泄露各数据拥有方本地数据的前提下, 对各方数据通过多种比较运算进行连接, 得到各方联合的连接查询结果. 其次, 针对数据联邦中的θ-连接查询问题, 通过定义基于秘密共享的安全多方基础算子, 设计了数据联邦中通用的θ-连接查询算法框架. 该框架可灵活地支持大于、等于、小于等各种θ-连接查询.
• 针对现有数据联邦系统中连接算法性能表现的挑战, 本文提出了基于本地明文预处理的算法优化策略. 针对算法执行过程中频繁出现的安全多方基础算子, 提出通过本地预排序方法, 利用本地的有序性减少安全多方基础算子的执行次数, 从而优化联邦θ-连接算法执行效率.
• 在基准数据集TPC-H上, 以时间、通信量为指标, 将本文所提算法与现有数据联邦系统进行对比, 验证了所提算法框架和优化策略的有效性. 实验结果表明, 相比于已有的数据联邦系统, 所提算法可将运行时间与通信开销分别降低61.33%和95.26%.
本文第1节介绍本文的相关工作. 第2节给出联邦θ-连接的形式化定义. 第3节介绍本文所提算法的基础框架. 第4节针对该基础框架提出优化策略. 第5节在标准测试集上验证所提算法的性能. 最后, 在第6节对本文进行总结与展望.
1 相关工作安全多方计算是数据联邦中保护数据隐私安全常用的技术之一, 本节将分别从安全多方计算技术和数据联邦连接查询两个方向回顾与本文相关的研究工作. 具体总结如下.
1.1 安全多方计算技术安全多方计算(secure multi-party computation)的概念起源于姚期智院士在1982年提出的百万富翁问题[8].在该问题中, 两位富翁分别知道自己的财富值, 他们希望在不暴露自身财富值的前提下比较出谁更富有. 换言之, 安全多方计算这一范式旨在两个或多个参与方互不信任的情形下, 以不泄露各自私有输入为前提, 安全地联合计算一个事先约定的目标函数[9]. 该技术在数据确权、云存储和联邦学习等多个领域都有广泛的应用[10−12]. 常用的安全多方计算协议有混淆电路(garbled circuits)[13]和秘密共享(secret sharing)[14]等. 接下来, 对两类协议进行简单介绍.
姚期智院士提出了姚氏混淆电路[8], 该协议基于由不经意传输(oblivious transfer)[15]协议实现的安全门电路. 通过对这些安全门电路进行组合, 混淆电路协议可实现几乎任意一种函数的安全计算. 秘密共享协议最早是由Shamir和Blakley提出[16], 同样是安全多方计算技术中的重要协议. 这一协议的基本思想是: 将一份秘密拆分成多份并分享给多个数据拥有方, 而仅当有超过一定阈值的数据拥有方汇集在一起时才可重建出该秘密. 通过这种思想, 同样可实现安全的加法、乘法等操作, 进而可实现对多种函数的安全计算.
从2012年起, 国内外陆续发布了多个基于混淆电路和秘密共享协议的安全多方计算工具库, 例如基于混淆电路协议的ABY[17]、ObliVM[18]、OblivC[19]以及基于秘密共享协议的Sharemind[20]、SPDZ[21]等. 然而, 尽管这些安全多方计算工具库通用性较强, 可安全地实现多种函数的计算, 但基于混淆电路协议的工具库大多仅能支持两个数据拥有方之间的安全计算, 基于秘密共享协议的Sharemind也仅可支持3个数据拥有方之间的安全计算. 此外, 为了提供通用的计算接口, 这些工具库的计算效率往往并不高. 因此, 对于一些应用场景较广的函数, 如隐私保护集合求交[22]等, 则有研究者提出了专用的安全协议进行加速.
1.2 数据联邦连接查询数据联邦这一概念的原型是20世纪80年代出现的联邦数据库[23, 24]. 联邦数据库概念的提出, 最早是用于公司并购后在多个子公司的自治数据库上进行联合查询, 并未考虑到数据的安全隐私问题. 近年来, 随着多方安全计算工具库的出现与人们隐私保护意识的不断增强, 逐渐有研究者在保持联邦数据库中多方自治的前提上, 进行安全查询处理方面的研究. 2017年, Bater等人提出了SMCQL系统[1], 该系统通过ObliVM工具库将SQL的查询计划解析为混淆电路进行执行, 可以支持在两个数据拥有方上的安全连接等查询操作. SMCQL还设计了查询优化器, 能够在保证数据隐私安全的情况下, 尽可能地减少安全多方计算操作, 从而提高查询效率. 但其实验中展现的性能比明文查询慢几个数据量级, 离落地应用仍有较大差距. 2019年发布的Conclave系统基于OblivC和Sharemind可实现2个或3个数据拥有方之间的安全查询, 并将数据联邦的底层数据库扩展到如Spark等大数据处理引擎上[2]. 系统通过下推明文计算等手段对查询计划进行优化, 从而减少安全多方计算操作的次数, 其性能比SMCQL有一定提升, 但距离实用仍有较大差距. 2021年提出的Senate系统更关注如何提升系统的安全性, 考虑在恶意攻击者模型下进行数据联邦的连接等查询操作[25]. 该系统设计了一种分解混淆电路的方法, 将查询计划生成的大规模混淆电路分解为多个可并行处理的小型电路, 从而提高联邦查询性能. 此外, 还有研究工作构建了解决近似查询问题的系统SAQE[26], 该系统结合安全多方计算技术与差分隐私技术, 尝试平衡性能与查询准确率.
上述工作可支持数据联邦中一般形式的连接查询, 但普遍存在查询效率低的问题. 因此, 有研究者尝试针对某些特殊的连接查询进行优化. 如:
• Bater等人提出的Shrinkwrap系统运用差分隐私技术降低了在两方的安全连接查询中需补充的虚拟元组数量[27].
• 2021年发表的Secure Yannakakis算法则主要聚焦于数据分析领域常见的连接-聚合查询操作[7]. 该方法主要面向无环的连接-聚合查询操作, 结合秘密共享、混淆电路以及隐私保护集合求交3种安全多方计算技术, 并对隐私保护集合求交协议进行了扩展, 将连接-聚合查询算法的时间复杂度降至与输入规模成线性. 其查询处理时间较原有系统降低多个数量级, 有效地提高了查询效率.
• 北京航空航天大学研发的虎符系统则针对数据联邦中的空间连接查询操作进行优化[28]. 该系统通过将空间连接查询拆解为基础的明文和安全算子, 提出了基于范围查询算子的高效求解方案, 与SMCQL和Conclave使用的通用安全多方计算库相比有一定的性能提升. 此外, 虎符系统可支持多达10个数据拥有方之间的空间连接查询, 并可向下兼容多种主流的时空数据库系统.
2 问题描述本节首先介绍数据联邦中的基础概念, 随后给出联邦连接查询的形式化定义.
2.1 预备知识定义1(数据拥有方(data silo)).每个数据拥有方s都持有一个自治的本地关系型数据库Ds, 该数据库中包含了m张关系数据表,
数据拥有方s所持有的每张关系数据表
定义2(数据联邦(data federation)).数据联邦由n个数据拥有方si(1≤i≤n)组成, 记作S={s1, s2, …, sn}. 该数据联邦中, 所有数据拥有方的本地数据库
遵循现有研究中对数据联邦的定义[15, 16], 各数据拥有方所持有的数据表具有相同的模式. 换言之, 每张全局关系数据表Tj(1≤j≤m)中的数据可视作横向分布在各数据拥有方之中, 即
定义3(半诚实模型(semi-honest model)).半诚实模型又被称作“诚实但好奇(honest-but-curious)”模型. 该模型是指协议各参与方会诚实地执行数据联邦发起的查询请求与交互协议, 但会在其执行过程中尝试通过自己获得的中间结果推断其他数据拥有方的数据. 除此之外, 各参与方不会进行其他动作, 也不会恶意地发送虚假信息.
本文安全模型中假设数据联邦中的各数据拥有方均遵循半诚实模型的设定, 即联邦中各个数据拥有方均严格遵守协议步骤执行, 而不会恶意篡改执行中间结果发送虚假信息等. 此外, 本文安全模型将充分考虑到各方串谋的情况, 即某几个参与方间互通信息后, 根据串谋所得信息从而推断出其他参与方的原始数据. 本文将通过协议防范在串谋情况下的原始数据泄露风险, 以提供更高的安全保障. 而用户仅接收查询结果, 不影响安全模型.
本文涉及的主要符号见表 1.
| 表 1 主要符号表 |
2.2 问题定义
定义4(联邦θ-连接查询(federated θ-join query)).给定数据联邦S以及其中的两张全局关系数据表Ta和Tb, 在其中通过连接条件θ(Ta[k1], Tb[k2])进行的θ-连接查询, 可形式化表示为
| $ {T^a} \triangleright { \triangleleft _\theta }{T^b} \equiv \bigcup\nolimits_{i,j \in n} {(T_{{s_i}}^a[{k_1}] \triangleright { \triangleleft _\theta }T_{{s_j}}^b[{k_2}])} $ | (1) |
其中, θ连接条件中的θ符号可以是{≤, < , =, > , ≥}等任意一种比较运算符. 例如, θ条件取 < 时, 即对任意元组
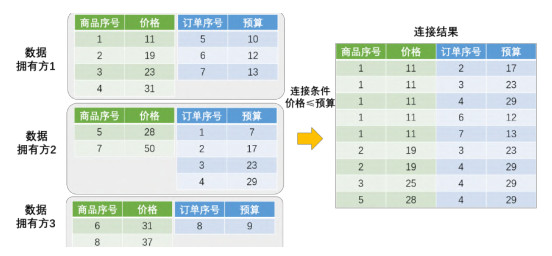
图 1给出了该数据联邦场景下进行θ-连接的一个实例. 在供应链场景下, 供应商有两张表格: 一张是订单表, 记录用户提出的采购需求, 该表有订单序号与预算这两列值; 另一张表格是商品表, 记录供应商的商品信息, 包含商品序号与商品价格这两列信息. 供应商在获悉用户采购需求后, 需要查询所有符合订单预算的候选商品列表, 即商品价格不高于订单预算. 在实际场景中, 可能由多个公司共同提供货品进行联合供应, 此时, 多个供应商构成一个数据联邦. 各数据拥有方持有的数据信息如图 2所示, 每方持有两个表的一部分. 每方不仅需考虑自己持有的商品表与订单表的连接, 还需考虑商品表与其他数据拥有方的商品表进行连接. 如图 2所示, 以数据拥有方1为例, 所持有商品1价格为11, 小于自己已知的订单6、订单7, 且小于数据拥有方2所持有的订单2、订单3与订单4. 因此在最终连接结果中, 商品1与订单2−订单4、订单6、订单7均可连接.
|
图 1 联邦θ-连接实例 |
|
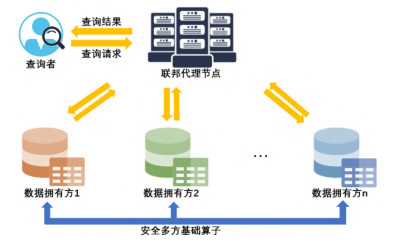
图 2 数据联邦算法框架图 |
3 数据联邦连接查询算法框架
本文采用安全多方计算技术实现数据联邦中的连接查询, 其算法框架如图 2所示. 查询者首先向联邦代理节点发起查询请求, 联邦代理节点解析查询请求并将解析所得子查询分发至各数据拥有方执行. 各方完成子查询后, 由联邦代理节点汇总查询结果并发送结果给用户. 根据以上介绍, 在数据联邦查询整体处理流程中, 联邦代理节点仅承担查询的接收、解析与结果汇总等任务, 仅收集最终结果而不接触各参与方原始数据, 且不参与各数据拥有方间的安全计算, 因此数据联邦的安全性主要在各方联合执行子查询中. 而在子查询执行过程中, 由于θ-连接包含更丰富的语义条件, 因此需要实现支持比较操作的安全多方基础算子, 并基于该算子设计联邦θ-连接处理算法. 考虑到安全操作的计算成本与通信成本较高, 所提算法框架将通过尽可能多的本地明文计算对连接查询算法进行优化, 从而减少安全操作的次数.
本节将分别介绍安全多方基础算子以及基于该算子设计的联邦θ-连接算法框架.
3.1 安全多方基础算子为了保证数据联邦θ-连接查询在执行判断条件时满足安全性约束, 需设计支持比较操作的安全多方基础算子. 本文首先设计并实现了安全多方加法与安全多方乘法这两个基础算子, 然后基于乘法与加法构建安全多方比较算子. 这3个基础算子均基于秘密共享协议, 可通过将各方所持有的秘密进行分发和重建的形式实现安全的多方运算. 数据联邦θ-连接查询则通过调用这些基础算子保证其计算过程的安全性. 本文将所提出的安全多方算子记为poly算子.
• 安全多方加法算子
对于数据联邦中的n个数据拥有方s1, s2, …, sn, 其中, 每个数据拥有方si持有一个数值βi, 安全多方加法算子可在不将任意一个泄露给其他数据拥有方sj(j≠i)的前提下, 计算出
算法1. 安全多方加法算子poly-sum.
Input: 数据拥有方s1, s2, …, sn的数据β1, β2, …, βn.
Output: 各方求和结果β.
1: 随机生成x1, x2, …, xn
2: for数据拥有方si do
3: 随机生成多项Pi(x)=βi+μi1x+μi2x2+…+μin−1xn−1
4: 计算子秘密Pi(xj), 并将其发送给sj(1≤j≤n)
5: for数据拥有方si do
6: 计算秘密
7: 汇总所有σ(xi), 根据公式(2)解得最终结果β
8: return β
具体而言, 该算子将首先随机生成n个互不相同的元素X=x1, x2, …, xn. 随后, 每个数据拥有方si可在本地随机生成一个n−1次多项式
| $ \beta = \sum\limits_{i = 1}^n {\sigma ({x_i})} \prod\limits_{j = 1,j \ne i}^n {\frac{{{x_j}}}{{{x_j} - {x_i}}}} $ | (2) |
• 安全多方乘法算子
对于数据联邦中的两个以秘密形式分布在各方的值[[β1]]=P1(x1), P1(x2), …, P1(xn)和[[β2]]=P2(x1), P2(x2), …, P2(xn), 安全多方乘法算子可在无须知晓β1和β2的前提下计算出β12=β1⋅β2的值. 该算子是对安全多方加法算子的一种拓展, 其伪代码见算法2.
算法2. 安全多方乘法算子poly-multi.
Input: 分布在数据拥有方s1, s2, …, sn的秘密[[β1]]与[[β2]].
Output: 两秘密的乘积β12=β1⋅β2.
1: for数据拥有方si do
2: 计算秘密π(xi)=P1(xi)⋅P2(xi)
3: 汇总所有π(xi), 根据公式(2)解得最终结果β12
4: return β12
在安全多方加法算子中, 数据拥有方si将其收到的秘密相加, 得到新的秘密值σ(xi); 而在安全多方乘法算子中, 则通过将两个秘密相乘的方式得到新的秘密值π(xi). 这一新的秘密值代表了两个多项式P1(x)和P2(x)相乘的结果, π(x)=P1(x)⋅P2(x). 同样地, 可采用与公式(2)类似的方法, 通过多项式插值后将x=0带入的方法得到其常数项, 即为β12. 需要注意的是, 两个多项式P1(x)和P2(x)相乘后, 其最高次项将变为原多项式的2倍. 为了保证可进行多项式插值, 两个秘密[[β1]]和[[β2]]需通过不超过n/2次的多项式进行生成.
• 安全多方比较算子
对于数据联邦中两个数据拥有方sa和sb持有的两个数值βa和βb, 安全多方比较算子可在不泄露βi和βj给对方的前提下, 计算这两个数值的大小关系sign(R): sign(R)=0表示βa=βb; sign(R)=1表示βa > βb; sign(R)=−1表示βa < βb. 该函数sign(R)与R对应关系如式(3)所示.
| $ sign(R) = \left\{ {\begin{array}{*{20}{l}} { - 1,{\text{ }}R < 0} \\ {0,{\text{ }}R = 0} \\ {1,{\text{ }}R > 0} \end{array}} \right. $ | (3) |
该算子需要另外两个数据拥有方st和sk的参与, 其伪代码见算法3.
算法3. 安全多方比较算子poly-cmp.
Input: 数据联邦S, 数据拥有方sa, sb的数据βa, βb.
Output: βa与βb的大小关系R.
1: 随机生成x1, x2, …, xn
2: 数据拥有方sa, sb, st, sk分别随机生成多项式Pa(x), Pb(x), Pt(x)和Pk(x), 并利用此多项式分别生成秘密 [[βa]], [[−βb]], [[pt]]和[[pk]]
3: for数据拥有方si do
4: 计算秘密σa−b(xi)←Pa(xi)+Pb(xi)
5: 计算秘密σt+k(xi)←Pt(xi)+Pk(xi)
6: 调用安全多方乘法算子计算R←[[σa−b]]⋅[[σt+k]]
7: return sign(R)
具体而言, sa和sb分别利用安全多方加法算子中介绍的秘密拆分方法, 将其持有的数值βa和−βb拆分为n个秘密值[[βa]]和[[−βb]]. 数据拥有方st和sk则分别随机生成两个正数pt和pk, 并也采用同样方法将其拆分为n个秘密值[[pt]]和[[pk]]. 随后, 数据拥有方si将其本地所持有的Pa(xi)与P−b(xi)相加得到σa−b(xi), 并将Pt(xi)与Pk(xi)相加得到σt+k(xi). 最后, 秘密[[σa−b]]和[[σt+k]]通过安全多方乘法算子计算得到res=(βa−βb)⋅(pt+pk)的值. 由于pt和pk均为正数, res的正负性与βa−βb的正负性相同. 因此, 通过这种方式即可得出βa和βb的大小关系R.
• 安全多方基础算子复杂度分析
3个安全多方计算基础算子均基于多项式进行秘密分发与重建, 这两个步骤的时间复杂度均为O(n2); 而对安全多方加法算子而言, 各数据拥有方对其本地持有的秘密做运算需要O(n)的时间; 对安全多方乘法和比较算子而言, 由于其仅涉及两个数的相乘和比较, 本地秘密运算仅需O(1)的时间. 因此, 3个安全多方计算基础算子的时间复杂度均为O(n2). 而每个算子均需要n个数据拥有方之间两两进行通信, 且仅需常数次通信即可完成, 故3个安全多方计算基础算子的通信成本也均为O(n2).
• 拓展分析
依据本文所设定的攻击模型中可能存在串谋的情况, 因此在算子设计实现中, 本文算子要求必须全部n个参与方共同参与算子计算, 贡献所持有的秘密共享份额才能完成对秘密值的还原. 然而, 这也带来了较高的通信与计算开销. 因此, 当联邦系统的安全需求降低时, 即系统仅考虑不超过t−1个参与者可能互相串通的情况时, 则安全多方算子需要保证至少t个参与者共同贡献共享份额才能还原秘密值, 以避免任意t−1个参与方串通后即可还原计算的原始数据(t < n). 下面以加法算子poly-sum-(n, t)为例进行介绍, 乘法与比较算子可以此类推. 该算子将首先随机生成t个互不相同的元素X=x1, x2, …, xt; 随后, 每个数据拥有方si可在本地随机生成一个t−1次多项式
由于联邦数据分散在多方, 因此联邦θ-连接实则由多个子θ-连接组成. 而根据联邦组织架构, 子连接查询可分为本地θ-连接与跨成员θ-连接. 由于每张联邦全局视图均横向划分, 散布在多个联邦成员内部, 因此θ-连接查询中涉及的左表与右表也分别由多个数据拥有方持有. 本地θ-连接是指该子查询涉及的左表、右表均在同一个数据拥有方本地; 而跨成员θ-连接是指左表与右表分别在不同数据拥有方中. 本地θ-连接可由数据拥有方在本地明文完成计算, 不涉及隐私安全问题; 而跨成员θ-连接需要保护双方数据隐私, 各方均不希望向对方泄露查询结果外的数据. 因此, 本节主要针对跨成员θ-连接查询的场景, 设计对应的处理算法框架.
θ-连接查询较等值连接查询而言, 内含了更为丰富的连接条件. 联邦场景下, 常通过隐私集合求交协议实现等值连接. 然而隐私集合求交无法满足其他类型的比较运算, 所以在联邦θ-连接查询上, 无法应用高效的隐私集合求交协议. 因此, 本文根据数据联邦上θ-连接查询的特点, 设计了对应的处理算法框架, 主要分为以下3个步骤——比较连接列-确定结果行-拼接结果.
• 比较连接列. 收到基于全局视图的连接查询后, 需要根据各拥有方数据获取其映射关系, 从而将全局查询分解为子查询. 在此, 对解析过程不进行过多介绍, 本文假设已完成查询解析. 两联邦数据拥有方分别持有左表与右表, 并在k1列与k2列上进行θ-连接. 通过调用安全比较算子来比较两列的列值是否符合连接的θ-条件, 可以得知左表与右表的k1列与k2列上分别有哪些值符合连接条件.
• 确定结果行. 根据上一步比较连接列的结果, 符合连接条件的k1列与k2列值会出现在最终连接结果内. 因此需要根据符合条件的k1列与k2列的列值, 找到其在左表与右表中对应的行值, 即对应的元组. 由于筛选出左表与右表中所有符合结果的元组将组成最终的连接结果, 因此不涉及隐私保护需求. 可将元组发送给联邦代理节点进行下一步的拼接操作.
• 拼接结果. 联邦代理节点收到符合连接条件的两表元组后, 根据θ-连接条件, 对相应元组进行复制, 接下来将复制后的左表与右表进行拼接, 即获得最终连接结果.
以上算法框架的伪代码见算法4.
算法4. 联邦θ-连接算法框架.
Input: 数据拥有方s1, s2, …, sn的数据T1, T2, …, Tn与连接列k1, k2以及连接条件θ.
Output: 联邦连接结果R.
1: for数据拥有方si do
2: if si持有
3: 本地计算连接结果并发送至中心
4: for数据拥有方si, sj的
5:
6:
7: 汇总所有方的元组集合, 拼接得到最终结果R
8: return R
算法4描述了联邦连接的算法框架. 第1−3行对应本地连接场景, 每个数据拥有方先判定自己是否同时持有左表与右表的一部分: 若持有, 则先在本地对两表进行连接操作, 并将该结果发送给中心. 第4−7行对应跨成员连接场景. 第4行意为枚举任意两个数据拥有方之间进行子查询. 第5行表明两表按照连接条件进行比较, 此时出于安全需要, 应通过安全多方算子对其进行比较, 以保护各方参与比较的原始数据安全. 并得到符合连接条件的列值集合. 第6行是指根据得到的列值集合, 取出列值在数据表中对应的行值, 得到符合连接条件的元组集合. 第7行中心汇总所有元组值, 并按连接条件拼接出连接结果. 至此得到最终的联邦θ-连接结果.
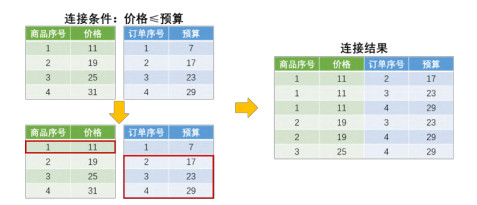
图 3给出了该算法框架的一个实例. 沿用前文提到的实例, 当数据拥有方1与数据拥有方2进行联邦θ-连接时如图 3左上所示, 商品表由数据拥有方1所持有, 订单表由数据拥有方2所持有. 对于商品1, 价格为11. 通过安全多方比较, 可以得知其符合预算为17, 23和29的订单. 通过预算值, 可以找到其对应的订单为序号2−4的订单. 因此, 对于商品(1, 11)元组, 其可以连接的订单元组为(2, 17), (3, 23) (4, 29). 将以上元组发送至中心服务器对其进行拼接, 可得到图 3右侧所示的连接结果中的前3行. 重复该流程, 继续计算商品2~商品4, 即可得到最终全部的连接结果.
|
图 3 联邦θ-连接算法运行实例 |
• 算法安全性分析
算法4的第1−3行均在各数据拥有方本地执行, 不涉及数据拥有方之间的交互, 不会暴露其他信息.第5行涉及数据拥有方si和sj中任意两条数据的安全比较, 其安全性可由安全多方比较算子保证. 在得到比较结果后, 第6行同样仅需本地明文计算. 因此, 算法4可满足本文中安全性的定义, 即在各数据拥有方遵循半诚实模型的前提下, 其无法获知除查询结果外的其他数据拥有方的信息.
• 算法复杂度分析
在算法4中, 第1−3行均为明文计算, 可忽略不计. 第4−6行首先枚举了任意两个数据拥有方si和sj, 第5行分别被对两个数据拥有方中数据表
基于上一节提出的联邦连接泛框架, 其中的核心操作在于如何确定符合连接条件的列值集合. 该操作设计安全保护需求, 需要较高的安全操作开销. 因此, 本节主要针对比较连接列这一环节进行算法设计, 并充分利用比较结果包含的信息, 提出基于排序合并思想的优化策略.
为了实现对两个表的列值比较, 最简单直接的方法是基于双重循环的思想. 然而该方法需要进行O(n2)次的安全比较, 由于安全操作非常耗时, 因此导致此部分成为整个算法的性能瓶颈. 为了减少比较次数, 本文对算法进一步分析. 由于θ-连接中包含的均为比较运算, 而数值的大小关系是一种偏序关系, 具有传递性, 因此可以利用一次比较所得的结果信息减少整体比较次数. 综上, 本文提出了基于Sort-Merge的算法优化策略.
基于以上减少安全操作的优化思想, 本文提出了联邦θ-连接的优化策略. 该策略包含两个阶段, 分别是排序阶段与合并阶段. 其中, 排序阶段可以由各数据拥有方在本地明文执行, 因此该部分不做展开介绍; 而合并阶段主要有列值比较-右指针移动-左指针移动这3个步骤构成.
• 列值比较. 左指针指向左表连接列中的某一列值, 右指针指向右表连接列中的某一列值. 调用安全比较算子, 计算两个列值是否符合θ-连接的条件. 该比较只向双方泄露比较结果, 若符合条件, 则进行左指针移动; 若不符合条件, 则进行右指针的移动.
• 右指针移动. 若比较结果为不符合比较条件, 则指向右表的右指针应当继续向下移动, 以便于继续比较. 此外, 由于列值为有序列表, 因此为找到首个符合要求的列值, 也可以采用二分搜索的方法进行定位.
• 左指针移动. 若比较结果符合条件, 则首先应当将对应列值加入集合中, 然后将左指针下移一位. 根据传递性可知, 左指针所指元素值对右指针前的元素值必然不符合连接条件. 因此, 直接从右指针此时指向的列值继续进行比较即可.
算法5为该优化后联邦连接的算法伪代码.
算法5. 联邦θ-连接优化策略.
Input: 左表
Output: 符合连接条件的列值集合ki, kj.
1: 初始化指针left, right指向首项, ki, kj←∅
2: while left≠end or right≠end do
3: If poly-cmp(L[left], R[right])符合连接条件do
4: Ki, Kj←Ki∪L[left], Kj∪R[right]
5: left←left+1
6: else
7: right←right+1
8: return Ki, Kj
以上伪代码描述了针对列值比较步骤的优化策略. 算法5第1行表示对指针与集合进行初始化, 将指针先指向左右表列值的首项, 将结果集合初始化为空集. 第2−7行描述优化后列值比较的过程: 第3行表示首先通过调用所设计实现的安全多方比较算子poly-cmp, 计算左右指针指向的元素值是否符合连接条件; 第4行、第5行代表若符合连接条件, 则左指针指向值L[left]与右指针指向值及其后续所有右值均符合连接条件, 从而将其加入结果集合, 并且左指针下移一位, 继续进行后续比较; 第6行、第2行表示右指针指向值不符合连接要求, 因此需移动右指针.
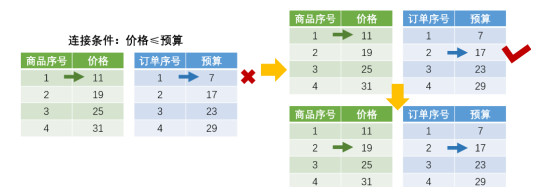
同样沿用前面使用的实例, 通过其中的运行步骤来解释该优化策略. 如图 4所示, 左侧表示算法运行的初始情况, 通过安全算子比较价格列的首项值11与预算列的首项值7, 可知不符合连接的条件. 因此移动右侧指针指向预算列的第2个值, 变为图 4右上所示情况. 再次通过安全比较算子计算可知价格值11与预算值17符合连接条件. 由此可得, 预算17对应的订单2即后续所有订单3、订单4, 均有候选商品1. 完成商品1的比较后, 将左侧指针下移, 继续后续比较. 重复该流程, 即可得到所有符合连接条件的元组.
|
图 4 联邦θ-连接算法优化策略运行实例 |
• 算法安全性分析
在算法5中, 第3行的安全性由安全多方比较算子保证. 对数据拥有方si而言, 在算法5每次仅能得知数据拥有方sj的当前数据是否比L[left]大, 无法得知数据拥有方sj的具体数据. 此外, 可在这一比较过程中得知数据拥有方sj中比L[left]大的数据条数. 但这一信息同样可从连接查询的结果中推断出来, 不会泄露额外的信息. 因此, 基于算法5的数据联邦θ-连接算法同样可保证各数据拥有方在遵循半诚实模型的前提下, 无法获知除查询结果外的其他数据拥有方的信息.
• 算法复杂度分析
算法5是对算法4中第5行的一个优化. 在算法5中, 第2−7行循环次数总共仅为
利用算法5实现的数据联邦θ-连接算法, 仅需
本文通过基准数据集上的实验来衡量本文所提算法相较于已有数据联邦系统的性能提升, 验证本文所提优化策略的有效性. 本节首先介绍实验环境设置, 然后从安全多方算子与联邦θ-连接算法两部分介绍实验.
5.1 实验设置本实验使用多台机器模拟联邦场景下多个数据拥有方的计算模式, 其中每台机器CPU型号为: Intel® Xeon® Platinum 8269CY CPU T 3.10 GHz), 内存32 GB, 操作系统为Ubuntu 18.04.5 LTS (Bionic Beaver), 机器间通信带宽约为6 GB/s. 采用一台机器模拟中心的联邦代理节点, 在其他机器为每个数据拥有方配置对应数据库. 在联邦连接查询执行过程中, 多台机器联合完成计算. 本实验环境设置更好地模拟了各个数据拥有方自治数据的联邦场景.
本实验选择TPC Benchmark™H (TPC-H)作为测试数据集. 该基准数据集是数据库领域测试系统查询分析性能的常用数据集, 因此本文选择该数据集测试所提连接查询算法的性能表现. TPC-H数据集来自供应商应用场景, 包含多种商品信息、订单信息等数据表, 支持生成不同数据规模的数据集.
本实验选择数据联邦系统SMCQL[5]和Conclave[6]作为比较对象. 这两个系统是近年来出现的代表性数据联邦系统, 且在系统架构设计上具有可拓展性, 可以通过修改调用其底层安全库, 以实现对θ-连接的支持. 具体而言, 本文使用SMCQL和Conclave的底层库ObliVM与SPDZ进行基础算子的操作, 通过将多方计算拆解为两两计算, 以实现ObliVM对多方运算的支持. 其中, ObliVM库在数据规模扩展性上略有局限, 因此将其替换为同类库OblivC, 其在请性能上表现更佳. 实验以连接查询算法的运行时间和通信开销作为衡量算法性能的指标. 具体细节与实验表现如以下各节中所示.
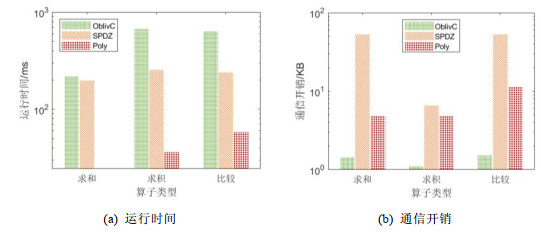
5.2 多方安全算子性能比较首先, 对本文设计实现的3种多方安全算子进行实验验证. 该实验内容为对两个整数进行求和、求积与比较运算. 其中, 比较对象OblivC仅支持两个参与方; SPDZ与本文所提多方安全算子Poly可支持多个参与方的运算, 实验具体设定为4个参与方(如图 5所示).
|
图 5 多方安全算子性能比较 |
从实验结果上可以看出, 本文所提多方安全算子Poly在运行时间上远优于其他方法, 在通信开销上处于中间水准. 在运算时间上, 本文所提方法Poly均耗时最短: 在求和运算上, Poly比SPDZ提升了87.56%; 在求积运算上, Poly比SPDZ提升了85.80%; 在比较运算上, 所提方法比SPDZ提升了75.92%. 这是由于本文方法主要基于秘密共享实现, 比混淆电路耗时更低. 在通信开销上, 本文所提方法均低于SPDZ, 但略高于OblivC: 在求和运算上, 本文所提方法比SPDZ降低了90.82%; 在求积运算上, 本文所提的方法比SPDZ降低了78.46%; 在比较运算上, 本文所提的方法比OblivC降低了78.39%. 由于秘密共享需要参与方间共享秘密值, 因此本文方法在通信开销上略高.
综上实验结果, 本文实现的多方安全算子在运行时间与通信开销上的性能表现良好, 尤其在执行时间效率上优于其他方法, 因此能够有效地支撑在θ-连接中列值比较这一步骤的开销优化. 此外, 本方法在安全协议上考虑多方参与计算, 在安全性上更适用于多方场景.
5.3 联邦θ-连接算法性能比较本文基于多方安全算子构建了包含3阶段的数据联邦连接算法框架, 本节将针对所提算法进行实验验证.本文选择支持θ-连接的数据联邦系统SMCQL与Conclave为比较对象, 然而由于其支持功能有限, 因此本文对其进行了相应的改写拓展. 其中, SMCQL系统在架构设计上支持θ-连接, 然而其作者开源的实现系统仅支持其论文中的3个演示实例, 系统健壮性不足, 因此本文基于SMCQL系统的安全工具库ObliVM实现了θ-连接功能. 然而, 由于ObliVM在数据规模可扩展性上较为局限性, 扩大数据规模后, 其运行时间可达数十个小时[6]. 因此, 为保证实验效果, 将其换为性能表现更好的OblivC. 此外, 两系统对参与方数据量的扩展性都非常有限, 例如, SMCQL系统仅支持两个数据拥有方. 为与所提方法进行对比, 本文也对其系统进行了扩展, 以实现多方的θ-连接.
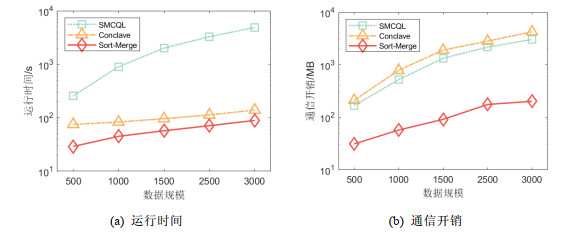
5.3.1 与现有数据联邦系统对比本节实验验证本文所提出的θ-连接查询处理算法的性能表现, 其中, 数据拥有方数量设定为4方. 本文算法与现有联邦系统随数据规模增加的运行时间、通信开销变化如图 6所示.
|
图 6 数据规模变化时, 各系统性能对比 |
从实验比较结果可以看出, 随着查询数据规模的增加, 各算法的运行时间与通信开销均有所增加, 而本文所提的算法均保持性能最佳. 在运行时间上, SMCQL系统运行耗时随数据规模增长出现了明显的增加; Conclave与本文所提Sort-Merge算法的增幅均较为缓慢, 其中, 本文所提Sort-Merge算法耗时在各数据规模下均保持最低, 比SMCQL降低了98.18%, 比Conclave降低了61.33%. 在通信开销上, SMCQL系统与Conclave系统开销相近, 且SMCQL略低于Conclave, 二者开销均随数据规模增加明显增长; 本文所提Sort-Merge算法比二者低一个数量级, 其通信开销比SMCQL降低了93.36%, 比Conclave降低了95.26%. 综合以上实验结果可以看出, 本文所提Sort-Merge算法在数据规模增长时性能表现均优于比较对象SMCQL与Conclave.
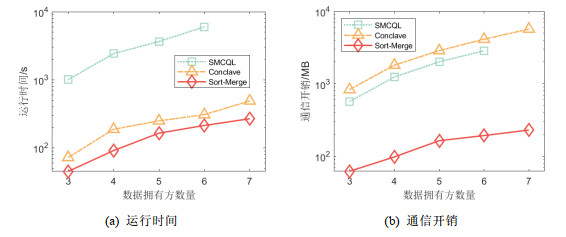
接下来验证本文所提θ-连接查询处理算法在多方场景下的性能表现, 其中, 数据规模设定为1 500行. 本文算法与现有联邦系统随联邦成员数量增加的运行时间、通信开销变化如图 7所示.
|
图 7 数据拥有方数量变化时各系统性能对比 |
从实验比较结果可以看出, 随着数据拥有方数量的增加, 各算法的运行时间与通信开销均有所增加, 而本文所提的算法均保持性能最佳. SMCQL系统的运行耗时随数据拥有方数量的增长出现了明显的增加, 在数据拥有方数量为7方时, 已无法在规定时间内得出结果. 而Conclave与本文所提Sort-Merge算法的增幅均较为缓慢, 其中, 本文所提Sort-Merge算法耗时最低, 比SMCQL降低了95.55%, 比Conclave降低了37.50%. 在通信开销上, 本文所提Sort-Merge算法比SMCQL和Conclave系统低一个数量级, 其通信开销比SMCQL降低了93.23%, 比Conclave降低了95.59%. 综上实验结果可以看出, 本文所提Sort-Merge算法在数据拥有方数量增长时性能表现均优于比较对象SMCQL与Conclave.
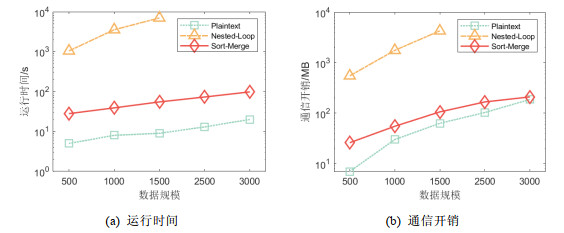
5.3.2 优化策略有效性验证本节实验验证本文所提优化策略Sort-Merge相较于基础算法Nested-Loop的性能提升表现, 其中, 数据拥有方数量设定为4方. 算法随数据规模增加的运行时间、通信开销变化如图 8所示.
|
图 8 数据规模变化时各算法性能对比 |
从实验结果可以看出, 本文所提的优化策略Sort-Merge相较于基础算法Nested-Loop有着较大的性能提升, 其运行时间与通信开销均接近于明文查询. 随着运行数据规模的增加, Nested-Loop方法的连接查询耗时明显增加, 在数据规模为2 600时, 已无法在规定时间内得出结果. Sort-Merge算法在运行数据规模增加时的连接查询耗时增速较慢. 与Nested-Loop算法相比, Sort-Merge算法的运行时间降低两个数量级, 不超过明文查询耗时的5倍. 就通信开销而言, Sort-Merge算法相较于Nested-Loop算法可减少96.10%, 且随着数据规模的增加, Sort-Merge算法的通信开销逐渐逼近明文查询.
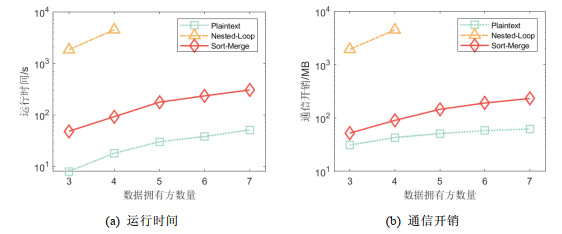
接下来验证本文所提出的算法优化策略在数据拥有方数量变化时的性能提升情况, 其中, 数据规模设定为1 500行. 其运行时间和通信开销如图 9所示.
|
图 9 数据拥有方数量变化时各算法性能对比 |
可以发现, 随着数据拥有方数量的增长, 所有算法的运行时间和通信开销均逐渐增加. 在数据拥有方数量为5时, 基础算法Nested-Loop已无法在规定时间内得出结果. 与其相比, Sort-Merge算法的运行时间与通信开销均下降了一个数量级. Sort-Merge算法的通信开销相较于明文查询而言仅增加了170 M, 这进一步证明了所提优化策略Sort-Merge的有效性.
6 总结与展望本文研究了数据联邦场景下的数据库连接查询问题. 首先, 针对现有研究对连接查询语义支持有限的问题, 本文提出了联邦θ-连接查询, 其可支持大于、小于等更复杂的连接条件. 为了解决这一问题, 本文基于秘密共享技术设计了3个安全多方基础算子. 通过将该算子应用到数据表中的数值比较之中, 本文给出了联邦θ-连接查询算法的基础框架, 并进一步利用各数据拥有方的本地有序性, 将更多的比较运算下推至本地明文执行, 从而进一步优化算法性能. 通过在公开的基准测试集TPC-H上进行实验比较, 验证了所提算法框架和优化策略的有效性. 相比于已有数据联邦系统, 本文所提算法能够将运行时间和通信开销分别降低61.33%和95.26%.
本系统的未来工作如下.
• 支持数据联邦中多表的连接查询算法. 本文所提算法仅可支持数据联邦中分散在多方的两张数据表之间的连接查询, 直接将该方法扩展到多张表的查询则会泄露在连接过程中的中间结果, 存在隐私泄露风险. 如何针对这一场景设计相应算法支持多张表的联邦θ-连接查询, 具有较高的研究价值.
• 面向恶意攻击者模型的连接查询算法. 本文基于半诚实模型假设, 即每个数据拥有方会如实地按照多方协议执行相应的查询, 仅会在协议的执行过程中尝试推断其他数据拥有方的信息, 不会恶意发送错误数据. 而恶意攻击者模型则是指数据拥有方可能不按照协议执行查询, 并发送错误数据, 从而骗取其他数据拥有方的信息. 如何在此模型下设计联邦连接查询算法, 同样是值得研究的问题之一.
| [1] |
Bater J, Elliott G, Eggen C, et al. SMCQL: Secure query processing for private data networks. Proc. of the VLDB Endowment, 2017, 10(6): 673-684.
|
| [2] |
Volgushev N, Schwarzkopf M, Getchell B, et al. Conclave: Secure multi-party computation on big data. In: Proc. of the 14th EuroSys Conf. 2019. 1−18.
|
| [3] |
Li SY, Ji YD, Shi DY, Liao WD, Zhang LP, Tong YX, Xu K. Data federation system for multi-party security. Ruan Jian Xue Bao/ Journal of Software, 2022, 33(3): 1111-1127(in Chinese with English abstract).
http://www.jos.org.cn/1000-9825/6458.htm [doi:10.13328/j.cnki.jos.006458] |
| [4] |
Yang Q, Liu Y, Chen TJ, et al. Federated machine learning: Concept and applications. ACM Trans. on Intelligent Systems and Technology, 2019, 10(2): Article No. 12.
|
| [5] |
Shi YX, Tong YX, Zeng YX, et al. Efficient approximate range aggregation over large-scale spatial data federation. IEEE Trans. on Knowledge and Data Engineering, 2023, 35(1): 418-430.
|
| [6] |
Li T, Sahu AK, Talwalkar A, et al. Federated learning: Challenges, methods, and future directions. IEEE Signal Processing Magazine. 2020, 37(3): 50−60.
|
| [7] |
Wang Y, Yi K. Secure Yannakakis: Join-aggregate queries over private data. In: Proc. of the Int'l Conf. on Management of Data. 2021. 1969−1981.
|
| [8] |
Yao AC. Protocols for secure computations. In: Proc. of the 23rd Annual Symp. on Foundations of Computer Science. IEEE, 1982. 160−164.
|
| [9] |
Evans D, Kolesnikov V, Rosulek M. A pragmatic introduction to secure multi-party computation. Foundations and Trends® in Privacy and Security, 2018, 2(2−3): 70-246.
|
| [10] |
Zhu Y, Yang YT, Sun ZW, Feng DG. Ownership proofs of digital works based on secure multiparty computation. Ruan Jian Xue Bao/Journal of Software, 2006, 17(1): 157-166(in Chinese with English abstract).
http://www.jos.org.cn/1000-9825/17/157.htm [doi:10.1360/jos170157] |
| [11] |
Liu YX, Chen H, Liu YH, Li CP. Privacy-preserving techniques in federated learning. Ruan Jian Xue Bao/Journal of Software, 2022, 33(3): 1057-1092(in Chinese with English abstract).
http://www.jos.org.cn/1000-9825/6446.htm [doi:10.13328/j.cnki.jos.006446] |
| [12] |
Tan ZH, Yang GM, Wang XW, Cheng W, Ning JY. Threshold secret sharing scheme based on multidimensional sphere for cloud storage. Ruan Jian Xue Bao/Journal of Software, 2016, 27(11): 2912-2928(in Chinese with English abstract).
http://www.jos.org.cn/1000-9825/4943.htm [doi:10.13328/j.cnki.jos.004943] |
| [13] |
Bellare M, Hoang VT, Rogaway P. Foundations of garbled circuits. In: Proc. of the ACM Conf. on Computer and Communications Security. 2012. 784−796.
|
| [14] |
Beimel A. Secret-sharing schemes: A survey. In: Proc. of the Int'l Conf. on Coding and Cryptology. Berlin, Heidelberg: Springer, 2011. 11−46.
|
| [15] |
Rabin MO. How to exchange secrets by oblivious transfer. Technical Memo, TR-81, Aiken Computation Laboratory, Harvard University, 1981.
|
| [16] |
Shamir A. How to share a secret. Communications of the ACM, 1979, 22(11): 612-613.
|
| [17] |
Demmler D, Schneider T, Zohner M. ABY—A framework for efficient mixed-protocol secure two-party computation. In: Proc. of the NDSS. 2015.
|
| [18] |
Liu C, Wang XS, Nayak K, et al. Oblivm: A programming framework for secure computation. In: Proc. of the IEEE Symp. on Security and Privacy. IEEE, 2015. 359−376.
|
| [19] |
Zahur S, Evans D. Obliv-C: A language for extensible data-oblivious computation. IACR Cryptology ePrint Archive, 2015: 1153, 2015.
|
| [20] |
Bogdanov D, Laur S, Willemson J. Sharemind: A framework for fast privacy-preserving computations. In: Proc. of the European Symp. on Research in Computer Security. Berlin, Heidelberg: Springer, 2008. 192−206.
|
| [21] |
Keller M. MP-SPDZ: A versatile framework for multi-party computation. In: Proc. of the ACM SIGSAC Conf. on Computer and Communications Security. 2020. 1575−1590.
|
| [22] |
Freedman MJ, Nissim K, Pinkas B. Efficient private matching and set intersection. In: Proc. of the Int'l Conf. on the Theory and Applications of Cryptographic Techniques. Berlin, Heidelberg: Springer, 2004. 1−19.
|
| [23] |
Sheth AP, Larson JA. Federated database systems for managing distributed, heterogeneous, and autonomous databases. ACM Computing Surveys, 1990, 22(3): 183-236.
|
| [24] |
Josifovski V, Schwarz P, Haas L, et al. Garlic: A new flavor of federated query processing for DB2. In: Proc. of the ACM SIGMOD Int'l Conf. on Management of Data. 2002. 524−532.
|
| [25] |
Bater J, Park Y, He X, et al. SAQE: Practical privacy-preserving approximate query processing for data federations. Proc. of the VLDB Endowment, 2019, 13(12): 2691-2705.
|
| [26] |
Poddar R, Kalra S, Yanai A, et al. Senate: A maliciously-secure MPC platform for collaborative analytics. In: Proc. of the 30th USENIX Security Symp. (USENIX Security 2021). 2021. 2129−2146.
|
| [27] |
Bater J, He X, Ehrich W, et al. ShrinkWrap: Efficient SQL query processing in differentially private data federations. Proc. of the VLDB Endowment, 2018, 12(3): 307-320.
|
| [28] |
Tong YX, Pan XC, Zeng YX, et al. Hu-Fu: Efficient and secure spatial queries over data federation. Proc. of the VLDB Endowment, 2022, 15(6): 1159-1172.
|
| [3] |
李书缘, 季与点, 史鼎元, 廖旺冬, 张利鹏, 童咏昕, 许可. 面向多方安全的数据联邦系统. 软件学报, 2022, 33(3): 1111-1127.
http://www.jos.org.cn/1000-9825/6458.htm [doi:10.13328/j.cnki.jos.006458] |
| [10] |
朱岩, 杨永田, 孙中伟, 冯登国. 基于安全多方计算的数字作品所有权证明. 软件学报, 2006, 17(1): 157-166.
http://www.jos.org.cn/1000-9825/17/157.htm [doi:10.1360/jos170157] |
| [11] |
刘艺璇, 陈红, 刘宇涵, 李翠平. 联邦学习中的隐私保护技术. 软件学报, 2022, 33(3): 1057-1092.
http://www.jos.org.cn/1000-9825/6446.htm [doi:10.13328/j.cnki.jos.006446] |
| [12] |
谭振华, 杨广明, 王兴伟, 程维, 宁婧宇. 面向云存储的多维球面门限秘密共享方案. 软件学报, 2016, 27(11): 2912-2928.
http://www.jos.org.cn/1000-9825/4943.htm [doi:10.13328/j.cnki.jos.004943] |
 2023, Vol. 34
2023, Vol. 34


