2. 上海市大数据管理系统工程研究中心(华东师范大学), 上海 200062;
3. 广西可信软件重点实验室(桂林电子科技大学), 广西 桂林 541004
2. Shanghai Engineering Research Center of Big Data Management (East China Normal University), Shanghai 200062, China;
3. Guangxi Key Laboratory of Trusted Software (Guilin University of Electronic Technology), Guilin 541004, China
矩阵计算作为解决数据分析领域问题的有力工具, 具有悠久的发展历史. 最初, 矩阵的出现是用于求解方程组, 其概念最早可追溯到中国汉代时期的《九章算术》, 其中提到了使用数组来表达、求解线性代数方程组, 即类似于线性代数中矩阵求解的思路. 而“矩阵”这一正式专业术语, 最早则是由James Joseph Sylvester在1850年提出[1], 从此广为使用. 当时, 矩阵仅作为一种表示方程组的工具存在, 各式各样的算法通过矩阵变换来求解方程组. 而后, 随着Arthur Cayley提出了抽象矩阵运算[2], 矩阵也逐渐成为独立于方程组的数据分析工具.
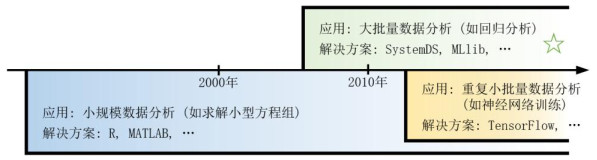
在20世纪末, 矩阵计算已成为数据分析算法中必不可少的一部分. 在诸多企业与科学研究领域, 数据分析师需要为他们的数据自行设计分析算法. 这些算法通常可以通过线性代数符号表示出来, 其中, 数据就成为矩阵, 而数据分析操作就由矩阵计算所组成. 如图 1所示, 为便于数据分析算法的开发, 业内出现了一系列经典的线性代数工具(如R, SAS, MATLAB). 这些工具支持丰富的矩阵计算操作, 能够覆盖几乎所有的数据分析算法需求.
|
图 1 矩阵计算解决方案 |
随着21世纪互联网行业的兴起, 数据的规模和潜在的价值均呈现出爆炸式增长. 为了充分管理、利用大数据, 经济决策、生物医药、图像处理、信息推送等诸多技术领域的大数据分析算法发展迅速, 相关大数据治理应用也逐渐渗透进了社会的方方面面. 由于这些应用需要管理、分析海量数据, 因此往往需要长时间的运行. 其中, 矩阵计算作为数据分析的基础工具, 其效率就成为关键问题[3, 4] (例如, 信息推送中往往需要花费大量时间用支持向量机对数据做特征分类). 然而, 之前的线性代数工具主要关注于功能的全面, 无法扩展到计算机集群上, 难以处理规模大于单节点内存空间的数据集, 因此, 面向大数据分析的分布式矩阵计算系统应运而生.
现如今, 在大数据上支持统计和机器学习算法已成为现代矩阵计算系统的主流要求[5]. 这类系统分为两大类.
● 第1类系统(如TensorFlow[6]、PyTorch[7])面向的是神经网络相关应用, 其特点在于并非批量处理整个数据集, 而是重复采样数据子集.
● 第2类系统(如MADlib[8]、Apache SystemDS[9]、Spark MLlib[10]、Apache Mahout Samsara[11]、LA on SimSQL[12])面向的是批量线性代数工作负载, 其特点是一次性批量处理整个数据集, 一个常见的例子是使用最小二乘法做回归分析.
两类系统所考虑的上层应用和底层的计算框架均有显著的区别, 因此, 本文仅调研其中第2类分布式矩阵计算系统. 这类系统的出现, 让用户不再需要手动处理分布式数据的分配与通信. 通常, 它们会提供一种基于线性代数的语言或嵌入Python, Scala或SQL的接口, 用户通过简单的线性代数符号, 即可操作集群磁盘或内存中的大规模数据. 目前, 分布式矩阵计算系统相关研究技术已日趋成熟, 系统数量众多. 而现有矩阵计算相关综述中更关注于算法而非系统本身[13, 14], 因此, 本文旨在综述系统方向的进展, 为相关研究和用户提供参考.
本文第1节将从数据管理系统的视角分析分布式矩阵计算系统面对的挑战及对应的相关技术. 第2节−第5节分别从编程接口、编译优化、执行引擎、数据存储介绍相关技术. 第6节探讨未来值得关注的研究方向. 第7节总结全文.
1 数据管理视角的分布式矩阵计算系统矩阵计算是一种特殊的数据处理任务, 本文将从数据管理系统的视角来剖析分布式矩阵计算系统. 本节首先从一个矩阵计算应用出发, 介绍分布式矩阵计算系统的相关技术分类.
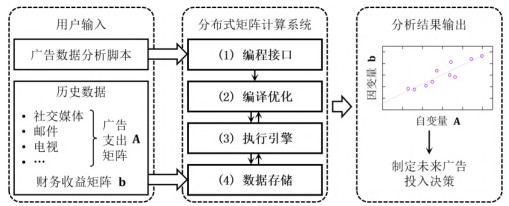
图 2展示了一个利用矩阵计算分析广告数据的应用案例. 在该例中, 用户想要根据历史数据中的广告支出金额与财务收益金额, 构建两者之间的关系, 以服务于未来的广告投入决策. 首先, 用户端需要提供相关历史数据, 并根据系统提供的用户接口编写分析广告数据的脚本; 其次, 分布式矩阵计算系统会按照脚本要求对数据进行处理、分析, 并在最后输出分析结果, 供用户使用. 其中, 系统执行用户脚本的具体流程分为4个部分.
|
图 2 矩阵计算应用的例子 |
(1) 系统通过词法、语法分析将用户脚本编译为便于系统处理的数据结构, 例如语法树, 并基于此生成执行计划.
(2) 为了避免数据分析的时间过长, 系统需要对执行计划进行优化, 例如调整计划中算子的执行顺序.
(3) 由执行引擎具体实施优化后的执行计划.
(4) 在执行引擎实施执行计划的过程中需要不断地访问、组织矩阵数据, 包括用户提供的数据以及脚本中新生成的中间数据.
由此可见, 从数据管理的角度来看, 分布式矩阵计算系统包括编程接口、编译优化、执行引擎、数据存储这4个层面.
值得注意的是, 这4个层面是紧密相关的: 编程接口作为编译优化的上层输入, 其抽象程度决定了优化规则的复杂程度; 编译优化中的决策判断则依赖于底层执行引擎的运行开销和数据存储的方式. 为了能够清晰地梳理、比较, 本文按照系统执行用户脚本的执行流程, 将编程接口、编译优化、执行引擎、数据存储这4个层面的相关技术独立出来, 分别介绍它们所面临的挑战和解决方案.
1.1 研究挑战本节从编程接口、编译优化、执行引擎、数据存储这4个层面分析了分布式矩阵计算系统所面临的挑战.
● 在编程接口层面, 如何权衡编程难度以及表达能力.
影响一套编程接口是否好用的关键因素在于编程难度以及表达能力. 一方面, 编程接口越接近于线性代数表达式, 就意味着编程难度越小, 即用户的开发成本越低. 一个直观的、编程难度低的例子是, 用户可直接向系统提供单机的R语言脚本, 而无须考虑该脚本中的运算逻辑如何扩展到分布式环境下执行. 但是在追求编程难度低的同时, 高度抽象的编程接口会导致用户无法根据一些经验知识对脚本中部分地方的执行进行调整、设置, 也就更依赖系统本身在编译过程中的判断才能保障最终的执行效率. 另一方面, 编程接口要足够灵活, 让用户能够表达自己所需要的计算逻辑或数据组织方式, 但是这往往又会导致编程接口暴露过多关于分布式计算的细节, 用户需要自行了解分布式矩阵计算系统的相关原理, 加大了用户使用的门槛. 由此可见, 分布式矩阵系统的编程接口需要在编程难度以及表达能力这两者之间进行权衡.
● 在编译优化层面, 如何生成最优的执行计划.
编译优化技术对于提升系统性能至关重要. 尤其是在数据分析领域, 算法中往往包含复杂的运算逻辑, 用户难以在编写脚本程序时就采用最佳的执行顺序或方案. 因此, 直接根据该脚本生成的执行计划通常是次优的, 甚至会由于存储空间不足等问题导致系统崩溃. 此时, 系统就依赖于编译优化来解决执行效率问题. 然而, 不同于传统数据库中的查询优化, 复杂的线性代数算法导致生成的执行计划中算子数量多、类型多, 且计划的结构复杂. 因此, 执行计划的潜在优化空间更大, 相关技术也更为关键.
● 在执行引擎层面, 如何根据自身定位选择合适的执行引擎.
如今, 无论在高性能计算、云平台还是数据库等领域, 分布式通用计算框架都已发展成熟. 分布式矩阵计算系统大多无须自行重新设计执行引擎, 而是将已有的通用计算框架作为底层的执行引擎. 然而, 目前通用计算框架种类繁多, 各自的性能表现在不同情况下也截然不同. 故不同定位的分布式矩阵计算系统所需的执行引擎自然也有所不同. 举例来说, 系统需要考虑所面向的硬件环境(如高性能计算框架对硬件要求高)或用户的使用习惯与倾向(如用户工作流中数据存放在数据库中). 因此, 系统需要结合多方面因素来选择最合适的执行引擎.
● 在数据存储层面, 如何设置节省内存占用且提升性能的数据存储方式.
在分布式矩阵计算系统中, 数据存储方式直接决定了数据的内存占用, 同时, 该方式也会影响执行过程中产生的数据传输开销, 因此也间接决定了系统性能的优劣. 除此之外, 在矩阵计算应用中, 需要处理的数据(包括输入数据与中间数据)的特征情况复杂, 例如矩阵的长宽、稀疏度、非零项分布等. 不同特征的矩阵对应的最优存储方式也截然不同, 需要系统能够结合运行时情况自适应地选择合适的数据存储方式.
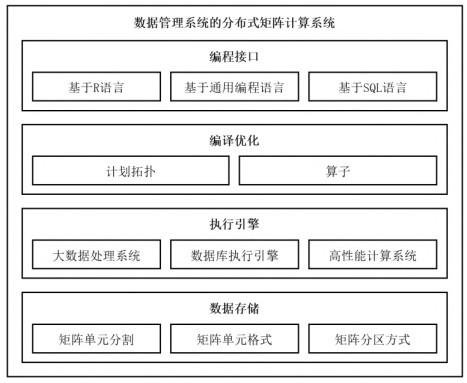
1.2 相关技术分类如图 3所示, 本节从以下4个层面归纳了数据管理视角的分布式矩阵计算系统相关技术.
|
图 3 分布式矩阵计算系统相关技术 |
● 编程接口
数据管理系统已针对接口的编程难度提出了自己的解决方案, 其中最具代表性的包括公认最通用的SQL语言标准以及如JDBC这样的通用编程语言接口. 为了提高接口的表达能力, 不同的数据管理系统各自对SQL进行拓展(如可选择连接操作的实现方式), 供用户灵活调整查询的执行. 类似地, 为了降低编程难度, 分布式矩阵计算系统的编程接口要么是基于数据分析师所熟悉的R语言或SQL语言的, 要么是基于通用编程语言的, 并且同样有系统会通过拓展的方式提供更灵活的接口, 以提高表达能力.
● 编译优化
分布式矩阵计算系统中的编译优化问题可视作数据管理系统中传统查询优化问题的变种, 其解决方案的思路是共通的, 分为优化计划拓扑和优化算子两方面: 首先, 在计划拓扑方面的一个典型例子是多表连接, 数据管理系统需要调整查询计划中连接的顺序以提升执行效率, 类似的问题同样出现在矩阵计算中的矩阵连乘链上; 其次, 在算子方面的一个典型例子是数据管理系统领域中的连接算子, 其实现方式多样, 分别适用于不同的情形, 而在矩阵计算中, 矩阵乘法算子也与其类似, 不同的实现方式各有优劣.
● 执行引擎
根据自身定位的不同, 数据管理系统的执行引擎也具有不同的特点, 例如, 面向分析的系统执行引擎善于处理多谓词的复杂查询, 而面向事务的系统执行引擎则善于处理高并发的数据更新. 对应地, 分布式矩阵计算系统同样有不同的定位, 例如, 面向超级计算机的系统采用的执行引擎是高性能计算系统.
● 数据存储
在数据管理系统中, 往往要对大规模结构化数据进行分布式存储, 其中涉及分割结构化数据、设置分割后数据单元的存储格式以及对数据单元进行分区. 而矩阵就是一种特殊的结构化数据, 对应的相关技术即包括矩阵单元分割、矩阵单元格式和矩阵分区方式.
综上所述, 这4类相关技术分别着眼于解决一批相对独立的分布式矩阵计算系统的问题. 接下来, 本文将就这4项技术分类展开介绍目前的研究进展.
2 编程接口分布式矩阵计算系统的一项重要功能是向上层用户隐藏底层的并行运算逻辑, 降低利用集群资源实现矩阵计算的开发门槛与成本. 为此, 现有的分布式矩阵计算系统提供了一系列编程接口, 根据所依赖的编程语言可分为3类: 基于R语言、基于通用编程语言、基于SQL语言, 图 4分别展示了3种编程语言下的PageRank示例.

|
图 4 PageRank编程示例 |
2.1 基于R语言
基于R语言的编程接口是3类接口中最便捷、使用门槛最低的: 首先, 该类编程接口遵循R语言中原有的数学编程方式, 使得用户能够简单明了地按照数学公式实现算法脚本; 其次, R语言作为一种被广为使用的数学编程语言, 为数据工程师们所熟悉. 当面对要采用分布式矩阵计算的场景时, 用户仅需少量的代码改动(如添加依赖包)即可将原来单机的R语言脚本迁移至分布式环境中运行.
进一步地, 在一系列基于R语言的编程接口中, 存在声明式编程与命令式编程两类.
● 声明式编程[9, 12, 15−18]的特点是惰式计算, 即分布式矩阵计算不会在代码执行后立刻发生, 而是在系统获取完整的算法逻辑后才触发. 例如, 对于一个简单的R语言脚本X=A%*%B; Y=A%*%C(其中, %*%表示矩阵乘法), 分布式矩阵乘法的实际运算发生在第2条语句的执行之后. 这样做的好处在于系统后续可以针对整体算法的执行计划进行查询优化(如调换两处分布式矩阵乘法的顺序), 但是另一方面, 惰式计算也加大了代码的调试难度, 提高了潜在的开发成本.
● 而命令式编程接口[19−23]的特点则是即调即用, 因此相较于声明式编程, 命令式编程的代码调试难度更低, 但同时, 这也阻碍了系统后续的查询优化. 在上述例子中, 分布式矩阵乘法的运算会在第1条语句执行时立刻触发, 此时第2条语句对于系统是不可见的, 这就导致系统只能对每条运算做局部的优化, 最终的运行效率可能不如基于声明式编程的系统.
2.2 基于通用编程语言基于通用编程语言的编程接口允许用户直接在项目工程中运行分布式矩阵计算, 其优势在于灵活, 能够自然地与其他代码逻辑(如数据预处理)整合在一起. 与此同时, 相较于R语言这种最为直接的数学编程方式, 通用编程语言的使用门槛更高, 所以基于这一类编程接口的算法实现成本也更高.
另一方面, 由于通用编程语言的灵活性, 这一系列编程接口对分布式矩阵计算的抽象程度也不尽相同. 其中, SystemDS[24, 25]、DataLog[26]提供了高度抽象的编程接口, 所有分布式相关代码均由系统自动转换生成, 用户无须考虑何时需要调用分布式矩阵计算. 相较于SystemDS、Mahout Samsara、DistArrays[27]、Spartan[28]、MLI[29]、DMac[30]的编程接口的抽象程度较低, 需要用户手动指定哪些矩阵要分布在集群中, 哪些矩阵只需放在单机中, 因此这些编程接口依赖用户对数据规模以及硬件环境有初步的了解, 对用户的要求更高. MLlib更进一步要求用户手动配置各个分布式矩阵的存储形式, 包括RowMatrix、IndexedRowMatrix、CoordinateMatrix与BlockMatrix, 即依赖用户对工作负载以及分布式矩阵计算的运行流程有更深入的理解. SLATE[31]、Chameleon[32]、Elemental[23]的编程接口的抽象程度则更低, 除了矩阵计算的逻辑之外, 用户编写的算法脚本还要负责管理单机与集群间的数据传输. 因此, 基于这些编程接口的代码复杂程度最高, 编程难度最大.
2.3 基于SQL语言SQL是基于关系模型所研发的一套规范语言, 几乎所有主流的数据管理系统和大数据系统均支持SQL[33]. 因为其普及程度之广、影响力之强, 所以亦有系统提供了基于SQL语言的编程接口, 以便于SQL用户调用分布式矩阵计算.
这些编程接口是通过在SQL原有的语法上进行扩展而设计出来的, 其中, 扩展方式分为两类: 一类为SimSQL[12]、MRQL[34]、SciDB[35]、HADAD[36], 直接在SQL上扩展支持矩阵计算操作的语法; 另一类为MADlib, 在SQL上添加自定义函数支持, 用户先使用通用编程语言编写包含矩阵计算逻辑的自定义函数, 随后在SQL脚本中调用该函数. 在这两类编程接口中, 前一类接口与SQL的结合更紧密直接, 但由于受SQL语法结构限制, 仅适合编写简单的算法逻辑; 而后一类接口虽然要求用户额外编写算法脚本, 但受益于通用编程语言, 该类接口能够运用逻辑结构体、Lambda表达式等语法, 以更少的代码实现复杂的算法逻辑.
2.4 小结与分析除了编程语言之外, 表 1还从分布式计算逻辑的透明度、与线性代数的贴合度以及是否采用惰式计算这3个方面分析了前述分布式矩阵计算系统的编程接口, 展示了这些系统之间的共性和差异. 其中, DMac、HADAD为学术原型并未开源, 无法全面了解其编程接口的具体情况, 故未在此列出.
| 表 1 对系统的编程接口的总结 |
● 分布式计算逻辑的透明度
系统用户是否需要在编写脚本时处理分布式计算逻辑, 决定了透明度的高低. 透明度越高, 则表示系统编程接口的封装程度越高, 用户需要考虑分布式计算逻辑的地方越少. 基于此, 现有系统可分为3类. 其中,
➢ 透明度最高的一类系统包括SystemDS、DataLog、SimSQL、MRQL, 它们的编程接口允许用户编写的脚本中不涉及任何关于分布式计算的代码逻辑, 用户可专注于设计算法, 因此, 这类系统的使用门槛最低.
➢ 透明度仅次于此的一类系统包括Presto、pbdR、Mahout Samsara、DistArray、MLI, 它们的编程接口需要用户手动指定哪些矩阵需要进行分布式处理, 但不需要处理具体的分布式计算逻辑. 为此, 用户需要了解脚本中所有矩阵的规模, 根据集群的硬件条件自行判断何处生成分布式矩阵、何时将分布式矩阵转换为本地矩阵. 所以, 这类系统的使用门槛相对更高.
➢ 透明度最低的一类系统包括DPLASMA[17]、SparkR、MadLINQ、Spartan、MLlib、SLATE、Chameleon、Elemental、SciDB, 它们的编程接口要求用户手动管理分布式矩阵的组织方式或计算方式, 因此用户需要充分了解所使用的分布式矩阵计算系统的原理, 才能熟练地编写高效的算法脚本, 使用门槛最高. 但同时, 这类系统的编程接口具有更强的表达能力, 允许用户根据自身的经验知识自定义底层的计算逻辑以提升执行效率.
● 与线性代数的接近程度
最简单、直观地描述数据分析算法的方式就是通过线性代数表达式, 因此, 系统编程接口与线性代数的接近程度直接反映了使用该系统接口的编程难度. 与线性代数接近程度最高的一类系统包括SystemDS、DataLog、Presto、pbdR、Mahout Samsara、SimQL、MRQL, 它们的编程接口主要由线性代数符号组成, 用户所编写的代码即是线性代数表达式. 在接近程度上处于第二梯队的一类系统包括SparkR、MadLINQ、DistArrays、Spartan、MLlib, 它们的编程接口以函数的形式提供了部分线性代数操作, 用户所编写的脚本代码由线性代数符号和函数共同组成. 接近程度最低的一类系统包括DPLASMA、SLATE、Chameleon、Elemental、SciDB, 它们的用户无法直接用线性代数符号来编写脚本, 而需要先编写线性代数表达式, 再利用提供的封装函数编写脚本, 因此, 这类系统接口的编程难度最大, 相较于原线性表达式, 用户脚本的代码量高, 可读性低.
● 惰式计算
为便于优化用户脚本的执行计划, 大多数系统(包括SystemDS、DataLog、Presto、DPLASMA、Mahout Samsara、DistArrays、Spartan、MLlib、SimSQL、MRQL、SciDB)采用了惰式计算.这样可以让系统在得到完整的数据分析逻辑后进行全局的优化, 然而, 惰式计算在脚本有错误的情况下可能无法及时、准确地反映错误代码位置, 因而会加大用户编写脚本时的调试难度.相反地, 也有系统(包括SparkR、pbdR、MadLINQ、SLATE、Chameleon、Elemental)没有采用惰式计算, 牺牲性能以降低调试难度.
3 编译优化矩阵计算广泛应用于机器学习、统计等数据科学领域, 这些领域的应用中往往涉及极其复杂的算法逻辑, 其对应的矩阵计算执行计划也具有复杂的拓扑结构. 因此, 如何做好对计划拓扑的优化, 是提升分布式矩阵计算性能的关键因素. 此外, 不同于单机环境下的矩阵计算, 分布式矩阵计算的性能受制于网络通信的开销.在执行计划中, 不同的算子所引起的网络通信开销有显著不同, 因此, 如何对执行计算中的算子进行优化同样至关重要. 综上, 本节将从计划拓扑与算子这两个层面分析与分布式矩阵计算相关的编译优化技术.
3.1 计划拓扑针对计划拓扑的优化技术可分为两类: 第1类为静态优化技术, 即无须考虑运行时的负载情况, 总是能够提升性能的优化技术; 第2类为动态优化技术, 这类技术在有些运行负载下能够显著提升性能, 但在某些特定情况下也可能造成性能损失, 因此需要结合运行时的负载情况动态制定优化决策.
静态优化技术为一系列通用的表达式替换规则[11, 24], 以简化算法逻辑. 由于无须考虑运行时的负载情况, 系统在构造语法树的过程中即可通过模式匹配的方式触发、应用这些替换规则, 从而优化后续生成的执行计划拓扑. 其中, 替换规则包括:
➢ 常数折叠. 即将多个常数项折叠、计算为单个常数项, 以简化计划拓扑, 例如1+1+A可替换为2+A.
➢ 移除无效操作. 即消除对运算结果无影响的操作, 例如, ATT, 1⋅A, 0+A均可替换为A.
➢ 避免多元操作. 即将包含多个变量的操作简化为包含更少变量的操作, 例如, AA可替换为A2, A−AB可替换为A(1−B).
不同于静态优化技术, 动态优化技术需要根据运行时的负载情况, 在多个计划拓扑间进行权衡, 以提升系统性能. 相关技术如下.
● 增量计算加速
利用增量计算提升系统性能的技术已广泛应用于并行计算系统(如GraphLab[37]、Pregel[38]、Flink/Stratosphere[39, 40]、REX[41]、Naiad[42, 43]), 其核心思想为: 在一个迭代算法中, 如果一轮迭代仅更新了部分的数据(即增量), 那么在下一轮迭代中, 系统可以执行仅与增量相关的操作, 从而避免重复处理没更新的数据. 类似地, 该技术也可应用于矩阵计算. 例如, 对于递归式Xk+1=AXk, 为了应用增量计算加速技术, 系统可将其等价地转换为Xk+1=Xk+A(Xk−Xk−1)=Xk+A⋅ΔXk. 如图 5所示, 当一轮迭代对Xk的更新(即ΔXk)仅覆盖了其部分元素时, 增量计算可显著降低矩阵乘法的计算量.

|
图 5 增量计算 |
然而, 在分布式矩阵计算中盲目地采用增量计算加速技术可能导致对性能提升的收效甚微, 甚至会造成性能降低. 首先, 增量计算中存在雪崩效应. 如图 6所示, 假设Yk=AXkB, 那么当Xk中某一元素发生变化(即ΔXk中仅一个非零项)时, 由ΔYk=A⋅ΔXk⋅B可以得到ΔYk是一个稠密矩阵, 即Xk中一个元素的变化也会导致整个Yk发生变化. 此时, 再在Yk上应用增量计算就不会有性能收益. 为了避免雪崩效应对增量计算性能的影响, LINVIEW[44]、F-IVM[45]提出了基于矩阵分解的增量计算加速技术. 其利用了增量矩阵秩低的特点, 将增量矩阵分解为两个小矩阵的乘积, 以避免增量覆盖范围在矩阵计算过程中逐渐扩大. 在上述例子中, 虽然ΔYk是稠密矩阵, 但实际上, 由ΔYk=A⋅ΔXk⋅B可知, ΔYk的秩与ΔXk的秩一样是1. 为了利用这一点加速矩阵计算, LINVIEW、F-IVM在原增量计算的执行计划上进行了修改. 其先分解ΔXk得到

|
图 6 雪崩效应 |
其次, 增量计算本身存在额外的开销, 尤其在分布式环境下, 增量计算可能远慢于原本的全量计算. 例如在图 5中, 增量计算须维护矩阵旧值Xk−1, 有额外的缓存开销, 而额外的加法则会带来计算与通信开销. 具体来说, 影响增量计算性能的关键因素有两点.
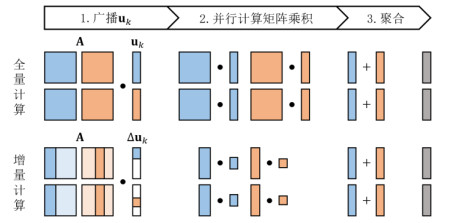
➢ 第一, 增量的非零项往往位置分散, 导致在分布式环境中增量计算无法优化网络通信这一性能瓶颈.以Auk为例, 由于A较大, 系统将其切分为4个部分分布在集群中. 图 7先后展示了全量计算与增量计算的执行过程, 可见, 虽然在广播、计算乘积时增量计算有优势, 但是聚合中间结果时, 全量计算与增量计算的通信开销是相同的, 最终导致增量计算的性能提升效果差. 为了解决这一问题, HyMAC[18]提出了矩阵重组技术, 在分布式矩阵乘法算子前添加重组操作. 该操作会根据分布式矩阵的分区方式尽可能地将增量中的非零项置换到一起, 从而避免增量分散造成的后续影响.
|
图 7 增量分散对分布式矩阵计算过程的影响 |
➢ 第二, 增量矩阵可能是稠密的, 即其中大部分元素均在发生变化, 此时采用增量计算反而会显著地拖慢系统性能.
为此, HyMAC进一步提出了结合全量计算与增量计算的混合计算. 在每轮迭代开始前, HyMAC会动态地基于增量地统计信息进行代价估计, 以判断当前迭代是否采用增量计算.
● 冗余子式消除
矩阵计算应用的算法表达式中可能存在冗余子式, 包括公共子式、循环常量子式. 以Davidon-Fletcher-Powell(DFP)算法解
| $ \begin{array}{*{20}{l}} \boldsymbol{{\rm{while}}}\ loop{{\_}}condition: \hfill \\ \ \ \ \ \begin{aligned} & \boldsymbol{g}_k=\ldots \\ & \boldsymbol{d}_k=\boldsymbol{H}_k \boldsymbol{g}_k \\ & \boldsymbol{H}_{k+1}=\boldsymbol{H}_k+\frac{\boldsymbol{H}_k \boldsymbol{A}^T \boldsymbol{A} \boldsymbol{d}_k \boldsymbol{d}_k^T \boldsymbol{A}^T \boldsymbol{A} \boldsymbol{H}_k}{\boldsymbol{d}_k^T \boldsymbol{A}^T \boldsymbol{A} \boldsymbol{H}_k \boldsymbol{A}^T \boldsymbol{A} \boldsymbol{d}_k}+\frac{\boldsymbol{d}_k \boldsymbol{d}_k^T}{2 \boldsymbol{d}_k^T \boldsymbol{A}^T \boldsymbol{A} \boldsymbol{d}_k} \end{aligned} \end{array} $ |
其中, A, b是输入数据的特征与标签, gk, dk, Hk则分别代表了第k轮迭代的目标函数梯度、搜索方向以及目标函数的海森矩阵. 这里多次出现的Adk就是一个公共子式, 系统可在执行计划中重用Adk的结果[24, 46]; 而由于ATA在循环体中的结果不变, 因此ATA是一个循环常量子式, 系统可在循环体外提前计算ATA而不用每轮迭代都重复计算[46, 47].
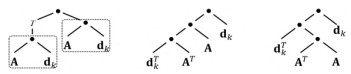
首先, 为了消除冗余子式, 系统需要能够在编译优化阶段感知公共子式与循环常量子式. 一种简单的方法是在生成的执行计划中逐一对算子进行判断, 出现输入、操作均相同的算子则表示存在公共子式, 而出现输入为循环常量的算子则表示存在循环常量子式. 这种方法的缺陷在于, 可能无法找到所有冗余子式. 以
|
图 8 隐式冗余子式 |
为了搜索隐式冗余子式, 就需要不断地对执行计划做等价转换, 而其中面临的最大挑战是线性代数的转换规则过于繁杂. 鉴于此, SPORES[48]提出先将线性代数等价转换为关系代数, 用关系代数中少量的转换规则[49]去生成不同的关系代数计划并搜索冗余, 最终再转换回线性代数计划. 该方法最大的优势在于, SPORES仅需考虑13条关系代数的转换规则, 这13条规则根据语义证明是完备的, 原则上可以发现所有等价的转换情况.然而, 即使仅基于这13条转换规则, SPORES仍面临着一个重大难题, 即远大于标准数据库编译器所能处理的搜索空间. 为此, SPORES采用并扩展了等价饱和[50]的编译技术, 它依赖于一种称为E-Graph的数据结构来表示等价表达式的空间. 在编译优化过程中, SPORES首先使用等价的规则来逐步填充E-Graph, 然后利用约束解算器来从E-Graph中提取性能最佳的表达式. 值得注意的是, 在面对矩阵连乘操作时, 为了避免计划数量爆炸, SPORES采用规则抽样, 并使用贪婪算法来快速覆盖大部分搜索空间, 从而以次优的优化结果换取更短的编译时间.
尽管SPORES能够高效地生成冗余消除方案, 但是在面对矩阵连乘链时仍然会错过部分冗余子式. 为此, ReMac[51]着重针对包含矩阵连乘的算法进行优化. ReMac先按算子优先级将展开后的表达式划分为多个含矩阵连乘或矩阵乘法的块, 随后, 分别在各个块上搜索冗余子式, 最后递归地合并块、重复搜索过程. 其中, 块上的搜索利用了矩阵乘法可结合且不可交换的特性, 通过滑动窗口的方式匹配冗余子式, 以降低搜索空间.
其次, 搜索到的冗余子式之间可能互相冲突, 例如在ATAdk中, 循环常量子式ATA与公共子式Adk是冲突的, 无法在一个同执行计划中消除二者. 甚至有些冗余子式由于改变了原执行计划的拓扑, 反而导致性能下降. 例如: 原执行计划中,
● 算子合并
在矩阵计算中, 多个连续的算子之间存在诸多可进行合并优化的情况, 具体包含3种情况: (1) 避免物化中间结果, 例如, 将(A⊙B)⊙C合并为一个算子, 可避免物化A⊙B的输出(⊙为按位乘操作); (2) 利用稀疏性避免不需要的计算, 例如在A⊙log(BC+ε)中, A是一个稀疏矩阵, 那么实际上, 计算A⊙log(BC+ε)仅需要log(BC+ε)中对应A的非零项的元素即可, 因此将A⊙log(BC+ε)合并为一个算子, 可避免计算log(BC+ε)的全部元素; (3) 充分发挥数据本地性, 例如, AT(Av)可转换为((Av)TA)T, 算子合并后仅需一次按行访问A即可完成计算, 从而避免在两次矩阵乘法算子中重复访问A[52, 53].
根据对算子合并的支持, 现有系统可分为两类: 第1类系统通过固定的模式匹配来寻找可合并优化的算子, 如SystemDS、Mahout Samsara、MATFAST[47]、Cumulon[54], 它们依赖于通过用户手动改写脚本来让系统应用算子合并的技术, 因此, 用户需要投入更高的开发成本才能充分发挥算子合并的优势; 第2类系统则通过重写计划拓扑来自动寻找算子合并的机会, 无须手动改写脚本. 为了自动进行算子合并, BTO[55]、OptiML[56]、Kasen[57]、Tupleware[58]、Weld[59]、TC[60]采用了启发式算法来制定采用算子合并的计划拓扑. 然而, 这些系统没有考虑矩阵稀疏的情况. SPOOF[61]则在此基础上进一步提出了可利用稀疏性避免不需要的计算的算子合并技术, 它们采用的启发式算法不可避免地会错失利用算子合并优化计划拓扑的机会. 为了避免该问题, Boehm等人[62]基于代价估计构建优化问题, 并采用枚举的方式决定算子合并方式, 从而保障了生成的计划拓扑的高效性能.
● 矩阵连乘链优化
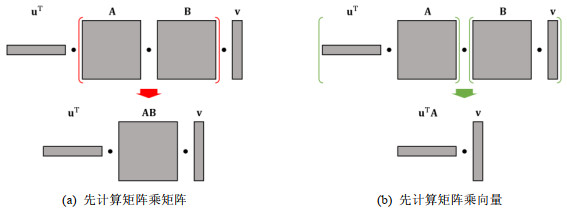
矩阵连乘链的计划拓扑优化问题类似于数据库中的多表连接顺序问题, 不同的矩阵乘法计算顺序会导致显著的性能差异. 以矩阵连乘链uTABv为例, 其中, A, B为方阵. 一种计划拓扑是先计算AB, 如图 9(a)所示.但是在分布式环境中, 两个大矩阵相乘的操作会带来大量的网络通信开销, 因此这种计划拓扑往往是低效的.通常, 系统采用的计划拓扑是优先执行复杂度低、内存占用低的矩阵乘法算子[9, 63], 例如按(uTA)(Bv)的顺序进行计算, 如图 9(b)所示.
|
图 9 矩阵连乘链顺序对性能的影响 |
然而, 随后的计算顺序决策依赖于对中间结果uTA稀疏度的估计, 若uTA比v更稀疏, 则应该先计算(uTA)B; 反之, 则应该先计算Bv. SystemDS采用了基于元数据的稀疏度估计策略, 该策略根据输入矩阵的整体稀疏度估计输出矩阵的整体稀疏度. 这种策略仅依赖输入矩阵的元数据信息(包括行数、列数、非零项个数), 不需要任何采样, 因此几乎没有额外开销. 但是另一方面, 该策略假设非零项是均匀分布在输入矩阵中的, 没有考虑输入矩阵局部稠密、局部稀疏的情况(例如常见的高斯分布), 无法准确地估计矩阵连乘链中间结果的稀疏度, 进而导致计划拓扑可能是次优的. 为了解决这一问题, MNC[64]探寻矩阵连乘链中非零项的分布对稀疏度的影响. 该技术通过低开销的聚合操作获取矩阵的结构信息, 并基于此准确地估计输出矩阵的稀疏度, 从而以可接受的开销换取准确的稀疏度估计以及对矩阵连乘链优化的支持.
● 重编译
上述技术均依赖于运行时的负载信息, 然而在脚本运行前的优化编译阶段, 系统往往无法获取足够的负载信息(例如条件分支、矩阵规模). 为此, SystemDS提出了重编译技术, 即在脚本运行过程中, 重新对计划拓扑进行优化编译. 具体来说, 该技术按照脚本中的逻辑语句将待运行脚本划分为多个部分, 系统在每个部分运行前, 会基于新获取的负载信息对执行计划再次进行优化, 从而进一步改善了编译优化技术提升系统性能的空间.
3.2 算子确定好计划拓扑后, 系统需要进一步对执行计划进行算子层面的优化. 接下来, 本文将从算子实现、算子选择、算子优先级这3个方面介绍相关工作.
● 算子实现
在分布式环境中, 如何高效地实现线性代数算子对系统性能至关重要. 算子主要分为执行聚合操作(如求元素平均值)的算子、执行按位操作(如按位加、按位乘)的算子、执行矩阵乘法操作的算子. 其中, 聚合操作最简单, 分布式系统中已有成熟的聚合技术支持(如allreduce); 类似地, 按位操作的算子实现仅需按行、列位置将两个矩阵中的元素连接起来, 因此可依赖于分布式系统中对连接操作的技术支持(如半连接); 而矩阵乘法算子实现最为复杂, 也往往是性能瓶颈.
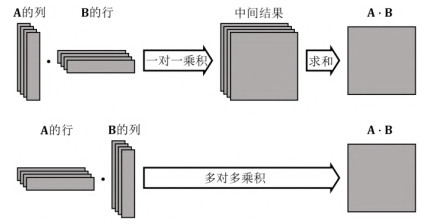
如图 10所示, 分布式矩阵乘法AB的基础实现思路分为两种.
|
图 10 分布式矩阵乘法的实现思路 |
➢ 第1种思路是对A的列与B的行做乘积, 对应的实现为CPMM[65]. CPMM分为3个步骤: (1) 一对一连接A的列与B的行; (2) 计算乘积, 得到中间结果; (3) 对中间结果求和, 得到最终结果.
➢ 第2种思路是对A的行与B的列做乘积, 对应的实现为RMM[65−67]. RMM分为两个步骤: (1) 多对多连接A的行与B的列; (2) 计算乘积, 得到最终结果.
CPMM与RMM有各自适用的情形. 具体来说, CPMM需要在单机内存中缓存中间结果, 并且其并行度依赖于A的列数, 因此不适合A的行数与B的列数相较于A的列数过大的情况; 而RMM在第1步中需要复制A的行与B的列以完成多对多连接, 因此数据传输量更高, 不适合A的列数过大的情况.
针对RMM中需要大量复制矩阵的问题, SystemDS进一步提出了BMM[9], 其将多对多连接的实现改为了广播A, B中较小的矩阵, 尤其在矩阵乘向量的算子上, BMM能够显著地提升系统性能. 但是该实现要求A, B中有一个矩阵足够小, 能够缓存在单机内存中. 在不提高内存要求的前提下, Marlin[68]在RMM的基础上进行了拓展, 通过提高并行度的方式以取得更高的性能. 该实现对RMM中的多对多连接进行了更细致的划分, 并不一次性完成一整行与一整列的连接, 而是将一整行和一整列划分为多个部分, 先连接这些部分, 此处的连接并行度更高, 随后将连接得到的中间乘积结果再做一次求和得到最终结果. 这种做法以更高的传输数据量换取更高的并行度, 适用于网络带宽充足的硬件环境.
● 算子选择.
既然上述这些算子实现有不同的硬件要求以及性能, 那么系统自然需要根据实际情况对这些算子实现进行选择.
首先, 在分布式环境中, 性能瓶颈往往在于网络通信开销, 没有网络通信的单机实现可能要比分布式实现更快, 因此系统需要在分布式与单机之间做选择. 一种简单、通用的判断方式是将向量操作放在单机上完成[10]. SystemDS则进一步提出了基于内存占用估计的判断方式, 即对算子输入、输出和中间结果的内存占用进行估计, 当单机可用内存充足时就选择单机实现, 以避免网络通信. 此外, SystemDS会根据矩阵当前的数据位置进行判断, 若矩阵数据已分布在集群中, 那么在该矩阵上的聚合操作就会采用分布式实现, 而非传输到单机上再做聚合. 由此, SystemDS在充分发挥集群计算能力的同时, 也能进一步减少不必要的网络通信.
其次, 在分布式算子实现上还需要进行选择: 一方面, 这些算子在不同数据规模、硬件条件下的表现各不相同, SystemDS、Mahout Samsara对此构建了代价模型, 逐一选择计划拓扑中的算子实现; 另一方面, 算子与算子的实现之间会互相影响. 尤其在分布式矩阵乘法中, 不同的算子适合不同的输入形式. 例如, 对于AB算子, CPMM适合按列组织A、按行组织B, 而RMM则适合按行组织A、按列组织B. 此外, 输出形式也与算子有关, 例如在AB中, 若较大的矩阵A是按行组织的, 那么BMM的输出也会是按行组织的. 为此, DMac, MATFAST, Spartan根据矩阵连乘链中算子间输入输出的依赖关系对矩阵乘法算子的实现进行选择, 以尽可能地让输入矩阵的形式符合算子实现的需求, 从而提高系统性能.
● 算子优先级.
在计划拓扑中, 往往会存在多条并行的执行路径. 因此在确定计划拓扑后, 还需确定算子优先级, 才能最终生成明确的执行计划. 其中, 最为重要的是明确计划拓扑中的关键路径, 系统需要优先执行关键路径上的算子, 以提高整体的硬件利用率. SLATE、Chameleon、DPLASMA、COnfLUX/COnfCHUX[69]着重针对矩阵分解算法中的算子优先级进行优化, 它们观察到, 在常用的分解算法中, 一个算子的部分输出会作为下一个算子的输出, 而其余部分则不会参与后续计算, 因此这些系统对某些算子的并行实例设置高优先级, 以此提高在关键路径上的运行效率. 例如在Cholesky分解中, 每一轮迭代结果中, 后几列的子矩阵会用于下一轮迭代, 所以在这些子矩阵上的并行实例的优先级就会高于其他并行实例.
3.3 小结与分析表 2从针对计划拓扑或算子的优化、技术通用性、提升计算或传输效率这3个角度分析了前述分布式矩阵计算系统的编译优化技术, 展示了这些系统之间的共性和差异.
| 表 2 对系统的编译优化的总结 |
● 针对计划拓扑或算子的优化
由于数据分析算法的逻辑复杂, 且分布式计算的执行方式也多种多样, 因此, 分布式矩阵计算系统的编译优化技术种类繁多. 总体来说, SystemDS、Mahout Samsara、MATFAST考虑了计划拓扑与算子两方面的优化, 因此, 采用的优化技术较为完备, 充分发挥了编译优化器的作用. 其余的系统则专门针对计划拓扑(包括LINVIEW、F-IVM、HyMAC、SPORES、ReMac、Cumulon、OptiML、BTO、Kasen、Tupleware、Weld、TC、SPOOF)或算子(包括Marlin、DMac、Spartan、SLATE、Chameleon、DPLASMA、COnfLUX/COnfCHUX)进行优化, 相对于前者, 采用的编译优化技术仅局限在某一方面. 以Marlin为例, 尽管其针对矩阵乘法算子进行了优化, 但是若要充分发挥这一优化技术的作用, 也依赖于系统能够在计划拓扑层面结合新的算子实现的开销进行对应的调整.
● 技术通用性
在上述系统中, SystemDS与Mahout Samsara采用的编译优化技术覆盖了多种多样的线性代数表达式的形式, 并不针对某种特定的数据分析算法, 因此编译优化技术通用, 可应用于几乎所有的数据分析算法. 通用性次之的系统则针对某些表达式形式进行优化. 具体来说, MATFAST、Cumulon、OptiML、BTO、Kasen、Tupleware、Weld、TC、SPOOF所采用的算子合并技术仅可优化多种固定的表达式, 而Marlin所提出的矩阵乘法算子实现仅可应用于需要计算两个大规模矩阵的乘积的情况. 最后一类系统的编译优化技术通用性则最低, 专门针对某一类算法进行编译优化. 其中, LINVIEW、F-IVM、HyMAC提出的增量计算优化技术仅针对迭代收敛的算法, SPORES与ReMac局限在一类存在冗余表达式的算法; DMac、Spartan则着眼于由大规模矩阵组成的连乘链, 往往仅局限在矩阵分解算法上; 类似地, SLATE、Chameleon、DPLASMA、COnfLUX/COnfCHUX所提出的算子优先级优化技术, 也专门用于优化矩阵分解算法的执行效率.
● 提高计算或传输效率
在分布式矩阵计算中, 计算复杂度往往很高; 同时, 盲目地进行分布式计算又会产生大量的数据传输开销, 因此, 大多数系统(包括SystemDS、Mahout Samsara、LINVIEW、F-IVM、HyMAC、SPORES、ReMac)采用的编译优化技术以提高计算与传输效率为目标. 当然, 在不同的算法和硬件环境上, 系统的性能瓶颈也有所不同, 由此对应地也出现了不同侧重的系统编译优化技术. 其中, MATFAST、Cumulon、OptiML、BTO、Kasen、Tupleware、Weld、TC、SPOOF、DMac、Spartan着重解决数据传输开销过大的问题; 而SLATE、Chameleon、DPLASMA、COnfLUX/COnfCHUX则致力于调整算子优先级, 以避免计算资源空闲, 从而提高计算效率; Marlin所考虑的情形更为极端, 即计算开销显著高于传输开销, 因此需要通过牺牲传输效率的方式换取更高的计算效率, 以在整体上提升系统性能.
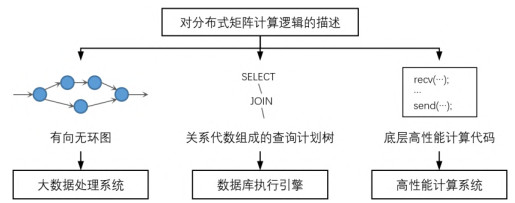
4 执行引擎在编译优化之后, 分布式矩阵计算系统依托于底层的执行引擎以完成最终的分布式计算. 而由于执行引擎的不同, 矩阵计算系统生成的执行计划形式也有所不同. 如图 11所示, 相关执行引擎分为3类, 包括基于有向无环图的大数据处理系统、基于关系代数的数据库执行引擎以及高性能计算系统.
|
图 11 执行引擎概览 |
4.1 大数据处理系统
最为广泛使用的执行引擎为大数据处理系统, 包括MapReduce (Hadoop)[70]、Dryad[71]、Spark[72]、Flink、H2O[73]. 这类系统面向通用数据分析负载, 能够灵活地支持复杂的矩阵计算操作. 此外, 这些系统均有开源社区支持, 软件栈生态成熟, 提供了丰富的第三方工具(例如数据迁移、集群监控)支持, 便于用户使用. 更重要的是, 大数据处理系统可轻松扩展至上千台机器, 并且对硬件要求宽松, 有成熟的容错能力, 适合面向大规模廉价集群或云平台的分布式矩阵计算系统. 此外, 不同的大数据处理系统也有其各自的优势特点. 以具有代表性的Spark与Flink为例, 前者是当下最流行的批处理系统, 而后者能够支持数据分析算法中常见的迭代语义, 并对迭代的执行过程进行了优化(如增量计算模式). 分布式矩阵计算系统需要在此之间进行取舍, 也有系统(如SystemDS)同时支持多种执行引擎, 由用户来进行决策.
4.2 数据库执行引擎现有的数据库执行引擎可分为两类: 第1类是通用数据库执行引擎, 包括PostgresQL[74]、MySQL[75]、Greenplum[76]. 这些执行引擎的最大优势在于它们所依附的数据库应用广泛, 往往是数据源, 因此直接在数据库上嵌入矩阵计算的相关实现可避免将数据从数据库迁移至执行引擎的步骤, 同时也可避免对数据库与执行引擎两套系统的维护成本. 然而, 这些执行引擎缺乏针对多维数据计算的优化, 为了解决这一问题, 该领域随后也出现了专门为科学计算设计的数据库执行引擎, 包括RIOT[77]与SciDB. 这些执行引擎围绕科学计算中一次写入、多次读取的特点进行设计, 针对多维矩阵构建专门的检索机制, 从而提高其执行效率. 但是由于需将线性代数转换为关系代数, 所以这些执行引擎所支持的操作类型仍然有限, 不适合处理复杂的算法逻辑.
4.3 高性能计算系统高性能计算系统是一类专门针对高硬件配置的超级计算机集群进行设计的执行引擎, 如ScaLAPACK[78]、PETSc[79]. 相较于前两种引擎, 这类引擎充分发挥网络通信设备高带宽的优势, 更注重对计算效率的优化, 从而在超级计算机集群上高效地执行分布式计算逻辑. 然而与此同时, 这类引擎依托高性能硬件将所有数据存放在内存中, 同时又缺乏针对网络通信超时等任务故障情况的处理措施, 因此容错能力不如前两种引擎, 仅适用于小规模的高可靠的集群. 此外, 不同的高性能计算系统适用于不同的应用场景, 例如ScaLAPACK适合处理稠密数据, 而PETSc则适合处理稀疏数据(如大规模网络的邻接矩阵).
综上, 目前的执行引擎种类、特点繁多, 对应地, 目前的分布式矩阵计算系统可根据所面向的用户、硬件和应用, 针对性地选择合适的执行引擎.
4.4 小结与分析表 3从软件栈生态、使用的硬件档次以及容错能力这3个方面分析了前述分布式矩阵计算系统的执行引擎, 展示了这些系统之间的共性和差异. 其中, RIOT为学术原型并未开源, 无法全面了解其执行引擎的具体情况, 故未在此列出.
| 表 3 对系统的执行引擎的总结 |
● 软件栈生态. 执行引擎的软件栈生态, 是影响用户开发成本的一项重要因素. 以SystemDS为例, 该系统以大数据系统Spark为执行引擎, 归功于开源社区的贡献, 其上下游的软件栈支持丰富, 包含从上层的数据分析工具到下层的文件系统和数据导入工具. SystemDS用户可通过这些工具方便地将SystemDS接入他们的工作流中. 类似地, MADlib以开源数据库PostgreSQL与Greenplum为执行引擎, 依托这两个数据库活跃的开源社区, MADlib同样拥有丰富的上下层软件工具, 便于数据库用户使用.相较之下, SciDB自研的执行引擎与pbdR所采用的ScaLAPACK的软件栈生态支持则略显不足, 用户需要自行开发上下层的对接工具, 加大了开发成本.
● 适用的硬件档次. 根据所面向的用户群体、应用场景的不同, 系统侧重的硬件环境也有所不同. 对应地, 系统应选择合适的执行引擎, 以充分利用各种档次的硬件的特点提升系统性能. 总体来说, 包含SystemDS、MADlib、SciDB在内的一类系统面向的是拥有大量廉价服务器或云平台资源的用户, 因此所选择的执行引擎拥有高扩展性, 且注重优化运行过程中的数据传输开销和内存占用等廉价硬件上常见的性能问题. 而包含pbdR在内的一类系统则面向的是拥有超级计算机集群资源的用户, 所以它们的执行引擎侧重于发挥高档硬件的优势, 例如利用内存空间大的优势采用纯内存计算, 以及优化缓存机制来提升对高档计算资源的利用率.
● 容错能力. 大数据分析应用往往需要长时间的运算处理, 在此期间更有可能发生故障. 而系统若要尽快地从故障中恢复以继续进行运算, 就需要具备一定的容错能力. 容错能力最高的一类系统包括SystemDS, 该系统依托Spark的容错机制, 能在分布式矩阵计算发生故障时, 针对当前的子任务进行重试, 避免了重新运行一遍完整的用户脚本. 而包含MADlib、SciDB在内的一类系统则依赖于执行引擎中的副本机制实现容错, 但是当所有副本均发生故障时, 这类系统需要重新运行脚本, 因此容错能力不如前者. 而最后, 包含pbdR在内的一类系统则缺乏成熟的容错机制, 更依赖于硬件本身的可靠性, 以避免故障的发生.
● 对稀疏矩阵操作的支持. 现有系统的执行引擎通常均支持稠密矩阵操作, 但是对稀疏矩阵操作的支持程度却不尽相同. 支持程度最高的一类系统包括SystemDS、MADlib, 所有矩阵操作均支持稀疏矩阵. 而SciDB仅对部分操作开放稀疏矩阵, 因此支持程度低于前者. pbdR等以ScaLAPACK为执行引擎的系统则只面向稠密矩阵计算, 即无论矩阵是否稀疏, 都将其视为稠密矩阵进行处理, 因此盲目地使用这类系统可能会碰到稀疏数据导致的内存占用过大或数据传输开销过大等性能问题.
5 数据存储如何在集群中组织、存储分布式矩阵, 对系统性能至关重要. 接下来, 本文将从矩阵单元分割、矩阵单元格式、矩阵分区方式这3个方面进行介绍.
5.1 矩阵单元分割作为组织数据的最小单位, 一个矩阵单元的大小从3个方面影响了系统的性能表现.
(1) 矩阵单元大小会直接影响内存占用: 单元设置得过大会导致内存溢出; 同时, 单元设置得过小也会导致系统需要维护大量结构数据(例如单元索引), 进而提高总内存占用.
(2) 单元大小决定了一个分布式矩阵会被分割为多少个单元: 单元设置得过小(即单元数过大), 会加剧分布式矩阵计算操作中的网络通信开销.
(3) 单元大小同时也决定了最大并行度: 单元设置得过大, 会导致单元数(即最大并行度)小于集群的并行度, 无法充分利用集群的计算资源.
基础的做法是, 系统预设一个固定的单元大小. 这类做法分为3种, 如图 12所示.

|
图 12 固定矩阵单元大小的基础分割方式 |
➢ 第1种做法是将一个分布式矩阵划分为多个固定的1000×1000的矩阵单元[9], 由于每个单元是方阵, 因此可以简化矩阵转置的操作.
➢ 第2种做法是将矩阵中一(或多)行(或列)作为一个单元, 适用于仅需按行或按列访问的矩阵[10].
➢ 第3种做法则更加极端, 是将每个元素作为一个单元. 这样做能够加快某些特定的操作(例如三对角化操作)[23], 但是在矩阵分解等常见算法中, 该做法的性能不如将矩阵按块分割的操作[17]. 此外, 该做法适合应用于极其稀疏的矩阵, 这样系统中仅需存储非零项的单元.
显然, 上述固定的分割方式得到的单元大小无法应对所有的数据规模和硬件环境, 因此往往不是最优的.为此, 目前已有不少工作针对运行环境和负载情况对自动单元大小进行调整.
➢ 一类工作以优化通信开销与内存占用为目标. 其中, SUMMA[80]针对网格或环形的集群架构, 分析分布式矩阵计算操作中的网络通信, 以得到性能最优的单元大小. 然而, 该技术在更通用的层次架构的集群上表现不佳[81]. 在层次架构下, CARMA[82]根据内存是否充足以及矩阵的不同形状(例如瘦高型), 分别制定了通信量最小的单元大小设置方法.
➢ 另一类工作则以权衡并行度与内存开销为目标. 为保障集群运算的最小并行度, DMac限制了单元的最小大小, 在此基础上最小化内存占用. 而MATFAST则将最小的单元大小设置为1 000, 在此基础上尽可能地提升并行度.
此外, 上述工作分割出的大部分矩阵单元的长宽是一样的. 然而, 在数据极度倾斜的稀疏矩阵上, 这种分割会导致有些矩阵单元内几乎没有非零项, 而有些单元则十分拥挤, 不利于批处理执行矩阵计算. 为此, 李亿渊等人[83]提出了针对稀疏矩阵的分割方法, 尽可能保证各个单元的大小、非零项个数接近.
5.2 矩阵单元格式为了最小化内存占用, 分布式矩阵计算系统需要为不同稀疏度的矩阵设置不同的矩阵单元格式, 其中, 稠密矩阵通过二维数组存放即可, 而稀疏矩阵的存储则更加复杂.
稀疏存储格式的基本思路是, 通过忽略单元中的零项以节省空间. 其中, 为分布式矩阵计算系统广泛采用的是稀疏行/列压缩格式(CSR/CSC). 以CSR为例, 该格式需要维护3个一维数组: 前两个数组按先行后列的顺序分别存放所有非零项数值与其对应的列号, 第3个数组则作为查询索引保留每行第1项在前两个数组中的位置(如图 13所示). 若一个单元是m×n的矩阵块, 那么随机访问CSR格式数据的复杂度是O(n), 其中, 通过索引数组找到所需行的复杂度为O(1), 从该行第1项遍历搜索对应列的复杂度为O(n). 然而, 该存储格式中要求非零项按顺序存储, 所以仅适用于后续无须添加元素的矩阵单元. 进一步地, SystemDS基于CSR格式提出了MCSR格式[9], 旨在支持增量地往矩阵单元中添加元素. 相较于原本的CSR格式, MCSR格式无须按顺序存储非零项, 但是其代价是更高的内存占用以及内存带宽要求. 此外, CSR格式中的索引数组长度固定为m, 当矩阵极其稀疏时, 仍会浪费内存空间. 在这种情况下, 坐标压缩格式(COO)用一个三维数组维护所有非零项的行号与列号, 能够最大程度地节省内存, 并且支持增量地添加元素. 其缺陷也同样明显, COO格式下随机访问、按行访问或按列访问的复杂度均为O(mn), 对内存带宽的要求最高.

|
图 13 CSR示例 |
此外, 矩阵单元格式也可针对某些特殊的矩阵结构进行特定的优化. 具体来说, SLATE专门为梯形/三角矩阵和对称/厄米特矩阵设计了特定的存储格式. 具体来说, 在梯形/三角矩阵中, 虽然整体是稀疏矩阵, 但是矩阵的非零部分是稠密的, 因此仅非零部分按照稠密格式存储. 而在对称/厄米特矩阵中, 系统仅需存储一半的数据, 另一半可推算得到.
5.3 矩阵分区方式由于分布式矩阵计算中经常会出现连接、聚合矩阵元素的操作, 因此, 如何设置矩阵的单元分区方式至关重要. 一种合适的分区方式可以显著降低分布式矩阵计算的网络通信开销, 进而提升性能. 基础的分区方式包括:
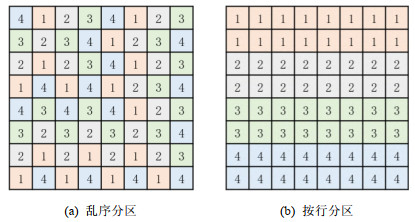
(1) 乱序分区, 例如通过哈希函数分配单元所处分区[9], 或按“之”字形分区[84], 如图 14(a)所示. 该方式可以将数据平均地分散在各个分区, 保障负载平衡, 但同时, 该方式导致分区内的单元几乎都是不连续的, 影响执行效率.
|
图 14 分区数为4的基础分区方式示例 |
(2) 按行/列分区, 将行/列索引相同的单元分配到同一个分区上[30], 如图 14(b)所示. 该方式利于提升部分分布式矩阵计算操作, 例如在矩阵乘法中需要聚合相同行/列的单元, 按行/列分区则可以避免聚合操作带来的网络通信开销. 然而, 大规模矩阵往往是稀疏且非零项分布不均匀的, 这种分区方式可能会导致负载不均衡的情况出现.
不同的分区方式适用于不同的算子操作, 例如, 按行分区适合统计行平均值的算子. 为了让系统能够自动选取最优的分区方式, DMac、MATFAST与BlockJoin[85]根据执行计划中各个算子的依赖关系, 制定矩阵的分区方式. 具体来说, 它们首先分析适合各个算子的输入分区方式, 其次, 利用算子中间的shuffle操作尽可能调整上游算子输出的分区方式, 即利于下游算子的输入分区. DistME[86]则针对矩阵乘法操作设计了更为灵活的策略, 该工作采用一种网格分区方式, 该方式将矩阵分区为多个矩形网格. DistME根据矩阵乘法的需要自动调整网格的长宽, 从而降低网络通信. 值得注意的是, 其中, 按行/列分区可视为网格分区的一种特殊情况, 即一个网格就是一行/列.
5.4 小结与分析表 4从执行效率和存储空间占用两个方面分析了前述分布式矩阵计算系统的数据存储, 展示了这些系统之间的共性和差异.
| 表 4 对系统的数据存储的总结 |
● 对执行效率的提升. 上述系统按对执行效率的提升可分为3个档次: 提升最高的一类系统包括DMac、MATFAST、BlockJoin、DistME, 它们通过优化数据分区的方式, 显著提升了算子执行时的中间数据传输开销; 相较之下, SUMMA仅针对特定的集群架构优化数据存储方式, 有局限性, CARMA仅优化了矩阵的单元大小, 而SystemDS则仅采用了基础的数据存储方式来提升部分执行效率, 因此它们的提升档次居中; SLATE则并没有专门针对执行效率问题优化数据存储方式.
● 对存储空间占用的优化. 类似地, 上述系统按对存储空间占用的优化可分为3个档次: 优化最好的一类系统包括CARMA、DMac、SLATE, 它们自适应地调整矩阵单元以最小化对存储空间的占用; SystemDS则采取了相对基础、保守的方式设置数据存储方式, 故优化效果略逊于前者; SUMMA、BlockJoin、DistME则没有专门针对存储空间占用问题优化数据存储方式.
6 总体分析与未来展望 6.1 总体分析从整体来看, 分布式矩阵计算系统的相关工作致力于改进系统的两个方面, 也是用户最关心的, 即编程接口用起来是否方便和系统性能是否满足需求. 因此, 本节将从这两方面总结分析目前功能成熟且广泛使用的一批开源系统, 包括pbdR、MLlib、SystemDS、MADlib、SciDB. 此外, 如表 5所示, 本节也将进一步探讨这些系统各自的适用场景.
| 表 5 对开源系统的总体分析 |
● 首先, 从编程角度来看, SystemDS是最易使用的, 用户完全不用考虑分布式计算逻辑; pbdR也相对易用, 仅需要用户自行区别分布式矩阵和单机矩阵; 而剩余的系统就暴露了更多繁杂的分布式计算逻辑.
● 其次, 从性能角度来看, 根据现有的系统评测[87]以及本文作者的相关工作中的实验结果[18, 51].
➢ SystemDS凭借其优化技术, 能够在几乎所有负载下取得最优或近优的性能.
➢ pbdR与SciDB能够在稠密矩阵计算负载中取得与SystemDS相近的性能, 但缺少对稀疏矩阵计算的支持.
➢ MADlib与MLlib的性能则相对不足, 其中, MADlib由于执行引擎的缘故, 需要通过读写磁盘的方式传递中间结果, 导致不必要的中间结果物化和磁盘读写开销; 而MLlib由于其复杂的调优选项(例如, 需要对每个矩阵调整其单元格式、分区方式或数量、缓存机制), 难以取得最优的性能.
因此, 总体上, SystemDS是目前较为易用且性能优异的分布式矩阵计算系统, 但其余系统也有其各自适用的场景: 归功于pbdR轻量级的部署与简便的编程接口, 用户可以通过pbdR快速扩展、运行/测试原本的单机算法; MLlib适用于原本就基于Spark生态构建的工作流; MADlib允许用户直接在数据库中用矩阵计算逻辑处理数据; 而SciDB则适合处理科学计算应用中的大规模多维张量.
6.2 未来展望分布式矩阵计算系统具有广泛的应用前景, 本节简要讨分布式矩阵计算系统未来可能的发展方向.
● 迎接深度学习应用对于矩阵计算的新型需求. 现有的分布式矩阵计算系统重视矩阵乘法等简单批量操作的优化, 然而, 时下最流行的深度学习应用中还涉及卷积计算等更复杂的操作, 矩阵计算系统目前还缺乏对这些操作的成熟支持[87]. 此外, 深度学习应用对数据集的访问通常以重复采样的形式进行, 而矩阵计算系统则擅长对整个数据集进行批量处理[88]. 因此, 如何应对深度学习应用的新型需求, 是未来值得关注的发展方向.
● 挖掘与底层执行引擎深度融合的潜在动能. 现有的分布式矩阵计算系统主要侧重于如何发挥底层执行引擎的作用, 与执行引擎的耦合度相对较低. 本文中提到的诸多系统(如SystemDS、HyMAC、DMac、MATFAST)均依赖于底层Spark的接口来实现自身的优化技术. 然而, Spark作为一个独立的面向通用计算的平台, 无法感知矩阵计算应用的特点, 自然也无法针对性地优化底层的执行过程. 一个典型的例子是, 上层矩阵计算系统无法直接管理Spark中数据和算子的物理位置, 仅能通过接口管理其逻辑位置. 因此, 分布式矩阵计算系统仍然存在潜在的性能提升空间, 可通过深度融合矩阵计算应用与底层执行引擎进一步挖掘.
● 发挥硬件加速器为矩阵计算带来的强大算力. 目前, 新型硬件加速器层出不穷, 相较于CPU, 这些加速器提供了更高的计算并行度, 且更善于处理无分枝的运算逻辑, 十分贴合矩阵计算的应用场景. 尽管已有不少工作提出了基于新硬件加速器的优化技术[86, 89], 但是这些工作大多聚焦某个算子或算法.如何基于新硬件加速器构建完整的系统, 仍然值得研究.
7 结束语本文首先回顾了矩阵计算系统的发展历程, 突出了新兴的分布式矩阵计算系统在大数据治理中的关键作用; 然后, 本文参考了数据管理领域的研究思路, 从数据管理视角分析了分布式矩阵计算系统面临的挑战以及相关技术分类; 随后, 详细介绍、总结了各个分类下的现有技术如何解决前述挑战; 最后, 本文总体分析了典型的分布式矩阵计算系统, 并展望了未来的研究方向.
| [1] |
Sylvester J. On a new class of theorems. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1850, 37: 363-370.
[doi:10.1080/14786445008646629] |
| [2] |
Cayley A. A memoir on the theory of matrices. Philosophical Trans. of the Royal Society of London, 1858, 31(148): 17-37.
|
| [3] |
Gu R, Qiu HJ, Yang WJ, Hu W, Yuan CF, Huang YH. Goldfish: A large scale semantic data store and query system based on Boolean matrix factorization. Chinese Journal of Computers, 2017, 40(10): 2212-2230(in Chinese with English abstract).
[doi:10.11897/SP.J.1016.2017.02212] |
| [4] |
Shen XW, Ye XC, Wang D, Zhang H, Wang F, Tan X, Zhang ZM, Fan DR, Tang ZM, Sun NH. Optimizing dataflow architecture for scientific applications. Chinese Journal of Computers, 2017, 40(9): 2181-2196(in Chinese with English abstract).
https://www.cnki.com.cn/Article/CJFDTOTAL-JSJX201709014.htm |
| [5] |
Big data analytics market. https://www.fortunebusinessinsights.com/big-data-analytics-market-106179
|
| [6] |
Abadi M, Barham P, Chen J, Chen Z, Davis A, Dean J, Devin M, Ghemawat S, Irving G, Isard M, Kudlur M. TensorFlow: A system for large-scale machine learning. In: Proc. of the 12th USENIX Symp. on Operating Systems Design and Implementation. Savannah: USENIX, 2016. 265-283.
|
| [7] |
PyTorch. https://github.com/pytorch/pytorch
|
| [8] |
Hellerstein J, Re C, Schoppmann F, Wang DZ, Fratkin E, Gorajek A, Ng KS, Welton C, Feng X, Li K, Kumar A. The MADlib analytics library or MAD skills, the SQL. Proc. of the VLDB Endowment, 2012, 5(12): 1700-1711.
[doi:10.14778/2367502.2367510] |
| [9] |
Boehm M, Dusenberry MW, Eriksson D, Evfimievski AV, Manshadi FM, Pansare N, Reinwald B, Reiss FR, Sen P, Surve AC, Tatikonda S. SystemML: Declarative machine learning on spark. Proc. of the VLDB Endowment, 2016, 9(13): 1425-1436.
[doi:10.14778/3007263.3007279] |
| [10] |
Bosagh Zadeh R, Meng X, Ulanov A, Yavuz B, Pu L, Venkataraman S, Sparks ER, Staple A, Zaharia M. Matrix computations and optimization in apache spark. In: Proc. of the 22nd ACM SIGKDD Int'l Conf. on Knowledge Discovery and Data Mining. San Francisco: ACM, 2016. 31-38.
|
| [11] |
Schelter S, Palumbo A, Quinn S, Marthi S, Musselman A. Samsara: Declarative machine learning on distributed dataflow systems. In: Proc. of the 30th Conf. on Neural Information Processing Systems. Barcelona: Curran Associates Inc., 2016.
|
| [12] |
Chen L, Kumar A, Naughton J, Patel JM. Towards linear algebra over normalized data. Proc. of the VLDB Endowment, 2016, 10(11): 1214-1225.
|
| [13] |
Gan J, Liu T, Li L, Zhang J. Non-negative matrix factorization: A survey. The Computer Journal, 2021, 64(7): 1080-1092.
[doi:10.1093/comjnl/bxab103] |
| [14] |
Gou P, Wang K, Luo AL, Xue MZ. Computational intelligence for big data analysis: Current status and future prospect. Ruan Jian Xue Bao/Journal of Software, 2015, 26(11): 3010-3025(in Chinese with English abstract).
http://www.jos.org.cn/1000-9825/4900.htm [doi:10.13328/j.cnki.jos.004900] |
| [15] |
Qian Z, Chen, X, Kang N, Chen M, Yu Y, Moscibroda T, Zhang Z. MadLINQ: Large-scale distributed matrix computation for the cloud. In: Proc. of the 7th ACM European Conf. on Computer Systems. Bern: ACM, 2012. 197-210.
|
| [16] |
Venkataraman S, Bodzsar E, Roy I, AuYoung A, Schreiber RS. Presto: Distributed machine learning and graph processing with sparse matrices. In: Proc. of the 8th ACM European Conf. on Computer Systems. Prague: ACM, 2013. 197-210.
|
| [17] |
Bosilca G, Bouteiller A, Danalis A, Faverge M, Haidar A, Herault T, Kurzak J, Langou J, Lemarinier P, Ltaief H, Luszczek P, YarKhan A, Dongarra J. Flexible development of dense linear algebra algorithms on massively parallel architectures with DPLASMA. In: Proc. of the IEEE Int'l Symp. on Parallel and Distributed Processing Workshops and Phd Forum. Anchorage: IEEE, 2011. 1432-1441.
|
| [18] |
Chen Z, Xu C, Soto J, Markl V, Qian W, Zhou A. Hybrid evaluation for distributed iterative matrix computation. In: Proc. of the ACM Int'l Conf. on Management of Data. Xi'an: ACM, 2021. 300-312.
|
| [19] |
Das S, Sismanis Y, Beyer KS, Gemulla R, Haas PJ, McPherson J. Ricardo: Integrating R and hadoop. In: Proc. of the ACM Int'l Conf. on Management of Data. Indianapolis: ACM, 2010. 987-998.
|
| [20] |
Venkataraman S, Yang Z, Liu D, Liang E, Falaki H, Meng X, Xin R, Ghdsi A, Franklin M, Stoica I, Zaharia M. SparkR: Scaling R programs with spark. In: Proc. of the ACM Int'l Conf. on Management of Data. San Francisco: ACM, 2016. 1099-1104.
|
| [21] | |
| [22] |
Programming with big data in R. https://pbdr.org/
|
| [23] |
Poulson J, Marker B, Van de Geijn RA, Hammond JR, Romero NA. Elemental: A new framework for distributed memory dense matrix computations. ACM Trans. on Mathematical Software, 2013, 39(2): 1-24.
|
| [24] |
Boehm M, Burdick DR, Evfimievski AV, Reinwald B, Reiss F, Sen P, Tatikonda S, Tian Y. SystemML's optimizer: Plan generation for large-scale machine learning programs. IEEE Data Engineering Bulletin, 2014, 37(3): 52-62.
|
| [25] |
Boehm M, Antonov I, Baunsgaard S, Dokter M, Ginthor R, Innerebner K, Lindstaedt SN, Phani A, Rath B, Reinwald B, Siddiqui S, Wrede SB. SystemDS: A declarative machine learning system for the end-to-end data science lifecycle. In: Proc. of the 10th Biennial Conf. on Innovative Data Systems Research. 2020.
|
| [26] |
Wang J, Wu J, Li M, Gu J, Das A, Zaniolo C. Formal semantics and high performance in declarative machine learning using datalog. The VLDB Journal, 2021, 30: 859-881.
[doi:10.1007/s00778-021-00665-6] |
| [27] |
DistArrays. http://docs.enthought.com/distarray/
|
| [28] |
Huang CC, Chen Q, Wang Z, Power R, Ortiz J, Li J, Xiao Z. Spartan: A distributed array framework with smart tiling. In: Proc. of the USENIX Annual Technical Conf. Santa Clara: USENIX, 2015. 1-15.
|
| [29] |
Sparks ER, Talwalkar A, Smith V, Kottalam J, Pan X, Gonzalez JE, Franklin MJ, Jordan MI, Kraska T. MLI: An API for distributed machine learning. In: Proc. of the IEEE 13th Int'l Conf. on Data Mining. Dallas: IEEE, 2013. 1187-1192.
|
| [30] |
Yu L, Shao Y, Cui B. Exploiting matrix dependency for efficient distributed matrix computation. In: Proc. of the ACM Int'l Conf. on Management of Data. Melbourne: ACM, 2015. 93-105.
|
| [31] |
Gates M, Kurzak J, Charara A, YarKhan A, Dongarra J. SLATE: Design of a modern distributed and accelerated linear algebra library. In: Proc. of the Int'l Conf. for High Performance Computing, Networking, Storage and Analysis. Denver: ACM, 2019. 26: 1-26: 18.
|
| [32] |
Agullo E, Aumage O, Faverge M, Furmento N, Pruvost F, Sergent M, Thibault SP. Achieving high performance on supercomputers with a sequential task-based programming model. IEEE Trans. on Parallel and Distributed Systems, 2017.
|
| [33] |
Armbrust M, Xin RS, Lian C, Huai Y, Liu D, Bradley JK, Meng X, Kaftan T, Franklin MJ, Ghodsi A, Zaharia M. Spark SQL: Relational data processing in spark. In: Proc. of the ACM Int'l Conf. on Management of Data. Melbourne: ACM, 2015. 1383-1394.
|
| [34] | |
| [35] |
Brown PG. Overview of SciDB: Large scale array storage, processing and analysis. In: Proc. of the ACM Int'l Conf. on Management of Data. Indianapolis: ACM, 2010. 963-968.
|
| [36] |
Alotaibi R, Cautis B, Deutsch A, Manolescu I. HADAD: A lightweight approach for optimizing hybrid complex analytics queries. In: Proc. of the ACM Int'l Conf. on Management of Data. Xi'an: ACM, 2021. 23-35.
|
| [37] |
Low Y, Gonzalez J, Kyrola A, Bickson D, Guestrin C, Hellerstein JM. Distributed GraphLab: A framework for machine learning in the cloud. Proc. of the VLDB Endowment, 2012, 5(8): 716-727.
[doi:10.14778/2212351.2212354] |
| [38] |
Malewicz G, Austern MH, Bik AJ, Dehnert JC, Horn I, Leiser N, Czajkowski G. Pregel: A system for large-scale graph processing. In: Proc. of the ACM Int'l Conf. on Management of Data. Indianapolis: ACM, 2010. 135-146.
|
| [39] |
Carbone P, Katsifodimos A, Ewen S, Markl V, Haridi S, Tzoumas K. Apache Flink: Stream and batch processing in a single engine. Bulletin of the IEEE Computer Society Technical Committee on Data Engineering, 2015, 36(4): 28-38.
|
| [40] |
Ewen S, Tzoumas K, Kaufmann M, Markl V. Spinning fast iterative data flows. Proc. of the VLDB Endowment, 2012, 5(12): 1268-1279.
|
| [41] |
Mihaylov SR, Ives ZG, Guha S. REX: Recursive, delta-based data-centric computation. Proc. of the VLDB Endowment, 2012, 5(11): 1280-1291.
[doi:10.14778/2350229.2350246] |
| [42] |
McSherry F, Murray DG, Isaacs R, Isard M. Differential dataflow. In: Proc. of the 6th Biennial Conf. on Innovative Data Systems Research. 2013.
|
| [43] |
Murray DG, McSherry F, Isaacs R, Isard M, Barham P, Abadi M. Naiad: A timely dataflow system. In: Proc. of the 24th ACM Symp. on Operating Systems Principles. Farmington: ACM, 2013. 439-455.
|
| [44] |
Nikolic M, Elseidy M, Koch C. LINVIEW: Incremental view maintenance for complex analytical queries. In: Proc. of the ACM Int'l Conf. on Management of Data. Snowbird: ACM, 2014. 253-264.
|
| [45] |
Nikolic M, Olteanu D. Incremental view maintenance with triple lock factorization benefits. In: Proc. of the ACM Int'l Conf. on Management of Data. Houston: ACM, 2018. 365-380.
|
| [46] |
Kunft A, Katsifodimos A, Schelter S, Breß S, Rabl T, Markl V. An intermediate representation for optimizing machine learning pipelines. Proc. of the VLDB Endowment, 2019, 12(11): 1553-1567.
[doi:10.14778/3342263.3342633] |
| [47] |
Yu Y, Tang M, Aref WG, Malluhi QM, Abbas MM, Ouzzani M. In-memory distributed matrix computation processing and optimization. In: Proc. of the IEEE 33rd Int'l Conf. on Data Engineering. San Diego: IEEE, 2017. 1047-1058.
|
| [48] |
Wang YR, Hutchison S, Suciu D, Howe B, Leang J. SPORES: Sum-product optimization via relational equality saturation for large scale linear algebra. Proc. of the VLDB Endowment, 2020, 13(11): 1919-1932.
|
| [49] |
Green TJ, Karvounarakis G, Tannen V. Provenance semirings. In: Proc. of the 26th ACM-SIGACT-SIGART Symp. on Principles of Database Systems. Santa Barbara: ACM, 2007. 31-40.
|
| [50] |
Tate R, Stepp M, Tatlock Z, Lerner S. Equality saturation: A new approach to optimization. In: Proc. of the 36th Annual ACM SIGPLAN-SIGACT Symp. on Principles of Programming Languages. Savannah: ACM, 2009. 264-276.
|
| [51] |
Chen Z, Xu C, Qian W, Zhou A. Redundancy elimination in distributed matrix computation. In: Proc. of the ACM Int'l Conf. on Management of Data. Philadelphia: ACM, 2022. 573-586.
|
| [52] |
Karsavuran MO, Akbudak K, Aykanat C. Locality-aware parallel sparse matrix-vector and matrix-transpose-vector multiplication on many-core processors. IEEE Trans. on Parallel and Distributed Systems, 2015, 27(6): 1713-1726.
|
| [53] |
Han D, Lee J, Kim M. FuseME: Distributed matrix computation engine based on cuboid-based fused operator and plan generation. In: Proc. of the ACM Int'l Conf. on Management of Data. Philadelphia: ACM, 2022. 1891-1904.
|
| [54] |
Huang B, Babu S, Yang J. Cumulon: Optimizing statistical data analysis in the cloud. In: Proc. of the ACM Int'l Conf. on Management of Data. New York: ACM, 2013. 1-12.
|
| [55] |
Belter G, Jessup ER, Karlin I, Siek JG. Automating the generation of composed linear algebra kernels. In: Proc. of the Conf. on High Performance Computing Networking, Storage and Analysis. Portland: Association for Computing Machinery, 2009. 1-12.
|
| [56] |
Sujeeth AK, Lee HJ, Brown KJ, Rompf T, Chafi H, Wu M, Atreya AR, Odersky M, Olukotun K. OptiML: An implicitly parallel domain-specific language for machine learning. In: Proc. of the 28th Int'l Conf. on Machine Learning. Washington: Omnipress, 2011. 609-616.
|
| [57] |
Zhang M, Wu Y, Chen K, Ma T, Zheng W. Measuring and optimizing distributed array programs. Proc. of the VLDB Endowment, 2016, 9(12): 912-923.
[doi:10.14778/2994509.2994511] |
| [58] |
Crotty A, Galakatos A, Dursun K, Kraska T, Binnig C, Cetintemel U, Zdonik S. An architecture for compiling UDF-centric workflows. Proc. of the VLDB Endowment, 2015, 8(12): 1466-1477.
|
| [59] |
Palkar S, Thomas JJ, Shanbhag A, Narayanan D, Pirk H, Schwarzkopf M, Amarasinghe S, Zaharia M. Weld: A common runtime for high performance data analytics. In: Proc. of the 8th Biennial Conf. on Innovative Data Systems Research. 2017.
|
| [60] |
Vasilache N, Zinenko O, Theodoridis T, Goyal P, DeVito Z, Moses WS, Verdoolaege S, Adams A, Cohen A. Tensor comprehensions: Framework-agnostic high-performance machine learning abstractions. arXiv: 1802.04730, 2018.
|
| [61] |
Elgamal T, Luo S, Boehm M, Evfimievski AV, Tatikonda S, Reinwald B, Sen P. SPOOF: Sum-product optimization and operator fusion for large-scale machine learning. In: Proc. of the 8th Biennial Conf. on Innovative Data Systems Research. 2017.
|
| [62] |
Boehm M, Reinwald B, Hutchison D, Hutchison D, Sen P, Evfimievski AV, Pansare N. On optimizing operator fusion plans for large-scale machine learning in SystemML. Proc. of the VLDB Endowment, 2018, 11(12): 1755-1768.
|
| [63] |
Matlab mmtimes function. https://ww2.mathworks.cn/matlabcentral/fileexchange/27950-mmtimes-matrix-chain-product
|
| [64] |
Sommer J, Boehm M, Evfimievski AV, Reinwald B, Haas PJ. MNC: Structure-exploiting sparsity estimation for matrix expressions. In: Proc. of the Int'l Conf. on Management of Data. Amsterdam: ACM, 2019. 1607-1623.
|
| [65] |
Ghoting A, Krishnamurthy R, Pednault EPD, Reinwald B, Sindhwani V, Tatikonda S, Tian Y, Vaithyanathan S. SystemML: Declarative machine learning on MapReduce. In: Proc. of the 27th IEEE Int'l Conf. on Data Engineering. Hannover: IEEE, 2011. 231-242.
|
| [66] |
Liao X, Li SG, Lu YT, Yang CQ. New 2.5D parallel matrix multiplication algorithm based on BLACS. Chinese Journal of Computers, 2020, 44(5): 1037-1050(in Chinese with English abstract).
https://www.cnki.com.cn/Article/CJFDTOTAL-JSJX202105013.htm |
| [67] |
Feng J, Ni M, Zhao JB. Algorithm of distributed matrix multiplication based on hadoop. Computer Systems Applications, 2013, 22(12): 149-154(in Chinese with English abstract).
https://www.cnki.com.cn/Article/CJFDTOTAL-XTYY201312029.htm |
| [68] |
Gu R, Tang Y, Tian C, Zhou H, Li G, Zheng X, Huang Y. Improving execution concurrency of large-scale matrix multiplication on distributed data-parallel platforms. IEEE Trans. on Parallel and Distributed Systems, 2017, 28(9): 2539-2552.
|
| [69] |
Kwasniewski G, Kabic M, Ben-Nun T, Ziogas AN, Saether JE, Gaillard A, Schneider T, Besta M, Kozhevnikov A, VandeVondele J, Hoefler T. On the parallel I/O optimality of linear algebra kernels: Near-optimal matrix factorizations. In: Proc. of the Int'l Conf. for High Performance Computing, Networking, Storage and Analysis. St. Louis: ACM, 2021. 70: 1-70: 15.
|
| [70] |
Dean J, Ghemawat S. MapReduce: Simplified data processing on large clusters. Communications of the ACM, 2008, 51(1): 107-113.
|
| [71] |
Isard M, Budiu M, Yu Y, Birrell A, Fetterly D. Dryad: Distributed data-parallel programs from sequential building blocks. In: Proc. of the 2nd ACM SIGOPS/EuroSys European Conf. on Computer Systems. Lisbon: ACM, 2007. 59-72.
|
| [72] |
Zaharia M, Chowdhury M, Das T, Dave A, Ma J, McCualy M, Franklin MJ, Shenker S, Stoica I. Resilient distributed datasets: A fault-tolerant abstraction for in-memory cluster computing. In: Proc. of the 9th USENIX Symp. on Networked Systems Design and Implementation. San Jose: USENIX, 2012. 15-28.
|
| [73] |
H2O. https://h2o.ai/
|
| [74] |
PostgreSQL. https://www.postgresql.org/
|
| [75] |
MySQL. https://www.mysql.com/
|
| [76] |
GreenPlum. https://tanzu.vmware.com/greenplum
|
| [77] |
Zhang Y, Herodotou H, Yang J. RIOT: I/O-efficient numerical computing without SQL. In: Proc. of the 4th Biennial Conf. on Innovative Data Systems Research. 2009.
|
| [78] |
ScaLAPACK. http://www.netlib.org/scalapack/
|
| [79] |
PETSc. https://petsc.org/release/
|
| [80] |
Van De Geijn RA, Watts J. SUMMA: Scalable universal matrix multiplication algorithm. Concurrency: Practice and Experience, 1997, 9(4): 255-274.
|
| [81] |
Ballard G, Demmel J, Holtz O, Lipshitz B, Schwartz O. Communication-optimal parallel algorithm for Strassen's matrix multiplication. In: Proc. of the 24th Annual ACM Symp. on Parallelism in Algorithms and Architectures. Pittsburgh: ACM, 2012. 193-204.
|
| [82] |
Demmel J, Eliahu D, Fox A, Kamil S, Lipshitz B, Schwartz O, Spillinger O. Communication-optimal parallel recursive rectangular matrix multiplication. In: Proc. of the IEEE 27th Int'l Symp. on Parallel and Distributed Processing. Cambridge: IEEE, 2013. 261-272.
|
| [83] |
Li YY, Xue W, Chen DX, Wang XL, Xu P, Zhang WS, Yang GW. Performance optimization for sparse matrix-vector multiplication on sunway architecture. Chinese Journal of Computers, 2020, 43(6): 1010-1024(in Chinese with English abstract).
https://www.cnki.com.cn/Article/CJFDTOTAL-JSJX202006003.htm |
| [84] |
Long GP, Fan DR. Parallelization of LU decomposition on the Godson-Tv1 many-core architecture. Chinese Journal of Computers, 2009, 32(11): 2157-2167(in Chinese with English abstract).
https://www.cnki.com.cn/Article/CJFDTOTAL-JSJX200911007.htm |
| [85] |
Kunft A, Katsifodimos A, Schelter S, Rabl T, Markl V. Blockjoin: Efficient matrix partitioning through joins. Proc. of the VLDB Endowment, 2017, 10(13): 2061-2072.
|
| [86] |
Han D, Nam Y, Lee J, Park K, Kim H, Kim M. DistME: A fast and elastic distributed matrix computation engine using GPUs. In: Proc. of the Int'l Conf. on Management of Data. Amsterdam: ACM, 2019. 759-774.
|
| [87] |
Thomas A, Kumar A. A comparative evaluation of systems for scalable linear algebra-based analytics. Proc. of the VLDB Endowment, 2018, 11(13): 2168-2182.
|
| [88] |
Han B, Chen Z, Xu C, Zhou A. Efficient matrix computation for SGD-based algorithms on apache spark. In: Proc. of the 27th Database Systems for Advanced Applications. Springer, 2022. 309-324.
|
| [89] |
Parger M, Winter M, Mlakar D, Steinberger M. SpECK: Accelerating GPU sparse matrix-matrix multiplication through lightweight analysis. In: Proc. of the 25th ACM SIGPLAN Symp. on Principles and Practice of Parallel Programming. San Diego: ACM, 2020. 362-375.
|
| [3] |
顾荣, 仇红剑, 杨文家, 胡伟, 袁春风, 黄宜华. Goldfish: 基于矩阵分解的大规模RDF数据存储与查询系统. 计算机学报, 2017, 40(10): 2212-2230.
[doi:10.11897/SP.J.1016.2017.02212] |
| [4] |
申小伟, 叶笑春, 王达, 张浩, 王飞, 谭旭, 张志敏, 范东睿, 唐志敏, 孙凝晖. 一种面向科学计算的数据流优化方法. 计算机学报, 2017, 40(9): 2181-2196.
https://www.cnki.com.cn/Article/CJFDTOTAL-JSJX201709014.htm |
| [14] |
郭平, 王可, 罗阿理, 薛明志. 大数据分析中的计算智能研究现状与展望. 软件学报, 2015, 26(11): 3010-3025.
http://www.jos.org.cn/1000-9825/4900.htm [doi:10.13328/j.cnki.jos.004900] |
| [66] |
廖霞, 李胜国, 卢宇彤, 杨灿群. 基于BLACS的2.5D并行矩阵乘法. 计算机学报, 2020, 44(5): 1037-1050.
https://www.cnki.com.cn/Article/CJFDTOTAL-JSJX202105013.htm |
| [67] |
冯健, 倪明, 赵建波. 一种基于分布式平台Hadoop的矩阵相乘算法. 计算机系统应用, 2013, 22(12): 149-154.
https://www.cnki.com.cn/Article/CJFDTOTAL-XTYY201312029.htm |
| [83] |
李亿渊, 薛巍, 陈德训, 王欣亮, 许平, 张武生, 杨广文. 稀疏矩阵向量乘法在申威众核架构上的性能优化. 计算机学报, 2020, 43(6): 1010-1024.
https://www.cnki.com.cn/Article/CJFDTOTAL-JSJX202006003.htm |
| [84] |
龙国平, 范东睿. LU分解在Godson-Tv1众核体系结构上的并行化研究. 计算机学报, 2009, 32(11): 2157-2167.
https://www.cnki.com.cn/Article/CJFDTOTAL-JSJX200911007.htm |
 2023, Vol. 34
2023, Vol. 34


