融媒体旨在整合存在共同点又存在互补性的媒体, 需要充分各种媒介载体, 实现“资源通融、内容兼融、宣传互融、利益共融”的新型媒体. 在这种需求之下, 针对各种媒体数据的智能处理是必然要面临的挑战. 近年来, 移动互联网的蓬勃发展带来了多媒体数据爆发式的增长. 这些数据不仅来源广泛, 而且内容和媒体形式也复杂多变. 在这种环境下, 如何更加精准地进行内容分析、建立不同媒体数据间的联系并服务于数据检索与分析等应用场景, 是实现融媒体的重要一环. 当今时代, 随着触摸屏设备的流行, 电子数据化的手绘草图变得越来越容易获取. 由于草图几乎可以由任何人费很小的代价画出, 且不涉及隐私和版权的问题, 对于融媒体实现具有很高的利用价值.

草图检索是利用草图的一个重要方向. 尽管草图表现出高度的抽象性, 它仍然包含足够的结构和外形信息来描述对象, 催生出使用草图从庞大的图像集中检索出所需内容的需求. 因此, 基于草图的图像检索(sketch-based image retrieval, SBIR)任务得到了越来越多的关注和研究. 现有的SBIR方法在可见类(即训练时所用数据的类别集合)数据上的检索效果表现良好, 但却难以应用到实际的应用场景. 第1原因在于“类别”这个概念广泛存在于现实场景中, 不可能收集到所有类别的数据. 第2原因在于这些方法在设计时只考虑训练数据的特点, 却未考虑方法的泛化性. 因此, 它们在零样本草图检索(zero-shot sketch-based image retrieval, ZS-SBIR)^[1]任务中被证实性能表现不佳.

对于ZS-SBIR任务, 模型训练于可见类数据, 但却测试于未见类数据. 这样的行为差异要求我们在模型设计和训练时, 既要考虑草图和图像数据形态上的模态差异, 也要考虑可见类和未见类的语义不一致性问题^[2]. 最近, 一些工作大部分只专注于解决模态差异^[3]问题, 对语义不一致性问题不够重视. 它们中的大部分工作^[4–8]都采取深度生成模型作为主要框架, 学习从模态的原始表征到公共嵌入空间^[9]的投影, 但忽略了之前由预训练模型获得的知识. 虽然Liu等人^[10]率先尝试利用知识蒸馏过程来保留丰富的视觉特征, 但他们的方法依旧是基于单模态知识蒸馏的想法. 由于目前没有大规模预训练的草图识别模型, 单模态知识蒸馏方法只能针对图像模态, 忽略了对草图的泛化性的重要性.

此外, 这些ZS-SBIR方法(除了Kiran等人的工作^[5])期望通过简单地利用语义嵌入, 以消除可见类和未见类的语义不一致性问题. 它们或者是从词向量模型中提取类名的词向量^{[1, 6, 8]}, 或者通过分层模型衡量类名的词相似性^[10], 或者以上二者的结合^[4]. 然而, 这有两方面的问题. 一方面是, 语义嵌入编码的信息大部分是文本信息, 但ZS-SBIR是视觉任务, 它的引导作用不是最优的. 另一方面在于, 从类名提取语义嵌入需要预先定义准确的类名, 并且需要额外的语言模型和时间消耗, 导致训练资源获取方面的负担. 然而, 在一些实际的应用场景中, 数据只能被数字标记(例如, 出于隐私原因), 或者类名是稀有词或复合词, 因而无法从语言模型中提取语义嵌入.

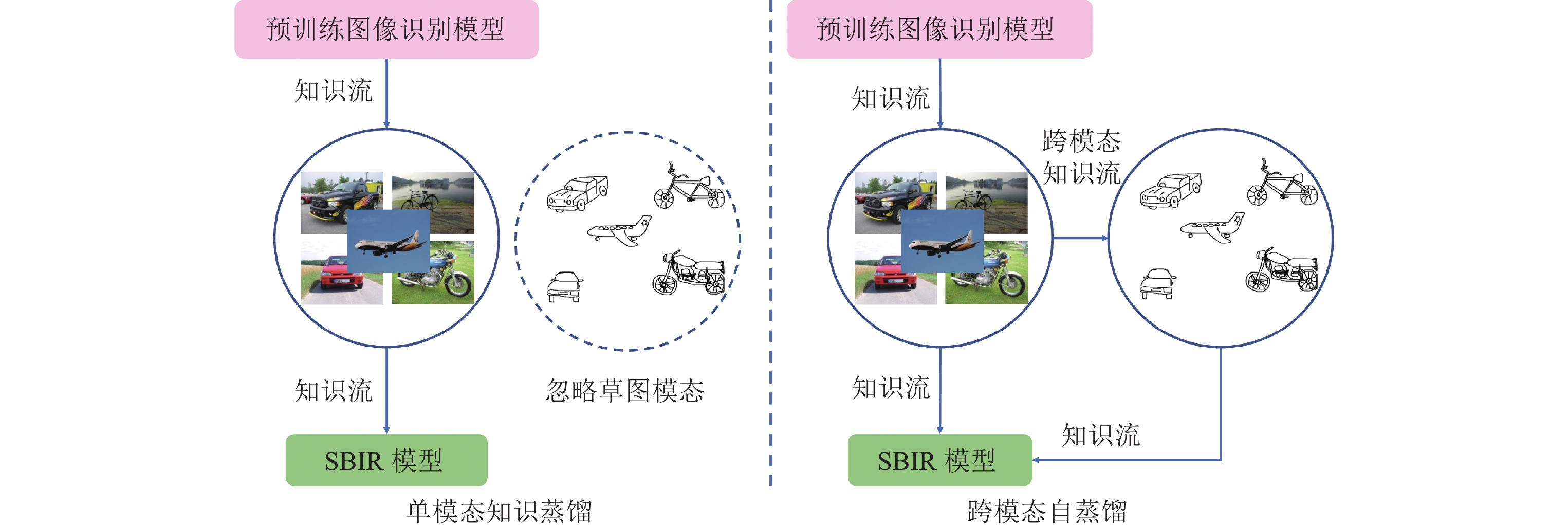
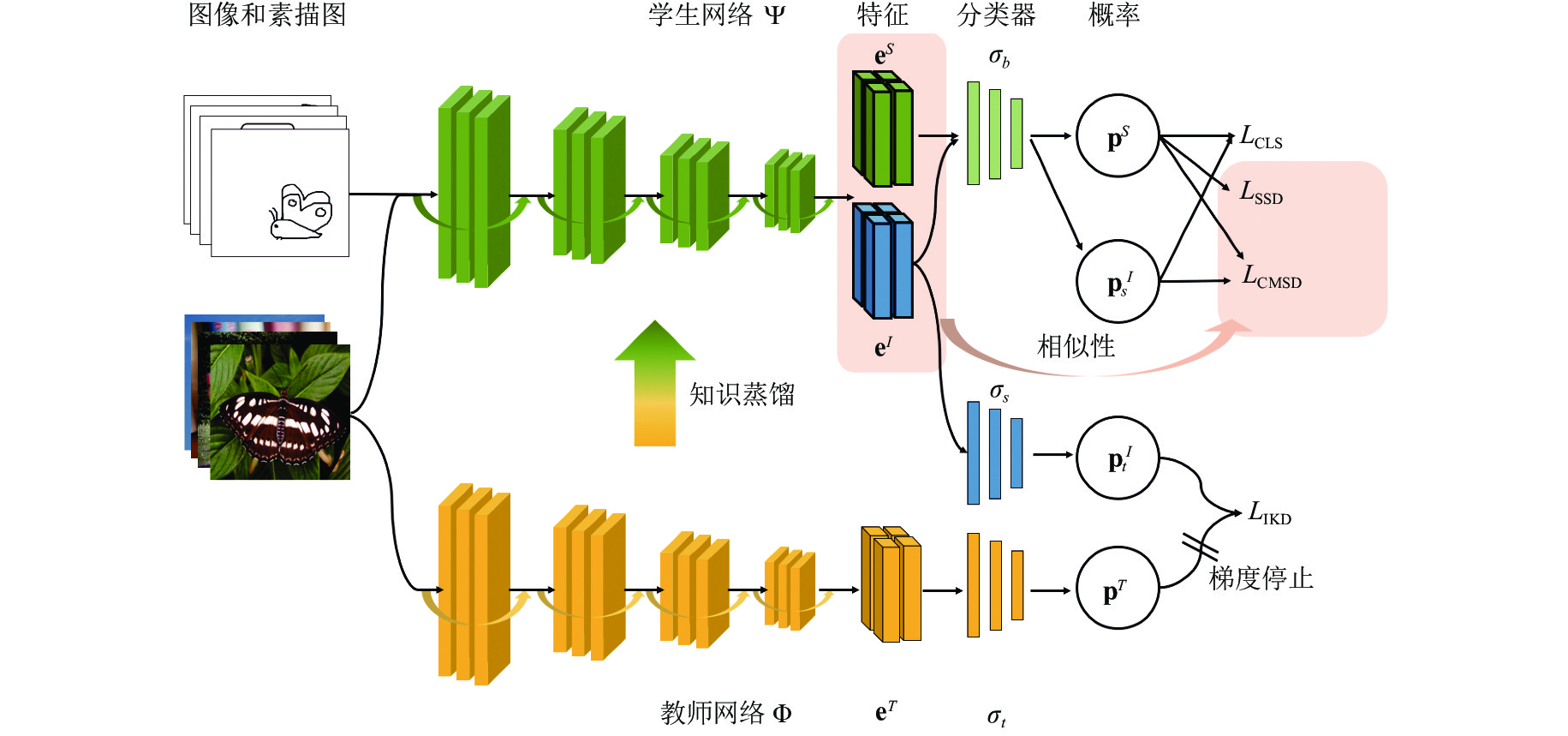
为了解决上述问题, 本文提出了一种新的方法, 即跨模态自蒸馏方法(cross-modal self-distillation, CMSD), 用于零样本草图检索. 本文提出的CMSD方法可以通过跨模态知识迁移而无需语义嵌入来实现超越现有方法的性能. 如图1所示, CMSD方法解决了现有的单模态知识蒸馏的限制, 将知识流通过跨模态迁移从图像模态引入其他模态. 图2展示了CMSD方法的具体流程框架, 在该框架中, 学生网络同时处理图像和草图, 通过特征的相似性和加权概率实现跨模态知识迁移.

为了从图像和草图数据中学习具有判别性、又不失泛化性的特征, 我们从分类和蒸馏两大方面进行模型训练. 首先, 图像和草图必须被正确的分类, 这将保证特征的判别性. 其次, 知识蒸馏将避免训练中的模型迅速地过拟合到特定于模态的信息, 造成预训练知识的遗忘. 我们采用和设计了3种知识蒸馏损失. 第一, 我们通过传统的知识蒸馏损失, 使学生网络模仿教师模型的图像分类能力. 第二, 我们提出跨模态自蒸馏损失. 跨模态自蒸馏利用草图和图像的特征相似度作为桥接模态差异的手段, 以集成和传播的方式, 将教师模型的图像分类知识间接地迁移到草图模态. 具体而言, 我们假设具有相近视觉特征的图像和草图也应该具有一致的分类预测概率; 因而对任意草图样本而言, 其他图像样本的分类预测概率可以加权、集成和传播, 形成软目标(soft target), 作为该草图样本的分类监督信号. 通过优化跨模态自蒸馏损失, 既可以缩小特征的模态差异, 同时还提升模型在零样本场景下的泛化性. 最后, 我们进一步假设特征相近的草图也有上述的性质, 提出草图自蒸馏损失, 使得来自图像模态的知识得到更加有效的利用, 进一步提升特征的判别性和泛化性. 综上, 我们提出的CMSD方法既避免了语义嵌入所带来的资源获取负担, 同时还通过跨模态自蒸馏提升模型在零样本场景下的判别性和泛化性, 并通过大量的实验验证了CMSD的优越性.

综上所述, 本文的贡献有如下3个方面.

(1) 我们提出了一种新颖的ZS-SBIR方法, 简称为CMSD. 该方法关注于视觉样本本身的信息, 不受语义嵌入的资源限制和性能限制.

(2) 我们设计了一种新颖的跨模态自蒸馏损失, 通过跨模态特征相似度, 间接地将教师网络的知识迁移到草图模态, 最终提升模型泛化性和判别性.

(3) 我们进一步提出草图自蒸馏损失, 以特征相似度为权重, 以集成和传播的方式对知识进行加权聚合, 使得知识蒸馏对于ZS-SBIR任务更加有效.

我们在用于ZS-SBIR任务的3个大规模基准数据集Sketchy^[11]、TU-Berlin^[12]和QuickDraw^[8]上, 对本文提出的方法进行了广泛的实验对比和消融分析. 与十几种最先进的方法相比, 我们提出的CMSD方法始终取得了卓越的性能, 证明了本方法中草图自蒸馏和跨模态自蒸馏策略的有效性.

1 相关工作概述

本文研究工作为基于跨模态自蒸馏的零样本草图检索, 属于如下领域的交叉: 基于草图的图像检索(sketch-based image retrieval, SBIR)、零样本学习(zero-shot learning, ZSL)和知识蒸馏(knowledge distillation, KD).

1.1 基于草图的图像检索

SBIR任务不做零样本假设, 只关注模态差异问题. 这个领域的方法可以大致地分为手工特征和深度模型方法. 早期的方法是基于手工特征的^{[13, 14]}, 它们计算图像的边缘图作为图像的替代, 再使用词袋模型抽取边缘图和草图的特征, 以期获得特征的匹配. 当深度学习在识别任务中大获成功之后, 涌现了许多基于深度模型的方法. 其中, 以孪生网络为架构的方法^[15–20]起到了重要作用. 它们以端到端的方式来解决这个问题, 并使用通用的排序损失来训练模型, 如对比损失^[15]、三元组排序损失^[16]和 HOLEF损失^[17].

1.2 零样本学习

ZSL的开创性工作^[21]提出可见类和未见类的概念, 期望模型根据语义特征和可见类的视觉特征进行推理, 并可直接应用于未见类数据的识别问题. 随后的工作大部分是基于投影的框架, 偏重于建立语义特征和视觉特征的联系. 它们要么直接学习从视觉空间到语义空间的映射^[22], 或者反向投影^{[23, 24]}以避免前一种方法带来的枢纽点问题, 又或者学习另一个公共空间^[25]. 最近, 很多工作^[26–28]利用生成模型来合成未见类的特征, 解决单纯的投影所不能处理的领域偏差 (domain bias) 问题, 因而将ZSL问题转化为传统的监督分类问题. 值得说明的是, 所有的ZSL方法都依赖于额外信息, 包括词向量、层次信息和属性向量. 大多数ZS-SBIR方法^[1–3]受此类方法的启发, 选择生成模型作为主体框架, 同样将语义嵌入引入到模型的训练流程中.

1.3 知识蒸馏

知识蒸馏指的是一种训练策略, 其中学生模型学习从预训练的教师网络中提取的各种知识. 这种技术最初应用于模型压缩领域^[29], 此后广泛应用于对抗性防御^[30]和特权学习^[31]等方面. 从训练范式角度看, 教师网络的知识通常为类似概率的“软”标签, 这比通常的“硬”标签包含更多的类间关系. 理论上, 软标签也起到标签平滑和数据增强的作用. 最近, 已经有一些知识蒸馏工作在探索实例之间的关系^[32–34]. 虽然我们提出的草图自蒸馏和跨模态自蒸馏的设计思想是基于特征相似度完成知识的集成和传播, 但也有许多不同之处: 我们专注于研究跨模态数据检索任务, 而不是单模态数据的分类任务; 我们考虑零样本设置下的判别性和泛化性的平衡问题, 提出跨模态蒸馏的知识迁移策略.

1.4 零样本草图检索

ZS-SBIR任务结合SBIR和ZSL任务的特点, 研究如何同时处理草图和图像的模态差异问题以及可见类和未见类的语义不一致性问题. 如前所述, 大多数ZS-SBIR工作选择生成模型作为主体框架, 将语义嵌入引入到框架和损失函数的设计中, 并最终学习一个公共空间作为检索空间. 以生成散列模型^{[1, 35]}, 自动编码器^[5], 变量自动编码器^{[5, 6]}和生成对抗网络^[6]为主要架构的方法是这类方法的典型. Liu等人^[10]从领域适应的角度看待ZS-SBIR任务, 并提出使用知识蒸馏避免灾难性遗忘. 他们中的大多数利用自然语言处理领域的语言模型, 提取词向量^{[1, 6, 8]}, 衡量词相似度, 或结合上述两者^[4]. 尽管Liu等人^[10]首先在ZS-SBIR任务中提出知识蒸馏的训练范式, 但他们的方法仍旧引入了语义嵌入, 且只关注了单模态的蒸馏. 尽管Kiran等人^[5]未引入语义嵌入, 但却没有提出有效的方法去解决语义不一致性, 只实现了相对较差的性能. 我们的方法提出跨模态自蒸馏和草图自蒸馏, 取得了超越现有方法的性能表现.

2 基于跨模态自蒸馏的零样本草图检索 2.1 零样本草图检索定义

我们首先给出零样本草图检索的定义. 零样本草图检索的目的在于, 利用属于可见类的训练数据 (草图和图像) 训练一个模型, 并将其应用于检索属于未见类的草图相关的图像. 因此, 我们可以假定训练集为 ${D_{\text{tr}}} = \{ {I^{\text{seen}}}, {S^{\text{seen}}}\}$ , 其中, ${I^{\text{seen}}} = \{ ({{\mathbf{I}}_i}, {{\mathbf{y}}_i})|{{\mathbf{y}}_i} \in {C^{\text{seen}}}\} _{i = 1}^{{n_1}}$ 和 ${S^{\text{seen}}} = \{ ({s_i}, {{\mathbf{y}}_i})|{{\mathbf{y}}_i} \in {C^{\text{seen}}}\} _{i = 1}^{{n_2}}$ 分别表示草图和图像数据所构成的集合, ${C^{\text{seen}}}$ 为训练阶段所有数据所属类别构成的集合. 同样地, 由未见类 ${C^{\text{un}}}$ 数据所构成的测试集可定义为 ${D_{\text{te}}} = \left\{ {{I^{\text{un}}}, {S^{\text{un}}}} \right\}$ . 在零样本领域, ${C^{\text{seen}}}$ 和 ${C^{\text{un}}}$ 集合之间的交集为空, 即 ${C^{\text{seen}}} \cap {C^{\text{un}}} = \emptyset$ . 由于训练和测试阶段面临的不同类别数据, 本文提出的方法构造各种软标签, 通过知识蒸馏训练模型.

2.2 CMSD总体架构

本文所提出的CMSD模型的总体架构如图2所示. 它包含两个作为特征提取骨架的深度卷积网络 (教师网络 $\Phi $ 和学生网络 $\Psi $ ) 以及3个分类器 ( ${{\mathbf{\sigma }}_b}$ , ${{\mathbf{\sigma }}_s}$ 和 ${{\mathbf{\sigma }}_t}$ ) . $\Phi $ 和 $\Psi $ 在架构上几乎相同, 除了输出层的维度不同. 我们将教师网络和学生网络的输出特征的维度分别记为 ${d_1}$ 和 ${d_2}$ , 因此3个分类器的函数表示分别为如下公式: ${{\mathbf{\sigma }}_b}\left( { \cdot ;{{\mathbf{\theta }}_b}} \right): {\mathbb{R}^{{d_2}}} \mapsto {\{ 0, 1\} ^{\left| {{C^{\text{seen}}}} \right|}}$ , ${{\mathbf{\sigma }}_s}\left( { \cdot ;{{\mathbf{\theta }}_s}} \right):{\mathbb{R}^{{d_2}}} \mapsto {\{ 0, 1\} ^{\left| {{C^{{I}}}} \right|}}$ , 以及 ${{\mathbf{\sigma }}_t}\left( { \cdot ;{{\mathbf{\theta }}_t}} \right):{\mathbb{R}^{{d_1}}} \mapsto {\{ 0, 1\} ^{\left| {{C^{{I}}}} \right|}}$ . 其中, ${C^I}$ 表示ImageNet数据集的类别集合, ${{\mathbf{\theta }}_b}$ 、 ${{\mathbf{\theta }}_s}$ 和 ${{\mathbf{\theta }}_t}$ 分别表示相应分类器的参数. 图像通过学生网络和教师网络获得的特征分别用 ${{\mathbf{e}}^I}$ 和 ${{\mathbf{e}}^T}$ 表示. 草图只输入学生网络, 提取的特征用 ${{\mathbf{e}}^S}$ 表示. 如图2所示, 各个特征经过各个分类器得到相应的分类概率, 分别为 ${{\mathbf{p}}^S}$ , ${\mathbf{p}}_s^I$ , ${\mathbf{p}}_t^I$ 和 ${{\mathbf{p}}^T}$ . 这些符号的上标的意义与特征符号的上标意义相同, 下标用于标识图像的分类概率. 概率向量 ${\mathbf{p}}_s^I$ 的维数为 ${C^{\text{seen}}}$ 的类别数目, 而 ${\mathbf{p}}_t^I$ 的维数是前述 $ \mathcal{C}^I $ 的类别数目 (固定为1000). 前者用于分类和构造草图的跨模态自蒸馏的软目标, 后者用于计算图像知识蒸馏损失.

具体而言, $\Phi $ 和 $\Psi $ 由相同的SE-ResNet-50^[36]初始化 $\Phi $ 和 $\Psi $ 的权重参数, 此外 ${{\mathbf{\sigma }}_t}$ 也初始化为SE-ResNet-50的分类器. 在训练阶段, $\Phi $ 和 ${{\mathbf{\sigma }}_t}$ 的参数不参与更新 (如图2所示“梯度停止”), 只用于监督学生网络 $\Psi $ 及其分类器 ${{\mathbf{\sigma }}_s}$ 的训练过程. 由于学生网络要同时处理草图和图像, 我们在SE-ResNet-50的Squeeze-and-Excitation模块中添加了一个二进制编码, 用于指示输入是图像还是草图. 因此, 也可称特征提取网络为CSE-ResNet-50 (C为conditional的简写). 这样的框架微调有助于消除模态差异, 因为草图和图像的特征提取网络可视为参数共享的孪生网络.

2.3 单模态的图像知识蒸馏

教师网络是在非常大规模的图像数据集(ImageNet)上预训练完成的, 具有强大的辨别能力. 对于一张图像, 教师网络输出的概率向量提供了更加细粒度的语义信息, 而这通常是“硬”标签所包含的. 基于这一观察, Hinton等人^[26]提出, 让学生网络通过匹配教师网络给出的软标签来模仿和学习教师网络的分类能力.

给定一个图片样本 ${I_i}$ , 将其输入 $\Phi $ 和 $\Psi $ , 得到特征嵌入 ${\mathbf{e}}_i^I$ 和 ${\mathbf{e}}_i^I$ ; 再输入分类器 ${{\mathbf{\sigma }}_s}$ 和 ${{\mathbf{\sigma }}_t}$ , 通过Softmax归一化得到概率向量 ${\mathbf{p}}_{t, i}^I$ 和 ${\mathbf{p}}_i^T$ . 知识蒸馏将学生和教师的预测结果之间的KL散度最小化, 使得学生网络模仿教师网络对图像模态的分类能力, 可公式化为如下:

$ {L_{{\rm{IKD}}}} = {D_{{\rm{KL}}}}({\mathbf{p}}_i^T|{\mathbf{p}}_{t, i}^I) $

(1)

公式(1)大体类同传统的知识蒸馏方法, 借助于在大规模图像数据集上预训练的深度卷积网络, 再结合分类损失, 驱使学生网络不仅能在训练集上学习到具有判别性的特征, 还能保留从大规模数据集中学习得到的知识, 从而使特征具有泛化性, 有助于消弭零样本设置下的语义不一致. 然而, 上述方法缺陷也很明显, 即需要预训练的深度卷积网络. 由于缺乏在大规模草图数据集上预训练的深度卷积网络, 因此无法应用于草图模态, 难以消弭多模态任务所面临的模态差异.

2.4 跨模态自蒸馏

为了解决上述模态差异问题, 本文提出跨模态自蒸馏解决此问题, 无需草图模态的预训练网络, 只需通过模态内和模态间的自蒸馏, 完成知识的二次迁移: 将图像模态的预训练模型的图像分类能力迁移为学生模型的图像分类能力, 再迁移为学生模型的草图分类能力. 通过知识的二次迁移, 学生模型在图像和草图两个模态上都得到监督引导, 同时消弭了模态差异和语义差异, 使得学生模型在零样本跨模态任务中表现更好.

图像和草图模态间的知识集成和传播, 即为前述跨模态自蒸馏. 给定任意一批样本, 假设图像和草图数目分别为 $ N_{1} $ 和 ${N}_{2}$ , 对应的特征嵌入矩阵表示为 ${{\mathbf{E}}^I} = {\left[ {{\mathbf{e}}_1^I, {\mathbf{e}}_2^I, \ldots , {\mathbf{e}}_{{N_1}}^I} \right]^{\rm{T}}}$ 和 ${{\mathbf{E}}^I} = {\left[ {{\mathbf{e}}_1^S, {\mathbf{e}}_2^S, \ldots , {\mathbf{e}}_{{N_1}}^S} \right]^{\rm{T}}}$ , 对应的概率矩阵表示为 ${{\mathbf{P}}^I} = {\left[ {{\mathbf{p}}_{s, 1}^I, {\mathbf{p}}_{s, 2}^I, \ldots , {\mathbf{p}}_{s, {N_1}}^I} \right]^{\rm{T}}}$ 和 ${{\mathbf{P}}^S} = {\left[ {{\mathbf{p}}_1^S, {\mathbf{p}}_2^S, \ldots , {\mathbf{p}}_{{N_2}}^S} \right]^{\rm{T}}}$ , 其中 ${\mathbf{p}}_{s, i}^I$ 和 ${\mathbf{p}}_i^S$ 是通过带温度超参数 $\tau $ 的Softmax归一化得到的向量. 不失一般性地, ${\mathbf{p}}_i^S$ 的计算公式为:

$ {\mathbf{p}}_i^S = \frac{{\exp \left( {{\sigma _b}\left( {{\mathbf{e}}_i^S} \right)/\tau } \right)}}{{\displaystyle\sum\limits_{i = 1}^{|{C^{{\rm{seen}}}}|} {\exp } \left( {{\sigma _b}\left( {{\mathbf{e}}_i^S} \right)/\tau } \right)}} $

(2)

然后, 以余弦相似度为距离度量, 计算草图和图像特征的成对相似度, 构成相似矩阵 ${\mathbf{R}} \in {\mathbb{R}^{{N_1} \times {N_2}}}$ :

$ {{\mathbf{R}}_{i, j}} = \frac{{{{\left( {{\mathbf{e}}_i^S} \right)}^T} \cdot {\mathbf{e}}_j^I}}{{\left\| {{\mathbf{e}}_i^S} \right\| \cdot \left\| {{\mathbf{e}}_j^I} \right\|}}) $

(3)

接着, 将相似矩阵 ${\mathbf{R}}$ 的每一行进行归一化, 使得 ${\mathbf{R}}$ 的行和都为1, 记为 $\widehat {\mathbf{R}}$ , 即 $\displaystyle\sum\limits_j {{{\widehat {\mathbf{R}}}_{i, j}}} = 1$ :

$ \widehat{\mathbf{R}}_{i, j}=\frac{\exp \left(\mathbf{R}_{i, j}\right)}{\displaystyle\sum_{j} \exp (\mathbf{R}_{i, j})} $

(4)

对于任意草图样本, 可根据相似矩阵 ${\mathbf{R}}$ 加权集成图像样本的分类预测概率, 以形成草图的自蒸馏软目标, $\widehat {\mathbf{p}}_i^S = \displaystyle\sum\limits_j {{{\widehat {\mathbf{R}}}_{i, j}}} {\mathbf{p}}_{s, j}^I$ . 因此, 当草图和图像的特征近似时, ${{\mathbf{R}}_{i, j}}$ 接近于1, $\widehat {\mathbf{p}}_i^S$ 也更接近于 ${\mathbf{p}}_{s, j}^I$ . 然而, 单纯加权图像的分类预测概率, 也难以避免噪声和训练的不稳定性. 因此, 软目标可定为 $\displaystyle\sum\limits_{j \ne i} {{{\widehat {\mathbf{R}}}_{i, j}}} {\mathbf{p}}_{s, j}^I$ 和 ${\mathbf{p}}_i^S$ 的滑动平均, 则最终的软目标可公式化如下:

$ \widehat {\mathbf{p}}_i^{{S}} = \omega \cdot \sum\limits_j {{{\widehat {\mathbf{R}}}_{i, j}}} {\mathbf{p}}_{s, j}^I + (1 - \omega ) \cdot {\mathbf{p}}_i^S $

(5)

其中, $\omega $ 为滑动平均的加权系数. 因此, 跨模态自蒸馏损失为:

$ {L_{\rm{CMSD}}} = {\tau ^2} \cdot {D_{{\text{KL}}}}\left( {\widehat {\mathbf{p}}_i^S\mid {\mathbf{p}}_i^S} \right) $

(6)

2.5 单模态的草图自蒸馏

跨模态自蒸馏通过特征相似矩阵将草图和图像两个模态联系起来, 进而将草图模态和预训练模型联系起来, 完成知识从图像模态到草图模态的迁移. 我们进一步地提出草图自蒸馏损失, 目的在于将学到的知识在每一批草图样本中传播, 提升知识迁移的有效性.

类似地, 草图特征的成对相似度可定义为如下:

$ {\mathbf{R}}_{i, j}^S = \frac{{{{\left( {{\mathbf{e}}_i^S} \right)}^T} \cdot {\mathbf{e}}_j^S}}{{\left\| {{\mathbf{e}}_i^S} \right\| \cdot \left\| {{\mathbf{e}}_j^S} \right\|}} $

(7)

与前述跨模态自蒸馏一样做归一化:

$ \widetilde {\mathbf{R}}_{i, j}^S = \frac{{{\mathbf{1}_{i \ne j}} \cdot \exp \left( {{\mathbf{R}}_{i, j}^S} \right)}}{{\displaystyle\sum\limits_j {{ \mathbf{1}_{i \ne j}}} \cdot \exp \left( {{\mathbf{R}}_{i, j}^S} \right)}} $

(8)

其中, 当 $i \ne j$ 为真时 ${{\mathbf{1}}_{i \ne j}}$ 为1, 否则为0. 值得注意的是, 我们用 ${{\mathbf{1}}_{i \ne j}}$ 排除样本的自我比较情况, 以免影响该样本和其他样本的比较强度. 经滑动平均后得到的软目标为:

$ \widetilde {\mathbf{p}}_i^{{S}} = \omega \cdot \sum\limits_j {\widetilde {\mathbf{R}}_{i, j}^S} {\mathbf{p}}_j^S + (1 - \omega ) \cdot {\mathbf{p}}_i^S $

(9)

其中, $\omega $ 为滑动平均的加权系数. 由于公式(8)中的 ${\widetilde {\mathbf{R}}^S}$ 为对称方阵(当 ${N_1}$ 和 ${N_2}$ 不相等时, 公式(4)中的 $\widehat {\mathbf{R}}$ 不为方阵), 可重复迭代公式(9)直至收敛, 可由矩阵形式解析解计算:

$ \widetilde {\mathbf{P}}_{(\infty )}^S = (1 - \omega ){\left( {I - \omega {{\widetilde {\mathbf{R}}}^S}} \right)^{ - 1}}{{\mathbf{P}}^S} $

(10)

因此, 草图自蒸馏损失可定义为如下:

$ {L_{\rm{SSD}}} = {\tau ^2} \cdot {D_{{\text{KL}}}}\left( {\widetilde {\mathbf{p}}_{(\infty ), i}^S\mid {\mathbf{p}}_i^S} \right) $

(11)

2.6 总体目标函数

综合公式(1)、公式(6)和公式(11), 以及草图和图像的交叉熵分类损失, 得到总体目标函数为:

$ L = {\lambda _1}{L_{\rm{IKD}}} + {\lambda _2}{L_{\rm{CMSD}}} + {\lambda _3}{L_{\rm{SSD}}} + {\lambda _4}{L_{\rm{CLS}}} $

(12)

其中, ${\lambda _1}$ 、 ${\lambda _2}$ 、 ${\lambda _3}$ 和 ${\lambda _4}$ 为加权参数, ${L_{\rm{CLS}}}$ 为交叉熵分类损失. 对于图像模态, 其优化目标函数为:

$ {L_{\rm{IMG}}} = {\lambda _1}{L_{\rm{IKD}}} + {\lambda _4}{L_{\rm{CLS}}} $

(13)

对于草图模态, 其优化目标函数为:

$ {L_{\rm{SKT}}} = {\lambda _2}{L_{\rm{CMSD}}} + {\lambda _3}{L_{\rm{SSD}}} + {\lambda _4}{L_{\rm{CLS}}} $

(14)

2.7 优化过程

训练时, 同时采样草图和图像, 每批样本由 ${N_1}$ 张图像和 ${N_2}$ 张草图组成. ${N_1}$ 和 ${N_2}$ 的比例视数据集的情况而定: 对于图像和草图数量平衡的Sketchy和QuickDraw, 我们将 ${N_1}$ 和 ${N_2}$ 的比例设为2:1; 对于图像和草图数量极端不平衡的TU-Berlin, 我们将比例设为8:1. 这样的设置使得学生模型逐步学习草图的特征, 而不至于快速过拟合到特定于模态、特定于类别的状态, 从而提高模态的泛化性. 在实际优化过程中, 我们采用随机梯度下降对公式(12)(公式(13)和公式(14)之和)优化学生网络 $\Psi $ 以及分类器 ${\sigma _b}$ 和 ${\sigma _s}$ 的参数:

$ {\theta _\Psi },{\theta _{{\sigma _b}}},{\theta _{{\sigma _s}}} = {{\mathop{\rm arg\;\min}\nolimits} _{{\theta _\psi },{\theta _{{\sigma _b}}},{\theta _{{\theta _s}}}}}{\lambda _1}{L_{\rm{IKD}}} + {\lambda _2}{L_{\rm{CMSD}}} + {\lambda _3}{L_{\rm{SSD}}} + {\lambda _4}{L_{\rm{CLS}}} $

(15)

模型收敛时, 停止优化过程. 学生网络的 ${\theta _\Psi }$ 最终用于提取未见类图像和草图的特征, 实现最后的检索.

3 实验结果与分析 3.1 数据集

3个ZS-SBIR基准数据集用于度量我们提出的方法, 包括Sketchy^[11]、TU-Berlin^[12]和QuickDraw^[8]. 原始的Sketchy数据集由125类别构成, 包含12 500张自然图像和75 471张草图. Liu等人^[8]对图像集合进行拓展, 最终得到包含73 002张图像的集合. 这个数据集有两种训练和测试数据的划分方法: 一种随机选择25个类别作为未见类(Shen等人^[1]); 另一种固定选择21个类别(Kiran等人^[5]), 这些类别确保与ImageNet类别集合没有交集. 我们在两种设置下都进行了实验.

TU-Berlin数据集^[12]由250个类别构成, 包含20 000张草图和204 489张自然图像. 正如草图数量只有图像的1/10, 它存在草图和图像数量的极端不平衡, 使得模型在这个数据集上优化更加困难. 我们依照Shen等人^[1]提出的划分方式, 随机选择30个类作为未见类.

QuickDraw数据集^[8]是3个数据集中最大的数据集, 由110个类别构成, 但包含了总共33万张草图和20.4万张图片. 另外, 这个数据集所包含的草图内容最抽象, 来源于业余用户的手绘, 而非专业人员的绘画. 同样地, 这个数据集划分出30个类别作为未见类, 并严格保证它们与ImageNet类别没有交集. 因此, 这个数据集也是3个数据集中最具有挑战性的数据集.

3.2 实现细节

我们的实验代码使用PyTorch实现, 在两块RTX2080Ti GPU上进行模型的训练. 我们选择Adam优化器作为模型的优化方法. 各损失函数加权系数 ${\lambda _1}$ 、 ${\lambda _2}$ 、 ${\lambda _3}$ 和 ${\lambda _4}$ 分别设为1, 0.1, 0.1和1. 一批图像的数量 $ N_{1} $ 被设置为64, ${N_2}$ 按照前述比例进行设置. 学习率初始为1E–4, 在训练过程中以指数衰减的方式降低到1E–6. 蒸馏的温度超参数保持 $\tau = 0.1$ . 滑动平均系数 $\omega $ 设为0.5. 此外, 在训练期间周期性地冻结批量归一化层对算法的性能有提升作用. 为了公平比较, 我们采用前人提出的评价指标^{[6, 7]}, 包括均值评价精度(mAP@k)和准确率(Prec@k), 其中k表示前k个查询结果. 为未见类草图和图像提取特征后, 我们采用余弦相似性作为距离度量来进行检索.

3.3 与现有方法的比较

我们将提出的CMSD与8个现有的ZS-SBIR工作进行了比较: ZSIH^[1], CAAE和CVAE^[5], SEM-PCYC^[4], Dey等人^[8], SAKE^[10], LCALE^[6], OCEAN^[7]. 我们按照有无使用语义嵌入来分类这些方法. 其中, 除CAAE和CVAE外, 其余的算法都将语义嵌入引入至框架或损失函数的设计中. 为了更清楚地分析我们提出的方法的优越性, 我们根据SAKE的代码重新训练出无语义嵌入参与的模型, 并将其命名为SAKE w/o s. 此外, 我们还分别将SBIR和ZSL领域的两篇论文纳入比较(GN-Triplet^[16]和DSH^[11], 以及SAE^[37]和ZSH^[38]), 以分析ZS-SBIR方法在零样本和跨模态设置下的优越性.

在Sketchy和TU-Berlin数据集上的实验结果见表1, 在QuickDraw数据集上的实验结果见表2. 我们首先比较无语义嵌入参与训练的方法, 这包含SBIR方法和一些ZS-SBIR方法. 从表1可以观察到, 除了CAAE在Sketchy上表现不加, SBIR方法的整体表现远远不如ZS-SBIR方法的整体表现. 原因在于SBIR方法只考虑了训练数据的分布, 而没考虑模型在未见类数据上的迁移性. 比较ZS-SBIR方法, 综合表1和表2可知, CAAE和CVAE表现不佳, 我们提出的CMSD在所有实验设置下都取得了最好的结果. 以mAP指标为例, 我们在Sketchy上比SAKE (w/o s)高出0.08, 在Skethcy (split 2)上高出0.023, 在TU-Berlin上高出0.027, 在QuickDraw高出0.021. 这样一致且显著的提升证明CMSD能通过跨模态自蒸馏有效地完成知识迁移, 使得CMSD无需语义嵌入就能取得最好的结果. 而CAAE和CVAE都是生成式方法, 在没有将语义嵌入引入模型训练时, 很难实现将模型泛化至未见类的草图检索. SAKE也是从知识蒸馏角度看待零样本草图检索任务, 然而它在取消语义嵌入后依旧出现了性能下降. 这进一步说明了我们方法的有效性.

接着, 我们将CMSD和使用语义嵌入的那一类方法进行比较, 它们属于ZSL和ZS-SBIR领域. 类似地, ZSL方法的整体性能表现不如ZS-SBIR, 因为它们并没有考虑多模态数据所面临的模态差异问题, 使得学习得到的特征依据保留较大的模态差异. 在ZS-SBIR方法中, CMSD依旧表现出了一致且显著的提升, 超越了所有的现有方法. 因此, 这证明了CMSD无需语义嵌入也能同时处理模态差异和语义不一致问题.

综上实验观察, 我们可以得出结论, CMSD在零样本草图检索任务上表现优异, 既减轻了对训练资源的需求, 也改善了现有方法在模型泛化性方面的不足, 提出的跨模态自蒸馏在解决模态差异和语义不一致性方面的价值.

3.4 CMSD消融分析

我们通过消减相应的损失项来分析它们(包括跨模态自蒸馏CMSD、草图自蒸馏SSD、图像知识蒸馏IKD和分类CLS)的效果. 我们选择Sketchy和TU-Berlin数据集做实验, 并在表3中显示了消融的模型. 这些模型的编号从模型1到模型7. 模型1集成了所有损失项, 这是我们提出的方法. 模型2、3、4和5可以归为一类: 上述4个组件中的一个没有参与模型的训练和优化. 没有跨模态自蒸馏和草图自蒸馏的消融模型被称为模型6. 我们进一步消减了所有的知识蒸馏组件, 并将其命名为模型7.

消融结果见表3. 通过比较这些模型的实验结果, 我们可以得出以下结论: 1) 图像知识蒸馏是3个蒸馏损失项中最重要的, 它的消融将导致性能的明显下降, 这在模型2、3、4的比较中得到了体现. 2) 尽管跨模态自蒸馏和草图自蒸馏的重要性不如图像知识蒸馏, 但它们与图像知识蒸馏集合后可以显著提高模型的性能, 这可以在模型3和6、模型4与6的比较中观察到. 3) 与模型7相比, 跨模态自蒸馏和草图自蒸馏的组合(模型4)也取得了改善, 这表明跨模态自蒸馏和草图自蒸馏能有效地将知识从教师模型迁移到学生模型. 4) 模型5的性能严重退化, 因为在消减分类损失后, 模态差距很难缩小. 5) 模型7的性能明显下降, 因为所有的知识蒸馏损失在训练过程中不包括在内, 导致检索未见类的样本所需的泛化能力严重下降. 6) 在集成所有损失时, 我们的方法(模型1)同时利用知识蒸馏和分类得到超过所有变体的结果.

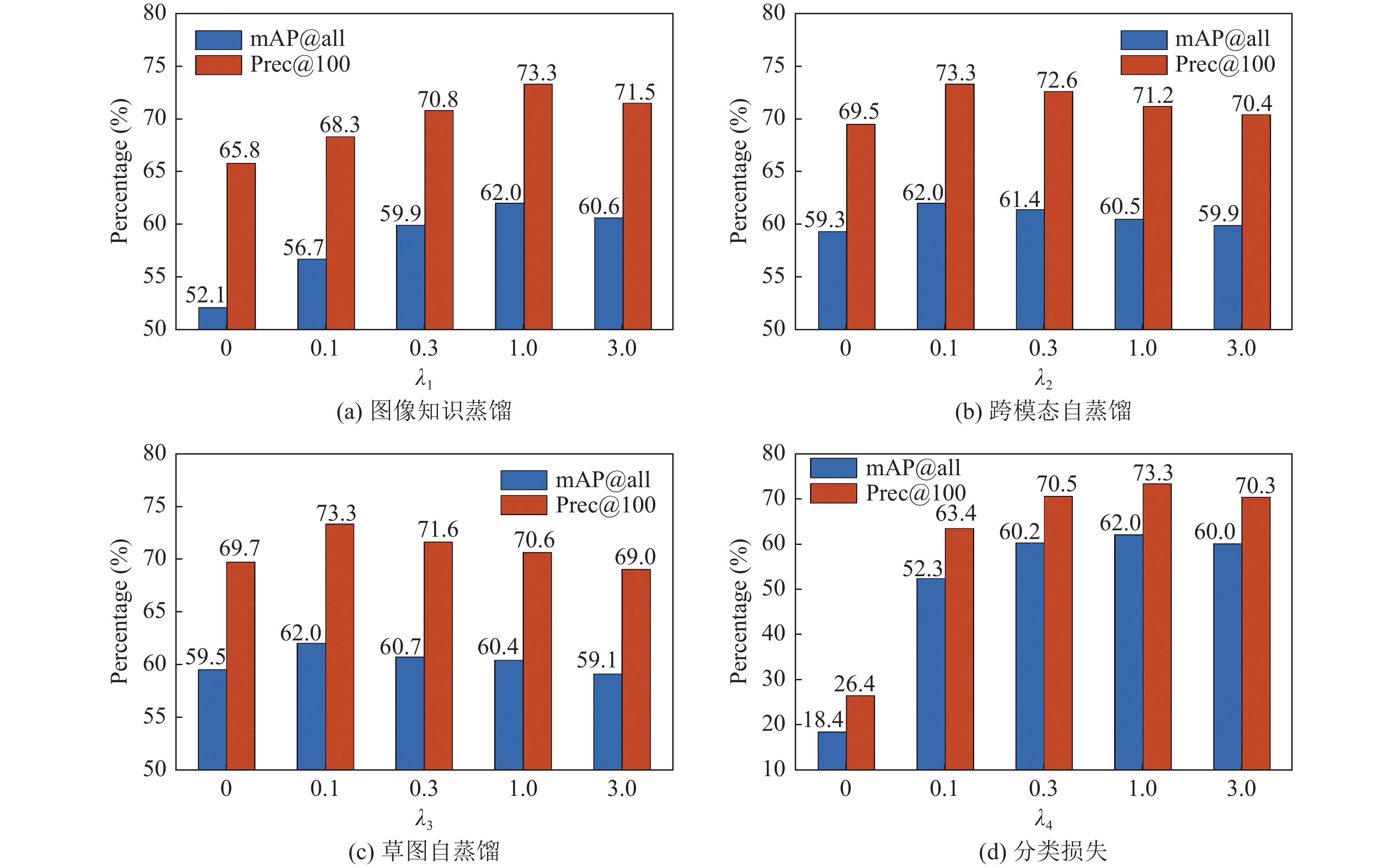
3.5 CMSD参数分析

在这个实验中, 我们通过改变Sketchy上的 ${\lambda _1}$ 、 ${\lambda _2}$ 、 ${\lambda _3}$ 和 ${\lambda _4}$ 的值进行了参数分析. 我们将这些系数的范围设定为[0.0, 3.0], 并在图3中显示了结果. 我们可以观察到, 性能曲线在 ${\lambda _2}$ 、 ${\lambda _3}$ 为0.1时达到峰值, 在 ${\lambda _1}$ 和 ${\lambda _4}$ 为1时达到峰值. 当这些系数的值过大或过小时, 性能不可避免地会下降. 这可能是因为当这些系数小的时候, 训练过程对某一项组件关注过少, 影响了知识蒸馏的有效性; 而当它们太大时, 训练过程则对某一组件关注过多, 增加了优化的不稳定性. 因此, 适当加权有利于总体性能的提高.

3.6 定性实验

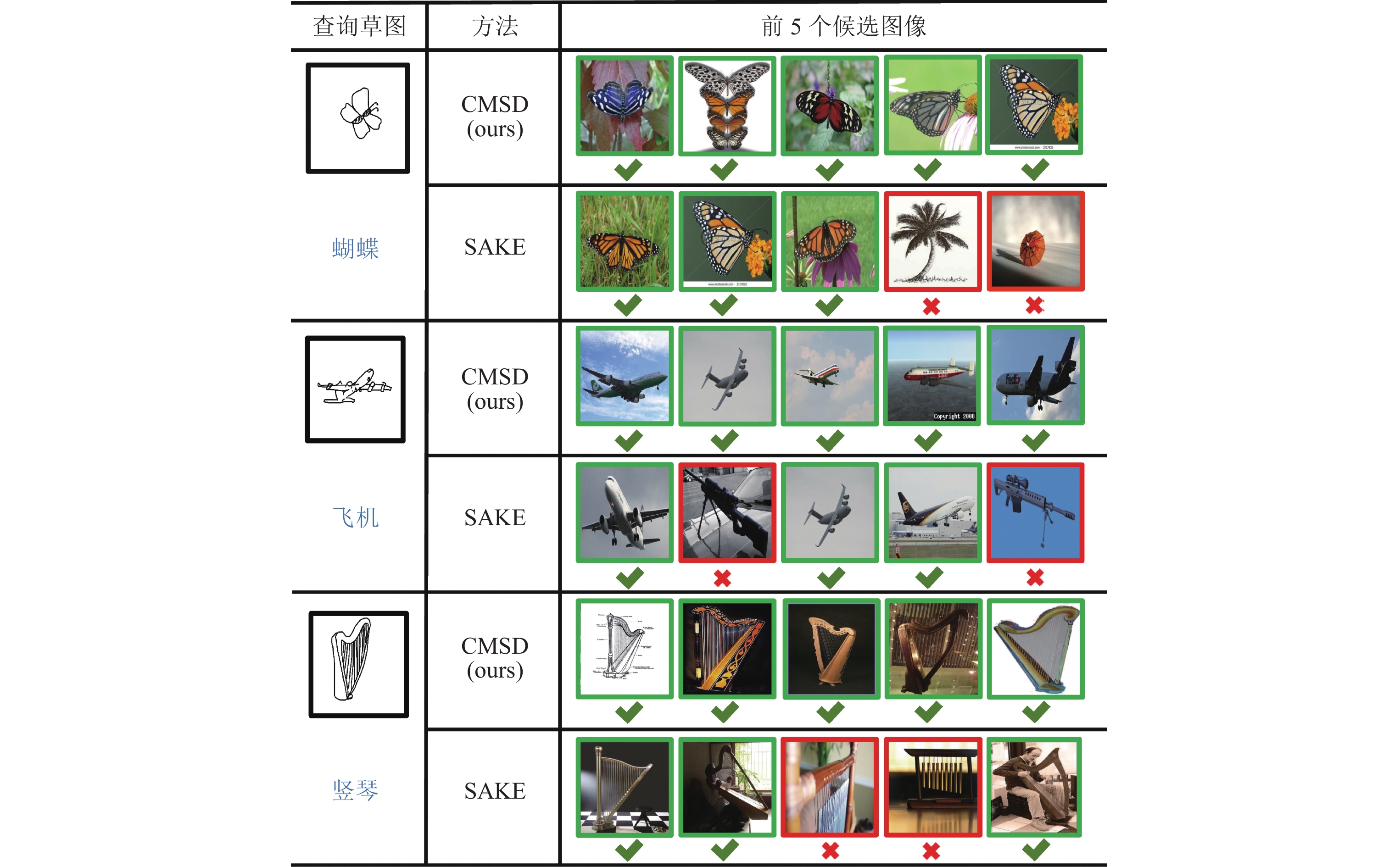
我们展示了CMSD在Sketchy上的可视化结果, 并在图4中与SAKE做了定性比较, 其中, 最左边的草图代表查询样本和它们的类别标签, 右边是正确的和错误的候选者, 分别用绿色的外框线和红色的叉号标记. 通过比较, 发现我们的模型可以成功地检索到与查询草图的相同类别的图像, 但SAKE的检索结果却有些错误. 通过观察检索结果, 我们还发现, 我们模型的检索能力是基于草图和图像中的视觉信息的, 即查询草图和候选图像在形状和结构模式上非常相似. 这样的结果在某种程度上是合理的: 草图是高度抽象的, 主要描绘物体的外观结构, 略去了细粒度的细节和复杂的背景, 这导致物体结构相似的图像更容易被检索.

4 结　论

本文提出了一种新颖的跨模态自蒸馏模型来解决零样本草图检索问题, 并在没有语义嵌入的情况下实现最好的性能. 一方面, 我们提出了跨模态自蒸馏损失, 使知识从预训练的图像识别模型流向草图模态. 另一方面, 我们进一步提出草图自蒸馏损失, 以集成和传播的方式使得知识在草图模态内得到更有效的利用. 在3个ZS-SBIR基准数据集上的广泛比较结果证明了我们模型的有效性. 消融实验和参数分析实验证明我们方法有效地完成知识迁移, 解决零样本草图检索所面临的模态差异问题和语义不一致性问题. 我们将在未来的工作中探索更有效的解决方案, 以最大限度地减少模态差异和语义不一致.