2. 交通数据分析与挖掘北京市重点实验室(北京交通大学), 北京 100044
2. Beijing Key Lab of Traffic Data Analysis and Mining (Beijing Jiaotong University), Beijing 100044, China
时间序列数据广泛存在于现实世界的各个领域, 目前对时间序列的分析已经成为股票价格、天气数据、生物医学测量、航空航天等许多领域研究的重要课题[1, 2]. 时间序列数据类型为实值型, 数据维度高且数据量通常较大. 此外, 时间序列分类问题中的序列属性是有序的, 这使其明显区别于传统的分类问题. 实质上, 序列中的属性排序是否按照时间进行是无关紧要的, 重要的是序列中可能存在依赖于顺序的辨别性特征[3]. 因此, 时间序列分类问题的研究对于数据挖掘领域的发展具有重要意义.
在时间序列分类问题中, 最近邻算法(one nearest neighbor, 1NN)是目前最为流行的分类算法之一, 该算法较为简单, 且分类效果显著. 最近邻算法的核心部分就是相似性度量, 而动态时间规整(dynamic time warping, DTW)就是一种非常有效的相似性度量算法, 该算法能够通过局部的非线性规整找到序列间的最佳匹配路径. DTW是由Berndt等人[4]提出并将其应用到了时间序列的模式发现, 后来又被广泛用于人体活动识别[5], 孤立词识别[6], 文字图像匹配[7], 人体运动动画[8], 生物信息处理[9]以及时间序列分类[3]等多个领域中.
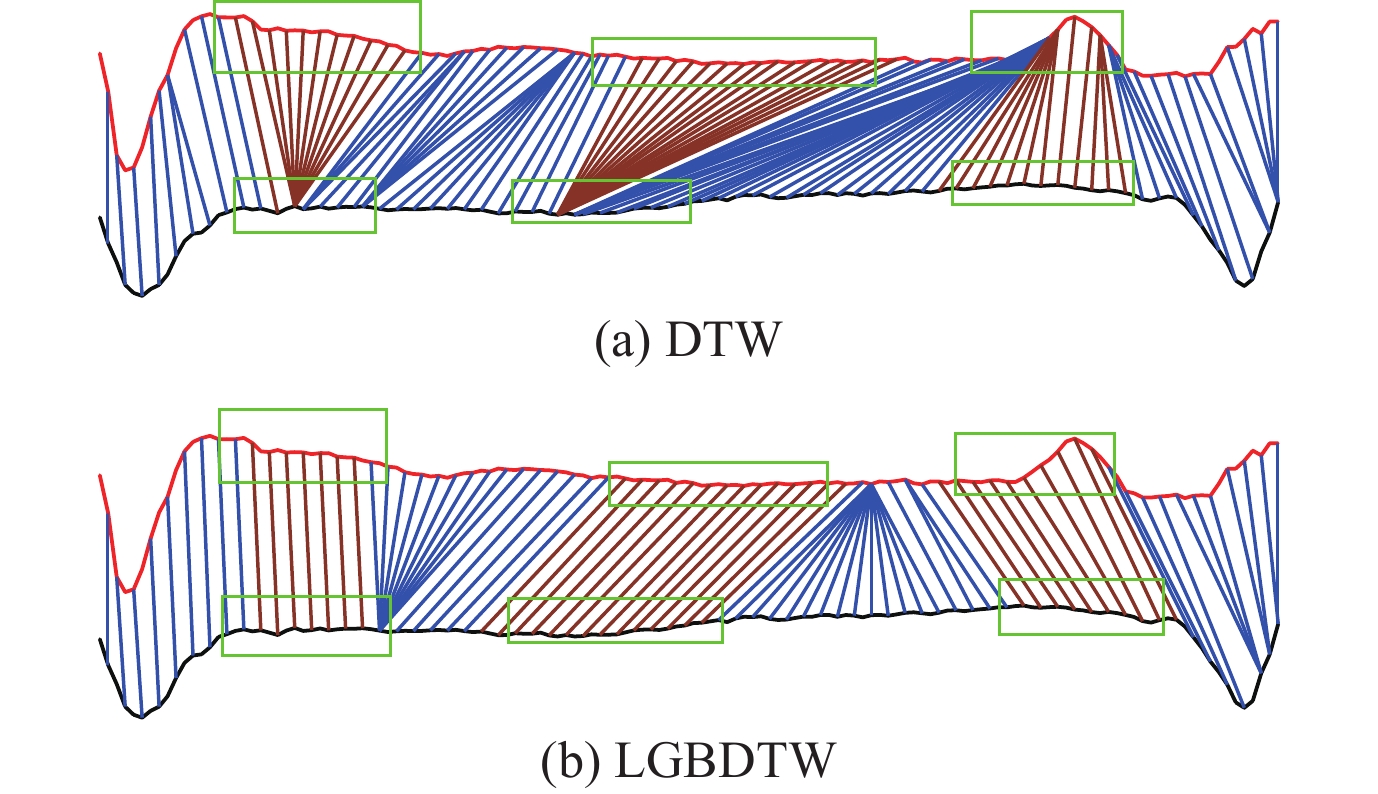
基于DTW的1NN算法是众多时间序列分类算法中最有效的算法之一, 很难被其他算法超越[3]. DTW本质上是一种点对点的对齐算法, 它通过允许一个序列到另一个序列的非线性映射提高了匹配点对之间的时间一致性. 从DTW提取匹配分量之后, 通常是基于两点之间的欧几里得距离来进行点匹配. 然而, 这种使用基于点数值的欧几里得距离的相似性度量方法是不可靠的, 甚至会导致匹配错误, 即产生局部结构并不相似的点的对齐(如图1(a)所示). 很明显, 虽然DTW实现了全局最优匹配, 但它没有兼顾序列的局部结构信息. 这也反映了为什么DTW相似性度量之下的最近邻分类器的可解释性会弱于基于shapelet的分类器[10, 11]. 总的来说, DTW的确能够捕捉到时间序列的全局最优匹配, 但是它没有考虑到序列的局部结构信息, 这样的对齐结果是缺乏语义的.
|
Fig. 1 Comparison of alignment effect between DTW and LGBDTW 图 1 DTW与LGBDTW对齐效果比较 |
为了解决这个问题, 本文提出了一种基于局部梯度和局部二进制模式(local binary pattern, LBP)的动态时间规整算法LGBDTW. 该算法不只是考虑了时间序列点的局部梯度信息, 同时还兼顾点的局部二进制模式信息, 它通过将点对的这两种局部结构信息以一定的权重进行融合强化了DTW. 通过实例测试, 所提算法获得了更加准确并具有较好可解释性的对齐. 图1(b)是一个基于LGBDTW对齐的实例, 很明显时间序列间的局部形状信息被成功匹配.
本文所提出方法的灵感来自于计算机视觉领域的方向梯度直方图(histogram of oriented gridients, HOG)[12], 图像特征描述子LBP[13], 以及一维时间序列局部特征描述子HOG-1D[11]. 众所周知, 现实世界大多数数据可能含有噪声, 时间序列数据也是如此, 其获取甚至分类过程很容易受到噪声的影响. 因此, 本文首先使用滤波技术来缓解噪声对数据的影响, 然后提出了一种基于局部二进制模式的时间序列局部特征描述子LBPT (local binary pattern of time series), 之后又在此基础上提出了融合HOG-1D和LBPT两种特征描述子的加权动态时间规整算法(LGBDTW), 并成功将其应用到了时间序列分类任务.
本文的主要贡献如下: (1)提出了一种新的基于局部二进制模式的时间序列局部特征描述子LBPT来更加准确的反映序列的局部结构信息. (2)提出了一种基于HOG-1D特征描述子和LBPT特征描述子的加权动态时间规整算法. (3)所提出的分类算法应用到真实数据集中明显提高了分类准确率, 并且具有较好的可解释性.
本文第1节介绍了时间序列分类, 动态时间规整算法以及局部特征提取的相关工作. 在第2节和第3节介绍本文提出的算法. 然后在第4节给出了实验结果分析. 最后, 在第5节进行相应总结并简单探讨未来的研究方向.
1 相关研究工作随着时间序列分类问题在各个领域的重要性日益提高, 人们提出了许多适合不同应用的时间序列分类算法. 这些算法主要可以分为基于距离的和基于特征的两种类型. 前者是将最近邻分类器与不同的距离度量算法相结合, 比较典型的有时间扭曲编辑(TWE)[14]、移动-分割-合并(MSM)[15]等. 后者是在原始序列中提取具有辨别性的特征, 以此将原始序列转换到新的特征空间. 比较常见的有时间序列森林(TSF)[16]、时间序列特征包(TSBF)[17]、shapelets转换[10]、学习模式相似性(LPS)[18]、符号聚合近似(SAX)[19]、以及模式包(BOP)[20]等. 此外, 一些研究者还将不可预测的卷积神经网络(CNN)应用到了时间序列分类问题的特征提取中. 例如, Le Guennec等人[21]将CNN扩展到了时间序列分类问题, 提出了时间LeNet (t-LeNet); Cui等人[22]提出了一种多尺度CNN方法 (MCNN), 它基于提取的子序列来训练CNN; Wang等人[23]还将多层感知机(MLP)、全卷积神经网络(FCN)和残差网络(ResNet)成功地应用于时间序列. 此外, Zhao等人[24]提出了时间CNN (Time-CNN)算法, 用均方误差代替交叉熵损失函数来兼容时间序列. 然而, 这类引入神经网络的方法往往复杂度过高, 同时其结果是缺乏可解释性的.
在时间序列分类问题中, DTW是一种非常经典的相似性度量算法, 发展到现在已经有了很多关于它的改进算法. 对于该算法匹配路径过于扭曲的问题, 传统来讲, 可以通过添加一些约束来缓解, 例如Sakoe-Chiba band[6]、局部相关约束[25]以及有限扭曲路径长度[26]等. 此外, 一些研究者试图通过加入权重或利用导数等信息来改善序列对齐质量. 例如, Keogh等人[27]提出了基于导数的动态时间规整(DDTW); Jeong等人[28]提出了一种基于惩罚的加权动态时间规整(WDTW)算法; 此外, 一种复杂性-不变DTW (CID)被Gustavo等人[29]提了出来, 这种方法通过乘以复杂性校正因子弥补了被比较序列之间的复杂性. 然而, 在这些方法中, 时间点的相似性都是依赖单一点的数值或其衍生值来度量的, 这些度量方式忽略了序列点的局部结构信息.
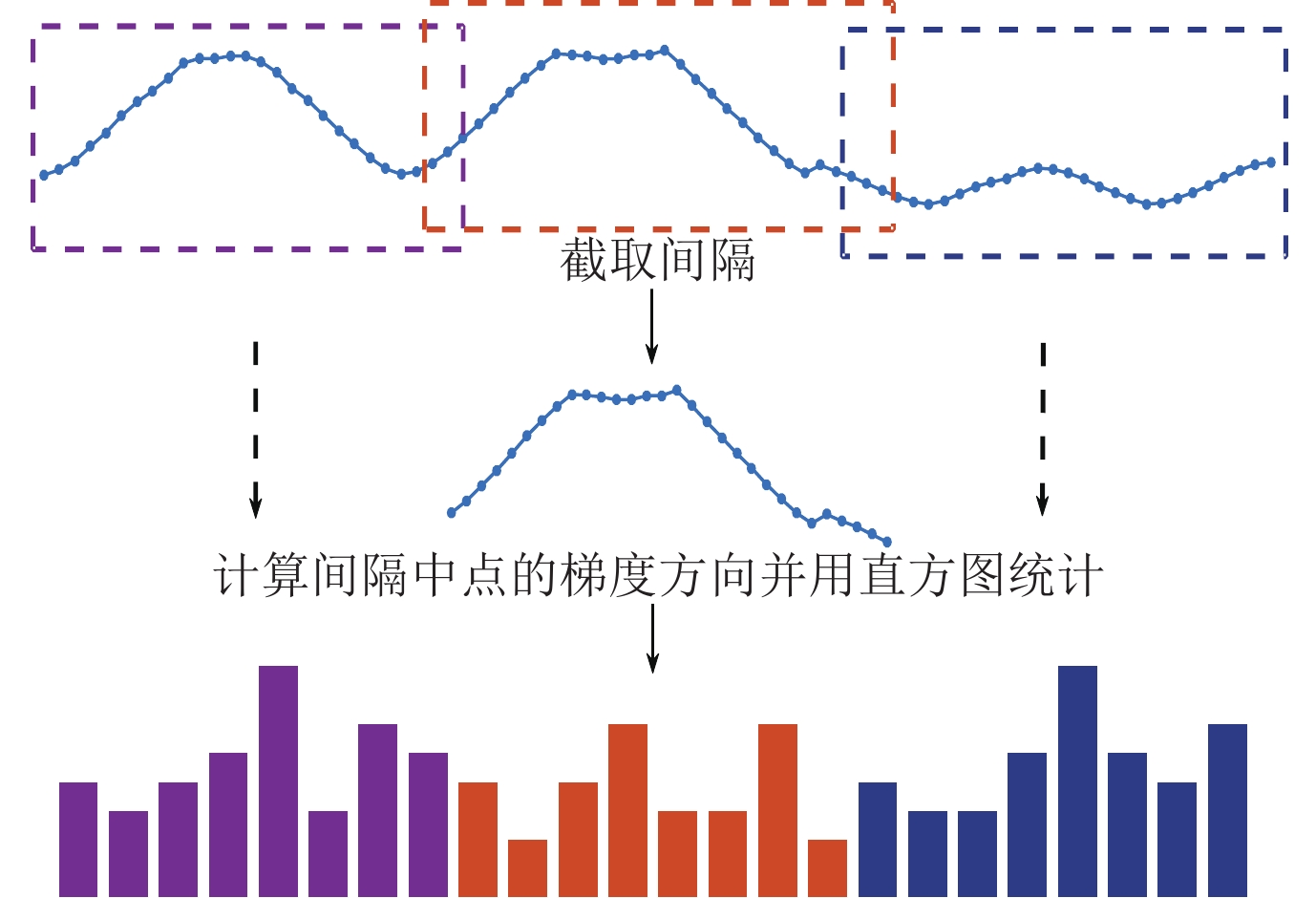
为了解决时间序列相似性度量过程中局部信息匹配不充分的问题, 一些研究者试图先将序列的局部形状作为特征提取出来, 然后再进行相似性度量. 例如, Deng和Baydogan等人[16, 17]提出用直线线性拟合子序列的斜率; Zhao等人[11, 30]将原本用于计算机视觉领域的HOG扩展到了时间序列数据, 提出用HOG-1D局部特征描述子来表示序列中点的局部结构信息. HOG-1D继承了HOG的核心思想, 即通过将时间序列点局部结构进行直方图表示来反映序列的局部结构信息. 时间序列中点的HOG-1D局部特征描述子的具体生成过程如图2所示, 首先是从原序列中提取该点的对应子序列S(如图2中蓝色线所示), 然后将其分为若干间隔I={I1, I2, …, Ih}(图2中矩形虚线框圈起部分). 对于每一个间隔Ii, 统计Ii中所有点的梯度和方向, 可以得到一个方向梯度直方图. 最后串联h个间隔的直方图来构成子序列S的特征描述子, 即HOG-1D局部特征描述子(对于HOG-1D更为详细的信息可参考文献[30]). 方向梯度直方图的统计特性使得HOG-1D对观测噪声的敏感性进一步降低, 同时直方图的串联又能很好的捕捉时间信息.
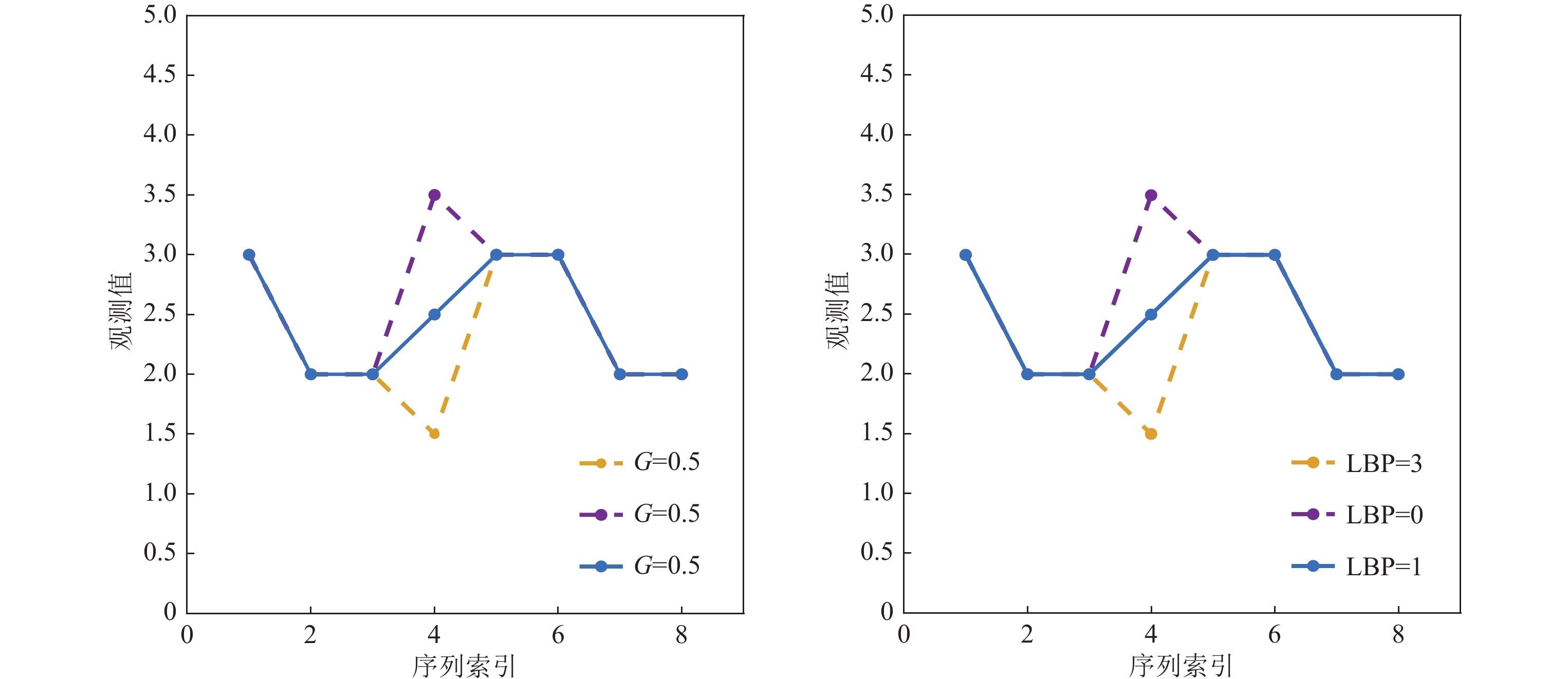
类似于HOG-1D的局部特征提取方式是通过考虑点的梯度或斜率等来编码时间序列局部结构信息的, 之后再用这些描述子形成的新特征空间进行相似性度量. 这种特征提取方式在一定程度上缓解了时间序列的局部结构信息丢失问题. 然而, 受梯度或斜率等计算方式的限制, 这种类型的子序列编码方式是有缺陷的. 如图3(左)所示为一条子序列, 在x=4位置, 3种形状结构下点的梯度G都为0.5, 点的局部差异并没有充分体现出来. 然而本文算法使用点的局部二进制值的离散特性有效的区分了点的局部差异(如图3(右)所示). 可以看到, 在x=4处3种形状结构下的点的二进制值编码是明显不同的(LBP值分别为3、0、1), 点的局部细节信息得到了更为精准的描述.
2 基于局部二进制模式的局部特征表示针对传统局部特征描述子对时间序列点的局部结构信息描述不充分的问题, 本文提出了一种基于局部二进制模式的时间序列的局部特征描述子LBPT. 本节将详细介绍该描述子的生成过程.
|
Fig. 2 Generation process of HOG-1D local feature descriptor 图 2 HOG-1D局部特征描述子生成过程 |
|
Fig. 3 Comparison of local information coding effect of time series points 图 3 时间序列点的局部信息编码效果比较 |
2.1 滤波技术
图像处理问题中, 为了缓解各种噪声产生的影响, 会用到各种滤波技术, 比如常见的有均值滤波, 中值滤波和高斯滤波等. 类似的, 时间序列数据也存在噪声. 因此, 为了缓解数据噪声对分类产生的影响, 借鉴图像处理中的经验, 本文中将首先使用滤波技术对时间序列数据进行降噪处理. 由于均值滤波为线性滤波, 其主要采用邻域平均的思想, 相比于其他滤波技术, 该方法较为简单、速度较快. 鉴于此, 本文将采用均值滤波对序列进行处理, 即通过设置滑动窗口w的大小来确定每一个序列点的局部近邻子序列的长度, 然后用局部近邻子序列的均值代替原始序列点. 给定时间序列T={t1, t2,…, tm}, 则其每一个点ti的滤波过程如公式(1):
| tfi=1w∑i+(w−1)/2j=i−w/2tj w/2<i⩽m−(w−1)/2tfi=1w(∑i+(w−1)/2j=1tj + ∑w/2−i+1j=1t1 ) 1⩽i⩽w/2tfi=1w(∑mj=i−w/2tj+∑(w−1)/2+i−mj=1tm) m−(w−1)/2<i⩽m | (1) |
其中, w代表滑动窗口大小, tfi表示ti滤波之后的序列点值, tj表示在滑动窗口大小为w时时间序列T中点ti的近邻点, t1和tm则表示时间序列T的前后两个端点.
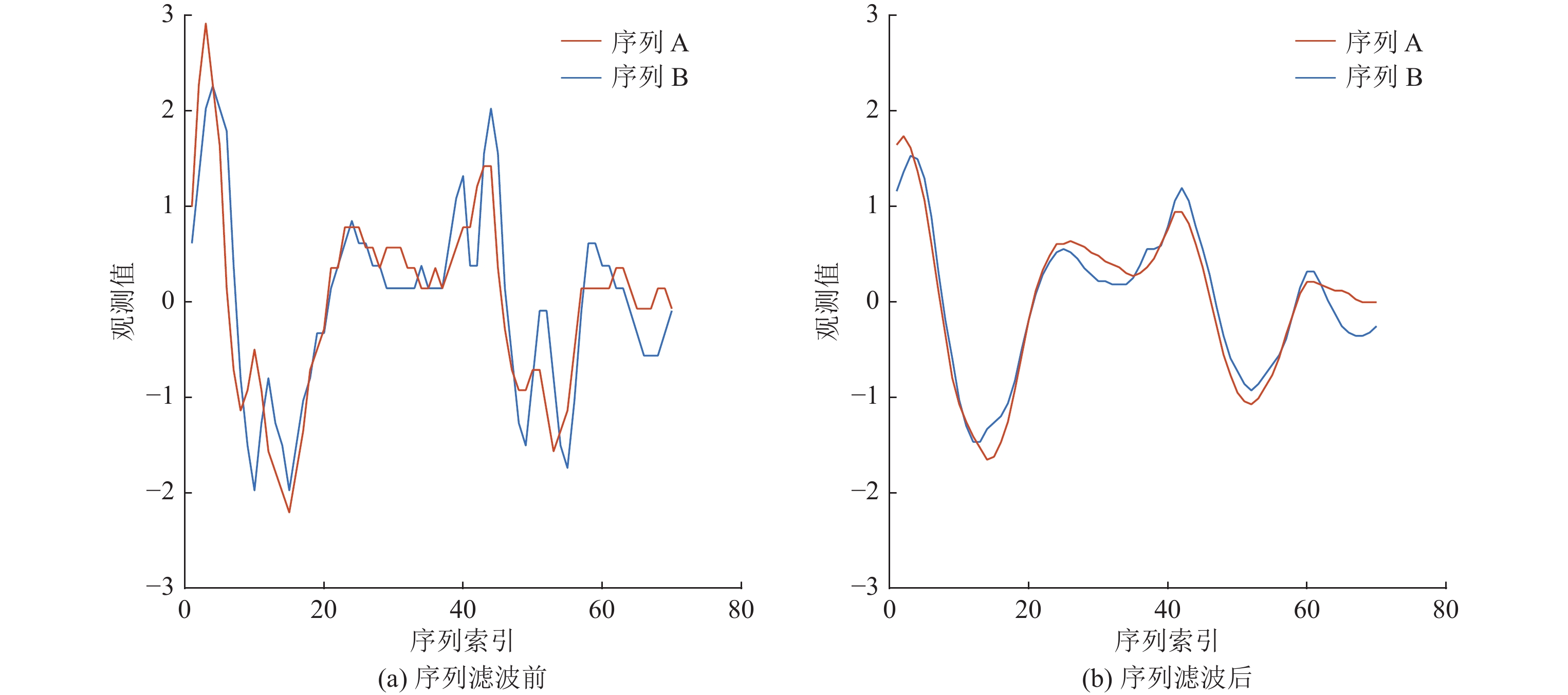
通过公式(1)可以得到滤波之后的序列Tf={tf1, tf2,…, tfm}. 经过滤波处理之后的序列, 因为噪声引起的局部波动会得到明显的缓解. 图(4)是SonyAIBORobotSurface1数据集中类标相同的两条时间序列滤波前后的对比图, 可以看出, 跟不进行滤波(图4(左))相比, 经过滤波之后的两条序列(图4(右))更趋于重合, 因此也更有可能被匹配到同一类中去.
|
Fig. 4 Comparison of two time series with the same class labels in SonyAIBORobotSurface1 dataset before and after filtering 图 4 SonyAIBORobotSurface1数据集中类标签相同的两条时间序列滤波前后比较 |
2.2 基于局部二进制模式的时间序列局部特征描述子
局部二进制模式LBP最初是由Ojala等人[13]提出的一种用于纹理分类的特征描述子, 目前已被广泛应用到了图像分析[31]、人脸识别[32, 33]、目标识别[34]等多个领域. 该描述子只需通过简单的二进制运算就可以获得, 具有较低的计算复杂度, 更重要的是该描述子本身的离散特性使其具有较高的特征鉴别能力(如图3所示).
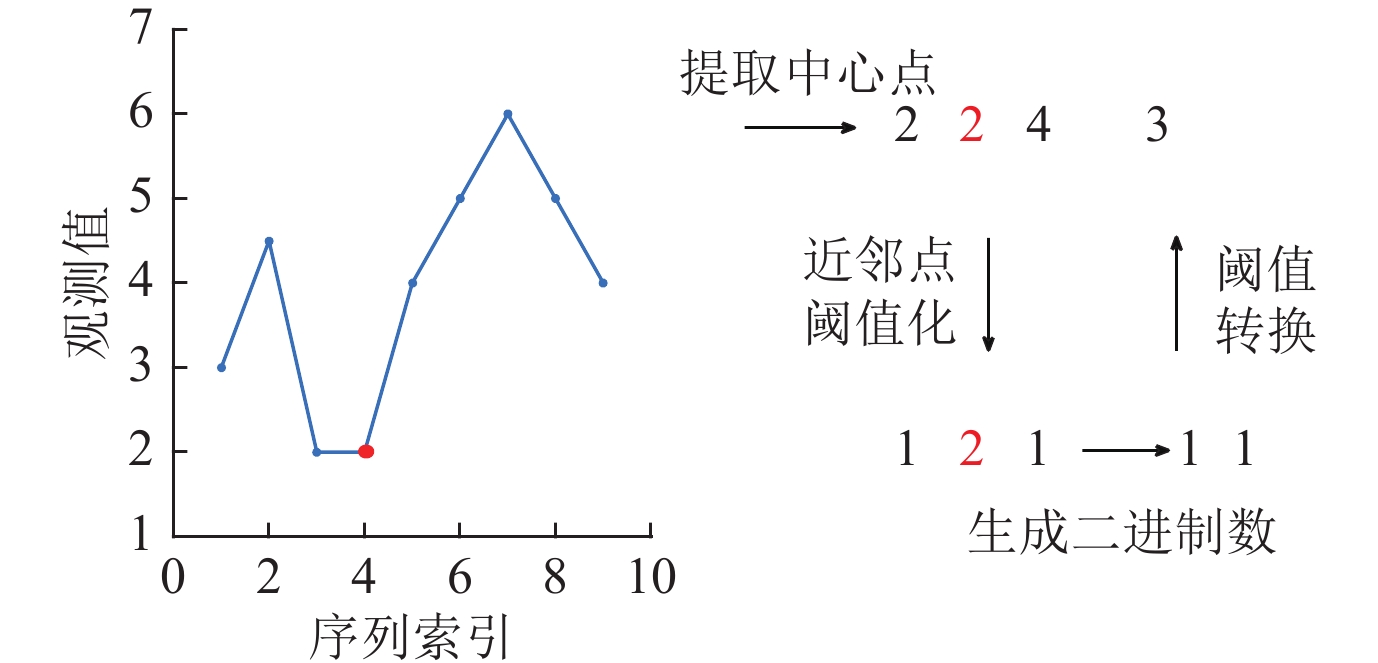
鉴于LBP对局部特征较高的鉴别能力及其低复杂性, 本文提出了一种新的应用于一维时间序列的局部特征描述子LBPT. LBPT描述子本质上是通过将时间序列点对应子序列上的每个点作为中心点, 再将其周围近邻点进行二进制阈值化处理, 然后把得到的多位二进制数转换为LBP整数值, 最后对子序列中所有点的LBP值进行直方图统计. 图5是一条子序列中任一点的LBP值生成过程. 需要注意的是, 子序列中点的近邻点的数量是可以调整的, 但不宜过多, 否则会导致最终生成的描述子维度过高. 简单起见, 图5中我们选取的是两个近邻点.
|
Fig. 5 LBP value generation process of time series points 图 5 时间序列点的LBP值生成过程 |
这里给出本文的LBPT特征描述子的详细生成过程, 如图6所示. 给定一条子序列S={s1, s2,…, sl}, 计算每个点si的二进制模式值LBPi, 其计算方式如公式(2)和公式(3)所示.
| LBPi=N−1∑j=0b(si+N−j−si)2j+2N∑j=N+1b(si+N−j−si)2j−1 | (2) |
| b(Δs)=(1,Δs⩾00,Δs<0) | (3) |
其中, Δs表示的是si近邻点与si的差值, N表示计算点si所使用的近邻点对数. 需要注意的是, 此时的LBPT描述子长度为4N, 增长较快. 因此, 简单起见, 本文中只考虑N=1的情况. 当求出子序列中所有点的LBP值之后, 用直方图统计不同LBP模式值的点数量. 最终用直方图统计结果来表示原始时间序列点的局部结构信息, 即LBPT特征描述子(如图6中最后生成的特征描述子为{1, 3, 3, 4}).

|
Fig. 6 LBPT local feature descriptor generation process 图 6 LBPT局部特征描述子生成过程 |
算法1给出了本文的LBPT局部特征描述子的生成过程. 其中第1行是数据的初始化操作; 第2–4行是计算所有子序列点的LBP值; 最后第5–10行是对LBP值进行累加得到最终的LBPT局部特征描述子. 需要注意的是, 虽然该特征描述子生成过程的时间复杂度为O(2N·seqlen), 但这里N通常只需取相对较小的值即可, 例如N=1, 因此其时间复杂度在实际情况下可以近似为O(seqlen).
算法1. LBPT局部特征描述子生成过程.
输入. 子序列S, 近邻点对数N;
输出. LBPT局部特征描述子.
1. 初始化:子序列长度seqlen, 描述符数组DS[4N], LBP值存储数组lbp[seqlen].
2. for(j=1;j<=seqlen;++)
3. 用公式(2)(3)计算每一个子序列点的LBP值lbp[j].
4. end for
5. for(j=1;j<=seqlen;j++)
6. for(k=0;k<4N;k++)
7. if(k==lbp[j])
8. DS[k]←DS[k]+1
9. end for
10. end for
11. return DS
3 基于局部特征加权的相似性度量算法本节首先简单介绍传统动态时间规整算法, 然后对本文所提出的基于局部特征加权的相似性度量算法进行了详细介绍.
3.1 动态时间规整DTW是一种动态规划算法, 能够通过非线性扭曲找到时间序列间的最优匹配路径并进行序列间的相似性度量. 同时, DTW适用于单变量和多变量的时间序列. 简单起见, 本文中只考虑等长单变量时间序列.
给定两条时间序列P={p1, p2,…, pn}和Q={q1, q2,…, qn}. 定义P, Q之间的点对距离矩阵D∈Rn×n, 其中每个元素d(pi, qj), 1≤i, j≤n, 表示pi, qj之间的距离. 对于距离的度量通常使用欧几里得距离, 即d(pi, qj)=|pi−qj|. 对齐P, Q的目的是找到一条规整路径W=((e1, f1), (e2, f2),…, (el, fl)), n≤l≤(2n−1), 该路径将序列P中索引为ei的点与序列Q中索引为fi的点进行匹配. 最后求得的路径W满足
| {(e1,f1)=(1,1)(el,fl)=(n,n)(ei+1,fi+1)−(ei,fi)∈{(1,0),(1,1),(0,1)} | (4) |
这里用γ(i, j)表示序列P, Q间的累积距离, 其递归过程如公式(5)和公式(6):
| γ(i,j)=d(pi,qj)+min | (5) |
| DTW(P, Q) = \gamma (n, n) | (6) |
在一定的约束条件下, DTW的确能够获得全局的最优对齐, 但它忽略了序列的局部结构信息. HOG-1D这种基于梯度或斜率的局部特征描述子虽然着眼于局部信息, 但也存在对原始子序列编码不够精确的问题(如图3所示). 鉴于此, 本文考虑利用LBP较高的局部特征鉴别能力来缓解传统的基于梯度或斜率的局部特征描述子对序列的局部结构信息表示不充分的问题, 提出了基于HOG-1D和LBPT加权的相似性度量算法. 给定两条时间序列P={p1, p2,…, pn}, P∈Rn. 和Q={q1, q2,…, qn}, Q∈Rn. 用PG={
| d({p_i}, {q_j}) = \sqrt {\delta {d_{HOG - 1D}}\left( {{p_i}, {q_j}} \right) + (1 - \delta ){d_{LBPT}}\left( {{p_i}, {q_j}} \right)} | (7) |
| \gamma \left( {\left. {i, j} \right)} \right. = d({p_i}, {q_j}) + \min{\text{\{ }}\gamma (i - 1, j - 1), \gamma (i - 1, j), \gamma (i, j - 1){\text{\} }} | (8) |
| LGBDTW(P, Q) = \gamma (n, n) | (9) |
其中, dHOG-1D(pi, qj)和dLBPT(pi, qj)分别表示时间序列点i、j的HOG-1D特征描述子之间距离和LBPT特征描述子之间的距离, 其计算方式如公式(10)和公式(11):
| {d_{HOG - 1D}}({p_i}, {q_j}) = {\sum\nolimits_{a = 1}^h {|p_{ia}^G - q_{ja}^G|} ^2} | (10) |
| {d_{LBPT}}({p_i}, {q_j}) = {\sum\nolimits_{a = 1}^{{4^N}} {|p_{ia}^B - q_{ja}^B|} ^2} | (11) |
其中, h表示的是HOG-1D局部特征描述子的长度, 其大小随着时间序列点所对应的子序列被划分的间隔数发生变化. 在公式(7)中, 0≤δ≤1是一个平衡因子, 它反映的是在距离度量过程中HOG-1D和LBPT两种描述子所占比重; N表示的是在计算子序列中点的LBP值时使用的近邻点对数. 由此得到基于HOG-1D和LBPT两种特征描述子的加权动态时间规整算法LGBDTW.
算法2给出了本文的相似性度量算法的伪代码. 其中第1行是相关数据的初始化; 第2-4行是对原始时间序列进行滤波; 第5到10行是基于HOG-1D及LBPT两种特征描述子的相似性度量. 需要注意的是, DTW算法的时间复杂度为O(n2), 而对于本文算法, 考虑到N、k等的实际设置值都要远小于n, 所以计算HOG-1D及LBPT描述子时的复杂度可以近似表示为O(n), 同时LGBDTW相似性度量算法复杂度为O(n2), 所以本文算法最终复杂度可以近似表示为O(n2), 接近于DTW.
算法2. LGBDTW相似性度量算法.
输入: P、Q, 滤波器窗口大小w, 子序列长度k, HOG-1D描述子长度h, 平衡因子δ, 近邻点对数N;
输出: LGBDTW(P, Q).
1. 初始化: 描述符序列PG, QG, PB, QB以及序列P, Q长度qlen.
2. for(j=1;j<=qlen;j++)
3. 用公式(1)对P, Q中的点进行滤波.
4. end for
5. for(j=1;j<=qlen;j++)
6. 以长度k提取P, Q的第j个点的子序列Pj, Qj.
7. 用算法1计算LBPT描述子PB[j], QB[j].
8. 同时生成传统的HOG-1D描述子PG[j], QG[j].
9. end for
10. 用公式(7)–公式(11)计算P, Q的距离LGBDTW(P, Q)
11. return LGBDTW(P, Q)
4 实验分析本节对所提出算法的相关实验内容进行介绍, 实验中所使用的73个数据集均来源于UCR时间序列数据库[35]. 这里首先介绍一些参数对实验的影响, 然后将本文提出的算法的分类效果与当前比较流行的分类器进行了比较.
4.1 参数分析及选取正如前面算法中所述, 本文算法受到一些参数的影响. 简单起见, 参考文献[11]中的设置, 实验中将时间序列点的对应子序列长度k固定为30; HOG-1D长度h固定为16; 此外, 因为LBPT描述子的长度随近邻点对数N的变化增长较快, 为方便测试, 我们将N固定为1, 即每一个时间序列点的LBPT描述子为一个4维向量. 在保持这些参数不变的前提下, 本文分别测试了滤波器窗口w以及平衡因子δ对分类结果的影响. 当测试滤波器窗口参数w时, 将δ固定为0.5; 当测试平衡因子δ时, 将w大小固定为7.
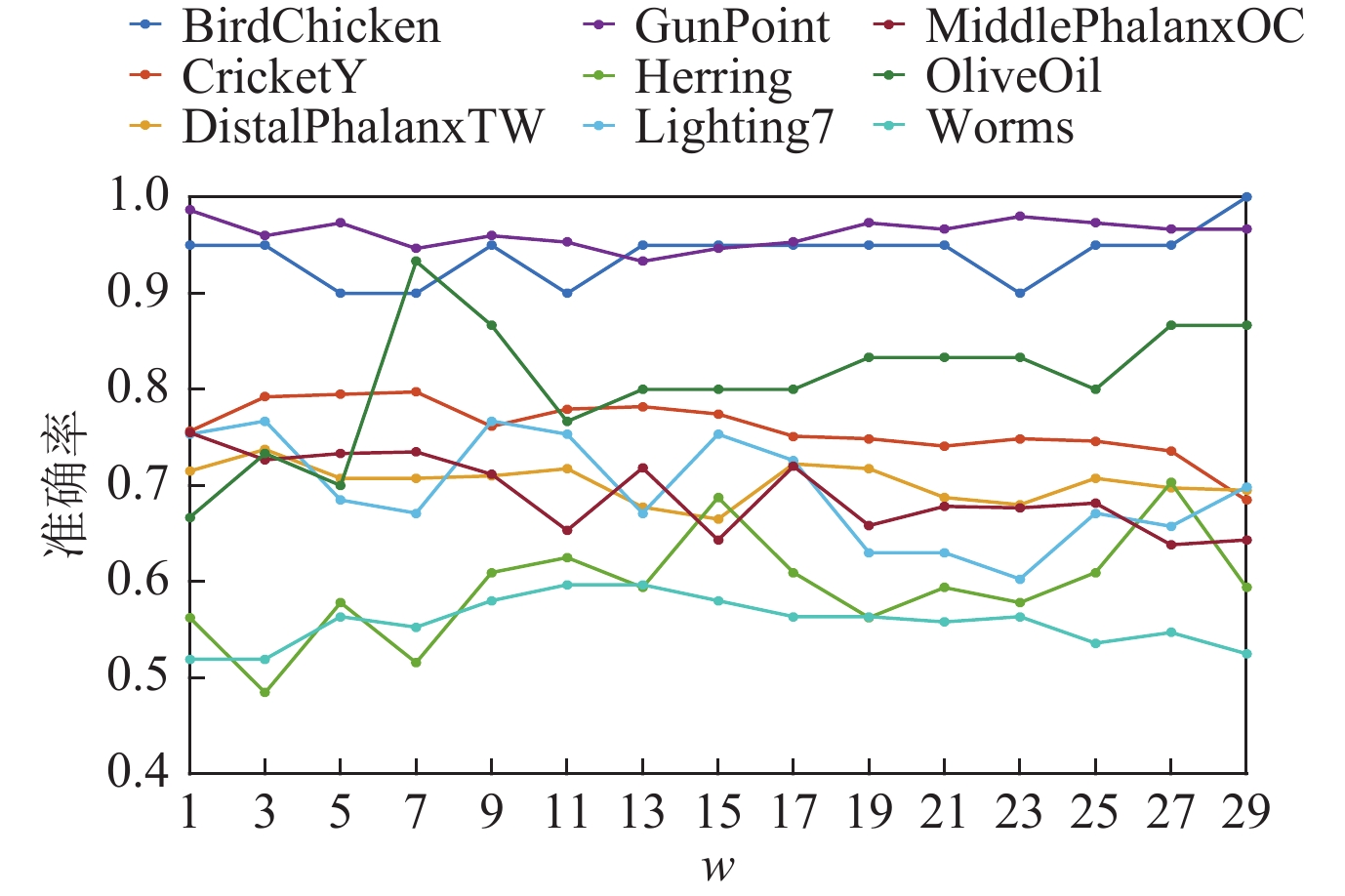
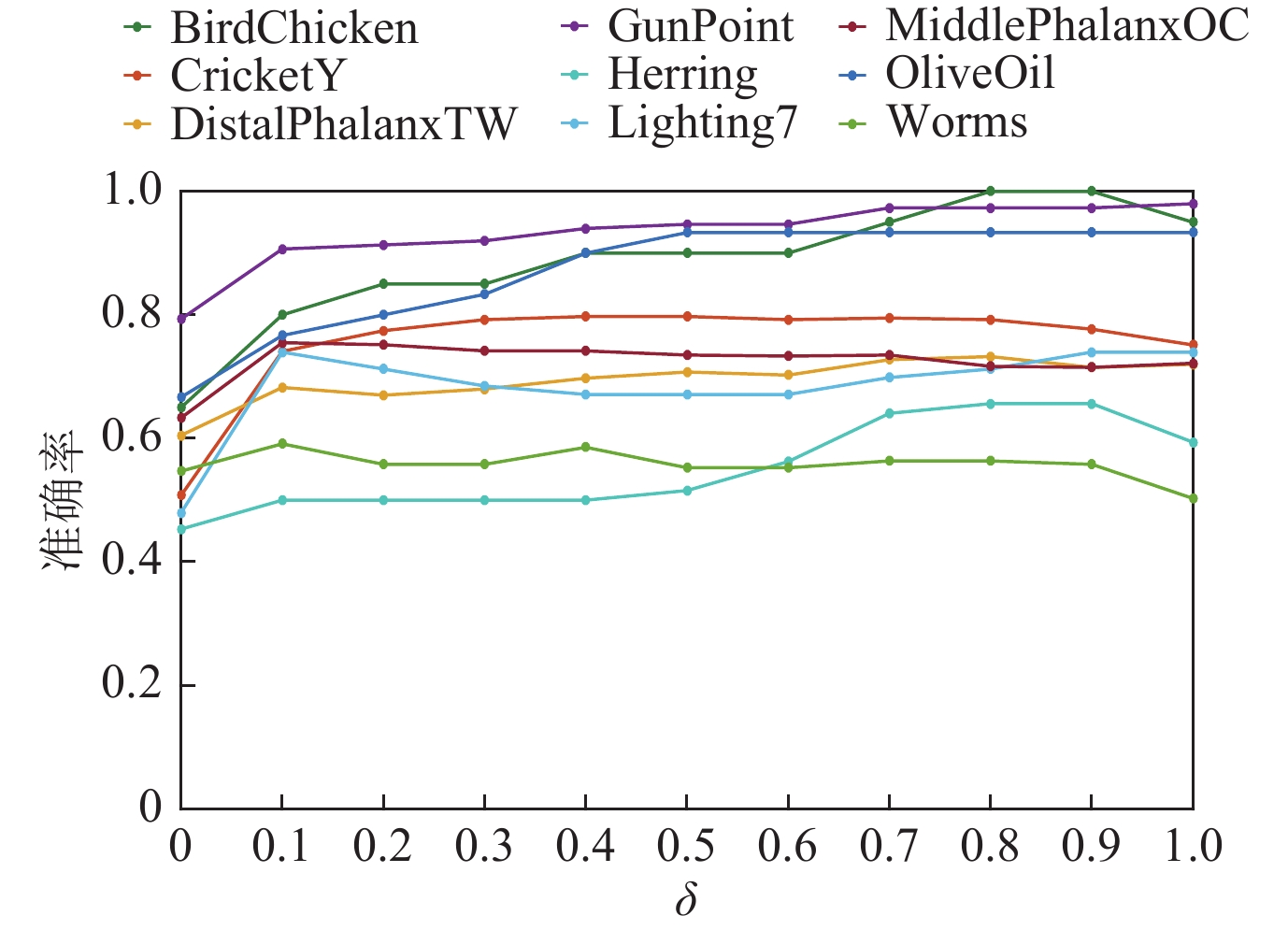
首先我们在9个时间序列数据集上测试了滤波器窗口大小w在[1, 29]范围内变化时对分类准确率的影响, 测试结果如图7所示. 图7展示了随着w大小的变化LGBDTW分类准确率的变化趋势. 从图中可以看出, 在所测试的数据集中, 随着w的增加, 大多数数据集的准确率都有一个增减过程. 需要注意的是当w=1时, 实质上是没有对原始时间序列进行滤波. 当w处于11到23之间时, 分类准确率相对较高且稳定, 而在w超过23之后, 部分数据集的准确率开始明显下降, 因此, 考虑到计算复杂性及准确率, 本文算法取w=15. 而对于平衡因子δ, 如图8所示, 在所测试的9个数据集上, 随着平衡因子δ的变化, 大多数数据集的准确率在δ∈[0, 1]之间有一个增减过程. 其中当δ=0时, 表示的是单独使用LBPT描述子时的分类准确率;当δ=1时, 表示的是单独使用HOG-1D描述子时的分类准确率. 可以观察到, 在δ处于0.6到0.9之间时, 分类准确率相对稳定并达到最高. 因此, 简单起见, 我们在分类过程中将平衡因子δ固定为0.8, 以达到较为理想的分类效果.
|
Fig. 7 The trend of classification accuracy with filter window size w 图 7 分类准确率随滤波器窗口大小w的变化趋势 |
|
Fig. 8 The trend of classification accuracy with equilibrium factor δ 图 8 分类准确率随平衡因子δ的变化趋势 |
4.2 分类器性能分析
在本节中, 我们将本文算法LGBDTW与1NN结合在73个UCR数据集上进行了分类测试, 并将分类效果与现在比较流行的分类器进行了比较. 这些算法的结果均采用的是UCR时间序列数据库或者是原论文中作者提供的结果.
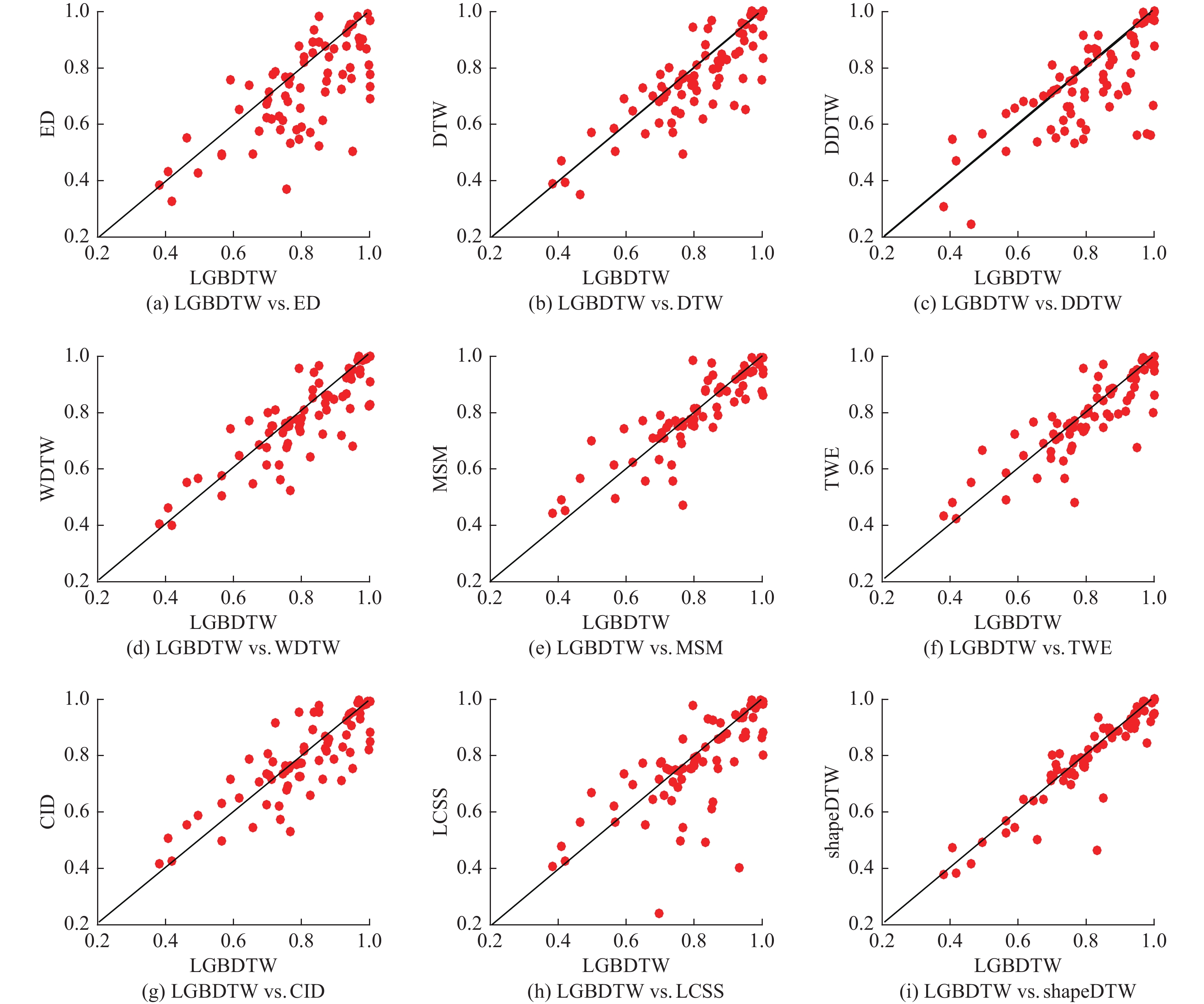
4.2.1 与基于距离的分类器进行比较本节将LGBDTW与其他几个当前比较流行的基于距离的分类方法进行了比较. 例如, 比较典型的有欧氏距离(ED)、最长公共子序列(LCSS)、DTW、DDTW、WDTW、复杂性-不变DTW (CID)、MSM、TWE以及shapeDTW. 表1展示的是以上分类器以及LGBDTW在73个数据集上的准确率对比(由于篇幅原因, 这里只展示DTW及其衍生类型算法的准确率). 其中加粗表示6个分类器中在该数据集上表现最优的分类器, 从表1可以看出, DTW、DDTW、WDTW、CID、shapeDTW、LGBDTW分别在8、10、9、18、16和25个数据集上表现最好. 在平均准确率方面, LGBDTW为80.2%, 也优于其他的分类器. 为了更加形象的展示所提算法与其他分类算法的分类效果, 本文绘制了LGBDTW与其他9个算法在73个数据集上的分类准确率对比图(如图9, 其中x, y坐标轴数值代表的是分类准确率). 图中的每个红色点表示一个数据集, 点落在斜线下方表示该数据集上LGBDTW的分类效果更好.
| Table 1 Comparison of classification accuracy between LGBDTW and other classifiers 表 1 LGBDTW与其他分类器分类准确率比较结果 |
从图9可以看到, 在分类准确率方面, LGBDTW在大多数数据集上优于其他的基于距离的分类方法. 在被测试的73个数据集中, 同DTW比较, LGBDTW在49个(2个等于)数据集上优于DTW, 其中有5个数据集的准确率提升超过20%. 此外, 同DDTW、WDTW、CID、以及shapeDTW这些DTW的衍生算法相比, LGBDTW分别在49 (1个等于)、42 (3个等于)、43 (1个等于)、47 (2个等于)个数据集上表现更好. 而对于ED、LCSS、MSM以及TWE这几个方法的分类结果, LGBDTW也分别在48、47、36 (1个等于)、42 (2个等于)个数据集上优于它们. 需要注意的是, 在LGBDTW与MSM的比较中, 虽然MSM在准确率占优的数据集数量上比LGBDTW多2个, 但如表1所示, LGBDTW的最优准确率数量以及平均准确率都要高于MSM.
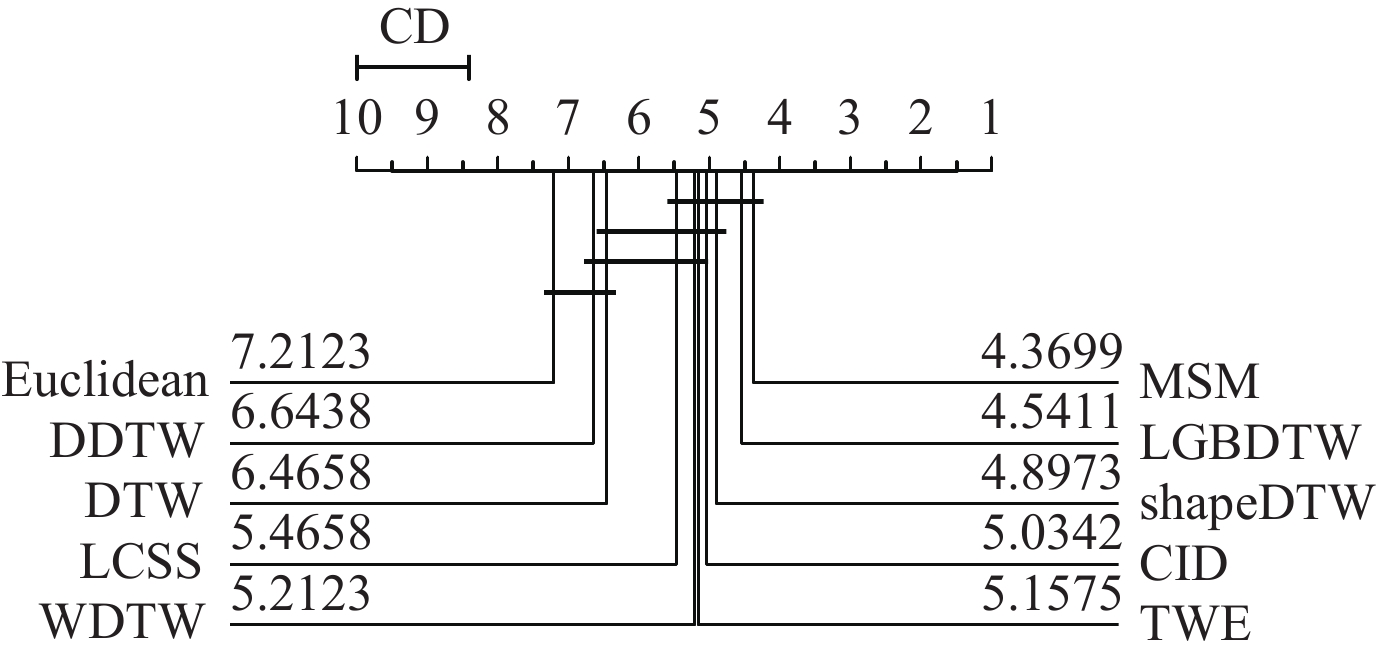
为了更全面评价这10个分类器在多个数据集上的分类效果, 本文还采用了Demšar所提出的临界差异图[36](如图10)来对多个分类器进行评分, 其中评分越小表示分类效果越好. 从图10可以看出, LGBDTW所表现出来的分类效果跟MSM没有显著性差异, 基本都是属于最好的.
|
Fig. 10 The score result of the distance based classifiers 图 10 基于距离的分类器评分结果 |
此外, 为了进一步分析不同数据特性(即数据集类型)对本文算法LGBDTW分类效果所产生的影响, 我们利用表1分别对不同数据集类型下的LGBDTW分类准确率进行了比较分析. 本文实验中所涉及到的数据集主要包括8种类型, 即device、audio、ecg、image、motion、sensor、simulated以及spectro. 对表1的分析结果表明, LGBDTW在DEVICE、AUDIO等类型数据集下的分类准确率大多数情况下相对其他类型数据比较低. 具体地, DEVICE类型数据集的准确率大多低于0.7, 例如RefrigerationDevices为0.496, Computers为0.676. 相反的, LGBDTW在simulated以及ECG等类型数据集上的准确率多数超过了0.9, 例如ECG类型下的ECGFiveDays为0.998, TwoLeadECG为0.970.
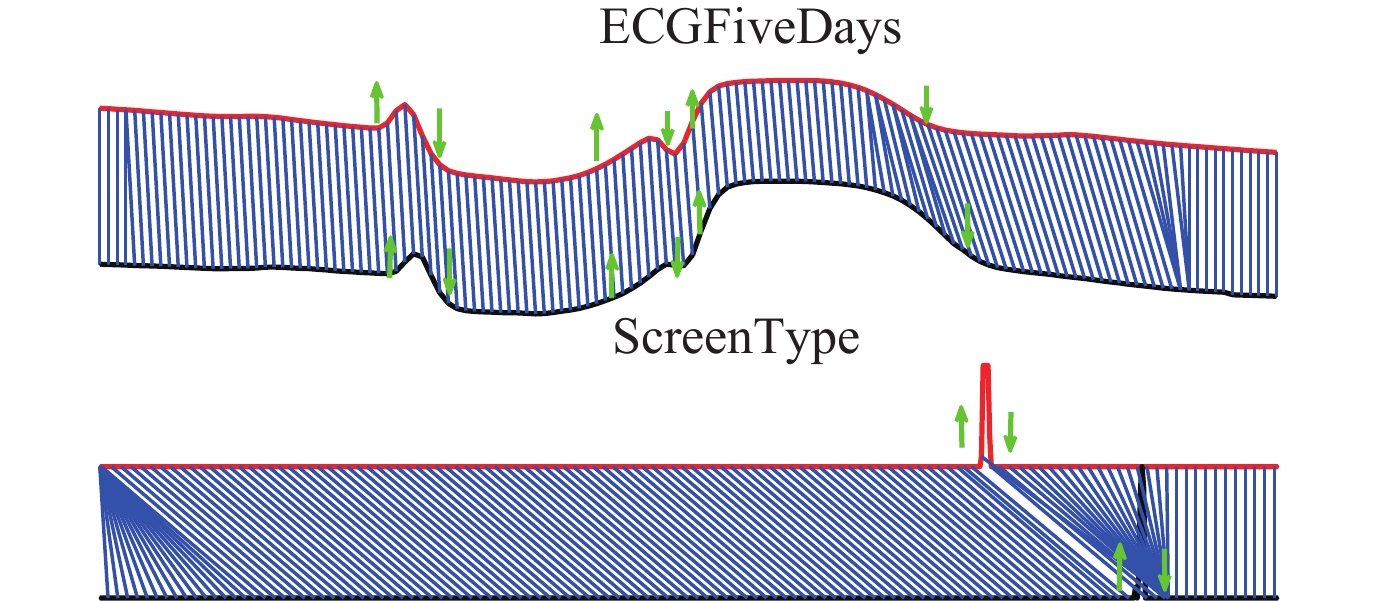
为了分析造成以上差异的原因, 我们分别选取device以及ECG类型数据集中的数据对序列结构进行了比较. DEVICE类型数据集主要反映的是不同家用电器一天时间内的用电记录而多数家用电器在一天时间内的用电状态改变次数是非常有限的, 其用电数据序列大多数时间是处于稳定的状态; ECG类型数据集主要反映的是人体的心率活动的心电图, 具有明显的局部波动情况. 图11展示的是DEVICE类型数据集中的ScreenType数据序列(序列类型包括3类, 分别表示3种家用电器的用电记录)与ECG类型数据集中的ECGFiveDays数据序列(序列类型包括2类, 表示同一个人不同两天中的心电图记录)的对齐结果比较, 其中绿色箭头表示序列的局部上下波动. 图的上半部分表示的是ECGFiveDays数据集中两条同类序列的对齐, 下半部分表示的是ScreenType数据集中两条同类序列的对齐. 从图中可以看出, ECGFiveDays数据序列包含有相当数量的波动, 即含有丰富的局部特征. 而ScreenType数据序列则含有极少量的波动, 即含有极少的局部特征. 同时可以看出ECGFiveDays序列的对齐结果明显优于ScreenType, 其中ScreenType的对齐出现了较为严重的局部错误对齐, 这在分类过程中很容易导致序列距离度量出现偏差, 最终造成错误分类. 由此可知, 当待分类序列中包含的局部特征信息不足时, LGBDTW算法的局部辨别能力很有可能会被削弱. 相反的, 当待分类序列中包含丰富的局部特征信息时, LGBDTW能够发挥出更好的分类性能.
|
Fig. 11 Comparison of local features between ECGFiveDays and ScreenType datasets 图 11 ECGFiveDays与ScreenType数据集序列局部特征对比 |
4.2.2 与基于特征的分类器进行比较
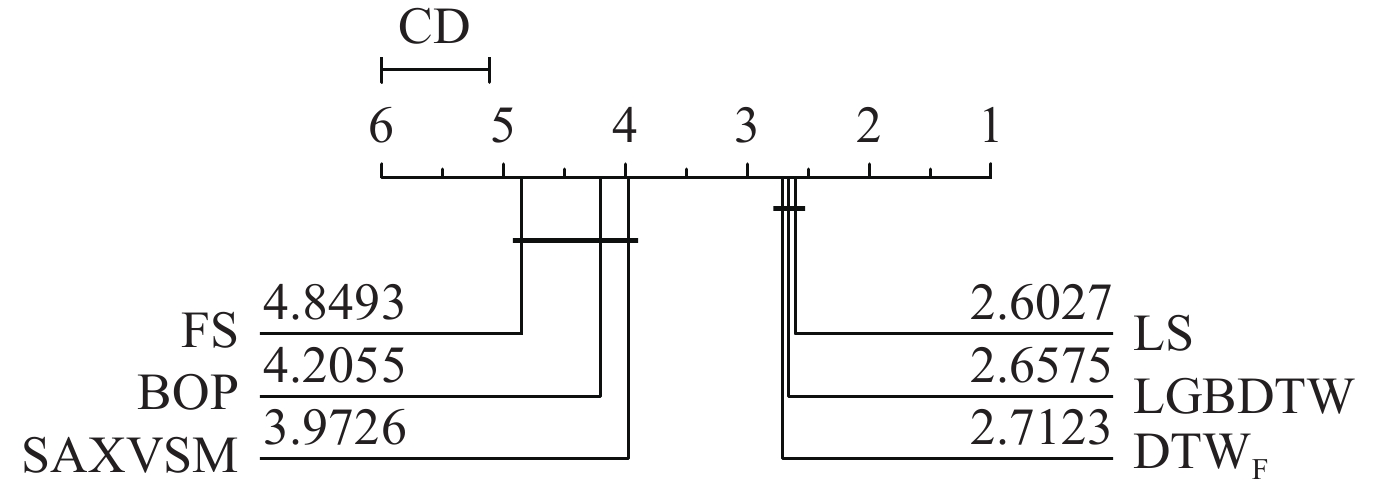
在本节中, 将对本文LGBDTW算法与目前流行的基于特征的时间序列分类器进行比较, 例如, 快速shapelet (FS)[37], 学习shapelet (LS)[38], DTW特征(DTWF)[39], 模式包(BOP)[40], 符号聚合近似向量空间模型(SAXVSM)[41]等. 这里我们同样根据分类准确率对这些分类器进行了评分(如图12), 从图中可以看到, LGBDTW的评分结果基本上与DTWF和LS相同, 并且明显优于FS、BOP和SAXVSM这3个分类器.
|
Fig. 12 The score result of the feature based classifiers 图 12 基于特征的分类器评分结果 |
4.2.3 与基于深度学习的分类器进行比较
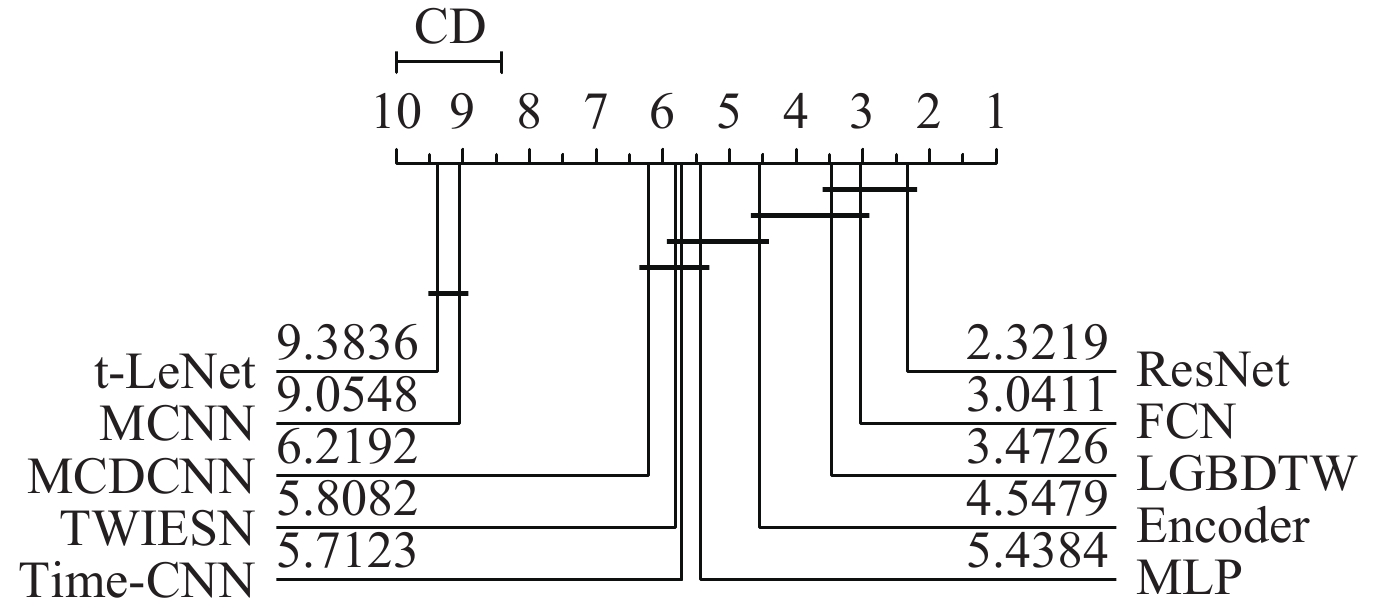
近些年深度学习也开始被广泛应用到时间序列分类问题中来. 本节中, 我们将本文LGBDTW算法与现有的比较流行的基于深度学习的分类器进行比较, 例如, MLP、FCN、ResNet[23]、Encoder[42]、MCNN[22]、t-LeNet[23]、MCDCNN[43]、Time-CNN[24]以及TWIESN[44]等, 比较结果如图13所示. 从图13可以看到, LGBDTW与ResNet和FCN模型的评分结果相近, 这表明它们的分类效果并没有显著性差异. 而这些分类器是目前基于深度学习的时间序列分类模型中分类效果最好的, 也就说明LGBDTW优于大多数的基于深度学习的时间序列分类模型, 从图13中其他分类模型的评分也可以看出这一点. 更重要的是, 深度学习模型往往伴随大量的参数调整, 在时间消耗方面明显高于LGBDTW. 此外, LGBDTW在可解释性方面跟这些基于深度学习的分类器相比是占有绝对优势的, 因为大多数此类模型可解释性较弱甚至通常不具有可解释性.
|
Fig. 9 Comparison of classification accuracy between LGBDTW and other distance based classifiers 图 9 LGBDTW与其他基于距离的分类器的分类正确率比较结果 |
|
Fig. 13 The score results of deep learning based classifiers 图 13 基于深度学习的分类器评分结果 |
4.2.4 与基于集成的分类器进行比较
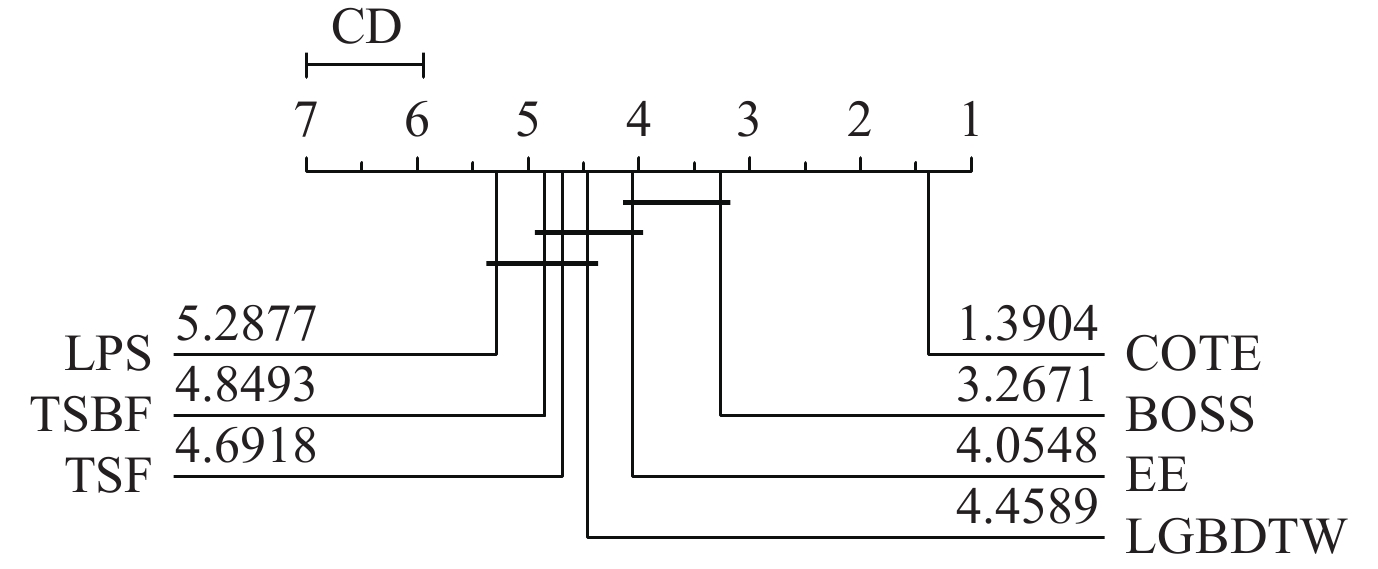
在本节中, 我们将本文的LGBDTW算法与当前比较流行的集成分类器进行比较. 集成分类器是通过集成一系列性能较弱的分类器, 以达到更好的分类性能. 在时间序列领域, 比较常见的集成分类器有很多, 例如, 时间序列森林(TSF)[16], 时间序列特征包(TSBF)[17], 学习模式相似性(LPS)[18], 动态集成(EE)以及COTE[38]等. 这里同样以临界差异图的方式将它们与LGBDTW进行了比较, 结果如图14所示. 从图中可以看出, LGBDTW与EE的分类效果没有显著性差异, 但优于TSF、TSBF和LPS. 此外, 虽然LGBDTW比COTE和EE以及BOSS稍微弱一些, 但就运行速度上来讲, 它比BOSS, EE或者COTE这种集成几种甚至几百种不同算法的分类器要快得多. 同时, LGBDTW还可以集成到这些算法中来进一步提高它们的分类准确率.
|
Fig. 14 The score results of ensemble classifiers 图 14 基于集成的分类器评分结果 |
4.3 运行时间
通过前面对分类准确率的比较可以看出LGBDTW优于大多数分类器. 虽然结果上比个别分类器要弱一些, 但这并不意味着LGBDTW就整体弱于这些分类器. 因此, 我们分别对LGBDTW以及几个在临界差异图中跟其评分差异较大的分类器进行了运行时间测试, 这些分类器包括集成分类器BOSS, EE和COTE. 对于基于深度学习的分类器, 由于涉及大量的参数调整, 这里将不再进行测试. 我们分别在18个相对较小的数据集上对分类器的运行时间进行了测试, 测试结果如图15所示, 我们对它们在每个数据集上的十次运行时间均值进行了比较. 从图中可以看出, 与EE和COTE相比, LGBDTW在运行时间上至少占有一个数量级的优势, 而对于BOSS分类器, LGBDTW也在多数数据集上的运行时间少于它.
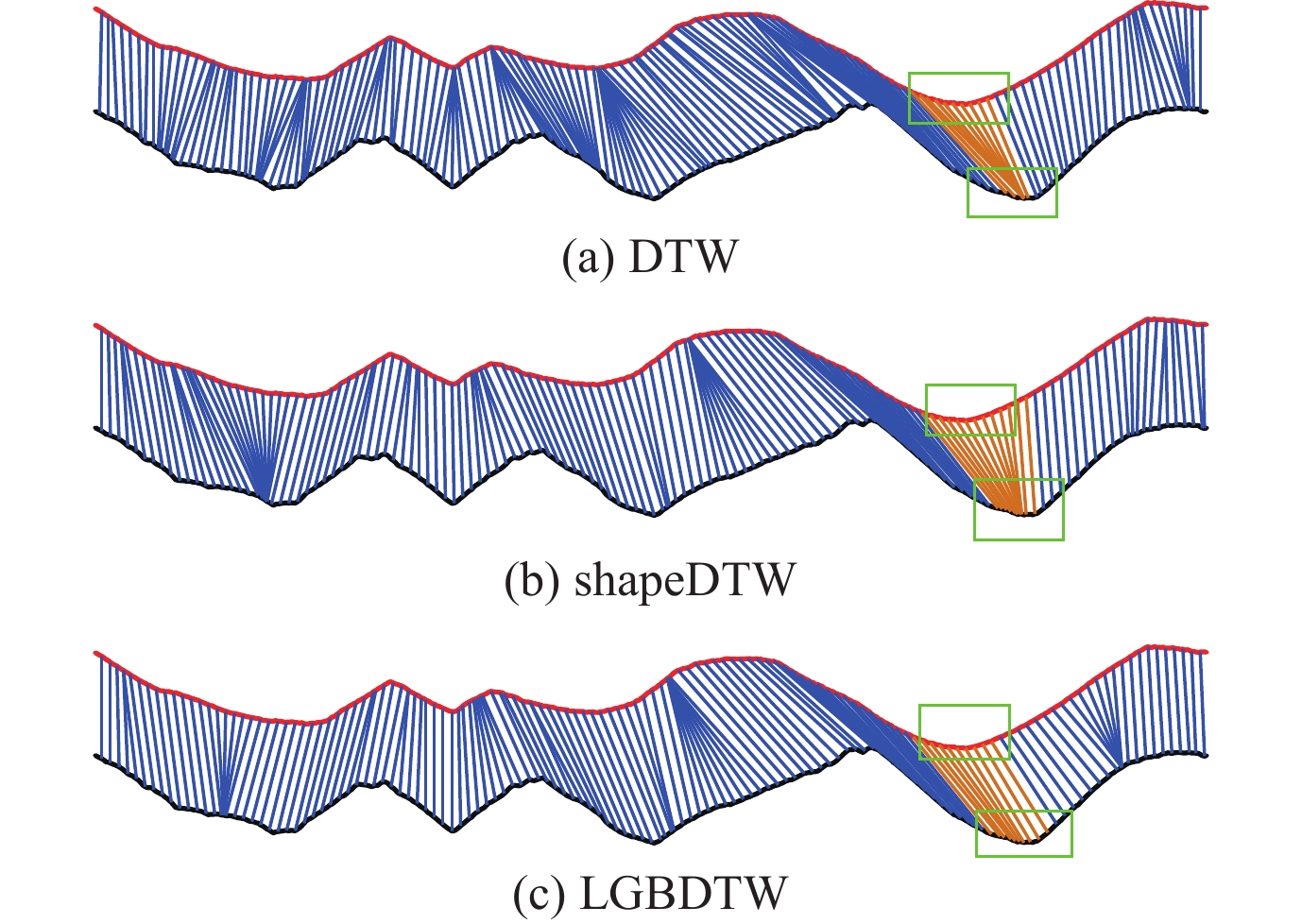
4.4 实例分析BirdChicken是在文献[10]中作者提供的数据集, 该数据集中的序列来分别提取自小鸟和小鸡两种动物的图像轮廓. 对该数据集的分类目的主要是通过图像轮廓序列分类区分小鸟和小鸡. 现有文献中基于距离的分类模型中在该数据集上分类准确率比较高的是shapeDTW模型, 如表1所示, 该模型准确率达到了95%. 然而, LGBDTW在这个数据集上的准确率达到了100%. 图16中展示了BirdChicken数据集中两个同类序列分别使用DTW、shapeDTW以及LGBDTW对齐的效果. 其中每对绿色方框区域表示的是两条序列中具有相似的局部形状结构的部分. 从图中可以看出, DTW、shapeDTW以及LGBDTW在序列的局部形状匹配效果上存在明显的差异. 在绿色方框表示的局部结构匹配过程中, DTW和shapeDTW出现了不同程度的局部对齐错误, 而LGBDTW则实现了较为准确的局部结构对齐, 这表明在同样都能准确分类前提下, 相比于DTW和shapeDTW, LGBDTW具有更好的可解释性, 其分类结果更加可靠.

|
Fig. 15 Comparison of the running time of the classifiers 图 15 分类器运行时间比较 |
|
Fig. 16 Sequences alignment comparison of BirdChicken dataset using DTW, shapeDTW and LGBDTW 图 16 BirdChicken数据集使用DTW、shapeDTW和LGBDTW的序列对齐比较 |
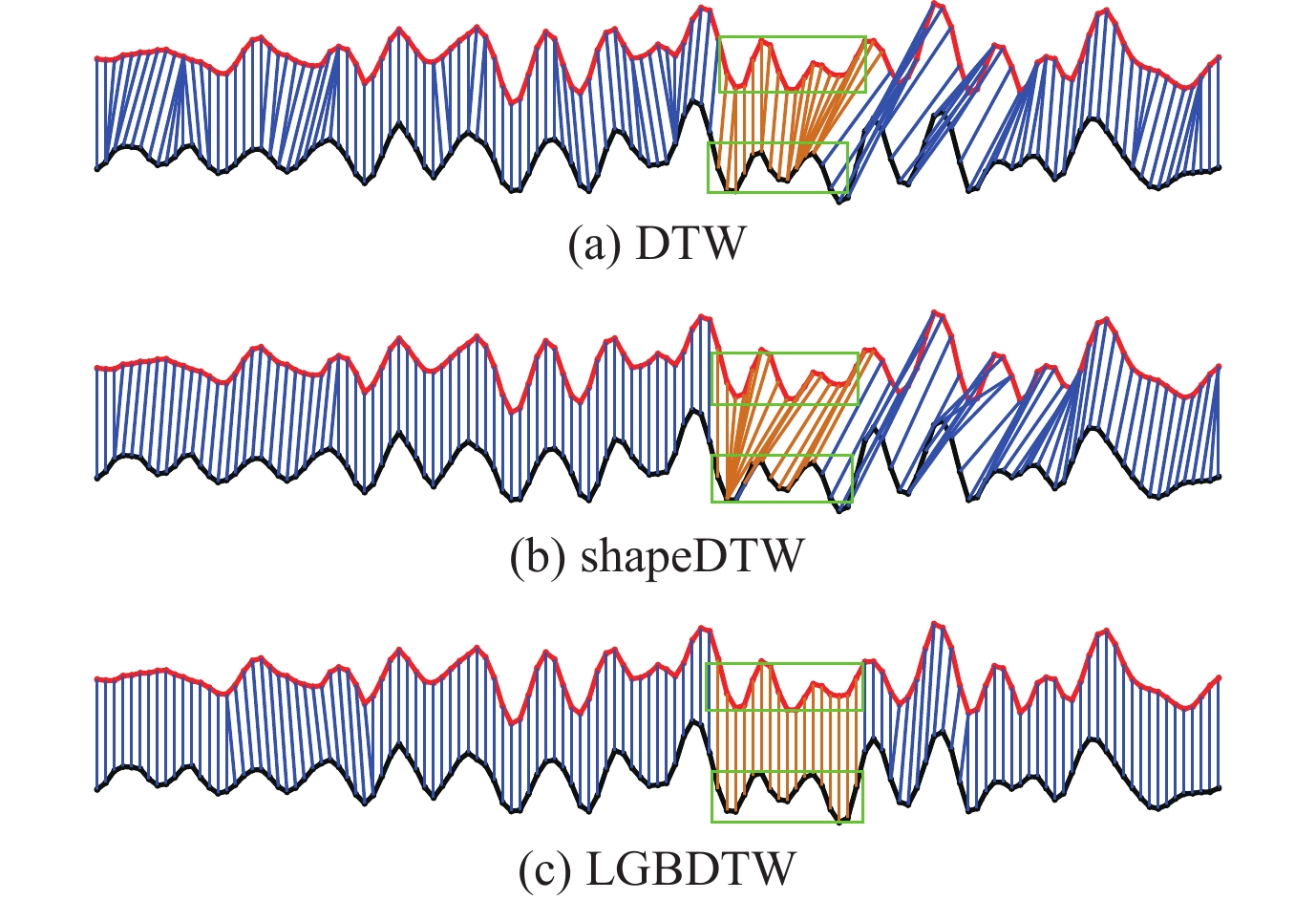
类似的, FacesUCR数据集选取自UCR时间序列数据库, 该数据集序列记录的是不同人的脸部图像轮廓, 其序列分类目的是区分不同人的人脸. 该数据集的特点是其数据序列中包含了多个起伏明显的峰、谷结构, 局部信息丰富. 这里我们同样用该数据集对DTW、shapeDTW和LGBDTW的对齐效果进行了测试. 图17表示的是该数据集中来自同一人的两条脸部轮廓序列采用这3个模型时的对齐结果. 如图中所示, 在绿色方框标注的序列局部结构中, 可以看到, 使用DTW和shapeDTW的序列对齐过程中存在明显的对齐错误. 相反的, 类似于BirdChicken数据集, LGBDTW实现了该部分局部结构的准确对齐, 同样表现出了较好的可解释性, 这表明LGBDTW在该数据集上可以实现更加可靠的分类.
|
Fig. 17 Sequences alignment comparison of FacesUCR dataset using DTW, shapeDTW and LGBDTW 图 17 FacesUCR数据集使用DTW、shapeDTW和LGBDTW的序列对齐比较 |
5 总 结
本文提出了一种基于二进制模式的时间序列局部特征描述子LBPT, 并在此基础上设计了基于LBPT和HOG-1D的时间序列相似性加权度量算法LGBDTW. 相比于传统的基于距离和特征的相似性度量方法, LGBDTW在不明显增加计算复杂性的前提下, 实现了更加精准的时间序列局部结构信息匹配. 此外, 多个数据集上的实验结果表明, 本文所提出的相似性度量算法有效的提升了时间序列的分类准确率, 分类效果较其他的基于距离和基于特征的分类器有明显改善. 同时, 实例分析表明本文算法在可解释性方面也要优于大多数传统分类算法. 关于未来的工作, 我们的研究方向可能包括如何进行LBPT描述子与其他类型特征描述子之间的整合以及探索具有较强时间序列局部信息表示能力的新特征. 同时我们也希望本文所提出的分类算法可以扩展到更多的问题领域.
| [1] |
Zakaria J, Mueen A, Keogh E, Young N. Accelerating the discovery of unsupervised-shapelets. Data Mining and Knowledge Discovery, 2016, 30: 243-281.
[doi:10.1007/s10618-015-0411-4] |
| [2] |
Brill M, Fluschnik T, Froese V, Jain B, Niedermeier R, Schultz D. Exact mean computation in dynamic time warping spaces. Data Mining and Knowledge Discovery, 2019, 33: 252-291.
[doi:10.1007/s10618-018-0604-8] |
| [3] |
Bagnall A, Lines J, Bostrom A, Large J, Keogh E. The great time series classification bake off: A review and experimental evaluation of recent algorithmic advances. Data Mining and Knowledge Discovery, 2017, 31(3): 606-660.
[doi:10.1007/s10618-016-0483-9] |
| [4] |
Berndt D, Clifford J. Using dynamic time warping to find patterns in time series. In: KDD94: AAAI Workshop on Knowledge Discovery in Databases. Seattle: KDD Workshop, 1994. 359−370.
|
| [5] |
Gavrila DM, Davis LS. 3-D model-based tracking of human upper body movement: A multi-view approach. In: Proc. of Int’l Symp. on Computer Vision-ISCV. Coral Gables: IEEE Press, 1995. 272–277.
|
| [6] |
Sakoe H, Chiba S. Dynamic programming algorithm optimization for spoken word recognition. IEEE Trans. on Acoustics, Speech, and Signal Processing, 1978, 26(1): 43-49.
[doi:10.1109/TASSP.1978.1163055] |
| [7] |
Rath TM, Manmatha R. Word image matching using dynamic time warping. In: Proc. of the 2003 IEEE Computer Society Conf. on Computer Vision and Pattern Recognition, 2003. Madison: IEEE Press, 2003. 521–527.
|
| [8] |
Hsu E, Pulli K, Popović J. Style translation for human motion. In: Proc. of the 32nd ACM Int’l Conf. on Special Interest Group on Computer Graphics and Interactive Techniques (SIGGRAPH 2005). Los Angeles: ACM Press, 2005. 1082–1089.
|
| [9] |
Boulnemour I, Boucheham B, Benloucif S. Improved dynamic time warping for abnormality detection in ECG time series. In: Proc. of the 4th Int’l Conf. on Bioinformatics and Biomedical Engineering. Granada: Springer Press, 2016. 242–253.
|
| [10] |
Hills J, Lines J, Baranauskas E, Mapp J, Bagnall A. Classification of time series by shapelet transformation. Data Mining and Knowledge Discovery, 2014, 28(4): 851-881.
[doi:10.1007/s10618-013-0322-1] |
| [11] |
Zhao JP, Itti L. ShapeDTW: Shape dynamic time warping. Pattern Recognition, 2018, 74: 171-184.
[doi:10.1016/j.patcog.2017.09.020] |
| [12] |
Dalal N, Triggs B. Histograms of oriented gradients for human detection. In: Proc. of the 2005 IEEE Computer Society Conf. on Computer Vision and Pattern Recognition (CVPR’05). San Diego: IEEE Press, 2005. 886–893.
|
| [13] |
Ojala T, Pietikäinen M, Maenpaa T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2002, 24(7): 971-987.
[doi:10.1109/tpami.2002.1017623] |
| [14] |
Marteau PF. Time warp edit distance with stiffness adjustment for time series matching. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2009, 31(2): 306-318.
[doi:10.1109/TPAMI.2008.76] |
| [15] |
Stefan A, Athitsos V, Das G. The move-split-merge metric for time series. IEEE Trans. on Knowledge and Data Engineering, 2013, 25(6): 1425-1438.
[doi:10.1109/TKDE.2012.88] |
| [16] |
Deng HT, Runger G, Tuv E, Vladimir M. A time series forest for classification and feature extraction. Information Sciences, 2013, 239: 142-153.
[doi:10.1016/j.ins.2013.02.030] |
| [17] |
Baydogan MG, Runger G, Tuv E. A bag-of-features framework to classify time series. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2013, 35(11): 2796-2802.
[doi:10.1109/TPAMI.2013.72] |
| [18] |
Baydogan MG, Runger G. Time series representation and similarity based on local autopatterns. Data Mining and Knowledge Discovery, 2016, 30(2): 476-509.
[doi:10.1007/s10618-015-0425-y] |
| [19] |
Nguyen TL, Gsponer S, Ilie I, Ifrim G. Interpretable time series classification using all-subsequence learning and symbolic representations in time and frequency domains. arXiv: 1808.04022, 2018.
|
| [20] |
Schäfer P. The BOSS is concerned with time series classification in the presence of noise. Data Mining and Knowledge Discovery, 2015, 29(6): 1505-1530.
[doi:10.1007/s10618-014-0377-7] |
| [21] |
Guennec AL, Malinowski S, Tavenard R. Data augmentation for time series classification using convolutional neural networks. In: ECML/PKDD Workshop on Advanced Analytics and Learning on Temporal Data. Riva Del Garda, 2016.
|
| [22] |
Cui ZC, Chen WL, Chen YX. Multi-scale convolutional neural networks for time series classification. arXiv: 1603.06995, 2016.
|
| [23] |
Wang ZG, Yan WZ, Oates T. Time series classification from scratch with deep neural networks: A strong baseline. In: Proc. of the 2017 Int’l Joint Conf. on Neural Networks (IJCNN). Anchorage: IEEE Press, 2017. 1578–1585.
|
| [24] |
Zhao BD, Lu HZ, Chen SF, Liu JL, Wu DY. Convolutional neural networks for time series classification. Journal of Systems Engineering and Electronics, 2017, 28(1): 162-169.
[doi:10.21629/JSEE.2017.01.18] |
| [25] |
Candan KS, Rossini R, Wang XL, Sapino ML. SDTW: Computing DTW distances using locally relevant constraints based on salient feature alignments. Proc. of the VLDB Endowment, 2012, 5(11): 1519-1530.
[doi:10.14778/2350229.2350266] |
| [26] |
Zhang Z, Tavenard R, Bailly A, Tang XT, Tang P, Corpetti T. Dynamic time warping under limited warping path length. Information Sciences, 2017, 393: 91-107.
[doi:10.1016/j.ins.2017.02.018] |
| [27] |
Keogh EJ, Pazzani J. Derivative dynamic time warping. In: Proc. of the 2001 SIAM Int’l Conf. on Data Mining (SDM). Chicago: SDM Press, 2001. 1–11.
|
| [28] |
Jeong YS, Jeong MK, Omitaomu OA. Weighted dynamic time warping for time series classification. Pattern Recognition, 2011, 44(9): 2231-2240.
[doi:10.1016/j.patcog.2010.09.022] |
| [29] |
Batista GEAPA, Keogh EJ, Tataw OM, De Souza VMA. CID: An efficient complexity-invariant distance for time series. Data Mining and Knowledge Discovery, 2014, 28(3): 634-669.
[doi:10.1007/s10618-013-0312-3] |
| [30] |
Zhao JP, Itti L. Classifying time series using local descriptors with hybrid sampling. IEEE Trans. on Knowledge and Data Engineering, 2016, 28(3): 623-637.
[doi:10.1109/TKDE.2015.2492558] |
| [31] |
Xu Q, Yang J, Ding SY. Texture segmentation using LBP embedded region competition. Electronic Letters on Computer Vision and Image Analysis, 2005, 5(1): 41-47.
[doi:10.5565/rev/elcvia.83] |
| [32] |
Ahonen T, Hadid A, Pietikainen M. Face description with local binary patterns: Application to face recognition. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2006, 28(12): 2037-2041.
[doi:10.1109/TPAMI.2006.244] |
| [33] |
Li SZ, Zhang L, Liao SC, Zhu XX, Chu RF, Ao M, He R. A near-infrared image based face recognition system. In: Proc. of the 7th Int’l Conf. on Automatic Face and Gesture Recognition (FGR06). Southampton: IEEE Press, 2006. 455–460.
|
| [34] |
Satpathy A, Jiang XD, Eng HL. LBP-based edge-texture features for object recognition. IEEE Trans. on Image Processing, 2014, 23(5): 1953-1964.
[doi:10.1109/TIP.2014.2310123] |
| [35] | |
| [36] |
Demšar J. Statistical comparisons of classifiers over multiple data sets. The Journal of Machine Learning Research, 2006, 7: 1-30.
|
| [37] |
Rakthanmanon T, Keogh E. Fast shapelets: A scalable algorithm for discovering time series shapelets. In: Proc. of the 2013 SIAM Int’l Conf. on Data Mining (SDM). Austin: SIAM Press, 2013. 668–676.
|
| [38] |
Grabocka J, Schilling N, Wistuba M, Thieme LS. Learning time-series shapelets. In: Proc. of the 20th ACM SIGKDD Int’l Conf. on Knowledge Discovery and Data Mining. New York: ACM Press, 2014. 392–401.
|
| [39] |
Kate RJ. Using dynamic time warping distances as features for improved time series classification. Data Mining and Knowledge Discovery, 2016, 30(2): 283-312.
[doi:10.1007/s10618-015-0418-x] |
| [40] |
Lin J, Khade R, Li Y. Rotation-invariant similarity in time series using bag-of-patterns representation. Journal of Intelligent Information Systems, 2012, 39(2): 287-315.
[doi:10.1007/s10844-012-0196-5] |
| [41] |
Senin P, Malinchi S. SAX-VSM: Interpretable time series classification using SAX and vector space model. In: Proc. of the 13th IEEE Int’l Conf. on Data Mining. Dallas: IEEE Press, 2013. 1175–1180.
|
| [42] |
Serră J, Pascual S, Karatzoglou A. Towards a universal neural network encoder for time series. arXiv: 1805.03908, 2018.
|
| [43] |
Zheng Y, Liu Q, Chen EH, Ge Y, Zhao JL. Time series classification using multi-channels deep convolutional neural networks. In: Proc. of the 15th Int’l Conf. on Web-Age Information Management. Springer, 2014. 298–310.
|
| [44] |
Tanisaro P, Heidemann G. Time Series classification using time warping invariant echo state networks. In: Proc. of the 15th IEEE Int’l Conf. on Machine Learning and Applications (ICMLA). Anaheim: IEEE Press, 2016. 831–836.
|
 2022, Vol. 33
2022, Vol. 33



