随着车联网(Internet of vehicle, IOV)的快速发展, 车辆的智能化服务得以普及, 特别是基于位置的服务(location-based services, LBSs)已广泛地融入到人们的日常生活中, 并为其带来了极大的便利^[1−4]. 车载用户通过提交兴趣点(point of interest, POI)及当前位置, 从LBS提供商那里轻松地获得了基于内容的搜索服务, 如查询当地的天气状况、周围商场和酒店等信息. 然而, 基于位置的应用均需用户提交位置信息, 这将使用户的位置信息被公开, 造成敏感信息的泄露^{[5, 6]}. 因此, 当用户享受LBS提供的服务时, 位置隐私是一个非常重要的安全问题.

现有位置隐私保护方案主要分为以下几类: 加密机制、缓存策略、匿名技术及差分隐私. 匿名利用泛化理论对位置隐私进行保护^[7], 即: 将用户的真实位置与其他k−1个用户的位置一起生成一个匿名区域发送给LBS服务器来保护用户的真实位置信息. 但是由于车辆节点具有高速自主的移动特性, 使得隐私保护水平被削弱, 因此, 匿名方案不能直接应用于车联网中. 基于加密的隐私保护方案^[8]将用户的位置信息通过单向不可逆的加密函数进行处理, 可以在确保服务可用的情况下不泄露用户的身份与位置信息. 但其费用消耗大, 计算复杂度高, 使得数据共享和数据挖掘难以实现. 基于缓存机制的方案^[9]通过减少用户与LBS提供者之间的交互次数, 以降低用户隐私信息泄露的可能性, 然而这些缓存策略很少考虑到用户复杂性的需求. 由此可见, 传统的位置隐私保护方法不能为车载网络提供有效的隐私保障.

由于差分隐私不依赖于攻击者的任何背景知识, 具有很强的隐私性保障^[10], 能够从数据源头彻底切断用户隐私泄露的可能性, 因此近年来越来越多地被引入到车联网中以保护车载用户的位置隐私^{[11, 12]}. Dwork等人^[13]在2006年首次提出了差分隐私这一概念, 该技术主要针对统计数据库的隐私泄露问题被提出, 是一种运用数学推理严格证明的隐私保护模型, 它能够确保尽管攻击者掌握了数据库中除某一条信息以外的其他所有信息, 仍然无法根据其他数据推测出这条信息. 差分隐私的主要思想是: 在发布的原始数据中添加干扰噪声^[13], 生成虚假数据来保护数据中潜在的用户隐私信息. 在基于差分隐私的位置隐私保护中, 通过引入的隐私预算ε的大小来对真实位置进行加噪处理, ε与数据失真程度成反比, ε越小, 表明原始数据中添加的噪声越多, 隐私保护效果较好. 根据差分隐私的串行组合性质^[14], 对用户驾驶路线上的真实服务请求位置添加噪声时, 该机制主要涉及到隐私预算分配的问题. 然而, 现有差分隐私保护机制无法根据用户在不同位置点的隐私需求为其分配合适的隐私预算, 使得对于用户有些位置点的隐私保护过甚, 而有些位置点隐私保护不及, 这仍然会造成用户位置隐私的泄露. 因此, 解决用户在不同位置点隐私保护需求差异性的问题极为必要.

针对上述问题, 本文提出一种基于敏感位置信息的个性化位置隐私保护方案. 该方案可以在保护车载用户隐私的同时, 满足用户个性化的隐私需求. 提高服务质量. 本文研究内容及贡献如下.

(1) 为了从导航推荐路线中选出效用最高的路线, 引入多属性决策理论建立效用模型. 首先定义了一个归一化的决策矩阵来描述导航推荐路线的效率和隐私效果, 然后将用户的隐私偏好整合到该模型中, 建立多属性效用函数来量化不同路由选择的效用, 为用户选择效用最高的驾驶路线;

(2) 为了满足用户个性化的隐私偏好需求, 提出了一种个性化隐私预算分配算法. 考虑到用户的隐私偏好需求, 以距离占比为衡量指标为用户分配合适的隐私预算, 并确定用户能够接受的虚假位置生成范围, 以生成效用最高的服务请求位置. 在满足用户个性化隐私需求的同时, 提高用户的服务质量(quality of service, QoS);

(3) 对本文方案的性能进行评估, 利用相关定理对其隐私与效用性进行证明, 同时, 基于真实数据集, 通过实验仿真来对比本文方案与现有的Shift Route^[15]和ATGD^[16]方法的性能. 结果表明: 在相同的实验环境约束下, 与Shift Route和ATGD相比, 本文方案的服务质量分别提高了25%和8%, 而LBS的精度只受到很小的影响. 结果表明: 本文方案不仅保证了车载用户LBS请求过程中的隐私保护, 而且能够满足用户的个性化隐私需求, 提供更高的服务质量.

本文第1节分析利用差分隐私思想进行位置隐私保护的相关工作. 第2节介绍本文的相关理论知识. 第3节给出本文所提方案的具体思想与相关理论证明. 第4节在仿真中评估该方案的安全性能, 并与其他类似方案进行比较. 最后, 第5节总结本文的工作.

1 相关工作

在车联网中, 基于位置服务的隐私问题已引起人们的广泛关注并进行了多年研究. 研究发现, 差分隐私保护技术能够很好地解决LBS中的位置隐私泄露问题^[10]. 为了更好地完善差分隐私保护机制在位置隐私保护方面的应用, 国内外的学者对此做出了突破性的研究.

Yin等人^[17]提出了一种满足差分隐私约束的位置隐私保护方法, 其主要针对定位数据高分散性和低密度的特点, 通过结合实用性和私密性来建立多层次的定位信息树模型, 并利用拉普拉斯方案对所选数据的访问频率加入噪声. Peng等人^[18]提出了一种在严格的隐私预算下保护多用户位置相关信息的算法, 该算法利用数据发布机制抵御投机性攻击, 通过自适应分割和合并待搜索区域来构造时间敏感的热点, 其在线性时间复杂度下获得与时间相关的热点, 缩短了算法分析大数据的时间. Sarathy等人^[19]提出了一种满足差分隐私的高斯机制, 在边缘设备的车辆互联网络中给LBS系统的位置添加噪声, 使其原始位置发生扭曲. Chen等人^[20]提出了基于随机理论的差分隐私保护方法, 通过对位置数据的噪声分析来发布简单的位置坐标. Xiong等人^[21]提出了一种私有发布算法, 在严格的隐私概念(差分隐私)下对位置数据集进行随机化, 该算法使用私有位置聚类来缩小随机域, 以隐藏用户的准确位置. Andrés等人^[22]提出了地理不可区分性——第一个可以为LBS提供可证明的隐私保证的正式隐私模型, 该模型源自差分隐私的通用版本, 其基本思想是: 向用户的位置添加噪音, 以使距离最远r的任意两个位置产生具有相似分布的观测值. 其提出了一种很好的扰动机制, 利用拉普拉斯噪声, 很好地实现了地理不可区分性. Jiang等人^[23]对车载用户行驶轨迹中一些经常访问的敏感位置执行噪声处理, 从而保护了用户的位置隐私.

但是, 这些传统的差分隐私保护方法为用户不同的服务请求位置提供的是相同级别的隐私保护, 无法以个性化的差分私有方式来回答敏感技术查询. 为此, 个性化的差分隐私(PDP)保护方案被提出. Li等人^[24]提出一种针对重复查询的个性化差分隐私保护方法, 其根据查询用户权限和相同查询次数生成新的隐私保护规范. 通过在查询结果中加入具有不同分布特征的随机噪声, 实现了差异化的隐私保护. Li等人^[25]提出一种个性化范围的敏感隐私保护方案, 它考虑了位置、查询范围和查询内容之间的关系, 并采用地图存储算法方便了二维局部地图的存储, 降低了存储成本. Zhang等人^[15]策略性地将端点转移到附近的端点, 允许移动客户端检索接近原始端点的兴趣点(POIs), 并设计了从这些POIs中选择移位端点的算法, 实现了地理不可分辨性的隐私特性. Feng等人^[26]提出了一种基于差分隐私的个性化数据隐私发布机制, 利用Hilbert曲线来提取轨迹数据在不同时刻的分布特征, 并针对不同分布特征的轨迹提出了个性化的隐私泛化算法. 但是现有的个性化差分隐私保护方案只是简单地将隐私划分为不同的级别, 最终为每个服务位置提供差异性的保护, 而没有考虑到用户个性化属性需求, 无法根据用户的隐私需求为其提供相应的隐私保护, 这仍然会造成位置隐私的泄露.

因此, 为了避免车载用户位置隐私的泄露, 满足用户的个性化隐私保护需求, 本文基于用户在不同服务请求位置差异化的敏感属性需求, 提出了一种个性化的位置隐私保护方案, 该方案可以根据用户在不同查询位置的隐私需求为其分配相应的隐私预算. 具体来说. 本文首先引入多属性决策理论建立效用模型, 并将用户的服务需求整合到该模型中, 以选择效用最高的驾驶路线; 然后, 考虑到用户的隐私偏好需求, 以距离占比为衡量指标为用户分配合适的隐私预算, 并确定虚假位置的生成范围, 以生成效用最高的服务请求位置. 与现有方案不同的是, 该方案通过每个查询位置可能泄露的敏感信息的大小来分配隐私预算. 特别是, 充分考虑了用户在不同查询位置所需的隐私保护程度, 从而在保护用户隐私的前提下提高了服务质量.

2 相关理论 2.1 基本概念及性质 2.1.1 基本定义

定义1(相邻数据集^[13]). 对于属性结构相同的两个数据集D和D′, 两个数据集的对称差记为DΔD′, 对称差数据集的个数记为|DΔD′|, 若|DΔD′|=1, 则称数据集D和D′是相邻数据集.

定义2(ε-差分隐私^[13]). 对于只相差一条记录的数据集D和D′, 即|DΔD′|≤1. 设有随机算法M, Range(M)表示算法M的取值范围, 若算法M在数据集D和D′上任意输出结果O∈Range(M)满足如下关系式:

$ {\rm{Pr}}[M(D)=O]≤{\rm{e}}^{ε}×{\rm{Pr}}[M(D′)=O]$

(1)

则算法M满足ε-差分隐私. 其中, ε表示隐私预算. ε越小, 数据的隐私性越好; ε越大, 数据的可用性越高.

2.1.2 组合性质

差分隐私的基本特性之一是可组合性, 这一位置差分隐私计算的任何序列也都是差异性私有的. 通常, 差分隐私机制的组合有两种类型: 一种是串行组合, 另一种是并行组合.

性质1(串行组合^[14]). 给定数据集D以及一组关于D的差分隐私算法A₁(D), A₂(D), A₃(D), …, A_m(D), 算法A_i(D)分别满足ε_i-差分隐私, 且任意两个算法的随机过程相互独立. 因此, 这些算法组合起来的算法满足$ \sum\nolimits_{i = 1}^m {{\varepsilon _i}} $-差分隐私.

这个性质说明: 当有一个算法序列同时作用在一个数据集上时, 最终的差分隐私预算等价于算法序列中所有预算之和. 在数据集D中, 用一组独立的隐私保护算法A_i对数据集进行隐私保护, 其差分隐私保护算法序列为数据集D提供的隐私保护程度, 取决于所有隐私保护水平之和, 即最终为数据集D提供的隐私保护满足$ \sum\nolimits_{i = 1}^m {{\varepsilon _i}} $-差分隐私.

性质2(并行组合^[14]). 把一个数据集D分成k个集合, 分别为D₁, D₂, …, D_k, 令A₁, A₂, …, A_k是k个分别满足ε₁, ε₂, …, ε_k的差分隐私算法, 则A₁(D₁), A₂(D₂), …, A_k(D_k)的结果满足$ \mathop {\max }\limits_{i \in [1, 2, ..., k]} {\varepsilon _i} $-差分隐私.

每个数据集D_i的处理算法A_i使得其输出结果O_i满足ε_i-差分隐私. 那么该算法构成的组合算法, 对数据集D提供的隐私保护程度取决于算法序列中保护水平最差者, 即数据集D满足max{ε₁, ε₂, …, ε_k}-差分隐私. 这个性质说明: 当有多个算法序列分别作用在一个数据集且多个不同子集上时, 最终的差分隐私等价于算法序列中所有算法预算的最大值.

2.2 噪声机制

定义3(Laplace机制^[27]). 对于一个函数f: D→R^d, 其中, D是数据库, 函数在数据库上执行查询, 返回一个d维矢量. 函数f: D→R^d的L₁-敏感度函数表示如下:

$ S(f) = \mathop {\max }\limits_{{D_1}, D{}_2} ||f({D_1}) - f({D_2})|{|_1} $

(2)

Laplace机制是对确切的数值型查询结果, 添加服从Laplace分布的随机噪声, 使数值型查询结果满足ε-差分隐私. 在Laplace分布中, 记位置参数为0, 尺度参数为b的分布为Lap(b), 那么其概率密度函数为

$ p(x) = \frac{1}{{2b}}{{\text{e}}^{\left( { - \frac{{|x|}}{b}} \right)}} $

(3)

定义4(指数机制^[28]). 设随机算法M输入为数据集D, 输出为一实体对象r∈R, q(D, r)为可用性函数, Δq为函数q(D, r)的敏感度. 若算法M以正比于$ {\text{e}}\left( {\frac{{\varepsilon q(D, r)}}{{2\Delta q}}} \right) $的概率从R中选择并输出r, 那么算法M提供ε-差分隐私保护, 当且仅当以下表达式成立:

$ A(D, q) \propto {\text{e}}\left( {\frac{{\varepsilon q(D, r)}}{{2\Delta q}}} \right) $

(4)

2.3 地理不可区分性

ε-地理不可区分性^[29]是将差分隐私的思想引入到基于地理位置数据提供服务的系统中. 当施加隐私保护到地理上距离相近的两个点时, 这两个点应该有极大的可能生成相同的虚假位置汇报给位置服务器. 其中, 位置集被表示为X, 联合考虑位置间的欧几里德距离r和参数l来决定位置数据的隐私保护水平.

定义5(ε-地理不可区分性). 一个映射机制K在位置集X上满足由参数ε决定的地理不可区分性定义, 当且仅当位置集中任意的两个位置点x和x′满足:

$ K(x, z)≤{\rm{e}}^{εd(x, x′)}K(x′, z), x, x′, z∈X $

(5)

其中, d(⋅)表示两个位置间的欧几里德距离, X代表这个区域的位置集. 在施加了地理不可区分性隐私保护的情况下, 隐私泄露风险被限制在一个确定的范围内, 该范围由距离d(⋅)和参数ε决定. 这种隐私保护机制被称为拥有了εd₂-隐私保证.

由于差分隐私的拉普拉斯机制适用于一维空间, 如果将其应用于二维空间, 则首先需要为连续平面定义一个满足地理不可区分性的连续机制.

定义6(平面Laplace分布^[30]). 给定ε∈R²、实际位置x, 对于任意一个通过机制产生的近似位置z∈R², 其概率密度函数为

$ {D_\varepsilon }(x)(z) = \frac{{{\varepsilon ^2}}}{{2\pi }}{{\text{e}}^{ - \varepsilon d(x, z)}} $

(6)

上式符合以x为中心的平面Laplace分布. 那么, 以x为原点的极坐标形式的概率密度函数为

$ {D_{\varepsilon , \theta }}(\theta ){D_{\varepsilon , R}}(r) = \frac{{{\varepsilon ^2}}}{{2\pi }}r{{\text{e}}^{ - \varepsilon r}} $

(7)

其中, D_{ε, R}(r)符合参数为$ \left( {2, \frac{1}{\varepsilon }} \right) $的Γ分布.

3 个性化位置隐私保护 3.1 问题描述

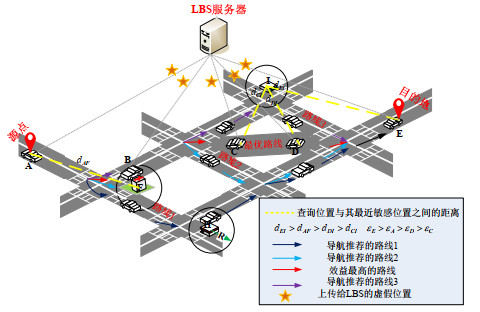
车联网中, LBS系统场景如图 1所示: 车载用户位于A点, 目的地为E点, 用户设置的敏感位置分别为F、H、I. 敏感位置由用户根据需求自行定义, 不同用户会根据自身的需求设置不同的敏感位置点.

在此情况下, 导航系统为用户规划前往目的地的路线总共有4条, 用户首先需要从这些推荐路线中选出效益最高的一条为驾驶路线, 在该路线上, 定期地将服务请求位置更新提交到LBS系统进行服务查询. 然而, 这种频繁的查询将导致敏感信息的泄露, 用户的服务请求位置(A, B, C, D, E)隐私需要得到保护. 显然, 由于这些查询位置(A, B, C, D, E)与其最近敏感位置之间的距离不同, 要想使用户得到高效的服务, 应该为不同查询位置提供不同的隐私保护. 但是, 现有的位置隐私保护无法以个性化的差异私有方式来回答敏感属性查询^{[24, 25]}, 会使对有些位置点隐私保护过甚, 而有些位置点隐私保护不及, 其仍会造成位置隐私的泄露.

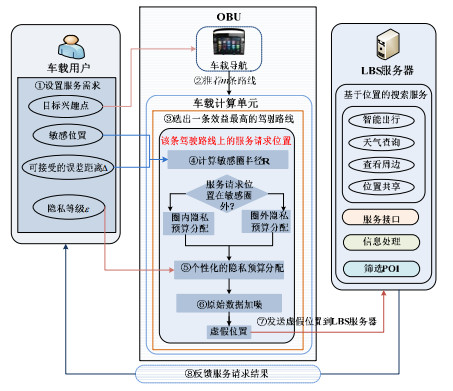
3.2 个性化位置隐私保护

为了解决这一问题, 本文提出了一种基于差分隐私的个性化位置隐私保护方案. 该方案可以根据用户在最优驾驶路线上不同服务请求位置的隐私需求, 为其提供相应的保护. 在进行LBS请求之前, 采用个性化位置隐私保护方案对用户位置信息进行保护, 其具体流程如图 2所示.

1) 车载用户设置其服务需求包括敏感位置点、隐私等级ε、目标兴趣点以及可接受的虚假位置与真实位置的误差距离范围Δ等信息;

2) 车载导航系统根据用户的需求为其推荐m条前往目标兴趣点的驾驶路线;

3) 车载用户根据导航推荐的驾驶路线, 建立出多属性选路效益决策矩阵; 并根据所述多属性选路效益决策矩阵采用信息熵理论的权重分配算法, 建立基于多属性选路效益函数, 该效益函数联合优化了用户在所推荐驾驶路线上源点与目标兴趣点的路程与用户发送的各个请求位置到其最近敏感位置距离之和这两种属性. 根据多属性效益函数计算出所推荐的每条驾驶路线的效益值, 并运用排序算法确定效益最高的路线作为车载用户的驾驶路线;

4) 根据用户在第1步中设定的可接受的误差距离值Δ计算出每个敏感位置点所对应的敏感圈半径R;

5) 基于前面选择的驾驶路线, 按照用户的个性化需求为其分配隐私预算. 判断选定路线上用户的服务请求是否位于敏感圈外, 将位于敏感圈外的每个服务请求位置点依照敏感距离占比分配隐私预算, 将剩余的隐私预算按照均分的方式分配给敏感圈内的每个服务请求位置点;

6) 利用分配给服务请求位置点的隐私预算大小对其进行加噪处理生成虚假位置;

7) 将处理后的虚假位置发送给LBS进行服务请求以保护用户的真实位置信息;

8) LBS根据用户提交的信息为其反馈服务信息结果.

3.3 基于信息熵的多属性决策模型

结合实际情况, 用户所选的驾驶路线主要由两种因素决定: 一是驾驶成本低的路线会被优先选择; 二是隐私泄露更小的路线会被优先选择. 因此, 本节利用车载用户在第k条所推荐的驾驶路线上, 从起始地到目的地的总长度来衡量第k条路线的成本, 若路线总长度越小代表成本越低, 该条路线更容易被选择; 利用车载用户在第k条所推荐路线上所有服务请求位置与其最近敏感位置的距离之和来衡量用户在第k条路线上的隐私泄露度, 若距离越大, 代表隐私泄露都越小, 该条路线更容易被用户选择. 本文建立了一种基于信息熵的多属性决策模型, 综合考虑了路线总长度和服务请求位置与敏感位置的距离这两种属性对路径选择的影响, 对其进行优化, 得到相对最优的道路为用户的驾驶路线. 对于本节所涉及的符号见表 1.

根据多属性决策理论^{[31, 32]}, 属性值与方案被选择的可能性成正比的属性被称为效益属性; 相反, 属性值与方案被选择的可能性成反比的属性被称为成本属性. 在以上两种属性中, 车载用户在第k条所推荐的驾驶路线上所有服务请求位置与其最近敏感位置的距离$ d_{k2}^s $属于效益属性, 第k条所推荐的驾驶路线上从起始地到目的地的距离$ d_{k1}^o $属于成本属性.

定义7(成本属性). 第k条所推荐的驾驶路线中从起始地到达目的地的总长度为

$ d_{k1}^o = \sum\nolimits_{i = 1}^n {\sqrt {{{(x_{i + 1}^k - x_i^k)}^2} + {{(y_{i + 1}^k - y_i^k)}^2}} } , k = 1, 2, ..., m $

(8)

定义8(效益属性). 车载用户在第k条所推荐的驾驶路线上所有服务请求位置点与其最近敏感位置的距离之和为

$ d_{k2}^s = \sum\nolimits_{i, j = 1}^{n, N} {\mu d_{ij}^k} , k = 1, 2, ..., m $

(9)

其中, $ d_{ij}^k $表示在第k条路线上, 第i个服务位置点到第j个位置点的距离值; μ=1代表L_i选择S_j为最近的敏感位置点, μ=0则代表其他情况; N为用户设定的敏感位置总数; m为导航为用户推荐的总路径数.

3.3.1 不同效益属性评价值的规范化

本文考虑了两种属性对路径选择的影响, 即: 第k条所推荐的驾驶路线上所有服务请求位置点与其最近敏感位置的距离之和$ d_{k2}^s $作为效益属性, 用户在第k条驾驶路线上从源点到目标兴趣点的驾驶路线总长度$ d_{k1}^o $为成本属性, 影响用户选哪条路的属性集为$ \{ d_{k1}^o, d_{k2}^s\} $. 由于导航系统为用户推荐了m条驾驶路线, 以此建立多属性效益决策矩阵, 将所推荐的多条驾驶路线分别作为m个方案, 在每个方案(每条路)中包含两个重要属性, 则m个方案可以形成一个m×2的多属性决策矩阵, 形式为

$ D = \left\{ {\begin{array}{*{20}{c}} {d_{11}^o}&{d_{12}^s} \\ \begin{gathered} d_{21}^o \hfill \\ \vdots \hfill \\ d_{m1}^o \hfill \\ \end{gathered} &\begin{gathered} d_{22}^s \hfill \\ \vdots \hfill \\ d_{m2}^s \hfill \\ \end{gathered} \end{array}} \right\} $

(10)

在多属性决策矩阵中, 各个属性的含义和量纲具有差异性, 且具有不可公度性. 同时, 各个属性值都会影响到用户最终的决策结果. 因此, 为了使该决策矩阵的最终结果满足用户的个性化需求, 运用标准化方式来消除各个属性之间的差异性, 对影响路径选择的两种属性进行标准化处理可以表示为

$ {r_{k1}} = \frac{{\max \{ d_{11}^o, d_{21}^o, ..., d_{m1}^o\} - d_{k1}^o}}{{\max \{ d_{11}^o, d_{21}^o, ..., d_{m1}^o\} - \min \{ d_{11}^o, d_{21}^o, ..., d_{m1}^o\} }}, k = 1, 2, ..., m $

(11)

$ {r_{k2}} = \frac{{d_{k2}^s - \min \{ d_{12}^s, d_{22}^s, ..., d_{m2}^s\} }}{{\max \{ d_{12}^s, d_{22}^s, ..., d_{m2}^s\} - \min \{ d_{12}^s, d_{22}^s, ..., d_{m2}^s\} }}, k = 1, 2, ..., m $

(12)

其中, r_k1为成本属性; r_k2为效益属性; m为导航为用户规划的总路径数; r_kj∈[0, 1], k=1, 2, …, m, j=1, 2. 经过无量纲化处理后, 得到规范化矩阵R=(r_kj)_m×2, r_kj称为第k个方案(第k条路)对第j个属性的规范化属性值. 显然, r_kj值越大越好.

根据多属性选路效益函数计算出所推荐的每条驾驶路线的效益值, 并运用排序算法确定效益最高的路线作为车载用户的驾驶路线. 其中, 基于多属性选路效益函数是根据车载用户的成本属性和效益属性计算而得, 其可以表示为

$ z_{k}=w_{1}r_{k1}+w_{2}r_{k2}, k=1, 2, ..., m $

(13)

其中, w₁表示车载用户成本属性采用信息熵理论所分配的权重值, r_k1表示车载用户选择第k条所推荐的驾驶路线的成本属性; w₂表示车载用户效益属性采用信息上理论所分配的权重值, r_k2表示车载用户选择第k2条所推荐的驾驶路线的效益属性; 且满足w₁+w₂=1. 当两个属性的权重值确定之后, 可以通过计算每条路径的效用值确定车载用户选择行驶哪条驾驶路线, 从而进行该条驾驶路线的隐私预算的分配.

3.3.2 不同效益属性的权重分配

属性权值的选择直接影响到决策的结果, 采用信息熵的方法确定决策矩阵的权值. 对于决策矩阵R=(r_kj)_m×2, 方案对于属性j的评价p_ij定义为

$ {p_{ij}} = \frac{{{x_{ij}}}}{{\sum\nolimits_{i = 1}^m {{x_{ij}}} }}, \forall i, j $

(14)

将p_ij带入信息熵计算公式, 则方案关于属性j的熵值E_j为$ {E_j} = - k\sum\nolimits_{i = 1}^m {{p_{ij}}} \ln {p_{ij}}, k = \frac{1}{{\ln m}}, $信息偏差度定义为d_j=1−E_j.

决策过程中, 若用户对某些属性有特殊偏好, 则可引入偏好值λ_l对权重进行调整, 相关权重可以表示为

$ {w_l} = \frac{{{\lambda _l}{d_l}}}{{\sum {{\lambda _l}{d_l}} }}, l = 1, 2 $

(15)

其中, λ_l表示用户对第l个属性值的偏好度; d_l表示真实数据信息与目标数据信息之间的偏差度, 即d_l=1−E_l. 上述公式满足0≤w_j≤1, w₁+w₂=1. 当属性权重确定后, 可以通过计算每条路的效用值确定用户选择哪条路, 进而进行隐私预算分配. 算法1概括了基于信息熵的多属性路径效益算法.

算法1. 基于多属性的路径效益算法.

输入: 导航系统为用户推荐的到达目的地k条路线的集合$ R = \{ (x_1^k, y_1^k), (x_2^k, y_2^k), ..., (x_n^k, y_n^k)\} ; $敏感位置集合$ S = \{ (x_1^s, y_1^s), (x_2^s, y_2^s), ..., (x_n^s, y_n^s)\} ; $

输出: 效益函数值最高的路线$ R_{\max }^k. $

1: 计算每条驾驶路线的长度:

$ d_{k1}^o = \sum\nolimits_{i = 1}^n {\sqrt {{{(x_{i + 1}^k - x_i^k)}^2} + {{(y_{i + 1}^k - y_i^k)}^2}} } , k = 1, 2, ..., m; $

2: 计算各路线上每个服务请求位置点与其最近敏感位置点的距离之和

3: 运用公式(11)和公式(12)规范化决策矩阵R=(r_kj)_m×2;

4: 各个属性值权重值的计算: $ {w_l} = \frac{{{\lambda _l}{d_l}}}{{\sum {{\lambda _l}{d_l}} }} $

5: 建立效益函数;

6: index=1

7: for 迭代次数k=1, 2, …, m−1 do

8:     效益函数z_k=w₁r_k1+w₂r_k2, 选择效益函数的最大值

9:         if z[1] < z[k+1] do

10:             z[1]=z[k+1];

11:             index=k+1;

12:         end if

13: end for

14: 获得index, z[index];

3.4 个性化隐私预算分配算法

基于差分隐私的位置隐私保护机制涉及到隐私预算分配的问题, 现有的隐私机制没有考虑到用户的个性化隐私需求, 无法根据用户在不同服务请求点的隐私需求为其分配合适的隐私预算, 使得对于有些位置点的隐私保护过甚, 而有些位置点的隐私保护不及. 因此, 针对车载用户在不同服务请求点隐私保护需求的不同, 在基于选定的驾驶路线下, 提出了一种个性化隐私预算分配PPBA算法, 使得在合理保护用户隐私的条件下, 满足用户个性化的服务需求.

为了满足车载用户在不同服务请求点的隐私需求, 个性化隐私预算分配PPBA算法利用敏感距离占比来量化个性化隐私预算分配模型. 为了使本算法具体实施, 必须对敏感位置点设定敏感区域范围. 若用户的真实位置位于所设置的敏感圈外, 表明实际位置远离敏感位置, 则用户隐私泄露的可能性较小, 隐私预算分配方案可以按照原始方案执行分配过程, 该分配主要由当前服务请求位置点与敏感位置之间的欧几里德距离决定. 显然, 当用户进行服务请求的位置恰好经过敏感位置点时, 若按照这种分配方案进行隐私预算分配, 其隐私预算值接近于0, 则在用户的位置数据上添加的噪声量趋于无穷大, 使得用户获得无效的服务. 针对这种特殊的情况, 提出了敏感圈内部的隐私预算分配方案, 将剩余的隐私预算均匀分配给敏感圈内的所有服务请求位置点. 因此, 本文提出的个性化隐私预算分配PPBA算法能够根据用户在不同位置点的隐私保护需求自适应地为其提供相应的隐私预算, 达到个性化隐私保护的效果. 本小节的隐私预算分配模型主要分为以下几部分: 敏感圈半径R的确定、敏感区域内隐私预算的分配及敏感区域外隐私预算的分配.

3.4.1 敏感圈半径R的确定

采用平面拉普拉斯噪声机制计算出每个敏感位置点所对应的敏感圈的半径. 假设用户当前的真实位置为p₀=(x₀, y₀), 运用平面Laplace机制对实际位置添加噪音处理, 生成的虚假位置为q=(x₀+rrcosθ, y₀+rrsinθ). 用户真实位置与虚假位置之间的失真距离可以表示为

$ rr = ({p_0}, q) = \sqrt {{{(x - {x_0})}^2} + {{(y - {y_0})}^2}} $

(16)

根据地理不可区分性, 运用平面Laplace机制对真实位置加噪处理, 可知rr又有如下关系^[27]:

$ rr = \frac{{ - 1}}{{{\varepsilon _i}}}\left( {{W_{ - 1}}\left( {\frac{{\tau - 1}}{e}} \right) + 1} \right), \tau = rand(0, 1) $

(17)

用户设置自身可以接受的真实位置到虚假位置之间的误差值为Δ, 若要生成的虚假位置满足用户的需求, 则必须满足如下关系:

$ rr≤Δ $

(18)

基于公式(17)及公式(18), 有如下关系:

$ \begin{gathered} \frac{{ - 1}}{{{\varepsilon _i}}}\left( {{W_{ - 1}}\left( {\frac{{\tau - 1}}{{\text{e}}}} \right) + 1} \right) \leqslant \Delta \Rightarrow \frac{{ - Sum}}{{\varepsilon {d_i}}}\left( {{W_{ - 1}}\left( {\frac{{\tau - 1}}{{\text{e}}}} \right) + 1} \right) \leqslant \Delta , Sum = \sum {{d_{i, j}}} \hfill \\ {\text{ }} \Rightarrow R = \frac{{ - Sum}}{{\varepsilon \Delta }}\left( {{W_{ - 1}}\left( {\frac{{\tau - 1}}{{\text{e}}}} \right) + 1} \right) \leqslant {d_{i, j}} \hfill \\ \end{gathered} $

(19)

其中, R表示敏感圈半径; Sum表示用户在整条驾驶路线上, 所有服务位置点到达与其最近的敏感位置点的距离之和; ε表示车载用户选定的总隐私预算值; Δ表示当前服务位置点与生成的虚假位置之间的距离误差阈值, 其为车载用户自行设定; $ {W_{ - 1}}\left( {\frac{{\tau - 1}}{{\text{e}}}} \right) \in ( - M, - 1) $为Lambert函数, M与τ^[27]的取值有关, τ表示在[0, 1]之间生成的随机数.当实际位置与敏感位置之间的距离小于R时, 运用敏感区域内的隐私预算分配; 否则, 运用敏感区域外的隐私预算分配.

3.4.2 敏感区域外隐私预算分配

当用户的真实位置处于所设置的敏感区域外, 即d_{i, j} > R时, 表明实际位置远离敏感位置, 则用户隐私泄露的可能性较小. 此时, 隐私预算分配方案可以按照原始方案执行分配过程. 该分配方案主要由当前服务请求位置与敏感位置之间的欧几里德距离决定, 如图 1所示. 对于敏感圈外的位置A、C、D、E, 分配模型如下所示:

$ {\varepsilon }_{i(外)}=\frac{\mu {d}_{i, j}}{{\displaystyle \sum _{i=1}^{n}{\displaystyle \sum _{j=1}^{N}\mu {d}_{i, j}}}}\varepsilon $

(20)

其中, ε_i(外)表示敏感圈外第i个服务位置点所分配的隐私预算; ε表示车载用户选定的在该条驾驶路线上进行隐私保护的总的隐私预算值; μ=1代表L_i选择S_j为最近的敏感位置点, μ=0则代表其他情况; d_{i, j}表示第i个服务位置点到第j个敏感位置点的距离; n表示服务位置点总数, N表示用户设定的敏感位置点总数.

显然, 当用户进行服务请求的位置恰好经过敏感位置点时, 若按这种分配方法进行隐私预算分配, 其隐私预算值接近于0, 这也就意味着用户的位置数据中添加的噪声量趋于无穷大, 使得用户得到无效的服务. 因此, 针对这种特殊的情况, 提出了敏感区域内的隐私预算分配方案.

3.4.3 敏感区域内隐私预算分配

若用户的实际位置处于自己所设定的敏感区域内部, 表明此时用户进行服务请求的位置点距离敏感位置比较近, 隐私泄露的可能性非常高. 如图 1所示, B处于以F为中心、R为半径的敏感区域范围内. 在该位置进行服务请求时, 用户的隐私预算分配为该条路径上总的隐私预算值减去所有敏感圈外点的隐私预算值之和. 然后, 将剩余的隐私预算均匀分配给每个服务请求位置点. 若整条路线中含有n个点处于敏感圈内, 则每个服务请求位置点分配的隐私预算为

$ {\varepsilon }_{i(内)}=\frac{\varepsilon -{\displaystyle \sum {\varepsilon }_{i(外)}}}{n} $

(21)

其中, ε表示车载用户设定的在该条驾驶路线上的总的隐私预算值; ε_i(外)表示车载用户在当前驾驶路线上, 位于敏感圈圈外的第i个位置分配的隐私预算值; n表示当前驾驶路线上位于敏感圈内的位置点总数. 算法2概括了个性化隐私预算分配PPBA算法的实现过程.

算法2. PPBA算法.

输入: $ R_{\max }^k;S = \{ (x_1^s, y_1^s), (x_2^s, y_2^s), ..., (x_n^s, y_n^s)\} $; Δ; ε; count=0;

输出: 服务请求位置点隐私预算分配结果ε_i.

1: 计算敏感圈半径: $ R = \frac{{ - Sum}}{{\varepsilon \Delta }}\left( {{W_{ - 1}}\left( {\frac{{\tau - 1}}{{\text{e}}}} \right) + 1} \right) $

2: for 迭代次数i=1, 2, …, n do

3: 判断服务请求位置是否在敏感圈外

4:     if $ d_i^s \geqslant R $ then

5:         敏感圈外隐私预算分配: $ {\varepsilon _{i(out)}} = \frac{{\mu {d_{i, j}}}}{{\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^N {\mu {d_{i, j}}} } }}\varepsilon ; $

6:         所有敏感圈外隐私预算之和: ε_sum=ε_sum+ε_i(out);

7:     else

8:         count=count+1;

9:     end if

10: end for

11: 敏感圈内的隐私预算分配: $ {\varepsilon _{i(in)}} = \frac{{\varepsilon - \sum {{\varepsilon _{i(out)}}} }}{n} $

3.4.4 数据效用性分析

定理1((ε_i, δ)-效用性). D为一个事务数据集, $ \bar D $为个性化位置隐私保护方案保护D之后的结果. 若下式关系成立, 则本方案满足(ε_i, δ)-效用性:

$ \Pr [|Q(\bar D) - Q(D)| \leqslant {\varepsilon _i}] > 1 - \delta $

(22)

证明: 假定空间范围查询Q覆盖了输出域中的n项, Q在数据集上的精确查询结果为$ Q(D) = \sum\nolimits_{i = 1}^n {Q({S_i})} , $其中, S_i表示查询Q覆盖的项, 在噪音数据集$ \bar D $上的查询结果表示为$ Q(\bar D) = \sum\nolimits_{i = 1}^n {(Q({S_i} + {N_i}))} , $ N_i表示添加的噪音. 根据(ε_i, δ)-效用性定义可知, 需证明$ \Pr [|Q(\bar D) - Q(D)| \leqslant {\varepsilon _i}] > 1 - \delta , $其中,

$ |Q(\bar D) - Q(D)| = \left| {\sum\limits_{i = 1}^n {Q({S_i} + {N_i})} - \sum\limits_{i = 1}^n {Q({S_i})} } \right| = \left| {\sum\limits_{i = 1}^n {{N_i}} } \right| \leqslant \sum\limits_{i = 1}^n {|{N_i}|} $

(23)

其中, N_i表示在原始数据中添加的满足平面Laplace分布的噪音, 对于每条|N_i|≤ε_i, 均满足如下关系式:

$ \Pr \left[ {\sum\limits_{i = 1}^n {|{N_i}|} \leqslant {\varepsilon _i}} \right] > 1 - \delta $

(24)

若|N_i|≥ε_i, 则记为一次FALURE, 其发生的可能性如下关系式所示:

$ \Pr [{\text{FAILURE}}] = \int_0^{2{\text{π }}} {\int_R^\infty {\frac{{\varepsilon _i^2}}{{2\pi }}r{{\text{e}}^{ - {\varepsilon _i}r}}{\text{d}}r{\text{d}}\theta } } = {{\text{e}}^{ - {\varepsilon _i}R}}(1 + {\varepsilon _i}R) $

(25)

因此, 成功事件的可能性有如下关系:

$ \Pr \left[ {\sum\limits_{i = 1}^n {|{N_i}|} \leqslant {\varepsilon _i}} \right] > {[1 - {{\text{e}}^{ - {\varepsilon _i}R}}(1 + {\varepsilon _i}R)]^n} $

(26)

根据文献[33]可得:

$ {[1 - {{\text{e}}^{ - {\varepsilon _i}R}}(1 + {\varepsilon _i}R)]^n} \geqslant 1 - n{{\text{e}}^{ - {\varepsilon _i}R}}(1 + {\varepsilon _i}R) $

(27)

其中, $ {\varepsilon _i} = \frac{{{d_i}}}{{\sum\nolimits_{i = 1}^n {{d_i}} }}\varepsilon . $由此可得:

$ {[1 - {{\text{e}}^{ - {\varepsilon _i}R}}(1 + {\varepsilon _i}R)]^n} \geqslant 1 - n{{\text{e}}^{ - {\varepsilon _i}R}}(1 + {\varepsilon _i}R) $

(28)

因此, 可得到该方案满足数据效用性定义.

4 实验与分析 4.1 实验场景 4.1.1 实验数据

实验仿真数据集来自微软的T-Drive项目^[34], 其中包含2008年北京1万多辆出租车一周的轨迹数据. 通过利用包含10 357辆出租车中的部分GPS轨迹数据, 评估本文提出的个性化位置隐私保护方案的性能. 在数据集中, 大约有1 500万个点, 每个点以170 s的间隔进行采样(平均距离约为620 m). 该数据集记录了用户的各种户外运动, 包括购物、运动、上班和回家等. 每个轨迹都由一系列GPS点标记, 这些GPS点包含用户的ID、时间戳和用户的位置(纬度和经度).

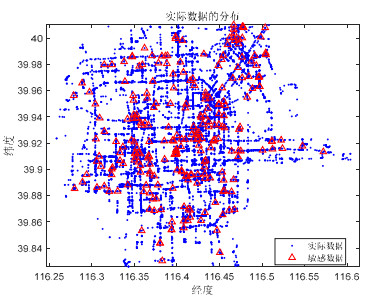
为了验证本文所提个性化位置隐私保护方案的性能, 从T-Drive数据集中抽取出部分数据, 在MATLAB仿真平台进行验证. 图 3是从数据集中抽样出经度值在[116.2, 116.6]、纬度值在[39.8, 40]范围内部分用户的轨迹数据分布情况, 其中, 蓝色的位置点是位置点分布情况. 考虑到每个用户对敏感位置的要求不同, 因此从这些位置分布点中随机抽取部分点, 被标记为红色表示当前区域用户的敏感位置点.

4.1.2 实验方法

本节主要从服务质量与隐私保护两方面来综合评价方案的性能. 由于用户上传给LBS的虚假位置与真实位置之间存在偏差影响了服务质量, 因此, 本文在实验验证时采用服务质量损失来量化用户的服务质量情况.通过计算计数查询Q在经过处理的数据集$ \bar D $与原始数据集D中实际结果的平均相对误差来表示服务质量损失QoS_loss, 平均相对误差可以表示为^[35−38]

$ error(Q(\bar D)) = \frac{{|Q(\bar D) - Q(D)|}}{{\max \{ Q(D), s\} }} $

(29)

其中, $ error(Q(\bar D)) $为经过噪声处理的数据集$ \bar D $与原始数据集D的平均相对误差. 我们以此公式来对服务质量损失进行定义. $ \bar D $表示添加噪音处理之后的数据; D表示原始数据; 参数s是为了防止查询Q的选择性太强而设置的阈值, 以避免分母为0. 所谓查询的选择性是指所有满足查询条件的记录数量占总数的百分比. 其中, max|x|表示查询的最大序列. 当车载用户从LBS提供商获取服务时, 实际位置被虚假位置所代替, 这导致车载用户发送给LBS的服务请求位置偏离了真实位置, 即LBS提供商为用户提供的服务信息不准确. 因此, LBS为车载用户提供的QoS由虚假数据集$ \bar D $与原始数据集D的相似程度决定, 即用户的QoS_loss由平均相对误差$ error(Q(\bar D)) $来决定. 若真实数据集D与噪声数据集$ \bar D $之间的相似度越高, 则QoS越高; 否则, QoS越差.

4.2 隐私效果分析 4.2.1 数据隐私性证明

定理2. 给定用户的真实位置q=(x₀, y₀), 根据分配给该位置的隐私预算为其添加噪声, 然后将生成的虚假位置p发送给服务器. 本文提出的个性化位置隐私保护方案为用户提供了隐私保证, 即, 该方案得到的隐私预算需满足如下关系式:

$ \frac{{{{\Pr }_{{\varepsilon _i}}}(q)(p)}}{{{{\Pr }_{{\varepsilon _i}}}(q')(p)}} \leqslant {{\text{e}}^{{\varepsilon _i}r}} $

(30)

证明: 由定义6可知, 平面Laplace机制的概率函数如下:

$ {D_\varepsilon }({p_0})(p) = \frac{{{\varepsilon ^2}}}{{2\pi }}{{\text{e}}^{ - \varepsilon d({p_0}, p)}} $

(31)

进一步可得如下关系式:

$ \frac{{{{\Pr }_{{\varepsilon _i}}}(q)(p)}}{{{{\Pr }_{{\varepsilon _i}}}(q')(p)}} = \frac{{{{\text{e}}^{ - {\varepsilon _i}d(q, p)}}}}{{{{\text{e}}^{ - {\varepsilon _i}d(q', p)}}}} \leqslant {{\text{e}}^{{\varepsilon _i}[d(q', p) - d(q, p)]}} $

(32)

由于d(q′, p)−d(q, p)≤d(q′, q), 根据地理不可区分性^[28]的基本定义可得d(q′, q)≤r, 由此可以得到:

$ \frac{{{{\Pr }_{{\varepsilon _i}}}(q)(p)}}{{{{\Pr }_{{\varepsilon _i}}}(q')(p)}} = {{\text{e}}^{{\varepsilon _i}[d(q', p) - d(q, p)]}} \leqslant {{\text{e}}^{{\varepsilon _i}d(q, q')}} = {{\text{e}}^{{\varepsilon _i}r}} $

(33)

由此证明了本方案满足ε_i-差分隐私, 可为用户提供可靠的隐私保证. 此外, 下文还分析了本文方案与现有隐私保护机制的比较结果.

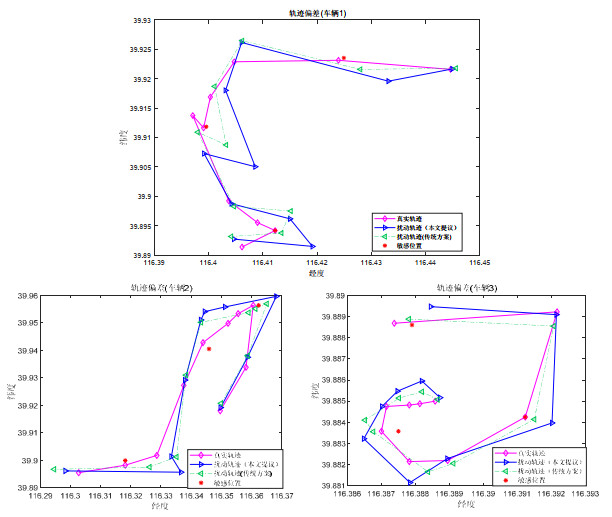
4.2.2 真实轨迹隐私保护验证

在T-Driver数据集的3个经纬度范围内各选取了一个用户, 对用户的真实轨迹进行隐私保护验证. 如图 4所示, 将用户的实际轨迹与本文方案和其他现有机制产生的扰动轨迹进行对比, 验证了该算法对真实轨迹数据的隐私保护效果和服务质量. 由图 4可以看出: 对于靠近用户设定的敏感位置的服务请求位置点, 本文方案提供的隐私保护效果要好于其他方案(本文方案所产生的错误位置距真实位置更远). 对于正常位置(位置距敏感位置较远), 本文方案所生成的虚假位置更接近真实位置, 这可以在合理保护隐私的条件下提高服务质量. 由此可见: 本文提出的方案能够很好地满足用户个性化的隐私保护偏好, 在保护隐私的前提下, 很好地提高服务质量.

4.3 服务质量分析

为了验证本文选路策略的有效性, 第4.3.1节比较了在相同的隐私保护下路径选择对服务质量的影响. 第4.3.2节比较了用户设定的真实位置与虚假位置之间的误差距离Δ对服务质量的影响. 第4.3.3节将本文方案与现有的Shift Route^[15]和ATGD^[16]隐私保护机制进行了比较, 在确定的隐私保护等级下, 验证了它们的服务质量与路径长度的关系.

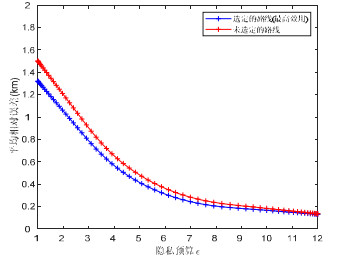
4.3.1 选路与未选路对服务质量的影响

本节比较了利用本文建立的多属性选路效益函数z选择的车载用户驾驶路线与未被选择的驾驶路线对个性化隐私预算分配PPBA算法提供的隐私预算分配产生的服务质量的影响. 由图 5所示结果可以分析看出: 在相同的隐私预算下, 即相同的隐私保护下, 经过本文方案选择的驾驶路线数据服务质量损失明显小于未被选择路线的损失. 因此可以得到: 本文所建立的基于信息熵的多属性决策模型为车载用户提供了更好的服务效用, 为用户推荐了效益最好的路线.

4.3.2 误差值Δ对服务质量的影响

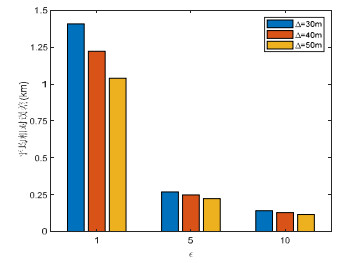
在本小节中, 设定车载用户驾驶的整条轨迹路线的长度为15. 在相同的隐私预算下, 即相同的隐私保护下, 比较了服务质量与用户设定的可接受的虚假位置与真实位置之间的误差距离Δ之间的关系, 由前文分析可得Δ与敏感圈半径成反比关系. 由图 6结果可以分析看出: 在相同的隐私等级下, 即相同的隐私保护下, 服务质量损失与Δ为反比关系. 即: 随着Δ的减小, 敏感圈半径R增大时, 服务质量损失也随之增大. 这主要是因为随着敏感圈半径R的增大, 用户对每个位置点的隐私要求基本相同, 此时, 对一些隐私度要求不高的点也运用了比较高的隐私保护手段, 因此造成了服务质量损失比较大. 而随着Δ的增大, 即敏感圈半径R减小时, 服务质量损失也随之减小. 这主要是因为随着敏感圈半径R的减小, 用户有很明显的敏感位置点隐私需求, 此时只针对一些隐私要求高的点采取更强的隐私保护, 而对于其他位置点则更注重服务质量的提升.

在本实验中, 通过分析比较误差距离Δ与服务质量之间的关系, 得到了敏感圈半径与服务质量为反比关系. 由此验证了本文方案针对敏感位置点采取了很好的隐私保护, 而对于其他位置点, 在保障用户隐私的前提下很好地提高了服务质量(QoS), 能够很好地满足用户个性化的隐私偏好需求.

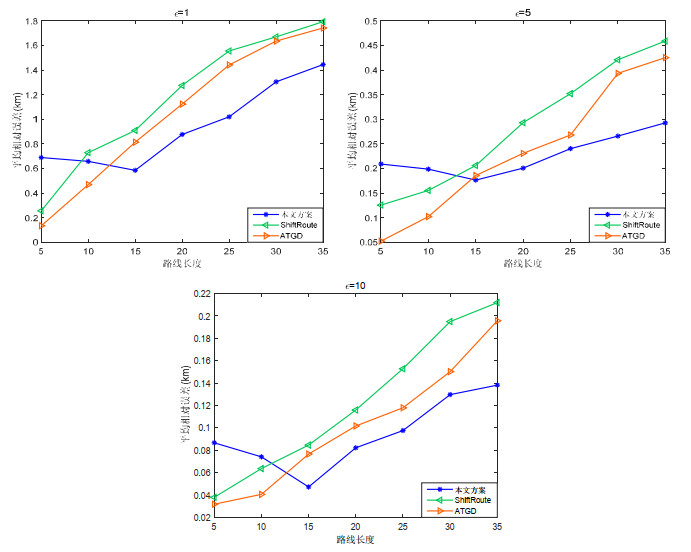
4.3.3 路径长度对服务质量的影响

本节在确定了隐私保护等级后, 比较了用户驾驶路径长度与服务质量之间的关系. 由于用户在选定的最优驾驶路线上行驶时需要定期地将服务请求位置更新提交到LBS系统, 因此本研究利用进行服务请求的位置来表示驾驶路线长度. 从图 7可以分析看出: 在15个服务请求位置之前, 本文方案的隐私保护效果优于ATGD^[15]和Shift Route^[16]这两种隐私保护机制; 而当服务请求的位置数量增加时, 即在15个服务请求位置点之后时, 本文方案的平均误差小于其他两种方案, 从而确保了本方案的服务质量优于其他方案.

通过实验结果可以分析得到: 当所选路由较短(服务请求位置数量较少)时, 则用户设置的敏感位置数量将远大于非敏感位置数量. 由实验结果可以得出, 此时用户的隐私保护效果更好. 这验证了本方案对敏感位置点采取了很好的隐私保护措施. 而在相同数量的敏感位置的前提下选择的路由长度增加时, 则除3个敏感位置外, 非敏感位置数量有所增加. 由实验结果分析得出, 此时本文方案的服务质量高于其他两种方案. 由此可得, 本文方案对于非敏感位置点在保护用户隐私的前提下更侧重于服务质量的提升.

因此, 通过本节实验, 验证了本文方案对于靠近敏感位置的服务请求位置点具有很好的隐私保护效果; 而对于远离敏感位置的服务请求位置点, 在确保隐私的前提下, 能够很好地提高服务质量. 由此可见: 本文方案能够很好地满足用户个性化的隐私偏好需求, 在保护隐私的前提下很好地提高了服务质量.

通过上述从隐私保护与服务质量两方面对本文方案性能的分析, 证明了本文方案能够很好地满足ε_i-差分隐私, 为用户提供了最基本的隐私保证. 通过分析选路与未选路对服务质量的影响, 验证了本文建立的基于信息熵的多属性决策模型为用户推荐了效益最高的路线. 通过对比本文方案与其他方案对于真实轨迹隐私保护效果以及路径长度与服务质量的关系, 验证了本文方案能够很好地满足用户个性化的隐私偏好需求, 在保护隐私的前提下, 很好地提高了服务质量(QoS).

5 结论及展望

为了满足用户的个性化位置隐私保护需求, 本文提出了一种基于差分隐私的个性化位置隐私保护方案. 考虑到路径长度与敏感位置距离对路径选择的影响, 我们首先引入多属性理论来构建效用模型, 然后将用户的个性化服务需求整合到该模型中, 以选择效益最高的驾驶路线. 然后, 根据所选路线上查询位置与其最近敏感位置的距离, 为查询位置分配个性化的隐私预算. 实验结果表明: 与其他已有的位置隐私保护方案相比, 本文方案可以在保护用户隐私的前提下满足其个性化的隐私需求, 提高服务质量.

下一步将对车载用户的其他属性对隐私泄露问题的影响进行分析, 例如驾驶速度、车辆的加速度、驾驶方向等, 以进一步完善车联网中位置隐私保护模型.