随着无人驾驶、无人机、移动机器人等行业的蓬勃发展, 计算机三维视觉逐渐受到学术界与工业界的广泛关注. 作为一个非常庞大的领域, 其可以划分为底层任务、中层任务、高层任务这3个层次.
(1) 底层任务: 包括点云滤波、关键点提取等仅涉及底层信息处理的任务.
(2) 中层任务: 包括特征描述、物体分割等依赖于传统方法对三维物体进行简化、抽象的任务.
(3) 高层任务: 涉及对三维物体和三维场景进行高层次感知和语义理解, 包括物体识别、物体语义分割、场景语义分割等等. 本文主要关注的是计算机三维视觉领域中的高层任务, 重点研究如何更好地识别三维物体, 感知三维场景.
与图像识别类似, 三维物体识别旨在对单个三维物体进行标签分类, 一般需要对物体提取全局性特征, 最后基于该全局特征进行分类处理; 物体语义分割不仅需要对单个三维物体进行分类, 还要能够从语义层面理解物体的各个部位(例如, 飞机可以划分为机头、机身、机翼、机尾等部位), 这就不仅仅需要全局特征, 还需要学习三维物体在不同粒度下的局部特征; 更进一步地, 我们将问题提升至场景语义分割, 需要对包含多个物体的场景进行语义层面的理解, 该问题更加具有挑战性, 同时也更接近于实际应用场景.
由于计算机三维视觉往往应用于无人驾驶、无人机等需要高安全性、高精确度的领域, 现存的方法具有以下局限性.
(1) 对于旋转变换的鲁棒性较差. 目前, 人们已经解决了三维点云的尺度不变性、平移不变性和排列不变性, 但是还有最后一块短板, 即旋转不变性, 尚未在理论和实践层面解决. 同时, 现有的针对点云对抗攻击而提出的防御措施和方法, 包括对抗训练[1−3]、消除离群点[4]、随机采样[5]、加入高斯噪声[5]、量化[5]等, 也只是在特定的对抗攻击如部分点的移动, 删减或增加等条件下提升了模型的鲁棒性和安全性, 对于旋转变换带来的扰动情况尚未进行深入的分析和研究. 我们知道, 三维空间中的旋转变换具有普适性和无穷性, 即每一个三维物体都有无穷种姿态, 我们不可避免地需要应对模型对于旋转变换的鲁棒性问题. 而经过实验表明, 目前的方法在旋转变换的扰动下是脆弱的.
(2) 未充分利用三维点云所蕴含的几何结构、分布特性. 目前的方法基本上采用最远点采样[6]、K维-树[7]、八叉树[8]等启发式方法来设计层次神经网络的结构, 这种结构相当于引入了人类的先验知识去分析三维点云的结构特性. 然而, 在人类先验知识指导下所设计出的层次结构, 并不一定真实地反映了三维点云的几何结构, 这导致现存的层次网络结构在模型容量和表达能力上还有很大的提升空间.
基于以上的考量, 本文的主要工作将试图在两个富有挑战性的方向展开充分的研究: 1) 本文将用数学语言去定义严格旋转不变性映射、K元算子以及映射中的信息损失, 然后运用这一套语言在理论层面上解决三维点云的旋转不变性问题, 并且研究如何应用于现有的模型, 使其能从根本上具有旋转不变性, 从而满足实际应用中所需要的高安全性需求; 2) 本文将探索如何通过机器学习的方法去学习三维点云所蕴含的几何结构, 然后研究如何利用学习到的点云分布特性去自动地指导层次神经网络结构的设计, 提升模型的容量与表达能力, 从而满足实际应用中所需要的高精度需求.
1 三维点云的严格旋转不变性表达为了更加准确地描述严格旋转不变性, 我们用数学语言定义了一种严格旋转不变性映射.
定义1 (严格旋转不变性映射). 给定N, D∈N+, 如果一个点集映射
我们可以看到, 严格旋转不变性映射的定义要求映射具有旋转变换上的不变性. 不仅如此, 映射还需要严格保证输入点集与输出点集在基数上的一致性, 即原本由N个点组成的输入点集必须要被映射为N个点组成的输出点集. 此处正是严格旋转不变性映射的名称中“严格”一词的由来.
基于此定义, 我们会发现: 如果能够找到一种严格旋转不变性映射
定义2 (严格旋转不变性K元算子). 如果一个K元算子
我们可以看到, 严格旋转不变性K元算子严格定义了K个点之间K元关系的一种不变性, 它不受到旋转变换的影响. 基于严格旋转不变性K元算子的定义, 我们可以得到如下引理.
引理1.
(1) 向量L2范数|⋅|2:
(2) 向量内积⋅, ⋅:
(3) 给定任意非零向量p∈
引理1告诉我们, 存在着4种严格旋转不变性算子, 它们分别是向量L2范数、向量内积、
基于这4种严格旋转不变性算子, 我们可以构建出本文所提出的关于三维点云的严格旋转不变性表达, 而计算的过程则为严格旋转不变性映射. 具体而言, 由于三维点云只包含每个孤立的坐标点的信息, 我们首先要对三维点云进行建图. 为了便于将图用张量形式表示, 并且控制每个点的邻居数相同, 本文采用了K-近邻图.
我们首先在三维点云S上建立K-近邻图G=(S, ε), 其中, ε={(x, y)∈S×S|y∈K-NN(x)}. 对于任意的三维点云S={pi∈
| $ \left\{ {\left( {{r_i},\left( {{r_{i1}},{\theta _{i1}},{\phi _{i1}}} \right),\left( {{r_{i2}},{\theta _{i2}},{\phi _{i2}}} \right), \ldots ,\left( {{r_{iK}},{\theta _{iK}},{\phi _{iK}}} \right)} \right){\mathit{\boldsymbol{p}}_i} \in S} \right\} $ | (1) |
其中, 每个变量均为满足旋转不变性的统计量, 其具体的解析表达式为
| $ \left. {\begin{array}{*{20}{l}} {{r_i} = {{\left\| {{\mathit{\boldsymbol{p}}_i}} \right\|}_2}}\\ {{r_{ik}} = {{\left\| {{\mathit{\boldsymbol{p}}_{ik}}} \right\|}_2},(({\mathit{\boldsymbol{p}}_{ik}} \in K{\rm{-}}NN({p_i}),其下标为k)}\\ {{\theta _{ik}} = {\rm{arccos}}\left( {\left\langle {\frac{{{\mathit{\boldsymbol{p}}_i}}}{{{r_i}}},\frac{{{\mathit{\boldsymbol{p}}_{ik}}}}{{{r_{ik}}}}} \right\rangle } \right)}\\ {{\varphi _{ik}} = {\psi _{j * }} \buildrel \Delta \over = {\rm{min}}\{ {\psi _j}\mid 1 \le j \le K,j \ne k\} }\\ {{\psi _j} = \left\{ {\begin{array}{*{20}{l}} {{\rm{a\, tan}}2({\rm{sin}}{\psi _j},{\rm{cos}}{\psi _j}),}&{{\rm{if\, a\, tan}}2({\rm{sin}}{\psi _j},{\rm{cos}}{\psi _j}) \ge 0}\\ {2{\rm{ \mathit{ π} }} + {\rm{a\, tan}}2({\rm{sin}}{\psi _j},{\rm{cos}}{\psi _j}),}&{{\rm{if\, a\, tan}}2({\rm{sin}}{\psi _j},{\rm{cos}}{\psi _j}) < 0} \end{array}} \right.}\\ {{\rm{sin}}{\psi _j} = \left\langle {\frac{{{{\cal T}_{{p_i}}}({\mathit{\boldsymbol{p}}_{ik}})}}{{{{\left\| {{{\cal T}_{{p_i}}}({\mathit{\boldsymbol{p}}_{ik}})} \right\|}_2}}} \times \frac{{{{\cal T}_{{p_i}}}({\mathit{\boldsymbol{p}}_{ij}})}}{{{{\left\| {{{\cal T}_{{p_i}}}({\mathit{\boldsymbol{p}}_{ij}})} \right\|}_2}}},\frac{{{\mathit{\boldsymbol{p}}_i}}}{{{r_i}}}} \right\rangle }\\ {{\rm{cos}}{\psi _j} = \left\langle {\frac{{{{\cal T}_{{p_i}}}({\mathit{\boldsymbol{p}}_{ik}})}}{{{{\left\| {{{\cal T}_{{p_i}}}({\mathit{\boldsymbol{p}}_{ik}})} \right\|}_2}}},\frac{{{{\cal T}_{{p_i}}}({\mathit{\boldsymbol{p}}_{ij}})}}{{{{\left\| {{{\cal T}_{{p_i}}}({\mathit{\boldsymbol{p}}_{ij}})} \right\|}_2}}}} \right\rangle } \end{array}} \right\} $ | (2) |
观察上述解析表达式(2), 我们会发现这些统计量均通过引理1中的4种严格旋转不变性算子计算得出; 同时, 我们提出的严格旋转不变性表达(式(1))还具有非常直观的几何意义. 如图 1所示, 这是一个只包含3个点的三维点云, 我们在该点云上建立了2-近邻图. 在图中, 我们将点描述成向量的形式, 其中标出了向量pi (图 1中的黑色实线箭头)及两个邻居点pi1(图 1中的红色实线箭头)与pi2 (图 1中的蓝色实线箭头). 我们可以看到: ri和rik的几何意义为向量pi与pik的模长; θik的几何意义为向量pi与pik之间的夹角; 而φi1的几何意义为向量pi1经过正交投影之后的投影向量
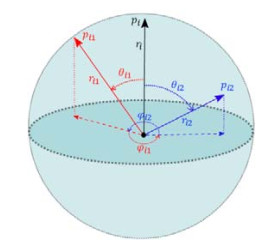
|
图 1 三维点云的严格旋转不变性表达的示意图 |
1.1 严格旋转不变性
我们将上文中各个统计量的解析表达式(2)用算法伪代码的形式描述, 如算法1所示.
算法1. 严格旋转不变性映射.
输入: 点集S⊂ 1: for pi in S do 2: ri←||pi||2 3: for pik in K-NN(pi) do 4: rik←||pik||2 5: 6: 7: for j in [1, k] do 8: 9: 10: if atan2(sinψj, cosψj)≥0 then 11: ψj←atan2(sinψj, cosψj) 12: else 13: ψj←2π+atan2(sinψj, cosψj) 14: end if 15: end for 16: φik←min{ψj|1≤j≤K, j≠k} 17: end for 18: end for 输出: 严格旋转不变性表达
至此, 我们已经介绍了严格旋转不变性表达(式(1))以及严格旋转不变性映射算法1. 下面我们以定理的形式声明其满足严格旋转不变性.
定理1 (严格旋转不变性映射与表达). 给定点集S⊂
如图 2所示, 它直观地表示了本文提出的三维点云具有严格旋转不变性不受任意旋转变换R∈SO(3)的影响. 至此, 我们已经以定理的形式证明了我们提出的三维点云表达(式(1))为严格旋转不变性表达, 而算法1定义了一种严格旋转不变性映射, 使得我们提出的点云表达在旋转不变性上具有理论保障.
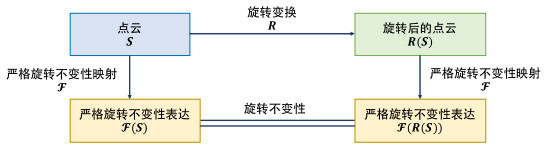
|
图 2 定理1的示意图 |
1.2 信息无损性
尽管严格旋转不变性表达具有我们迫切需要的旋转不变性, 然而, 当我们把三维点云从原始的笛卡尔坐标转化为严格旋转不变性表达的过程中, 很可能会出现信息损失. 这意味着: 我们在追求严格旋转不变性表达的过程中, 有可能会丢失原始表达中蕴含的关键信息. 这会为我们后续的特征提取带来不可逆的信息丢失, 从而影响下游模型的表现与性能.
为了能够严谨定义严格旋转不变性映射及其表达的有损性与无损性, 我们需要引入“旋转可重建性”的概念. 注意, 这个概念与计算机三维视觉领域中的三维重建有着本质不同. 下面我们给出旋转可重建性的定义.
定义3 (旋转可重建性). 给定点集S∈
我们会发现: 重建未知点云R(S)时使用的向量数目k越小, 那么点集映射
为此, 我们需要讨论k点旋转可重建性中k的有效范围. 当k=N时, 点集映射
定理2 (k点旋转可重建性中k的下确界). 对于任意具有k点旋转可重建性的点集映射
定理2符合我们对三维世界的直观感受, 我们可以通过如下朴素的方法来简要证明其正确性. 如果一个三维物体S经过一个未知旋转R, 那么显然旋转后该物体R(S)将会是完全未知的, 因为我们对其姿态一无所知. 现在, 如果我们想要重建出这个未知姿态下的三维物体R(S), 仅仅借助R(S)中一个点的坐标x′是肯定不够的. 我们会发现, 仅仅知道原来三维物体S中的点x旋转后变为x′无法确定旋转后三维物体R(S)的姿态, 因为此时我们还能够以x′为欧拉旋转轴、以任意非零角度进行旋转, 其姿态并不能唯一确定. 因此, 对于任意的三维点云, 不存在点集映射
基于定理2, 我们可以得到如下推论.
推论1 (三维点云的2点旋转可重建性). 假设任意的点云S∈
由定理2及其推论1可知, 当点集映射
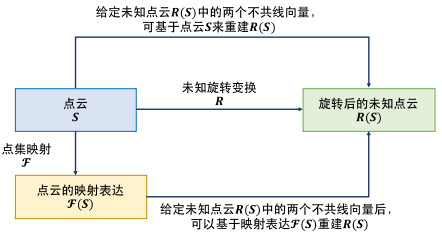
|
图 3 信息无损性的示意图 |
定义4 (信息无损性与条件信息无损性). 如果一个点集映射
基于上述信息无损性与条件信息无损性的定义4, 我们以定理的形式表明: 本文提出的严格旋转不变性映射算法1在不考虑存储空间的情况下是满足信息无损性的, 而在一般情况下满足条件信息无损性.
定理3 (严格旋转不变性映射的信息无损性). 给定点集S⊂
| ${{\mathit{\boldsymbol{p'}}}_j} \in K{\rm{ - }}NN({{\mathit{\boldsymbol{p'}}}_i}).$ |
定理3表明: 本文提出的严格旋转不变性映射以及严格旋转不变性表达在信息损失的角度上是条件信息无损的, 在存储空间不受限制的情况下, 能够实现完全的信息无损性. 这些都为我们所提出的严格旋转不变性表达提供了坚实的理论保障.
1.3 兼容性在本节中, 我们将详细讨论严格旋转不变性表达(式(1))如何具有兼容性, 从而能广泛应用于目前基于三维点云的深度学习算法, 使得在旋转鲁棒性上性能较差的算法也能具有严格旋转不变性, 在需要高安全性、高鲁棒性的实际应用场景中能发挥自己应有的作用.
首先, 目前大多数基于三维点云的深度学习模型采用的输入数据是大小为N×d的矩阵, 其中, N为三维点云中点的数目, d为每个点的维数. 一般情况下, d=3, 即输入数据为N×3的矩阵, 包含三维空间中N个点的笛卡尔坐标; 当然, 有时d > 3, 此时输入数据不仅包含笛卡尔坐标, 还可能包含其他关于点的特征, 例如该点处的颜色、垂直于表面的法向量等等.
第1.1节中介绍的严格旋转不变性表达(式(1))是一个大小为N×(K×3+1)的张量, 如式(3)所示.
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{r_1}}&{({r_{11}},{\theta _{11}},{\phi _{11}})}&{({r_{12}},{\theta _{12}},{\phi _{12}})}& \cdots &{({r_{1K}},{\theta _{1K}},{\phi _{1K}})} \\ {{r_2}}&{({r_{21}},{\theta _{21}},{\phi _{21}})}&{({r_{22}},{\theta _{22}},{\phi _{22}})}& \cdots &{({r_{2K}},{\theta _{2K}},{\phi _{2K}})} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {{r_N}}&{({r_{N1}},{\theta _{N1}},{\phi _{N1}})}&{({r_{N2}},{\theta _{N2}},{\phi _{N2}})}& \cdots &{({r_{NK}},{\theta _{NK}},{\phi _{NK}})} \end{array}} \right] \in {\mathbb{R}^{N \times (k \times 3 + 1)}}} \end{array} $ | (3) |
其中, 第i行表示了三维点云中第i个点所对应的旋转不变性表达, 它是一个大小为N×3+1的张量, 其包含该点的模长ri以及K-近邻点的信息. 第i个点的第i个近邻点, 其信息用三元组(rik, θik, φik)表示.
为了让严格旋转不变性表达(式(3))具有兼容性, 一种朴素的方法是将其重新整理为N×(3K+1)的二维矩阵. 而我们采用的是一种更加巧妙的方法: 将三维点云中每个点的K-近邻域当作子点云进行处理. 由严格旋转不变性表达(式(1))可知, 三维点云中第i个点所对应的旋转不变性表达为
| $ \left( {{r_i},\left( {{r_{i1}},{\theta _{i1}},{\phi _{i1}}} \right),\left( {{r_{i2}},{\theta _{i2}},{\phi _{i2}}} \right), \ldots ,\left( {{r_{iK}},{\theta _{iK}},{\phi _{iK}}} \right)} \right) $ | (4) |
它是一个N×3+1的张量, 我们可以将其中包含的变量进行重新组织, 得到如下形式:
| $ \begin{array}{*{20}{c}}\underbrace {({r_i},{r_{i1}},{\theta _{i1}},{\phi _{i1}})}_{{T_{i1}}},\underbrace {({r_i},{r_{i2}},{\theta _{i2}},{\phi _{i2}})}_{{T_{i2}}},...,\underbrace {({r_i},{r_{ik}},{\theta _{ik}},{\phi _{ik}})}_{{T_{ik}}} \end{array} $ | (5) |
重新组织后, 公式(5)将点i的模长分配给点i的K个近邻, 即放入K个三元组之中, 构成了一个ri, rik, θik, φik组成的四元组. 为了书写的简便性, 我们将这些四元组用Tik表示. 于是, 我们就得到了一个N×K×4的三维张量, 如式(6)所示.
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {({r_1},{r_{11}},{\theta _{11}},{\phi _{11}})}&{({r_1},{r_{12}},{\theta _{12}},{\phi _{12}})}& \cdots &{({r_1},{r_{1K}},{\theta _{1K}},{\phi _{1K}})} \\ {({r_2},{r_{21}},{\theta _{21}},{\phi _{21}})}&{({r_2},{r_{22}},{\theta _{22}},{\phi _{22}})}& \cdots &{({r_2},{r_{2K}},{\theta _{2K}},{\phi _{2K}})} \\ \vdots & \vdots & \ddots & \vdots \\ {({r_N},{r_{N1}},{\theta _{N1}},{\phi _{N1}})}&{({r_N},{r_{N2}},{\theta _{N2}},{\phi _{N2}})}& \cdots &{({r_N},{r_{NK}},{\theta _{NK}},{\phi _{NK}})} \end{array}} \right]} \end{array}\begin{array}{*{20}{c}} { = \begin{array}{*{20}{c}} {({T_{11}})}&{({T_{12}})}& \cdots &{({T_{1K}})} \\ {({T_{21}})}&{({T_{22}})}& \cdots &{({T_{2K}})} \\ \vdots & \vdots & \ddots & \vdots \\ {({T_{N1}})}&{({T_{N2}})}& \cdots &{({T_{NK}})} \end{array} \in {\mathbb{R}^{N \times k \times 4}}} \end{array} $ | (6) |
它通过每个点pi与其K-近邻点之间的旋转不变量{Ti1, Ti2, …, TiK}来表征pi. 由于三维点云中每个点pi的邻域特征往往蕴含于点pi的K-近邻域之中, 严格旋转性表达(式(6))利用了这一特性, 充分挖掘三维点云中每个点的K-近邻域的特征, 并在此基础上, 还满足旋转不变性与条件信息无损性.
此时, 我们可以引入“子点云”的概念. 具体而言, 原本作为输入数据的是一个三维点云, 而三维点云中每个点的K-近邻点集{Ti1, Ti2, …, TiK}也可以视为一个“子点云”, 其中每个点Tik∈R4. 三维点云中每个点所对应的子点云刻画了该点的邻域情况, 包含着重要的邻域信息. 于是, 我们可以采用PointNet[6], 一种在理论上具有通用近似能力的深度学习网络, 来学习每个点所对应的子点云{Ti1, Ti2, …, TiK}的高维嵌入, 从而基于邻域信息更好地表征每一个点, 如图 4所示.
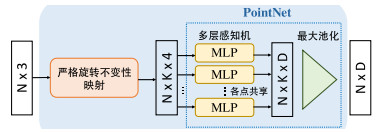
|
图 4 严格旋转不变性表达的兼容性模块的网络结构图 |
综上所述, 我们会发现: 原本N×3的三维点云S, 通过我们提出的严格旋转不变性映射变为N×K×4的严格旋转不变性表达(式(6)). 然后, 我们通过PointNet网络得到N×D兼容性表达. 整个过程相当于是对三维点云中的点pi∈
以动态图卷积神经网络[9]的角度来看, 如图 4所示的神经网络结构可以看作是特殊的边卷积EdgeConv. 然而, 动态图卷积神经网络中的边卷积采用的是中心点pi以及差向量pik−pi去描述中心点pi的第k条边, 其中, pik为pi的第k近邻点. 我们会发现: 无论是中心点还是差向量, 均不具有旋转不变性. 容易证明, 二者均随着旋转变换而改变. 与之不同的是, 我们采用的是严格旋转不变性表达去描述中心点pi与其第k个近邻之间的关系, 即{Ti1, Ti2, …, TiK}, 这种关系与三维点云的姿态无关, 有利于模型聚焦于近邻点之间更加本质的关系.
1.4 时空复杂度分析通过分析算法1可知, 关于K-近邻的计算的时间复杂度为O(NlogN), 关于ri与rik的计算的时间复杂度为O(N), 关于θik的计算的时间复杂度为O(NK), 关于ϕik的计算的时间复杂度为O(NKlogK). 考虑上述所有变量的计算, 严格旋转不变性映射算法的时间复杂度为
而严格旋转不变性映射算法的空间复杂度分析则较为简单. 我们没有使用任何额外的存储空间, 所有变量均有其对应的解析表达式, 故空间复杂度为O(1).
2 层次聚类神经网络 2.1 算法整体框架层次聚类神经网络ClusterNet的整体算法框架总共包含两个阶段.
● 第1阶段是点云几何结构的学习与层次网络结构的生成. 这一阶段是准备阶段, 不涉及模型参数的学习.
● 第2阶段是在第1阶段的基础上进行类簇的嵌入表达学习, 即通过深度学习的方式端到端地学习层次神经网络模型中的待学习参数.
层次聚类神经网络的算法整体框架如图 5所示.

|
图 5 层次聚类神经网络ClusterNet的整体算法框架 |
第1个阶段是对于输入的三维点云S⊂
第2个阶段是类簇的嵌入表达学习阶段, 在这一阶段中, 我们基于上一阶段确定的层次聚类树与层次网络结构, 自底向上地学习层次聚类树中各个类簇的嵌入表达. 具体来说, 类簇的嵌入表达学习包含类簇的边卷积模块与类簇内特征聚合模块, 其中, 类簇的边卷积模块基于类簇的邻域信息来提取类簇的高维特征; 类簇内特征聚合模块负责将父类簇内的若干个子类簇特征进行聚合, 从而得到父类簇的高维特征. 我们通过不断堆叠类簇的边卷积模块与类簇内特征聚合模块, 从而更好地学习整个三维点云的嵌入表达.
2.2 点云几何结构的无监督学习由于现存的层次神经网络在层次结构的设计上往往过度依赖于人类的先验知识, 而这种设计方法都过于启发式, 没有充分地挖掘和利用三维点云本身所蕴含的几何结构与分布特性. 针对这一问题, 本文提出采取基于Ward链接准则[10, 11]的层次聚类算法[12]去学习三维点云本身的层次几何结构. 与其他链接准则不同的是, Ward链接准则没有简单地定义类簇间距离, 而是采用类簇合并前后的类内方差的增加量作为目标函数, 试图最小化因为类簇合并而导致的类内方差的增加, 可以有效地避免类簇聚合中出现某些类簇的规模非常大、而大多数类簇只包含极少的点的极端现象. 为了能够与其他基于类簇间距离的链接准则保持一致, Lance和Williams二人提出了Lance-Williams算法[13], 将其应用到Ward链接准则后, 可以得到类簇间距离的初始化公式与迭代更新公式, 进而可以通过类簇间距离最小化的合并策略去实现基于Ward链接准则的层次聚类算法.
同时, 由于三维点云实际上处于嵌入到三维空间的二维流形之中, 即流形虽然处于三维空间, 但是其本真维度为2. 如果层次聚类算法直接采用三维空间中的欧氏距离作为距离度量, 那么在类簇合并过程中很有可能会出现错误, 把流形中两个并不连通的类簇进行了优先合并, 如图 6(a)所示, 将原本在二维流形中不可达的内层点和外层点错误地归为同一类. 然而, 如果为了避免这一问题而采用本真距离作为距离度量, 则会导致流形上两点之间距离计算的时间复杂度过高, 那么将大大增加距离计算的时间开销.

|
图 6 无连通性约束的层次聚类与有连通性约束的层次聚类在Swiss Roll数据集上聚类的对比示意图 |
为了解决这一问题, 我们采用了具有连通性约束的层次聚类算法. 具体而言, 尽管我们不能直接通过高维空间中的距离度量来计算低维流形中两点的距离, 但是基于流形学习理论, 嵌入到高维空间中的低维流形在局部与欧式空间同胚. 换言之, 低维流形在局部上具有欧式空间的全部性质, 所以可以用欧式距离来计算低维流形上局部两点的本真距离. 因此在实际应用中, 低维流形的局部邻域中两点的欧式距离可以很好地近似本真距离, 即我们可以基于欧式距离来计算近邻点之间的本真距离.
于是, 我们基于欧氏距离去计算三维点云中每个点的K-近邻点集, 即得到三维点云的K-近邻图; 然后, 基于该K-近邻图作为类簇合并时的连通性约束. 在算法的具体实现中, 我们可以通过并查集[14, 15]来表示类簇, 并基于并查集与哈希表, 非常高效地实现类簇的连通性约束, 并且将其应用到基于Ward链接准则的层次聚类算法中, 其伪代码如算法2所示. 图 6(b)展示了有连通性约束的层次聚类在Swiss Roll数据集上的聚类结果, 我们可以看到, 没有出现内层点与外层点被划分为同一类簇的现象, 类簇的划分符合流形上的连通性.
算法2. 有连通性约束的Ward层次聚类算法.
输入: 点集S={p1, p2, …, pN}⊂ 1: for pi in S do 2: Ci←MakeSet(pi) 初始化并查集的初始集合 3: Nodei.cluster←Ci 4: Nodei.left_son←∅, Nodei.right_son←∅ 初始化叶子节点 5: K-NN(Ci)←HashSet({{q}|q∈K-NN(pi)}) 初始化类簇K-近邻 6: end for 7: Ω←DisjointSet({C1, C2, …, CN}) 初始化并查集Ω 8: for i in [1, N−1] do 9: for j in [i+1, N] do 10: d(Ci, Cj)←d(Cj, Ci)←||pi−pj|| 初始化类簇间距离 11: end for 12: end for 13: for t in [1, N−1] do 14: 基于连通性约束搜索距离最近的类簇 15: CN+t←Ω.Unite(Ci*, Cj*) 并查集合并操作, Ω中的Ci*与Cj*被替换为CN+t 16: NodeN+t.cluster←CN+t 17: NodeN+t.left_son←Nodei*, NodeN+t.right_son←Nodej* 创建非叶子节点 18: K-NN(CN+t)←K-NN(Ci)∪K-NN(Cj)\{Ci, Cj} 计算类簇K-近邻 19: for Ck in Ω do 20: if Ci∈K-NN(Ck) or Cj∈K-NN(Ck) then 21: K-NN(Ck)=(K-NN(Ck)\{Ci, Cj})∪{CN+t} 22: end if 23: end for 更新受合并操作影响的类簇的K-近邻 24: for Ck in Ω\CN+t do 25: 26: d(CN+t, Ck)←d(Ck, CN+t)←αid(Ci*, Ck)+αjd(Cj*, Ck)+βd(Ci*, Cj*) 27: end for 计算合并后新类簇与其他类簇的距离 28: end for 输出: 层次聚类树的根节点C2N−1.
现存的基于三维点云的层次神经网络, 其网络结构大多依赖于点云采样[16]、K维树[7]等传统数据结构去构建层次结构. 这种网络结构的设计方式过于启发式, 因为其完全依赖于人类的先验知识, 而没有主动去学习三维点云本身所蕴含的几何结构.
在第2.2节中, 我们详细讨论了如何通过基于连通性约束与Ward链接准则的层次聚类算法去学习三维点云的几何结构, 即得到一棵记录类簇聚合全部过程的层次聚类树. 于是, 我们可以基于从三维点云中学习到的层次聚类树来自动生成层次神经网络的结构. 具体而言, 我们使用含参数的层次神经网络结构的生成方法.
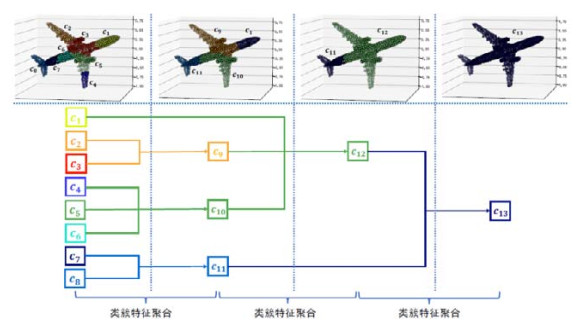
这里的参数是指类簇数目的列表[M1, M2, …, MT], 这意味着我们会将层次聚类过程分为T个阶段, 列表中的Mt代表着第t阶段将当前的Mt−1个类簇聚合为Mt个类簇(令初始类簇的数目为N=M0). 换言之, 层次聚类算法原本会合并N−1. 次类簇(包含N个点的三维点云), 但是我们通过传入的参数列表[M1, M2, …, MT]将整个合并过程划分为T个不同的阶段, 其中每个阶段会包含若干个合并类簇的操作, 而且每个阶段最终都会合并为参数所指定的类簇数目. 由于T ≪ N, 且每个阶段中多个合并类簇的操作可以一次性完成, 所以含参数生成方法的聚合效率与可并行性均远远优于无参数的生成方法. 如图 7所示, 我们以一个飞机的三维点云作为例子, 更加形象地展示了含参数的生成方法.
|
图 7 基于含参数的生成方法来生成层次神经网络结构的示意图 |
2.4 类簇的嵌入表达学习 2.4.1 类簇的边卷积模块
原始的边卷积层[9]只适用于学习三维点云中每个点的嵌入表达, 无法直接应用于层次聚类树中各个类簇的嵌入表达学习. 将边卷积拓展为适用于类簇特征的形式, 其难点在于如何定义类簇集合上的图, 即类簇间的边的关系. 于是, 我们提出两种方法来定义类簇之间的边集.
● 基于层次聚类算法中的类簇间距离: 如算法2中第24−27行所示, 基于Ward链接准则的层次聚类算法会根据Lance-Williams公式计算类簇间距离, 我们可以将其作为类簇间的距离度量, 建立类簇的邻域关系(例如K-近邻关系), 然后将每个类簇Ct与其邻居类簇建立边的关系εt. 于是, 我们就得到了类簇集合上的图G=(Ω, ε), 其中, Ω={Ct|1≤t≤T},
● 基于类簇特征的距离: 基于层次聚类算法中的类簇间距离, 本质上还是基于输入空间
基于上述方法确定了类簇集合上的图结构, 那么类簇集合上的边卷积就非常简单了. 假设在层次聚类树
的某一层, 层次聚类算法将三维点云S={pi∈
| $ \left\{ {\begin{array}{*{20}{l}} {{f_i}' = \mathop {\max }\limits_{j:\left( {i,j} \right) \in \varepsilon } {e_{ij}}}\\ {{e_{ij}} \buildrel \Delta \over = \left( {{{\hat e}_{ij}}} \right) = {h_\mathit{\Theta }}\left( {{f_i} \oplus \left( {{f_j} - {f_i}} \right)} \right)} \end{array}} \right. $ | (7) |
其中,
基于第2.3节得到的索引列表children, 我们就可以定义一种索引池化层(indexed pooling layer)来进行类簇特征的聚合. 顾名思义, 它与一般的池化操作不同的是, 索引池化层并不是对于所有特征都进行特征聚合, 而是根据索引列表对于指定的特征进行池化操作. 具体地, 父类簇Ck的类簇特征, 其计算公式如下.
| $ \begin{array}{*{20}{c}} {{f_k} = \mathop {pooling}\limits_{i \in children[k]} {f_i}} \end{array} $ | (8) |
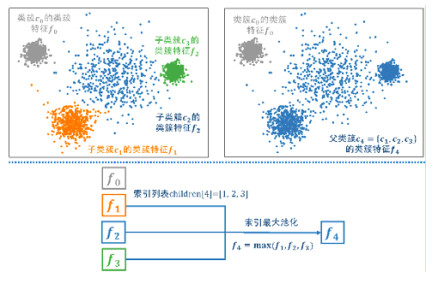
其中, fi为类簇Ci所对应的类簇特征; pooling为具有排列不变性的池化函数, 一般会采用最大池化或平均池化. 显然, 我们会发现: 索引池化层其实是最大池化层或平均池化层的一般性框架, 它试图以索引的形式指明池化的对象. 当索引列表包含所有特征的索引时, 索引列表则退化为普通的池化层, 即最大池化层、平均池化层均为索引池化层的一种特例. 图 8详细展示了索引池化操作的实现细节: 第1行将类簇{c1, c2, c3}的聚合过程可视化; 第2行形象地展示了与第1行相对应的索引最大池化操作, 通过索引列表children[4]=[1, 2, 3], 将子类簇特征{f1, f2, f3}聚合为父类簇特征f4.
|
图 8 索引池化操作的示意图 |
2.5 模型实现细节 2.5.1 类簇特征提取模块(cluster abstraction)
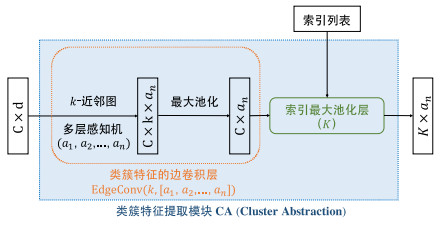
基于第2.4.1节与第2.4.2节介绍的类簇边卷积层与索引池化层, 我们可以将二者相结合, 构成如图 9所示的类簇特征提取模块(cluster abstraction), 我们将其简称为CA模块. 如图 9所示, 类簇特征提取模块由边卷积层与索引最大池化层组成, 整个模块的输入是C×d的输入张量, 其表示三维点云中C个类簇的类簇特征, 特征维度为d; 而输出的是一个K×an的张量, 即我们从C个子类簇的特征中学习到K个父类簇的特征.
|
图 9 类簇特征提取模块的网络结构图 |
2.5.2 点云分类任务的网络结构
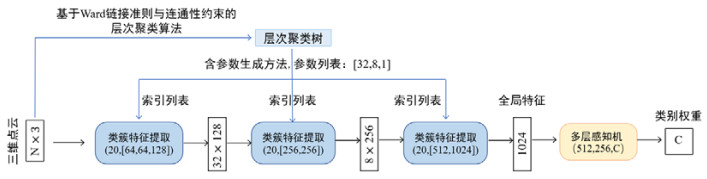
对于点云分类任务而言, 我们的模型需要学习三维点云的全局特征, 然后从全局特征中提取用于分类预测的类别权重. 具体的, 从图 10中我们可以看到, 点云分类任务下的层次聚类神经网络结构可以分为以下4个部分.
|
图 10 三维点云分类任务下, 层次聚类神经网络的网络结构图 |
(1) 首先, 通过第2.2节中介绍的层次聚类算法来学习三维点云的几何结构, 即得到一棵层次聚类树.
(2) 基于第2.3节介绍的含参数生成方法来确定层次神经网络的结构, 其参数为[32, 8, 1]. 于是, 我们就可以得到类簇特征的聚合过程, 且聚合过程可以通过索引列表来实现, 如图 7所示.
(3) 基于索引列表, 我们可以确定类簇特征提取模块(cluster abstraction), 然后通过不断堆叠该模块, 从若干子类簇特征中提取父类簇特征, 直到获得整个三维点云的全局特征.
(4) 由于全局特征综合了整个三维点云的信息, 所以我们可以通过一个三层感知机, 将点云的全局特征转化为用于分类预测的类别权重.
2.5.3 点云分割任务的网络结构对于点云语义分割任务而言, 我们的模型不仅需要学习三维点云的全局特征, 还需要学习各层次下的局部特征, 并且结合所有特征预测三维点云中每个点的类别权重.
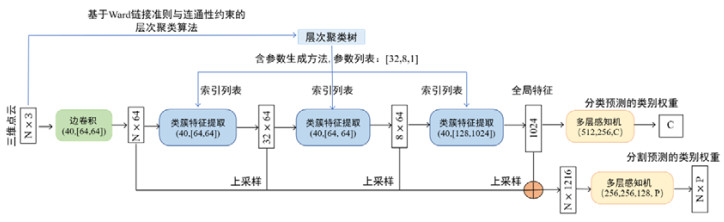
如图 11所示, 层次聚类神经⽹络在点云语义分割任务下的网络结构建立在点云分类任务的基础之上, 它把点云分类任务中由3个类簇特征提取模块(CA)构成的网络结构作为骨干网络, 用来提取点云在不同层次下的类簇特征. 具体而言, 从图 11中我们会发现, 点云语义分割任务下的层次聚类神经网络结构可以分为以下6个部分.
|
图 11 三维点云语义分割任务下, 层次聚类神经网络的网络结构图 |
(1) 首先, 我们会通过第2.2节中介绍的层次聚类算法来学习三维点云的几何结构, 即得到一棵层次聚类树, 这一步与点云分类任务一致.
(2) 基于第2.3节介绍的含参数生成方法来确定层次神经网络的结构, 其参数与点云分类任务相同, 得到表征类簇特征聚合过程的索引列表.
(3) 基于索引列表, 我们可以确定类簇特征提取模块(CA)中的索引最大池化层. 在点云语义分割任务中, 我们采用了更大的K-近邻域, 将点云分类任务中采用的K=20提升至K=40.
(4) 与分类任务不同的是, 我们还在网络最开始阶段加入了一个边卷积模块, 用来提取三维点云中的点特征, 它只包含每个点的K-近邻域信息, 而不包含类簇的信息. 需要注意的是: 边卷积模块所采用的图结构与类簇特征提取模块保持一致, 均为40-近邻图.
(5) 我们将3个CA模块提取到的类簇特征进行上采样操作(up-sampling), 得到与三维点云中点的数目相同的类簇特征, 即三维点云中的每个点都得到其所属类簇的类簇特征, 然后我们就可以将边卷积提取到的点特征与经过上采样的3个类簇特征进行拼接(如图 11中的⊕所示), 于是, 三维点云中每个点都得到了一个1216维的高维嵌入表达.
(6) 最后, 我们可以通过一个含有随机丢失层Dropout[17−19]的四层感知机, 将三维点云中各点的嵌入表达转化为用于分割预测的类别权重, 其中, 每个神经元的丢失概率为drop_rate=0.5.
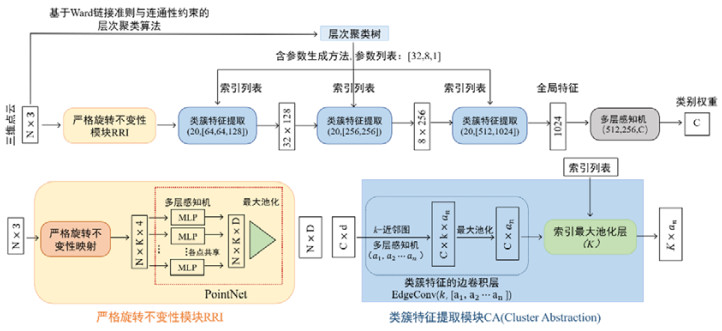
2.5.4 ClusterNet与严格旋转不变性表达的结合为了使得我们的模型具有严格旋转不变性, 我们需要将本节中提出的层次聚类神经网络与第1节中提出的严格旋转不变性映射算法进行结合. 在第1.3节中, 我们介绍了严格旋转不变性表达具有非常良好的兼容性, 它可以通过如图 4所示的兼容性网络结构, 将N×(3×K+1)的严格旋转不变性表达(式(1))转化为N×D的矩阵形式, 使其能够适用于当前大多数的基于三维点云的深度学习模型. 因此, 我们可以很容易地将严格旋转不变性表达应用于本节所提出的层次聚类神经网络, 具体的网络结构如图 12所示.
|
图 12 在点云分类任务下, 具有严格旋转不变性的层次聚类网络结构图 |
由图 12可知, 层次聚类神经网络与严格旋转不变性表达的结合非常简单, 只需要在网络结构的初始阶段加入一个严格旋转不变性模块(RRI)即可. 具体而言: ①在正式进行嵌入表达学习之前, 首先要根据严格旋转不变性映射算法1, 将三维点云转化为严格旋转不变性表达(式(1)), 然后将其重新组织为N×k×4的三维矩阵形式(6); ②然后, 我们将具有通用近似能力的PointNet网络作为基本模块, 即通过各点共享的全连接层与全局最大池化层来学习三维点云中各点的嵌入表达; ③最后则可以将具有严格旋转不变性的嵌入表达传入类簇特征提取模块(CA), 学习在不同层次下类簇的嵌入表达. 我们会注意到, 严格旋转不变性模块RRI得到的是关于点的特征(point feature), 所以三维点云上的k-近邻关系可以对应于点特征之间的k-近邻关系. 因此, 严格旋转不变性表达(式(6))可以直接传入类簇特征提取模块(CA), 即能够兼容于分类任务与语义分割任务下的层次聚类神经网络.
2.5.5 模型训练与测试的方法(1) 点云分类任务下, 模型的训练与测试方法
在点云分类任务中, 我们可以通过层次聚类神经网络的前向传播得到预测分类的类别权重, 我们不妨将其记为x∈
| $ \begin{array}{*{20}{c}} {L(x,class) = - \log \left( {\frac{{\exp (x[class])}}{{\sum\nolimits_j {\exp (x[j])} }}} \right) = - x[class] + \log (\sum\nolimits_j {\exp (x[j])} )} \end{array} $ | (9) |
其中, x为C维向量, 表示模型对于点云在C种类别下的预测权重; class为点云的正确类别. 我们采用Adam优化器[20]来更新网络参数, 设置初始学习率为0.01, 每20轮(epoch)训练衰减为原来的0.7倍, 并且学习率的衰减下界为1×10−5. 整个训练阶段, 共训练250轮(epoch), |Batch|=32. 为了通过并行化计算来提高训练效率, 我们使用了一张12G的NVIDIA TitanX显卡进行训练.
在测试阶段, 我们取权重最大的类别argmax(x)作为模型预测的类别, 然后计算模型在整个测试集上的分类准确率(accuracy), 即点云预测正确的数目与测试集大小的比值.
(2) 点云语义分割任务下, 模型的训练与测试方法
由图 11可知, 我们可以通过层次聚类神经网络的前向传播, 既可以得到预测分类的类别权重向量
对于同时包含分类与分割的真实类别的训练集, 我们采用的损失函数由分类交叉熵损失函数与分割交叉熵损失函数组成, 具体如式(10)所示.
| $ \left. {\begin{array}{*{20}{l}} {{\cal L} = {{\cal L}_{cls}} + {{\cal L}_{seg}}}\\ {\begin{array}{*{20}{c}} {{{\cal L}_{cls}} \buildrel \Delta \over = L(x,clas{s_{cls}}) = - \log \left( {\frac{{\exp (x[clas{s_{cls}}])}}{{\sum\nolimits_j {\exp (x[j])} }}} \right)} \end{array}}\\ {{{\cal L}_{seg}} \buildrel \Delta \over = \frac{1}{N}\sum\nolimits_{i = 1}^N {{\cal L}({X_{ro{w_i}}},clas{s_{seg}}[i])} = - \frac{1}{N}\sum\nolimits_{i = 1}^N {\log \left( {\frac{{\exp ({X_{i,clas{s_{seg}}[i]}})}}{{\sum\nolimits_j {\exp ({X_{ij}})} }}} \right)} } \end{array}} \right\}$ | (10) |
其中, classcls为点云分类的真实类别, 由一个整数表示; classseg为点云分割的真实类别, 由一个N维整数向量表示, 因此, classseg[i]为点云中第i个点的真实类别;
我们同样采用Adam优化器[20]更新网络中的参数, 其中, 初始学习率设置为1×10−2, 并随着训练轮数增加而指数衰减, 衰减步长为20个epoch, 衰减率为0.5, 且衰减下界为1×10−5. 总计150个Epoch, |Batch|=32. 我们采用了两块12 GB的NVIDIA TitanX显卡进行训练.
在测试阶段, 得到预测语义分割类别的权重矩阵X, 然后对每个点pi取权重最大的类别
在本节中, 我们将进行与点云分类任务有关的实验, 比较我们的方法与其他先进方法在该任务下的性能差异. 首先, 我们将详细介绍外部对比实验的具体设置, 包括数据集及其预处理方法、评价方法的设计以及数据集SO(3)增强的具体实现. 我们进行了外部对比实验, 比较我们的方法与其他先进方法在旋转鲁棒性上的性能表现.
3.1.1 实验设置(1) 数据集介绍
在点云分类任务的实验中, 我们采用了被广泛使用的ModelNet40[21]作为基准数据集. 如表 1所示, ModelNet40数据集包含12 311个CAD物体模型, 共分为40种不同的物体类别, 其中, 9 843个模型作为训练集, 剩下的2 468个模型用于测试集.
| 表 1 ModelNet40物体分类数据集 |
ModelNet40数据集中的CAD物体模型, 是一种Mesh数据形式, 由描述物体表面的若干三角形面组成, 其中记录了所有三角形面的顶点坐标. 为了从CAD模型中采样出三维点云, 我们按照Charles R. Qi等人[6]的方法, 根据每个三角形面的面积与物体表面积之比作为采样概率, 在全体三角形面上进行采样. 这意味着: 面积更大的三角形面具有更高的采样概率, 采样点的数目会更多. 为了与现存方法保持一致, 我们选取采样点数目为1 024, 即得到1024×3的三维点云数据.
考虑到模型对于点云扰动的鲁棒性, 我们在训练阶段, 对训练集中的三维点云进行了预处理工作, 其依次分为4个步骤.
1) 点云归一化: 将三维点云的重心平移到笛卡尔坐标的原点, 然后将平移后的点云进行尺度放缩, 把点云约束为半径为1的球体中.
2) 点云随机扰动: 给三维点云中的每个点的笛卡尔坐标(x, y, z)加上一个随机向量(dx, dy, dz)进行扰动, 其中, dx, dy, dz均服从截断高斯分布, 均值为0, 方差为0.01, 截断值为0.05, 即
−0.05≤max(dx, dy, dz)≤0.05.
3) 点云随机放缩: 在[0.8, 1.25]上的均匀分布中进行采样, 得到放缩尺度α∈
4) 点云随机平移: 在[−0.1, 0.1]上的均匀分布中进行3次采样得到平移向量m∈
(2) 模型的评价方法
我们设计了一种新的评价基准来衡量不同模型在三维旋转鲁棒性上的表现. 为了更加全面地评估模型的旋转鲁棒性, 我们采用了3种评价方法, 如下所示.
1) z/z: 这是目前大多数点云感知工作所采用的评价方法. 在训练阶段, 训练集中的三维点云需要经过额外的预处理, 即沿着z轴(笛卡尔坐标系)旋转随机角度. 在测试阶段, 我们首先在区间[0, 2π]上均匀采样60个旋转角, 将测试集中的每个点云沿着z轴旋转对应的角度, 得到60个不同姿态下的新点云; 最后, 我们使用增强后的测试集来测试模型的分类准确率.
2) z/SO(3): 在训练阶段, 与步骤1)保持一致. 由于目前绝大多数测试集所包含的三维物体都只有一种固定的姿态, 或者只沿着固定的欧拉轴旋转, 因此在z/SO(3)的测试阶段, 我们不再限制欧拉轴为z轴, 而是对测试集进行更全面的旋转增强, 即首先在三维旋转变换群SO(3)中均匀采样得到旋转变换矩阵, 然后通过矩阵乘法对测试集进行扩充, 最后使用增强后的测试集来测试模型的分类准确率. 为了描述的准确性与简洁性, 我们将这种对于数据集的旋转增强称为SO(3)增强.
3) SO(3)/SO(3): 为了比较的公平性, 我们在训练阶段也加入更加全面的旋转增强, 即训练集在预处理时采用SO(3)群中均匀采样得到的旋转矩阵, 让模型在训练阶段能够学习不同姿态下的三维点云. 测试阶段与步骤2)保持一致, 采用SO(3)增强后的测试集.
关于数据集的SO(3)增强, 可以通过球面均匀采样或者斐波那契网格[22]来得到欧拉轴e, 在区间[0, 2π]上均匀采样得到旋转角θ, 然后将根据如下公式得到对应的旋转变换矩阵:
| $ R = {I_3}\cos \theta + (1 - \cos \theta )e{e^T} + {[e]_ \times }\sin \theta ,{\text{ }}{[e]_ \times } \triangleq \left[ {\begin{array}{*{20}{c}} 0&{ - {e_3}}&{{e_2}} \\ {{e_3}}&0&{ - {e_1}} \\ { - {e_2}}&{{e_1}}&0 \end{array}} \right] $ | (11) |
其中, I3为3×3的单位矩阵, e为欧拉轴, θ为旋转角.
于是, 我们根据该方法实现了三维旋转变换群SO(3)上的均匀采样. 基于这种采样方法, 总共采样了500个欧拉轴与60个旋转角度, 即得到了30 000个在SO(3)群上均匀分布的旋转变换. 然后, 我们通过这些旋转变换对ModelNet40的测试集进行SO(3)增强, 增强后的测试集大小为2468×30000=74040000, 即测试集中的每个点云都进行了30 000种不同的旋转变换, 得到同一个物体在不同姿态下的三维点云.
3.1.2 外部对比实验为了验证层次聚类神经网络在点云分类任务中的优势, 我们通过第3.1.1节中介绍的3种评估方法来比较我们的模型与现有的先进方法在旋转鲁棒性上的性能.
(1) 基准方法
在对比实验中, 我们选取了9种先进方法作为基准方法, 涵盖了三维物体的多种表示形式: 体素网格、多视图、三维点云、球面表达, 而且均代表了目前最先进的方法. 具体包括SubVolSup[23], MVCNN[24], PointNet[6], PointNet(w/STN)[6], PointNet++[16], PointNet++(w/STN)[16], DGCNN[9], DGCNN(w/STN)[9]和Spherical CNN[25]. (w/STN)代表模型使用空间变换网络STN[26].
(2) 对比实验结果及其分析
表 2展示了各算法在ModelNet40数据集上的分类准确率. 由表 2可知, 在目前大多数工作所采用的z/z评价方法下, 9种基准方法在ModelNet40数据集上取得了88.5%−92.2%的准确率. 然而一旦对测试集进行SO(3)增强, 即采用z/SO(3)评价方法, 我们发现, 准确率发生了断崖式下降. 因此, 如果训练阶段只采用沿z轴旋转增强的训练集, 前8种基准方法的旋转鲁棒性很差, 对于不同姿态下的三维物体泛化性能不足. 即使基于具有旋转等不变性的球形卷积, Spherical CNN基准方法也暴露出自身的缺点, 无法适应SO(3)增强的测试集, 分类准确率下降了12个百分点. 然而, 我们可以看到, 我们提出的算法(如表 2最后一行所示), 在z/SO(3)评价方法下依然保持87.1%的分类准确率, 这从实验层面证明了我们的方法具有严格旋转不变性. 不仅如此, 我们的方法在z/SO(3)评价方法下取得了最高准确率, 与其他基准方法相比最少提升10.2个百分点.
| 表 2 在ModelNet40点云分类数据集上, 各算法在3种评估方法下的分类准确率(%) |
继续观察表 2可知, 在SO(3)/SO(3)评价方法下, 若训练阶段也加入更加全面的SO(3)增强, 9种基准方法的旋转鲁棒性得到明显的提升, 但是与z/z评价方法相比基准方法的分类准确率平均下降7.1个百分点, 即基准方法虽然提升了对于旋转变换的鲁棒性, 但是牺牲了一部分的分类准确性. 导致这一现象可能的原因是: 由于模型的输入空间大大增加, 模型变得更难以收敛. 而我们可以看到, 由于我们的方法具有严格旋转不变性, 我们在SO(3)/SO(3)评价方法下依然保持87.1%的最高准确率, 与其他基准方法相比平均提升4个百分点.
3.1.3 内部组件分析在严格旋转不变性模块(RRI)中, K是唯一的超参数, 控制着图G的连通性. 因此, 我们探究在RRI中不同超参数K的设定下算法的性能表现. 如表 3所示, 实验结果表明, 我们的ClusterNet体系结构可以适应K的不同值. 例如, 当K=40时, 存在接近25%的点云不满足强连通条件, 但仍可达到有竞争力的分类准确率; 当K逐渐增加到70以上时, 模型的效果开始保持稳定.
| 表 3 在RRI中, 不同超参数K的设定下算法的性能表现 |
3.2 点云部位语义分割任务的实验
在上一节中, 我们介绍了点云分类任务下的实验结果. 接下来, 本节将详细介绍我们的方法与其他先进方法在点云部位分割任务上的综合性能. 同样地, 我们将介绍实验的具体设置, 比较本文提出的方法与其他基准方法在旋转鲁棒性上的性能差异; 并对部位语义分割结果进行可视化展示, 定性地考察模型在部位语义分割任务中的性能.
3.2.1 实验设置(1) 数据集介绍
在点云部位语义分割任务的实验中, 我们采用了被广泛使用的ShapeNetParts数据集[27]作为基准数据集. 如表 4所示, ShapeNetParts数据集包含16种物体类别, 总共16 881个三维点云数据, 其中, 12 137个点云作为训练集, 1 870个点云用于验证集, 而剩下的2 874个点云作为测试集. ShapeNetParts数据集中的三维点云总共标注了50种不同的部位, 例如飞机的机翼、杯子的把手等等, 其中每个点云至少标注了2种部位, 最多标注了5种部位. 除此之外, 数据集中的每个三维点云包含2 048个点, 即数据大小为2048×3.
| 表 4 ShapeNetParts部位语义分割数据集 |
(2) 评价指标与方法
我们采用平均交并比(mIOU)作为部位语义分割的评价指标, 并设计了4种评价方法.
1) None/None: 训练集与测试集均不采用任何旋转变换上的增强处理. 该评价方法为目前大多数算法在点云部位分割下的评价方法, 为了观察旋转变换对模型的影响, 我们将其列入实验中作为比较的对象.
2) None/SO(3): 训练集不采用旋转增强, 但是在测试阶段采用SO(3)增强后的测试集. 该评价方法用来测试现有的算法在常规训练方法下, 对于任意旋转变换的鲁棒性.
3) z/SO(3): 在训练阶段, 对训练集沿z轴旋转增强; 在测试阶段, 采用SO(3)增强后的测试集. 由于部分方法只在训练阶段采用z轴旋转增强, 我们将其列入实验之中来分析其旋转鲁棒性.
4) SO(3)/SO(3): 在训练阶段, 采用SO(3)增强后的训练集; 同样地, 在测试阶段, 也采用SO(3)增强后的测试集. 为了保证比较的公平性, 我们在模型训练阶段也使用SO(3)旋转增强方法, 在此基础上测试模型的效果.
3.2.2 外部对比实验为了验证层次聚类神经网络在三维点云部位分割任务中的优势, 我们通过上一节中介绍的4种评估方法来比较我们的模型与现有的先进方法在旋转鲁棒性上的性能.
(1) 基准方法
在对比实验中, 我们选取了6种先进方法作为基准方法, 其中既有不具有旋转鲁棒性的神经网络模型, 又包括结合了严格旋转不变性模块RRI的网络结构, 均为该任务下最先进的算法. 具体包括PointNet[6], PointNet (w/STN)[6], PointNet++[16], DGCNN(w/STN)[9], RRI+PointNet, RRI+DGCNN.
(2) 对比实验结果及其分析
表 5展示了各算法在ShapeNetParts数据集上的平均交并比mIOU(%), 其中采用了上一节所介绍的4种评价方法.
| 表 5 在ShapeNetParts部位分割数据集上, 各算法在4种评价方法下的平均交并比mIOU(%) |
由表 5可知:
● 在目前大多数工作所采用的None/None评价方法下, 前4种基准方法在ShapeNetParts数据集上取得了81.1%−84.7%的平均交并比(mIOU).
● 然而一旦对测试集进行SO(3)增强, 即采用None/SO(3)评价方法, mIOU均发生了断崖式下降. 这说明不具有旋转不变性的基准方法无法适应不同姿态下的三维物体, 其泛化能力很差.
● 即使在训练阶段加入z轴旋转增强, 即采用z/SO(3)评价方法, 我们会发现, 依然无法改变mIOU的断崖式下降. 这说明对训练集进行z轴旋转增强, 对于提升模型的旋转鲁棒性收效甚微.
● 而如果在训练阶段采用SO(3)增强的训练集, 即采用SO(3)/SO(3)评价方法, 基准方法PointNet, PointNet(w/STN)和DGCNN(w/STN)的mIOU依然分别下降了4.8, 4.0和6.7个百分点. 这从实验层面说明: 基于数据集旋转增强的方法只能在一定程度上缓解旋转灾难, 而无法彻底解决这一问题, 其旋转鲁棒性无法得到保证.
基于本文提出的严格旋转不变性模块RRI、基准方法RRI+PointNet与RRI+DGCNN在4种评价方法下均保持了相同的mIOU, 这从实验层面证明了本文提出的点云表达有良好的兼容性, 能够十分有效地提升模型的旋转鲁棒性, 使得原本旋转鲁棒性较差的算法具有严格旋转不变性. 此外, 我们提出的算法RRI+CluterNet不仅具有旋转不变性, 而且在None/SO(3), z/SO(3), SO(3)/SO(3)这3种基准方法下都取得了最好的表现.
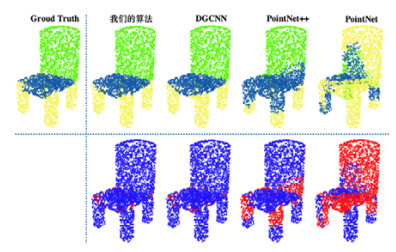
3.2.3 可视化结果分析如图 13−图 15所示, 我们分别展示了在SO(3)/SO(3)评价方法下, 我们的方法与其他3种基准方法对于吉他、椅子、笔记本电脑3种不同点云的部位语义分割结果. 图 13中第1行展示了点云部位语义分割的结果, 其中, Groud Truth为标准答案, 展示了每个点的真实的部位类别; 图中第2行展示了三维点云中部位类别预测正确的点(用蓝色表示)以及预测错误的点(用红色表示).

|
图 13 在SO(3)/SO(3)评估方法下, 各算法对吉他所对应的点云进行部位分割的可视化结果 |
|
图 14 在SO(3)/SO(3)评估方法下, 各算法对椅子所对应的点云进行部位分割的可视化结果 |

|
图 15 在SO(3)/SO(3)评估方法下, 各算法对笔记本电脑所对应的点云进行部位分割的可视化结果 |
观察图 13−图 15, 我们可以进行定性的分析: 我们提出的算法在3个点云上均取得了部位语义分割的最佳性能; 其他3种基准方法即使在训练阶段采用SO(3)增强的训练集, 即采用SO(3)/SO(3)评价方法, 它们的表现依然十分欠佳. 例如, PointNet++算法对吉他点云进行部位分割时, 明显缺失了吉他的颈部; PointNet算法对椅子点云进行部位分割时, 出现了大面积的预测错误, 椅背缺失严重; DGCNN算法对笔记本电脑点云进行部位分割时, 显示器面与键盘面的交界处发生了较多的误分类.
3.3 点云场景语义分割任务的实验本节将详细介绍我们的方法与其他先进方法在点云场景语义分割任务上的综合性能, 包括实验设置、外部对比实验以及可视化结果分析.
3.3.1 实验设置(1) 数据集介绍
在点云场景语义分割任务的实验中, 我们采用了被广泛使用的斯坦福大规模三维室内空间数据集S3DIS[28]作为基准数据集. 由表 6、表 7可知, S3DIS数据集包含6种不同类型的室内场景, 总共272个室内房间, 得到了带有语义标注的23 585个三维点云数据, 其中, 点云中的每个点可以被标注为13种不同的语义类别, 例如椅子、地面、墙壁等等. 每个三维点云的大小为4096×9.
| 表 6 S3DIS场景语义分割数据集 |
| 表 7 S3DIS数据集中6个场景的详细情况 |
(2) 评价指标与方法
由表 7可知, S3DIS数据集包含6种不同类型的室内场景, 每个场景下均采样得到了不同数目的三维点云. 为了综合评价模型的性能, 我们按照Charles R. Qi等人[6]采用的6-fold交叉验证的策略, 根据场景类型将整个S3DIS数据集分为6个部分, 按照第i个模型Modeli采用除场景i之外的全体场景作为训练集、剩下的场景i作为测试集的方法, 分别训练6个模型, 并依次计算各模型的平均交并比mIOU(%)以及平均分类准确率mAC(%), 然后对6个模型的平均交并比与平均分类准确率进行平均, 从而得到6-fold交叉验证策略下的总体平均交并比mIOU与总体平均分类准确率mAC, 我们将其作为本节实验的评价指标.
为了更全面地评估模型在点云语义分割任务中的综合性能, 我们基于总体平均交并比mIOU与总体平均分类准确率mAC, 采用了None/None, None/SO(3), SO(3)/SO(3)这3种评价方法.
3.3.2 外部对比实验(1) 基准方法
在对比实验中, 我们选取了5种先进方法作为基准方法, 包括PointNet[6], PointNet++[16], DGCNN[9], RRI+ PointNet, RRI+DGCNN.
(2) 对比实验结果及其分析
表 8展示了各算法在S3DIS数据集上关于场景语义分割的总体平均交并比mIOU(%)和总体平均分类准确率mAC(%), 其中采用了上节介绍的3种评价方法. 由表 8可知, 实验结果与点云部位语义分割任务保持一致, 再一次有力地验证了RRI模块具有旋转不变性, 我们提出的算法RRI+CluterNet可以取得最佳的综合性能.
| 表 8 在S3DIS场景语义分割数据集上, 各算法在3种评价方法下的总体平均交并比mIOU (%)以及总体平均分类准确率mAC (%) |
3.3.3 可视化结果分析
如图 16所示, 根据可视化结果, 我们可以进行定性分析: 我们的算法在场景语义分割上具有非常良好的性能, 能够十分有效地对点云场景进行语义层面上的理解.

|
图 16 我们提出的算法RRI+ClusterNet在S3DIS数据集上进行场景语义分割的可视化结果 |
4 未来展望
本文虽然在三维点云分析问题上取得了一些成果, 但依然存在不少改进空间及进一步拓展的研究方向.
(1) 目前, 计算机三维视觉领域中, 基于三维点云的模型往往需要稠密点云(点云中包含的点的数目较大)作为输入, 然而在无人驾驶等实际应用中, 往往获取到的是十分稀疏的点云, 这种苛刻的条件对于目前绝大多数先进方法而言, 其识别精度都会不可避免地发生大幅下降. 因此, 对于点云疏密程度具有鲁棒性的方法将会是未来的主流. 在后续的工作中, 我希望将点云密度鲁棒性作为进一步探索的研究方向.
(2) 在本文的实验部分, 我们进行了点云识别、点云部位语义分割以及点云场景语义分割三大任务的实验. 但是在无人驾驶等实际应用中, 三维物体检测也是一种非常重要的任务需求, 它对避障、紧急制动等动作的规划与执行具有深刻的意义. 因此在未来的工作中, 我们计划将现有的ClusterNet网络结构拓展为可应用于物体检测的版本, 并且增加三维物体检测任务的对比实验与定性分析.
(3) 由于三维点云其实可以看作一种没有边集的特殊图结构, 因此本文提出的ClusterNet其实可以很自然地应用于图数据. 换言之, 我们可以将ClusterNet拓展为图神经网络, 用来学习图数据中的各个节点的嵌入表达. 在后续的工作中, 我希望将我们的工作从计算机三维视觉领域迁移到几何深度学习领域, 在更加通用的非欧式数据中学习数据所蕴含的关联信息.
| [1] |
Goodfellow IJ, Shlens J, Szegedy C. Explaining and harnessing adversarial examples. arXiv: 1412.6572, 2014.
|
| [2] |
Kurakin A, Goodfellow I, Bengio S. Adversarial machine learning at scale. arXiv: 1611.01236, 2016.
|
| [3] |
Tramèr F, Kurakin A, Papernot N, Goodfellow I, Boneh D, McDaniel P. Ensemble adversarial training: Attacks and defenses. arXiv: 1705.07204, 2017.
|
| [4] |
Zhou H, Chen KJ, Zhang WM, Fang H, Zhou WB, Yu NH. DUP-net: Denoiser and upsampler network for 3D adversarial point clouds defense. In: Proc. of the IEEE Int'l Conf. on Computer Vision. 2019. 1961−1970.
|
| [5] |
Zhang Q, Yang JC, Fang RY, Ni BB, Liu JX, Tian Q. Adversarial attack and defense on point sets. arXiv: 1902.10899, 2019.
|
| [6] |
Qi CR, Su H, Mo KC, Guibas LJ. PointNet: Deep learning on point sets for 3D classification and segmentation. In: Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition. 2017. 652−660.
|
| [7] |
Klokov R, Lempitsky V. Escape from cells: Deep Kd-networks for the recognition of 3D point cloud models. In: Proc. of the IEEE Int'l Conf. on Computer Vision. 2017. 863−872.
|
| [8] |
Riegler G, Ulusoy AO, Geiger A. OctNet: Learning deep 3D representations at high resolutions. In: Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition. 2017. 3577−3586.
|
| [9] |
Wang Y, Sun YB, Liu ZW, Sarma SE, Bronstein MM, Solomon JM. Dynamic graph CNN for learning on point clouds. ACM Trans. on Graphics (TOG), 2019, 38(5): 1-12.
|
| [10] |
Ward JH. Hierarchical grouping to optimize an objective function. Journal of the American Statistical Association, 1963, 58(301): 236-244.
[doi:10.1080/01621459.1963.10500845] |
| [11] |
Murtagh F, Legendre P. Ward's hierarchical agglomerative clustering method: Which algorithms implement ward's criterion?. JJournal of Classification, 2014, 31(2): 274-295.
|
| [12] |
Müllner D. Modern hierarchical, agglomerative clustering algorithms. arXiv: 1109.2378, 2011.
|
| [13] |
Lance GN, Williams WT. A general theory of classificatory sorting strategies: 1. hierarchical systems. The Computer Journal, 1967, 9(4): 373-380.
|
| [14] |
Galler BA, Fisher MJ. An improved equivalence algorithm. Communications of the ACM, 1964, 7(5): 301-303.
[doi:10.1145/364099.364331] |
| [15] |
Hopcroft JE, Ullman JD. Set merging algorithms. SIAM Journal on Computing, 1973, 2(4): 294-303.
[doi:10.1137/0202024] |
| [16] |
Qi CR, Yi L, Su H, Guibas LJ. PointNet++: Deep hierarchical feature learning on point sets in a metric space. In: Proc. of the Advances in Neural Information Processing Systems. 2017. 5099−5108.
|
| [17] |
Krizhevsky A, Sutskever I, Hinton GE. ImageNet classification with deep convolutional neural networks. In: Proc. of the Advances in Neural Information Processing Systems. 2012. 1106−1114.
|
| [18] |
Hinton GE, Srivastava N, Krizhevsky A, Sutskever I, Salakhutdinov RR. Improving neural networks by preventing co-adaptation of feature detectors. arXiv: 1207.0580, 2012.
|
| [19] |
Srivastava N, Hinton GE, Krizhevsky A, Sutskever I, Salakhutdinov R. Dropout: A simple way to prevent neural networks from overfitting. The Journal of Machine Learning Research, 2014, 15(1): 1929-1958.
|
| [20] |
Kingma DP, Ba J. Adam: A method for stochastic optimization. arXiv: 1412.6980v9, 2017.
|
| [21] |
Wu ZR, Song S, Khosla A, Yu F, Zhang LG, Tang XO, Xiao JX. 3D ShapeNets: A deep representation for volumetric shapes. In: Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition. 2015. 1912−1920.
|
| [22] |
González Á. Measurement of areas on a sphere using Fibonacci and latitude—Longitude lattices. Mathematical Geosciences, 2010, 42(1): 49-64.
[doi:10.1007/s11004-009-9257-x] |
| [23] |
Qi CR, Su H, Niessner M, Dai A, Yan MY, Guibas LJ. Volumetric and multi-view cnns for object classification on 3D data. In: Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition. 2016. 5648−5656.
|
| [24] |
Su H, Maji S, Kalogerakis E, Learned-Miller E. Multi-view convolutional neural networks for 3D shape recognition. In: Proc. of the IEEE Int'l Conf. on Computer Vision. 2015. 945−953.
|
| [25] |
Esteves C, Allen-blanchette C, Makadia A, Daniilidis K. Learning SO(3) equivariant representations with spherical CNNs. In: Proc. of the European Conf. on Computer Vision. 2018. 52−68.
|
| [26] |
Jaderberg M, Simonyan K, Zisserman A, Kavukcuoglu K. Spatial transformer networks. In: Advances in Neural Information Processing Systems. 2015.
|
| [27] |
Yi L, Kim VG, Ceylan D, Shen IC, Yan MY, Su H, Lu CW, Huang QX, Sheffer A, Guibas L. A scalable active framework for region annotation in 3D shape collections. ACM Trans. on Graphics (ToG), 2016, 35(6): 1-12.
|
| [28] |
Armeni I, Sener O, Zamir AR, Jiang H, Brilakis I, Fischer M, Savarese S. 3D semantic parsing of large-scale indoor spaces. In: Proc. of the IEEE Int'l Conf. on Computer Vision and Pattern Recognition. 2016. 1534−1543.
|
 2022, Vol. 33
2022, Vol. 33


