2. 武汉大学 数学与统计学院, 湖北 武汉 430072
2. School of Mathematics and Statistics, Wuhan University, Wuhan 430072, China
区块链技术自诞生以来, 就以其开放、去中心化、可公开验证等特性备受欢迎. 然而, 随着参与人数的激增, 区块链系统中的一些问题逐渐暴露出来. 因其无需许可和去中心化的特性, 比特币系统平均挖矿时间为每个块10分钟, 且每秒最多只能处理7笔交易. 这样的性能显然无法满足比特币市场上日益增长的交易需求.此外, 由于比特币挖矿过程与交易的金额无关, 这意味着在其他相关因素相同的情况下, 不同交易金额的交易所要支付的交易费用是相同的. 显然, 这种收费机制对于小额交易来说十分不经济. 为了解决上述问题, 支付通道网络(payment channel network, PCN)应运而生. 不久后, 闪电网络(lightning network, LN)[1]作为一种支付通道网络, 被部署在比特币系统上.
由于主流加密货币(例如比特币和以太坊)的去中心化本质极大地阻碍了其交易吞吐量, 支付通道网络成为解决区块链可扩展性问题和高昂的交易费用问题的有效途径. 支付通道可被理解为是一个交易双方的账本, 由两位用户自行建立和维护. 交易双方无需向区块链报告每一笔具体的交易, 只需将开通和关闭支付通道的事务提交到区块链上, 以保障链下交易安全, 使得交易双方能够取回自己的合法资金. 开通支付通道时, 两位用户需在区块链上进行存款操作, 锁定其抵押资金作为链下账本的初始资金. 在之后的交易中, 双方通过链下消息发布账本余额变化, 进行转账. 当双方达成协议, 决定关闭该交易通道时, 账本中记录最新的通道余额分配状态会被报告给区块链, 双方进而可以取回其应得的合法资金. 在多个支付通道组成的支付通道网络中, 用户不仅能和与其直接相连的用户进行交易, 还能和与其间接相连的用户进行交易, 这样的过程涉及多个用户参与的多跳交易. 总而言之, 由于链下的支付通道网络可以进行大量实时的交易, 极大地提高了交易的吞吐量; 同时, 支付通道网络中的交易费用与区块链上的交易费用相比微不足道.
闪电网络作为基于比特币系统的支付通道网络, 是目前被最广泛使用和研究的支付通道网络. 除了上文所述的运行机制外, 闪电网络采用特定的智能合约来确保其运作. 例如: RSMC (revocable sequence maturity contract)机制确保资金只能经过交易双方的同意或预先拟定的退款程序退还, 并且只接收链下账本中余额分配的最新状态; HTLC (hashed time lock contract)机制通过引入nLockTime概念来处理多跳交易, 以确保交易的原子性. 然而, 闪电网络的蓬勃发展也逐渐暴露出一些问题. 例如, 人们会担心闪电网络中是否会出现超级中心节点, 破坏其去中心化的属性. 此外, 如何在闪电网络中寻找最有效且经济的支付路由, 也是一个重要问题. 这些问题都与闪电网络静态和动态的拓扑特征密切相关.
虽然闪电网络投入使用距今不到3年, 但学术界已有许多相关研究[2−7]. Martinazzi等人[3]研究了闪电网络的拓扑特征演化及其效率和同步性, 并涉及了安全问题. 文献[4]量化了闪电网络对基于拓扑结构的攻击的抵抗能力. 然而, 这些研究都有很强的时间局限性. 文献[2−4]均使用了2018年2月−2019年1月约1年时间的闪电网络通道数据, 在这段时间内, 闪电网络仍处于刚起步的快速发展阶段, 数据缺乏必要的时效性. 在这一阶段, 人们往往出于好奇而试探性地使用闪电网络, 其相关的数据分析十分有限, 不足以反映闪电网络趋于稳定发展阶段后的特性. 除上述方面外, 闪电网络中的路由问题也具有重要的研究价值. Flare[5]是当前闪电网络的路由方法, 用以尽快找到支付路径. 一些研究者还提出了其他新颖的路由方法. 例如, 文献[6]中提出的多径路由支付方案, 大大降低了交易的费用. 此外, 还有一些关于闪电网络中交易仿真的研究, Béres等人[7]为闪电网络设计了一个用于分析不同节点的路由成本和潜在收益的流量模拟器.
本文旨在全面、系统地了解闪电网络, 以期解决闪电网络中存在的一些问题. 因此, 本文全面分析了闪电网络的拓扑特征、发展趋势及其收费机制. 基于截至2020年7月更新的通道数据, 对闪电网络的静态和动态特征及其收费策略进行了评估. 本文的研究工作分为3部分.
● 第1部分关注闪电网络的静态拓扑结构. 通过图分析的方法, 对闪电网络的静态拓扑特征给出全面、细致的解释. 具体来讲, 对闪电网络的重要属性、典型特征的分布进行了分析, 并使用聚类方法探索闪电网络中节点之间的共性;
● 第2部分关注闪电网络的动态拓扑变化. 深入研究了闪电网络规模、节点和通道特征的演化趋势, 进而了解闪电网络的发展趋势. 由于闪电网络是在2016年[1]设计的, 2018年1月被部署到比特币主网上使用, 其应用时间十分有限. 在此背景下, 与以往针对闪电网络展开的研究相比, 本文更关注闪电网络处于稳定发展阶段的网络特征和发展特性, 结果具有较高的时效性, 且丰富的通道数据也加强了结论和预测的可靠性;
● 第3部分关于闪电网络的收费机制. 在闪电网络中进行模拟交易(一种路由策略以交易费用最小化为目标, 另一种路由策略以路径长度最小化为目标), 以获取不同交易金额下的交易费用, 并对链上的交易费用进行合理估计, 进而比较链上和链下交易费用的差异.
本文的主要贡献如下:
● 基于大量具有高时效性的数据, 对闪电网络的静态和动态拓扑特征进行系统分析. 根据闪电网络的动态拓扑特征, 分析闪电网络的发展趋势;
● 对闪电网络中的节点进行聚类分析, 最终将节点划分为4类, 并对聚类结果给出合理的解释和可能的应用情境;
● 深入理解闪电网络的收费策略. 通过对链上和链下交易费用的比较, 对闪电网络的收费机制进行综合分析. 为了得到链下交易费用, 采取交易费用最小化和路径长度最小化两种路由策略进行交易路由的模拟.
1 背景 1.1 支付通道网络区块链因其开放、去中心化、可公开验证的特性, 被看作是一种具有颠覆性的创新技术. 然而, 比特币网络的交易广播机制导致其交易吞吐量非常低, 每秒最多只能处理7笔交易, 而其他集中支付方法(例如MasterCard和Visa)在高峰时期的交易速度高达每秒4万笔. 此外, 比特币链上交易费用对于小额交易来说十分昂贵. 用户无疑希望支付较低的交易费用来完成交易. 所以在比特币交易中, 特别是在小额、高频的交易中, 用户一直都在寻求一种更经济的交易方式. 因此, 研究人员提出了一些方法[7−10], 用以解决上述区块链可扩展性问题, 其中一个很有应用前景的方案是支付通道网络.
支付通道网络作为一种基于区块链的、无需第三方可信机构验证的机制, 使得用户在比特币链下完成交易, 为区块链可扩展性问题和交易费用高昂等问题提供了一个较为理想的解决方案. 支付通道使得链上缓慢、昂贵的交易可以在链下快速、低廉地进行. 交易双方只需在开通和关闭支付通道时与区块链进行交互, 而其他交易可以通过支付通道在链下进行. 交易的安全性通过一些特定的协议(例如RSMC[1])来保证, 以防止由于一方单方面放弃交易而损害另一方利益的情况发生. 随着参与者和支付通道数的增加, 形成了由节点(参与者)和边(支付通道)组成的网络, 即支付通道网络.
应用支付通道网络进行交易的过程可分为以下3个阶段.
(1) 开通支付通道. 开通支付通道的事务是在链上进行的. 在这一阶段, 双方合作开通通道, 并在其中锁定自己的抵押资金. 资金被交付到一个2-of-2多重签名地址, 只有在双方签名后才能退还抵押资金或取回交易后的资金;
(2) 进行链下交易. 这一阶段是在链下进行的, 交易双方在支付通道中交换他们的余额. 根据设置的不同, 这个支付通道可以是双向的, 也可以是单向的. 交易细节仅限于交易双方, 即在区块链链上不会有任何链下交易的痕迹. 多重签名机制可以在不公开广播的情况下保证交易的安全性. 双方可以进行多次交易, 并在每次余额分配发生变化时实时更新多重签名地址. 但是, 由于支付通道仍然使用统一签名锁定, 没有人能够取出超出其应得金额的资金, 通道中的余额总额也不会改变. 当双方达成协议不再进行余额转移时, 就进入了下一阶段;
(3) 关闭支付通道. 关闭支付通道的事务是在链上进行的. 在双方对支付通道中的最终余额分配达成共识后, 他们交换彼此的签名, 通过有效的2-of-2多重签名在关闭交易中取回各自账户上的资金. 至此, 支付通道得以成功关闭.
1.2 闪电网络闪电网络是目前最著名的支付通道网络, 它于2016年[1]被提出, 并于2018年1月在比特币主网上发布, 随后吸引了大批参与者加入. 闪电网络作为第一个比特币支付通道网络的应用, 实现了比特币链下交易的总体框架. 除上文中介绍的工作原理外, 本节主要介绍闪电网络中维持交易原子性的协议以及闪电网络的收费机制.
在闪电网络中, 两个不直接相连的节点可以通过中间节点进行多跳交易支付. 例如, Alice和Bob、Bob和Carol分别有直接相连的支付通道, Alice和Carol之间无直接相连的支付通道, 但Alice和Carol之间的交易可以通过Alice先转账给Bob, Bob再转账给Carol来实现. 在多跳交易中, 需特别关注交易的原子性问题. 闪电网络的HTLC协议[1]使得多跳交易得以维持原子性. 多跳交易的原子性是指, 当交易的每一跳支付都顺利完成后, 交易所涉及到的所有通道的余额分配都会更新. 然而一旦有一笔支付没有完成, 则该次交易就会被认定为失败, 所有相关支付通道的余额分配均不会发生更改. 交易双方可以在双向的支付通道中安全地进行交易, 但是跨越多个通道进行安全的资金转移需要额外的设计. 闪电网络提出HTLC来保障交易的安全性和原子性. 在闪电网络中, 每一跳支付, 中间节点用户在限制时间内, 根据交易对象提供的有关原像R的信息来完成哈希值的计算, 进而使交易能够传递到下一跳. 关于原像R和哈希值的计算, 继承了区块链工作机制的特性, 从而保证了交易的安全性. 在规定的时间范围内, 交易资金会保持锁定在通道中. 一旦交易的某一跳停止或超时, 本次交易将被取消, 所有通道的状态将恢复到此次交易之前的状态.
关于闪电网络的收费机制, 闪电网络的使用涉及开通和关闭支付通道、进行链下交易等过程. 由于开通和关闭支付通道的过程是在链上进行的, 闪电网络内的支付交易是在链下进行的, 这里, 我们对链上和链下两类交易费用进行了解释.
(1) 链上交易费用. 如第1.1节所述, 开通支付通道和关闭支付通道的交易都是在链上完成的, 这意味着这些交易的费用是严格按照区块链的工作机制产生的. 当双方对一个链上交易达成共识时, 他们会将本次交易发布到网络中, 并等待网络中的矿工进行计算来验证交易的正确性. 当交易被打包进区块, 且该区块经过验证被成功添加到主链上后, 双方才会认可本次交易有效. 也就是说, 区块链运行的关键是让网络中所有节点对区块的内容达成一致, 然后将其添加到主链上. 这个过程中, 区块实际上充当了交易的记录簿. 因为验证区块时的计算消耗了电力、计算能力及众多其他资源, 矿工需要金钱奖励去驱动他们进行验证. 因此, 交易双方对交易被验证的需求与矿工通过采矿工作获取利润的意愿进行匹配, 构建了在区块链上进行转移资金的交易方式. 基于以上背景可知: 支付给矿工的交易费用和交易的实际金额无关, 而是与交易广播时区块验证的计算难度有关, 也即与比特币系统在交易时的状况密切相关. 因此, 当交易金额较大时, 单位交易金额对应的交易费用是经济实惠的; 否则, 单位交易金额的交易费用不容小觑;
(2) 链下交易费用. 前文中详细说明了在闪电网络中如何通过中间节点进行多跳交易. 在多跳交易中, 为激励中间节点辅助转移资金, 支付路由成功后, 中间节点可以得到一些奖励, 如一定数额的资金.这就是链下交易费用的来源. 在闪电网络中, 中间节点具有自己独特的收费策略, 它们可以自行设置两种类型的费用, 即基础费用(base fee)和费率(fee rate). 基础费用是指当有交易经过该中间节点时便会收取的固定费用. 费率是一个比率, 代表每转移1 sat需要收取的费用. 因此, 支付给中间节点的交易费用可以表示为公式(1), 其中, F代表总的交易费用, Fbase代表基础费用, r代表费率, a代表流经中间节点的交易金额:
| $ F=F_{base}+r×a$ | (1) |
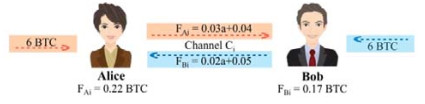
在闪电网络中, 每条支付通道(视为无向边)会有两个不同的收费函数, 分别由该边所连的两个节点预先设定. 收费函数的自变量是交易金额, 因变量是交易费用. 这里对收费模型进行简化, 将自变量设定为交易金额而不是转账金额(注: 转账金额是流经中间节点的资金总量, 是交易金额与交易费用之和). 这两个收费函数一般是不同的, 是由两个收费方独立设置的. 由于只有当资金流出一个中间节点时它才会收取费用, 因此, 当资金沿支付通道某一方向流动时, 有且仅有一个收费函数会生效, 即资金流出节点的收费函数. 本文中, 我们将收费函数表示为包含两个参数(截距和斜率)的线性函数. 截距的实际意义是基础费用, 斜率的实际意义是费率. 利用下面的场景来解释收费的具体过程. 如图 1所示: 对于Alice和Bob之间的通道Ci, Alice将其收费函数设置为
|
图 1 付款给闪电网络中间节点 |
2 数据采集与研究方法
自2018年1月闪电网络在比特币主网发布以来, 开通支付通道和关闭支付通道的事务数据都被提交到区块链上, 这些数据对公众是开放的. 本文在闪电网络数据统计网站[8]上收集了自其2018年1月12日发布截止到2020年7月22日的这些数据, 并进一步加以整理分析. 具体来讲, 本文收集了闪电网络支付通道的全面信息, 包括节点、通道余额、开通和关闭通道的状态、节点的收费策略等. 通过这些数据, 可以分析闪电网络当前的静态拓扑特征、历史特征及其发展趋势.
本文把闪电网络看作是一个无向带权多重图G=(V, E)(多重图指的是在两个节点之间存在多条边的图, 需要指出闪电网络中的确存在两个节点之间有多条通道的情况). 其中, V是节点的集合, E是边(即支付通道)的集合. 节点vi和节点vj之间的通道表示为eij. eij的权值为通道的余额. 此外, 视情况为节点和边赋予其他相关属性, 如节点的收费策略、通道的开闭时间等. 基于收集到的闪电网络数据构建网络图, 从多方面深入研究闪电网络的特征.
本文捕获了2020年7月22日闪电网络的快照, 用以分析其静态拓扑结构. 基于捕获的快照, 本文构建了一个共包含7 647个节点、38 659条边的无向多重图. 选取一些常用于衡量网络特征的属性进行计算, 并做出有关解释. 将闪电网络与其他几种典型网络进行对比, 观察其共性与差异. 同时, 对闪电网络的连通分量及典型特征的分布进行分析. 此外, 对闪电网络中节点进行聚类, 深入分析节点特征. 为此, 本文第3节详细介绍了闪电网络的静态拓扑结构.
为了在时间维度上了解闪电网络, 以研究其发展趋势, 本文自2018年2月−2020年7月在每月的1日对闪电网络摄取一张快照, 共计获得30张快照. 为每张快照构建网络图, 对关乎闪电网络规模和特征的重要指标进行计算, 得到其时间序列上的演化过程, 进而得以了解闪电网络的发展趋势. 此外, 对通道的存在时间及其关闭方式进行研究, 从时间维度上细致地了解闪电网络. 上述内容的详细分析见本文第4节.
为了进一步明晰闪电网络的收费策略, 本文还对链上和链下的交易费用进行了对比. 在衡量链下交易费用时, 本文使用了两种路由策略, 即费用最小化路由策略和路径长度最小化路由策略. 在这一部分中, 将闪电网络视为一个有向图, 将一个支付通道视为两条有向边, 利用Dijkstra最短路径算法构造单路径支付路由, 并估算每笔交易的花费. 具体来讲, 本实验随机选择收款人和在其通道中有足够余额的付款人, 计算两种路由策略下不同交易金额情况下的交易费用和路径长度. 每种情况共进行500次支付路由模拟, 计算平均交易费用、平均路径长度和交易成功率. 关于收费特征的详细分析见本文第5节.
3 闪电网络静态拓扑结构 3.1 基本属性本文基于2020年7月22日捕获到的闪电网络快照, 构建一个共包含7 647个节点、38 659条边的网络.闪电网络拓扑结构的基本属性见表 1. 网络中的总余额是1 003.5 BTC. 节点平均度为10.11. 闪电网络度的同配性为−0.25. 度的同配性是指, 从网络结构的角度考虑节点之间相互连接的可能性. 闪电网络的度同配性为负数, 说明网络中的低度节点更倾向于与高度节点相连, 这意味着闪电网络中可能存在一些较为中心的高度节点.
| 表 1 闪电网络基本属性 |
图的密度是用来衡量网络稀疏性的, 它被定义为公式(2), 即实际存在边数与可容纳边数上限的比值:
| $ D = \frac{{2|E|}}{{|V||V - 1|}} $ | (2) |
闪电网络的网络密度是0.001 3, 说明闪电网络是一个稀疏的网络.
网络传递性表示图中所有现存三角形与潜在三角形的比, 定义为公式(3):
| $ T = \frac{{3 \times number{\text{ }}of{\text{ }}trangles}}{{number{\text{ }}of{\text{ }}paths{\text{ }}of{\text{ }}length{\text{ }}2}} $ | (3) |
闪电网络的传递性是0.063 7, 这进一步验证了其稀疏性.
局部聚类系数用以衡量一个节点的邻居节点之间的连接程度. 公式(4)定义了节点u的局部聚类系数:
| $ CC(u) = \frac{{2|{e_{vw}}|}}{{deg(u)(deg(u) - 1)}},{\text{ }}v,w \in N(u),{\text{ }}{e_{vw}} \in E $ | (4) |
其中, deg(u)是节点u的度数, N(u)代表节点u邻居节点的集合. 闪电网络的聚类系数较高, 它的平均局部聚类系数为0.206 8.
为了更好地了解闪电网络的特征, 本文将闪电网络的平均聚类系数、传递性和同配性与相同规模下的典型网络进行对比, 包括规则图、随机图、小世界网络和无标度网络.
规则图是指每个节点都有相同数量的邻居节点(即相同的度)的图. 在随机图中, 每两个节点连接的概率相同, 每条边是否连接相互独立. 小世界网络的特点是节点倾向于聚集且网络密度较高. 无标度网络的特点是绝大多数节点为低度节点, 仅有少部分节点为高度节点. 无标度网络的度分布服从幂律分布, 度为k的节点比例为P(k), 表示为P(k)~k−ɑ, 其中, ɑ的典型范围在2~3之间.
如表 2所示, 闪电网络的平均聚类系数与小世界网络的类似, 比其他网络的大得多. 然而, 闪电网络的网络传递性比小世界网络小得多. 这表明: 尽管闪电网络中的节点倾向于聚集, 但正如前面提到的, 它仍然是一个稀疏的网络. 由于规则图中每个节点的度相同, 则不考虑同配性. 其余4种网络均表现出负的同配性, 说明低度节点更倾向于与高度节点相连, 且闪电网络的这种倾向性比其他网络更加突出.
| 表 2 与同等规模典型网络的对比 |
3.2 连通分量
对于子图G′=(V′, E′), V′⊂V, E′⊂E, 如果任何一个节点u∈V′是V′中其他任何节点都可达的, 则被称作连通分量. 如表 3所示, 闪电网络由48个连通分量组成. 表中的通道平均存在时间指的是从通道开通到捕获快照时的时间间隔.
| 表 3 连通分量的一些特征 |
闪电网络的最大连通分量具有7 544个节点和38 601个通道, 它的网络直径是12, 平均最短路径长度为3.52. 两个节点之间的距离被定义为它们之间的最短路径, 网络直径是指网络中任意两个节点之间距离的最大值. 这个最大连通分量聚集了闪电网络中98.7%的节点, 在闪电网络中占据主要地位. 关于连通分量的分析表明, 闪电网络实际上是由一个大的中心团簇和一些松散的外围连接组成的.
如表 3所示, 其余47个连通分量均由少量节点组成. 关于仅包含2个或3个节点的连通分量, 对于它们存在的可能原因, 本文提供以下3种猜测.
● 首先, 一些交易双方或者小团体可能会通过闪电网络进行较为频繁的交易. 他们只与对方或者小团体中的其他人进行交易, 所以无需与其他各方相连;
● 其次, 可能存在一些想要尝试闪电网络这一新兴事物的用户, 会自己或与同伴开通一个或两个通道进行实验;
● 此外, 还有一些研究者或许想要进一步研究闪电网络特性并提出相关完善措施, 因此他们形成了小的团队并进行研究.
对于仅有的包含5个节点的连通分量, 其通道平均存在时间为672天, 远大于其他连通分量. 因此, 它的存在倾向于是上述第1种原因. 最大连通分量的通道平均余额远远超过其他连通分量, 这表明其中存在一些中心节点. 但其通道的平均存在时间比其他连通分量都低, 这是由于, 它是闪电网络中最活跃的部分, 有很多新开通的通道都加入了进来.
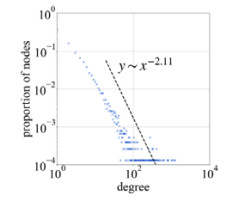
3.3 典型特征的分布图 2展示了闪电网络的度分布情况, 可以看出: 闪电网络中仅有少数高度节点, 大部分为低度节点. 这与先前提到过的无标度网络非常相似. 为了对此进一步加以验证, 采用文献[9]中介绍的方法, 使用极大似然估计来进行幂律拟合. 该度分布的幂律拟合ɑ值为2.11, 因此得到幂律函数为y~x−2.11, 度分布的拟合线如图 2中虚线所示. 此外, 本文使用Kolmogorov-Smirnov (KS)距离来定义真实数据与幂律拟合之间的差异. 通过最小化KS距离, 得到xmin值为19, 进行拟合优度检验后, 得到p值为0.90, 大于0.10, 因此接受幂律分布假设. 总的来说, 闪电网络度分布服从幂律分布, 表明闪电网络是一种无标度网络.
|
图 2 度分布 |
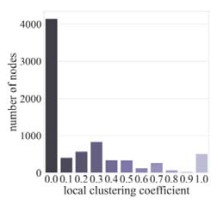
图 3展示了局部聚类系数的分布情况, 这表明闪电网络本质上是由一个居优势地位的中心群体和松散连接的外围所组成.
|
图 3 局部聚类系数分布 |
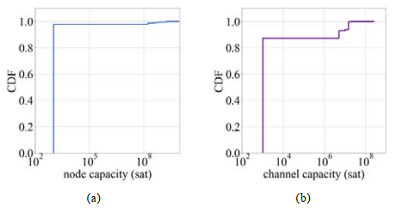
图 4展示了节点余额和通道余额的累积分布函数(cumulative distribution function, CDF). 从图中可以看出, 82.5%的节点和90.8%的通道余额不超过107 sat (=0.1BTC). 对于余额大于0.1 BTC的节点和通道, 我们称之为大型节点和大型通道. 由表 4可知, 17.5%的节点拥有闪电网络节点总余额的95.9%, 9.2%的通道拥有闪电网络通道总余额的59.1%, 这表明, 少数的节点和通道占据了大部分的闪电网络资源.
|
图 4 节点和通道余额分布 |
| 表 4 大型节点和通道 |
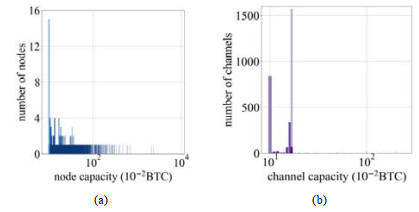
图 5展示了大型节点和大型通道余额的分布情况. 大型节点余额的分布集中在0.1~1.0 BTC, 大型通道余额的分布集中在0.1~0.2 BTC. 此外, 大型通道的平均存在时间为278天, 而全体通道的平均存在时间为341天. 这说明, 一些大型通道加入闪电网络的时间相对较晚.
|
图 5 大型节点和通道余额分布 |
3.4 节点聚类分析
为了进一步认识闪电网络中节点的特征和行为, 本文对节点进行了聚类分析. 选取并计算节点的一些属性进行聚类, 包括度、余额、聚类系数、度中心性(degree centrality)、接近中心性(closeness centrality)、中介中心性(betweenness centrality)、特征向量中心性(eigenvector centrality)、基础费用和费率.
网络中节点的重要性可以用节点的中心性来衡量. 度中心性、接近中心性、中介中心性和特征向量中心性是衡量节点中心性的4种主要方法. 度中心性是用节点的度来衡量其中心性. 节点u的接近中心性被定义为公式(5), 其中, d(v, u)是v和u之间的最短路径距离, n是可到达u的节点数. 接近中心性用来衡量节点与其他节点间的接近程度. 公式(6)定义了节点v的中介中心性, 其中, V是节点的集合, σ(s, t)是s和t之间所有的最短路径数, σ(s, t|v)是s和t之间所有经过v的最短路径数. 中介中心性是节点对网络控制程度的展现. 节点的特征向量中心性基于其邻居节点的中心性. 与得分高的节点相连, 比与得分低的节点相连对节点分数的贡献要大, 基于此概念, 为网络中的所有节点分配相对分数:
| $ C(u) = \frac{{n - 1}}{{\sum\limits_{v = 1}^{n - 1} {d(v,u)} }} $ | (5) |
| $ {c_B}(v) = \sum\limits_{s,t \in V} {\frac{{\sigma (s,t|v)}}{{\sigma (s,t)}}} $ | (6) |
本文使用无监督学习的K-Means聚类算法对闪电网络中节点进行聚类. 通过对聚类效果的评估发现: 当把闪电网络中的节点分为4类时, 聚类效果最好. 聚类结果见表 5. 第1类包含7 594个节点, 占据闪电网络节点数的99.3%. 该类节点余额较低. 它们的度非常低, 意味着少有邻居节点. 但是该类节点的聚类系数是这4类中最高的, 与此同时, 中心性却比其他都低, 说明它们在闪电网络中的重要性比较低. 此外, 第1类节点的费率比其他3类高很多, 该类中的一些节点可能是为了收取交易费用、赚取资金而建立通道. 第2类和第3类节点在闪电网络中较为重要, 共计包含52个节点, 它们的度、余额、聚类系数、中心性都很高. 显然, 它们就是网络中的中心节点. 与第2类节点相比, 第3类节点在网络中的重要性更高. 第2类节点的基础费用较低, 但费率较高. 第4类节点尤为特别, 因为仅包含一个节点. 进一步探索发现, 这个节点是“ACINQ”, 为闪电网络的主要研发公司之一. 从表中可以看出, 它的中心性很高, 是闪电网络中至关重要的节点. 它的度和余额是第3类节点的两倍多. 然而它的费率很低, 说明它并不是为了收取交易费而存在的.
| 表 5 节点聚类结果 |
4 闪电网络的发展趋势 4.1 闪电网络的演化
本文从2018年2月−2020年7月在每月第1天捕获闪电网络的快照, 进而获得了闪电网络一些特征的演化趋势.
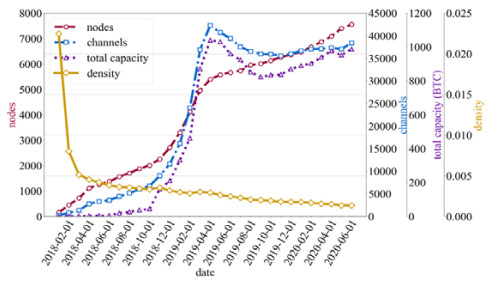
首先研究闪电网络规模随时间的变化情况. 如图 6所示, 闪电网络规模呈扩大态势. 节点数稳步增长, 在闪电网络发布初期增长相对较缓, 随后迎来半年多的快速增长时期, 之后便是缓慢增长阶段. 闪电网络通道数与网络总余额的演化趋势较为相似. 它们在2019年1月−5月之间增长非常迅速, 之后经历了一段时间的下降, 随后呈现逐渐增长的趋势. 闪电网络的网络密度在开始阶段急剧下降, 之后保持下降趋势.
|
图 6 闪电网络规模发展趋势 |
本文收集了相关资料, 以进一步分析闪电网络经历快速增长期和下降期的原因. 2019年年初, 一个匿名的比特币用户“hodlonaut”发起了“闪电火炬”活动[10], 吸引了全球近300名用户通过闪电网络转移比特币, 其中一些用户在比特币行业非常有名. “闪电火炬”活动使得人们对闪电网络这项技术的发展充满信心. 应用层发展迅速, 钱包数量呈指数型增长. 此外, 一些基础功能(例如瞭望塔[11]和多路径支付)被添加到闪电网络中.随着闪电网络得到更多的关注, 参与者数目显著增加. 然而在2019年5月−10月之间, 网络总余额下降了近27%. 闪电网络开发者Russel表示, 这个下降可能与比特币价格的上涨有关. 或许很多用户认为, 相比于将手中持有的比特币放在一个应用不多的地方, 趁着现有牛市套现更为实际. 值得一提的是, 从2019年11月开始, 闪电网络重新展现出上升态势, 这可能是由于技术或应用上有了新的突破[12].
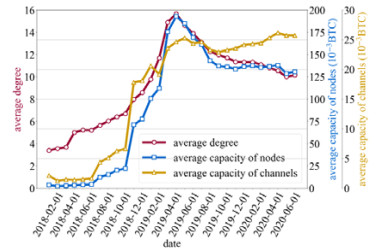
根据图 6所示的闪电网络规模演化趋势, 很容易理解图 7所示的节点和通道特征的演化趋势. 在演化趋势的后期, 由于通道数的增长程度低于节点数的增长程度, 节点平均度呈下降趋势. 节点和通道平均余额的演化趋势亦是如此.
|
图 7 节点和通道特征发展趋势 |
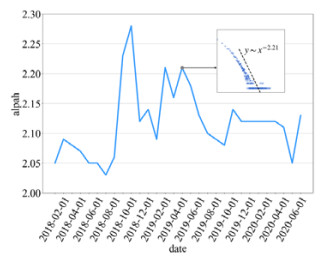
节点度分布的演化趋势如图 8所示. 使用幂律函数y~x−ɑ拟合闪电网络每月快照的节点度分布, 详细方法参见第3.3节. 最终得到了ɑ值的变化趋势, 如图 8所示. ɑ值越大, 拟合线的斜率越大, 度分布越不均匀, 闪电网络就越加中心化. 从图中可以看出, 闪电网络在中心化趋势和去中心化趋势之间随机波动. 尽管如此, ɑ值仍处于2~3之间, 表明闪电网络的度分布服从幂律分布. 总的来说, 闪电网络的节点度分布类似于无标度网络, 其各节点之间的连接状况(度数)具有严重的不均匀分布性. 网络中存在一些较为关键的重要节点, 所以业界对于其偏离区块链去中心化本质的担忧不无道理.
|
图 8 节点度分布变化趋势 |
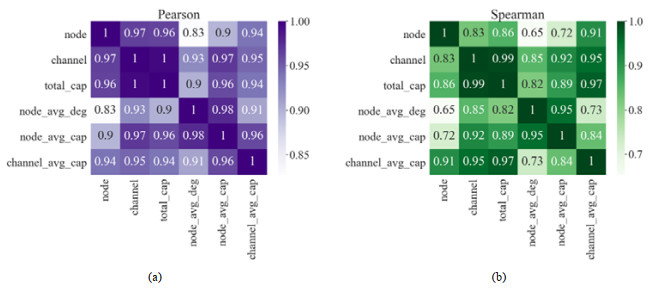
图 9展现了上述一些特征之间的Pearson相关系数和Spearman相关系数. 图中的node、channel、total_cap、node_avg_deg、node_avg_cap、channel_avg_cap分别代表节点数、通道数、网络总余额、节点平均度、节点平均余额、通道平均余额. Pearson相关系数是一种线性相关系数, 用于衡量两个变量间的线性相关程度. Spearman相关系数又称为秩相关系数, 是反映等级相关程度的统计分析指标. 通过观察发现, 这些特征之间的相关性很强. 通道数和网络总余额的Pearson相关系数是1.00, Spearman的相关系数是0.99, 可见它们之间的相关性非常强. 节点数和节点平均度之间的相关性是这些关系中相对较弱的, 但它们的Pearson相关系数仍达到了0.83, Spearman的相关系数为0.65, 属于强相关关系.
|
图 9 相关系数 |
4.2 通道存在时间
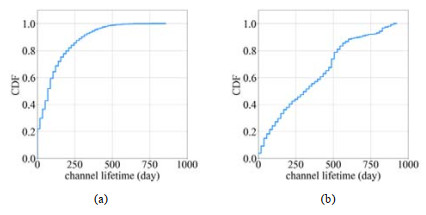
截至2020年7月22日, 闪电网络历史开通通道数为106 159, 其中, 67 500条通道已被关闭. 已关闭通道的平均存在时间为121天, 未关闭通道直至2020年7月22日的平均存在时间为342天. 图 10展示了已关闭通道和未关闭通道存在时间的累积分布函数图. 如图 10(a)所示: 超过20%的已关闭通道存在时间在1天以内, 近80%的已关闭通道存在时间不超过200天. 由图 10(b)可见: 超过半数的未关闭通道已存在时间少于400天. 此外, 本文还评估了通道存在时间与通道余额的关系. 在所有已关闭通道中, 其存在时间与其余额的Pearson相关系数和Spearman相关系数分别为−0.058和−0.001 4. 未关闭通道存在时间与其余额间的Pearson相关系数和Spearman相关系数分别为−0.104和−0.228. 由于通道数量较大且分布较为分散, 本文根据通道存在时间进行分类, 并分别对其计算与通道余额之间的关系, 见表 6和表 7.
|
图 10 已关闭通道和未关闭通道存在时间分布 |
| 表 6 已关闭通道存在时间与通道余额的相关性 |
| 表 7 未关闭通道存在时间与通道余额的相关性 |
可以看出: 在存在时间较久的通道中, 特别是在现存通道中, 存在时间与通道余额的关系更为强烈, 且呈负相关关系. 一些闪电网络的初始用户可能是为了验证其功能特性, 或者以尝试性的心理, 使用较小的金额开通通道, 而并不是为了满足支付交易的需求.
4.3 通道关闭方式支付通道的关闭会有不同的方式, 如下给出通道关闭的3种方式.
● 第1种称为mutual, 是一种合作的通道关闭方式, 通过广播资金交易的无条件花费并输出给每个对等点来实现;
● 第2种称为force, 是一种不合作的通道单向关闭方式, 通过广播承诺交易实现. 需要指出的是: 关闭时涉及的承诺交易比关闭交易本身规模更大(即效率更低), 且承诺交易中被广播的交易者在事先协商好的一段时间内不能取回在单向关闭的通道内的资金;
● 第3种称为penalty, 是被交易一方恶意撤销交易的支付通道的关闭, 该交易方通过广播想要撤销的交易的承诺交易来实现. 但是由于交易的另一方掌握了承诺交易的密钥, 则前述恶意通道关闭是无效的; 相反, 它还可以创建一个惩罚交易来让恶意撤销交易方损失交易抵押金额.
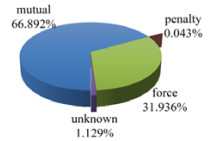
图 11展示了已关闭通道的关闭方式. 超过半数的已关闭通道以mutual方式被关闭, 以force方式被关闭的通道也占了一大部分, 仅有很少一部分通道以penalty方式被关闭.
|
图 11 通道关闭方式 |
5 闪电网络收费特征
无论是开通支付通道还是关闭支付通道, 都需要缴纳交易费用. 如表 8所示, 关闭支付通道的费用要高于开通支付通道的费用. 关于基础费用和费率的含义详见第1.2节中的解释. 基础费用的中位数和第90个百分位数均为1 sat. 然而, 关于费率的这3个值差异很大. 可以看出: 大部分节点的费率设置得非常小; 极少部分节点的费率设置得很大, 这部分节点的存在很可能是为了收取交易费用并获利.
| 表 8 关于费用的统计 |
下面给出关于基础费用和费率的详细分析.
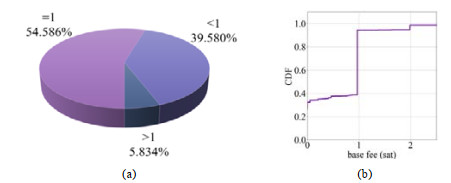
5.1 关于基础费用的分析基础费用的分布如图 12所示: 超过半数的通道将基础费用设置为1 sat; 仅有5.834%的通道基础费用设置大于1 sat, 且大部分将其设为2 sat.
|
图 12 基础费用的分布 |
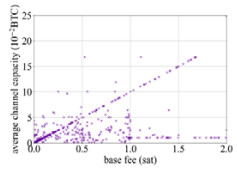
基础费用与通道余额的关系如图 13所示, 基础费用的范围取0−2 sat, 这涵盖了98.6%的通道. 可以看出: 在在一小部分通道中, 基础费用和通道余额呈线性关系; 但从总体上来看, 这两者之间的Pearson相关系数和Spearman相关系数分别为0.008 4和0.144 3, 说明基础费用和通道余额间的相关性很弱. 目前, 闪电网络用户对于基础费用的设置体现出一定的随机性和从众性.
|
图 13 基础费用与通道余额的关系 |
5.2 关于费率的分析
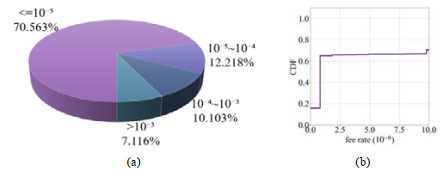
费率的分布如图 14所示: 超过70%的通道费率设置低于1×10−5, 且超过60%的通道将其设为1×10−6.
|
图 14 费率的分布 |
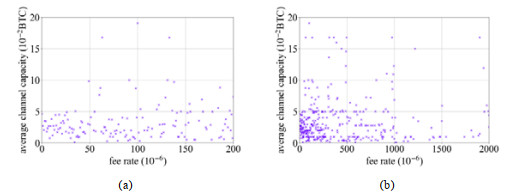
费率与通道余额的关系如图 15所示. 在图 15(a)中, 费率的范围取0−2×10−4, 这涵盖了83.6%的通道. 图 15(b)的费率范围取0−2×10−3, 涵盖了95%的通道. 费率和通道余额之间的Pearson相关系数和Spearman相关系数分别为−0.002 2和0.289 1, 说明两者有一定非线性的正相关性, 但相关性较弱.
|
图 15 费率与通道余额的关系 |
5.3 链上与链下交易费用的比较
为了深入了解交易通道网络收费的特点, 本节比较了链上和链下的交易费用. 具体方法在第2节中有所提及. 由于链上交易费用与许多因素相关且难以通过实验的方式获取到交易费用, 所以这里使用开通通道交易和关闭通道交易作为链上交易的代表. 本文通过计算开通通道和关闭通道的平均费用, 得到链上交易的平均费用, 为6 334.59 sat.
(1) 费用最小化
这里我们考虑费用最小化策略来进行路由支付, 结果见表 9. 随着交易金额的增大, 平均交易费用有一种粗略的成倍增大的趋势. 随着交易金额的增大, 能覆盖交易费用的可用通道数减少, 交易成功率会下降. 将链下和链上的平均交易费进行对比后发现: 链下交易比链上交易费用低得多, 即使当交易金额达到0.01 BTC时, 链下交易的平均费用也仅为664.049 sat, 比链上交易费用(6 334.59 sat)低了一个数量级. 进一步探究可知: 对于余额大于0.01 BTC的通道, 其平均基础费用为0.895 sat, 平均费率为6.103×10−3, 结合上文对费率分布的分析, 能够覆盖0.01 BTC的通道相对来说费率较高.
| 表 9 链下交易费用(费用最小化) |
(2) 路径长度最小化
这里我们考虑路径长度最小化策略来进行路由支付, 结果见表 10. 随着交易金额的增大, 平均交易费用显然比费用最小化策略增长得更明显. 成功率的数值及其变化趋势与费用最小化策略中的结果相似. 由表 10可知: 在此种交易策略下, 当交易金额小于500 000 sat时, 链下的平均交易费用远低于链上. 然而, 当交易金额增大到1 000 000 sat时, 由于可用于路由的通道数减少, 则平均交易费用急剧增大, 甚至高于链上的平均交易费用.
| 表 10 链下交易费用(路径长度最小化) |
除此之外, 无论是费用最小化策略还是路径长度最小化策略, 随着交易金额的增大, 平均路径长度都在减小. 这可能是因为那些余额相对较大的通道具有一定的聚集特征. 在闪电网络的最大连通分量中, 对所连通道中余额大于0.1 BTC的节点, 计算其平均最短路径长度, 得到的数值为1.59. 最大连通分量中所有节点的平均最短路径长度为3.52. 这个结果基本证实了上述观点.
6 相关工作据调研, 从拓扑学角度研究网络的方法已经较为成熟, 这些方法同样适用于闪电网络的研究. 本文首先从网络图分析的一般方法中得到一些启发, 然后重点关注比特币系统和闪电网络的图分析.
6.1 网络图分析的一般方法在网络图分析中, 有很多用于评估特殊属性的方法. 网络的扩展性可以通过多种方式进行研究. S-metric最先由LunLi等人在文献[13]中提出, 用于评估网络无标度的程度. 利用文献[9]中提到的方法, 基于实验数据可以证明网络的无标度性. 聚类系数和相关系数也是网络分析中的重要参数. 本文应用了文献[14−17]中的部分理论来解释数据含义. 此外, 中心性也是去中心化网络研究中较为重要的因素. 从文献[18−20]中得到启发, 本文采用了更好的方法来研究网络的内聚子群结构.
6.2 比特币系统的图分析近来的一些工作[21−27]细致研究了比特币的点对点覆盖. 一些文献[22−24]专注于研究和改进信息传播及其延迟. Miller等人[21]对于比特币网络的公共拓扑进行了调查, 并发现了一些有影响力的节点. 比特币交易图也吸引了众多研究者的关注[25−27]. 例如, DoritRon[26]对与比特币交易策略相关的交易图的统计特性进行了定量分析, 发现了用户的典型行为和隐私保护的方法. 本文采用Reid等人[28]的方法将闪电网络抽象为一个无向带权图, 其中每个节点代表一个参与者, 边代表支付通道, 其权值代表该通道中的余额.
6.3 闪电网络的图分析虽然闪电网络只投入使用不到3年, 但对它的研究有很多[2−7]. Martinazzi等人在文献[3]中研究了闪电网络的拓扑特征变化及其效率和同步性. 此外, 一些研究者在拓扑研究的基础上, 对安全问题也进行了探讨. 例如, 文献[4]分析了闪电网络对基于拓扑的攻击的恢复能力. 除了上述几个方面外, 闪电网络的路由问题也是研究的热门问题. Flare[5]是当前闪电网络的路由方法, 它的优点是寻找路径时效率很高. 当然还有许多其他具有不同优势的路由策略, 例如文献[6]中的多路径路由支付方案, 大大降低了交易费用. 此外, 还有一些对闪电网络中的交易所进行的模拟研究. Béres等人[7]为闪电网络设计了一个用于分析不同节点的路由成本和潜在收益的流量模拟器. 本文利用收集到的数据构建网络图进行全面的统计计算, 在此基础上给出了详实的解释和合理的推测. 此外, 本文还重点研究了闪电网络的收费机制, 通过进行交易仿真, 以对比闪电网络和比特币链上的交易费用.
7 结论本文基于具有高时效性的大量数据, 运用典型图分析方法对闪电网络进行研究, 对闪电网络中节点和通道的静态和动态拓扑特征进行了全面的分析. 利用上述静态和动态度量, 在闪电网络中进行节点聚类, 并根据聚类结果得到全面的结论和合理的推测. 全面研究了闪电网络的规模发展趋势、节点和通道特征以及节点的度分布等. 此外, 本文还特别对闪电网络的收费特征进行了详尽的研究. 通过在闪电网络中模拟费用最小化和路径长度最小化两种路由策略, 得到链下交易费用的估计; 通过进行合理的近似假设, 得到链上交易费用的统计; 最后, 通过两种交易费用的比较, 直观地证明了闪电网络出众的应用价值.
| [1] |
Poon J, Dryja T. The bitcoin lightning network: Scalable off-chain instant payments. 2016. https://lightning.network/lightning-network-paper.pdf
|
| [2] |
Seres IA, Gulyás L, Nagy DA, Burcsi P. Topological analysis of bitcoin's lightning network. arXiv preprint arXiv: 1901.04972, 2019.
|
| [3] |
Martinazzi S, Flori A. The evolving topology of the lightning network: Centralization, efficiency, robustness, synchronization, and anonymity. PloS One, 2020, 15(1): e0225966.
[doi:10.1371/journal.pone.0225966] |
| [4] |
Rohrer E, Malliaris J, Tschorsch F. Discharged payment channels: Quantifying the lightning network's resilience to topology-based attacks. In: Proc. of the IEEE European Symp. on Security and Privacy Workshops (EuroS & PW). IEEE, 2019.347-356.
|
| [5] |
Prihodko P, Zhigulin S, Sahno M, Ostrovskiy A, Osuntokun O. Flare: An Approach to Routing in Lightning Network. White Paper, 2016.
|
| [6] |
Di Stasi G, Avallone S, Canonico R, Ventre G. Routing payments on the lightning network. In: Proc. of the IEEE Int'l Conf. on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData). IEEE, 2018.1161-1170.
|
| [7] |
Béres F, Seres IA, Benczúr AA. A cryptoeconomic traffic analysis of bitcoins lightning network. arXiv preprint arXiv: 1911.09432, 2019.
|
| [8] |
LNchannels. https://ln.bigsun.xyz/
|
| [9] |
Clauset A, Shalizi CR, Newman MEJ. Power-law distributions in empirical data. In: Proc. of the SIAM Review. 2019.661-703.
|
| [10] |
Bitcoin's 'lightning torch' explained. https://www.coindesk.com/bitcoins-lightning-torch-has-blazed-through-37-countries-so-far
|
| [11] | |
| [12] | |
| [13] |
Li L, Alderson D, Doyle JC, Willinger W. Towards a theory of scale-free graphs: Definition, properties, and implications. Internet Mathematics, 2005, 2(4): 431-523.
[doi:10.1080/15427951.2005.10129111] |
| [14] |
Just W, Callender H, LaMar MD. Clustering coefficients. Technical Report, Dosegljivo: Ohio University, 2015. https://qubeshub.org/resources/741/download/ModuleCCQ.pdf
|
| [15] |
Lee J, Rodgers W, Nicewander A. Thirteen ways to look at the correlation coefficient. The American Statistician, 1988, 42(1): 59-66.
|
| [16] |
Taylor R. Interpretation of the correlation coefficient: A basic review. Journal of Diagnostic Medical Sonography, 1990, 6(1): 35-39.
[doi:10.1177/875647939000600106] |
| [17] |
Saramäki J, Kivelä M, Onnela JP, Kaski K, Kertesz J. Generalizations of the clustering coefficient to weighted complex networks. Physical Review E, 2007, 75(2): 027105.
[doi:10.1103/PhysRevE.75.027105] |
| [18] |
Estrada E, Rodriguez-Velazquez JA. Subgraph centrality in complex networks. Physical Review E, 2005, 71(5): 056103.
[doi:10.1103/PhysRevE.71.056103] |
| [19] |
Brandes U. A faster algorithm for betweenness centrality. Journal of Mathematical Sociology, 2001, 25(2): 163-177.
[doi:10.1080/0022250X.2001.9990249] |
| [20] |
Borgatti SP, Everett MG. A graph-theoretic perspective on centrality. Social Networks, 2006, 28(4): 466-484.
[doi:10.1016/j.socnet.2005.11.005] |
| [21] |
Miller A, Litton J, Pachulski A, Gupta N, Levin D, Spring N, Bhattacharjee B. Discovering bitcoin's public topology and influential nodes. 2015. https://allquantor.at/blockchainbib/pdf/miller2015topology.pdf
|
| [22] |
Neudecker T, Andelfinger P, Hartenstein H. Timing analysis for inferring the topology of the bitcoin peer-to-peer network. In: Proc. of the Int'l IEEE Conf. on Ubiquitous Intelligence & Computing, Advanced and Trusted Computing, Scalable Computing and Communications, Cloud and Big Data Computing, Internet of People, and SmartWorld Congress (UIC/ATC/ScalCom/CBDCom/IoP/SmartWorld). IEEE, 2016.358-367.
|
| [23] |
Decker C, Wattenhofer R. Information propagation in the bitcoin network. In: Proc. of the IEEE P2P 2013. IEEE, 2013.1-10.
|
| [24] |
Fadhil M, Owenson G, Adda M. A bitcoin model for evaluation of clustering to improve propagation delay in Bitcoin network. In: Proc. of the IEEE Int'l Conf. on Computational Science and Engineering (CSE) and IEEE Int'l Conf. on Embedded and Ubiquitous Computing (EUC) and the 15th Int'l Symp. on Distributed Computing and Applications for Business Engineering (DCABES). 2016.468-475.
|
| [25] |
Ober M, Katzenbeisser S, Hamacher K. Structure and anonymity of the bitcoin transaction graph. Future Internet, 2013, 5(2): 237-250.
[doi:10.3390/fi5020237] |
| [26] |
Ron D, Shamir A. Quantitative analysis of the full bitcoin transaction graph. In: Proc. of the Int'l Conf. on Financial Cryptography and Data Security. Springer, 2013.6-24.
|
| [27] |
Fleder M, Kester MS, Pillai S. Bitcoin transaction graph analysis. arXiv preprint arXiv: 1502.01657, 2015.
|
| [28] |
Reid F, Harrigan M. An analysis of anonymity in the bitcoin system. In: Proc. of the 3rd IEEE Int'l Conf. on Privacy, Security, Risk and Trust (PASSAT)/the 3rd IEEE Int'l Conf. on Social Computing (SocialCom). IEEE, 2011.1318-1326.
|
 2022, Vol. 33
2022, Vol. 33


