2. 智能机器人湖北省重点实验室(武汉工程大学), 湖北 武汉 430205
2. Hubei Key Laboratory of Intelligent Robot(Wuhan Institute of Technology), Wuhan 430205, China
植物是地球生态系统的重要组成部分, 是人类赖以生存的基础.许多植物在提供给人类食物、药物、建筑材料和纺织原料等方面发挥着重要的作用.据估计, 植物界现存大约450 000个物种, 直至2017年, 在维管植物中, 381 910个物种已被描述和命名[1].与此同时, 一些新的物种也不断地被发现.人类很早就开始研究植物的分类问题, 如古希腊哲学家、科学家将植物分为乔木、灌木和草本三大类.随着对植物分类研究的深入, 人们发现植物的局部特征, 如植物的叶片、花朵、果实对植物具有很好的表征特性, 可以作为分类的重要线索.而植物叶片以其存活时间较长、一年四季都可方便地采集, 且叶片薄而平坦的优点, 常被作为植物识别的重要特征和认识植物的主要参照器官.但由于许多植物物种的叶片的高度相似性, 如后文图 3和图 4中列出的不同种类的叶片, 使得通过人眼观察, 很难准确地辨识.
近些年来, 利用图像分析技术进行植物种类的识别, 是计算机视觉和图像处理领域中的一个研究热点.其中一个主要的方向是分析植物的叶片图像模式, 抽取有辨识力的叶片图像特征来区分叶片图像.叶片的图像模式有形状、纹理、叶脉和颜色等, 为植物的识别提供了非常有价值的线索.其中, 叶片的形状在叶片识别中扮演着重要的角色.它们既具有整体特征的差异性, 如一些物种的叶片呈剑形, 而一些则呈园形或椭圆形; 又有局部细节的不同, 如许多植物的叶片, 它们的叶片的边缘模式有着很大的不同, 一些物种有明显的锯齿, 而一些叶片的边缘是光滑的.不同品种的植物叶片的叶尖也呈现出不同的几何形态, 如一些物种的叶尖是凸尖的, 而一些物种的叶尖则是微凹的.因此, 近年来产生了大量的方法, 着眼于叶片的形状特征来识别叶片图像, 其中代表性的工作将在下一节介绍.
提取具有辨识力的叶片形状特征的挑战性在于:
(1) 叶片图像在采集的过程中, 叶片在图像平面的大小、方向和位置可能会发生改变, 叶片也可能会发生翻转, 这就要求描述算法抽取的特征必须满足对这些变换的不敏感性.
(2) 许多叶片形状具有非常小的类间差异性, 如有大量的不同种类的叶片都呈卵形或椭圆形, 这就需要特征抽取算法, 既能描述叶片形状整体的差异性, 又能刻画叶片细节上的差异.
(3) 由于叶片图像库的规模一般比较大, 需要算法具有较高的计算效率.
本文的研究工作着眼于基于形状特征的叶片图像识别问题, 提出了一种新的叶片形状描述和匹配方法.其主要贡献是:
(1) 提出了一种称为高斯卷积角的新的形状描述子, 其对平移、旋转、缩放和镜像变换的不变性, 从理论上得到了证明;
(2) 提出的高斯卷积角描述子通过不同尺度的高斯卷积, 有效地抽取了叶片形状的多尺度特征, 使得描述子具有强大的辨识能力, 且算法计算简单;
(3) 在当前流行的叶片图像数据集上进行了叶片图像的检索, 实验结果表明, 该方法优于其他同类方法.
1 相关工作本文聚焦于叶片形状的描述方法, 所以与本文研究工作相关的是近年来国内外提出的各种叶片形状描述子.这些方法可分为3类: 基于区域的方法、基于轮廓的方法、基于学习的方法.而基于轮廓的方法又分为基于边界点集的方法和基于曲线的方法.
基于区域的叶片形状描述方法是将叶片整个区域的像素点作为算法的输入, 将算法输出的特征向量作为描述子.Horaisová等人[2]将叶片形状转化成二值图像模式, 在其中提取二维傅里叶功率谱, 进行平移、缩放、旋转和镜像等操作, 该方法在植物叶片分类中取得了很好的效果.考虑到很难从叶片轮廓中找到明显的曲率点, Lee等人[3]认为: 一些基于区域的特征, 例如纵横比、紧密度、质心和水平或垂直投影等, 对叶片图像的识别更为可靠.文献[4]提出用快速Curvelet变换得到3个变换系数, 再对每一个系数, 用其第1个不变矩表征形状, 由此得到一个三维的形状特征向量.文献[5]提出了一种结构积分变换(structure integral transform), 不同于图像沿直线进行投影的Radon变换, 该方法将形状图像沿一对正交直线进行投影, 用图像在两个正交方向上的直线投影长度得到一个复数来表征图像区域的内部结构, 相较于基于Radon变换的描述子, 对形状的表征能力更强, 且满足对平移、旋转和缩放的不变性.
叶的轮廓包含了叶片的边缘、顶点和基质这些丰富的鉴别信息[6], 这些信息通常被认为是物种识别的主要线索.因此, 国内外相关学者基于这些鉴别信息提出了两类用于植物识别的叶片轮廓描述方法, 主要包括基于边界点集的描述方法和基于曲线的描述方法.
基于边界点集的描述方法是将目标边界(包括内边界和外边界)看成一个无序的点集, 直接抽取点集的几何特征作为形状的描述子[7].形状上下文[8]是一个著名的基于边界点集的描述子.该方法对每一个边界采样点, 构造对数极坐标直方图, 以统计所有其他边界采样点, 相对于它的空间分布关系.Ling等人[9]定义两个轮廓采样点之间的内部距离为一个点到另外一个点的所有只经过轮廓所围区域的路径的长度最小值.不同于文献[8]提出的欧式距离产生形状上下文, 该方法用轮廓采样点之间的内部距离构建形状上下文描述子.其优点是描述子对目标的肢体变化不敏感, 且能有效地描述目标的结构信息.该方法已有效地应用于研发植物叶片识别系统[10]. Backes等人[11]将形状轮廓建模成一个复杂网络, 并通过网络的动态演化, 用网络的度和联合度作为形状特征, 构建特征向量来描述叶片形状.该方法它不仅满足尺度和旋转的不变性, 而且不依赖于轮廓的拓扑结构.
基于曲线的描述方法是将叶片轮廓作为曲线, 通过测量其曲线的几何特性来描述形状.曲率尺度空间(curvature scale space, 简称CSS)[12]是一种基于轮廓曲率测量的描述子, 且被MEPG-7[13]推荐为标准的轮廓描述子.一个形状图像的轮廓线通过不同宽度的高斯卷积, 得到曲率过零点的变化轨迹, 形成CSS图像作为形状描述子.文献[13]提出了一种CSS表示的泛化方法, 用于识别具有自遮挡的轮廓, 并成功地用于对菊花叶片的识别.对曲线曲率的测度一般使用的是微分技术, 但其局限性是噪声比较敏感.Manay等人[14]提出运用不同的核函数来进行对目标轮廓的积分运算, 产生形状描述不变量, 并具有对曲线曲率度量的等效性和对噪声干扰的鲁棒性. Kumar等人[15]用该思路构造圆盘积分不变量和圆周积分不变量, 产生描述叶片形状特征的直方图, 用于研发叶片图像的识别系统.除了曲线的曲率特性, 曲线的一些其他几何特征也可用来产生描述子.Hu等人[16]提出用多尺度距离矩阵(multiscale distance matrix, 简称MDM)进行快速叶片识别, 该方法用叶片轮廓的每一对采样点之间的欧式距离或内部距离, 产生满足对相似变换不变的距离矩阵, 作为形状描述子.分层弦切法(hierarchical string cuts, 简称HSC)[17]通过用弦对轮廓片段的切割, 抽取轮廓片段上的点相对于弦的几何空间分布信息, 以描述轮廓片段的几何结构特征.该方法通过改变轮廓片段的长度, 自然地构建了一个多尺度的轮廓弦切描述子.该方法的主要优点是运行非常快, 描述能力非常强, 适用于需要大规模的数据库图像检索任务.
近年来, 一些基于学习的方法也被用来产生叶片形状描述子.受词袋模型(bag-of-words)[18, 19]的启发, Wang等人[20]提出将叶片形状拆分成轮廓片段, 用它们的形状上下文描述子(shape context)构成形状编码; 然后用训练样本的形状编码, 通过K均值聚类算法, 用得到的类中心的集合生成轮廓线片段的码本; 最后, 用码本对形状图像进行编码描述.该算法得到的描述子具有鲁棒、紧致的特性, 且精确地描述了包括轮廓线片段的空间布局信息.Zhao等人[6]提出用字典学习技术[21]去收集叶片形状的有用模式, 描述一个叶片形状就简化为在收集的形状模式集上的分布直方图上计算形状特征.该方法最大的优点是能对单叶叶片图像和复合叶片图像都进行有效的识别.Zeng等人[22]提出一种基于距离的融合稀疏表示和局部约束字典学习的鲁棒叶片识别新方法, 该方法不仅提高了叶片识别精度, 而且识别速度也很快.针对描述图像内容的高维特征的数据冗余和噪声干扰问题, Li等人[23]组合利用谱聚类和冗余分析, 提出一种带冗余约束的非负谱分析无监督特征选择方法.该方法可直接鉴别出最有用和冗余约束的、具有区分力的特征子集.通过在包括人脸数据、手写数字数据、目标图像数据的算法性能测试, 验证了该方法的有效性.近来, Lee等人[24]将深度学习应用于植物叶片图像的分类问题.该方法使用卷积神经网络(CNN)直接从输入数据的原始表示中学习有用的叶片特征, 并用反卷积网络(DN)方法解释获取的CNN特征的叶片描述能力.
本文提出的方法属于传统的非学习方法, 即产生叶片图像描述子不需要训练样本的参与, 直接抽取叶片图像特征用于叶片的相似性检索.因此, 本文提出的方法跟基于学习的方法相比, 具有计算效率高、且抽取的特征不依赖于训练样本的优点.与本文最相近的是各类基于轮廓线的形状描述方法, 不同之处在于: (1) 本文提出的描述子是通过高斯函数与轮廓线函数的左右卷积产生高斯卷积角不变量, 不同于描述轮廓点的相对分布的描述子[8, 9, 17], 刻画轮廓线曲率的圆盘积分不变量和圆周积分不变量[14, 15], 以及基于轮廓点距离的描述子[16], 该方法不仅满足对旋转、缩放和平移的不变性, 而且满足对镜像变换的不变性; (2) 多尺度描述的产生机制不同, 本文提出的方法用高斯函数的宽度作为尺度变量, 它不同于现有的用弧长作为尺度变量的方法[16, 17]以及用径向距离作为尺度变量的方法[8, 9, 14, 15].
2 高斯卷积角不变量本节给出了我们提出的用于描述叶片形状的高斯卷积角不变量, 以及基于该描述子的叶片形状差异性度量方法.
2.1 高斯卷积角对于给定的一个叶片的形状轮廓Ω, 数学上可将其用弧长参数化形式[25]表示为z(t)=x(t)+j·y(t), 其中,
| $\xi _\sigma ^ - (t) = \int_{ - \frac{1}{2}}^0 {{G_\sigma }(r) \cdot (z(t + r) - z(t))dr} $ | (1) |
| $\xi _\sigma ^ + (t) = \int_0^{\frac{1}{2}} {{G_\sigma }(r) \cdot (z(t + r) - z(t))dr} $ | (2) |
其中,
| ${G_\sigma }(r) = \frac{1}{{\sqrt {2\pi } \sigma }}{e^{ - \left( {\frac{{{r^2}}}{{2{\sigma ^2}}}} \right)}}$ | (3) |
在公式(3)中, σ是尺度参数.
我们将向量
| ${\theta ^\sigma }(t) = \varGamma \left( {\frac{{\xi _\sigma ^ - (t)}}{{\xi _\sigma ^ + (t)}}} \right)$ | (4) |
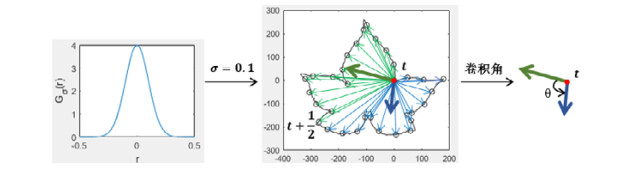
其中, Γ(·)是计算复数的辐角.图 1给出了用尺度参数σ=0.1的一维高斯函数与叶片轮廓点z(t)的左、右邻域的向量分别进行卷积产生的高斯卷积角的示意图.
|
Fig. 1 Illustration of generating a Gaussian convolution angle. Left: Curve of the Gaussian function with σ=0.1; Middle: Left and right neighborhood vectors of the contour point z(t); Right: Resulting Gaussian convolution angle 图 1 用σ=0.1的一维高斯函数(左图)与轮廓点z(t)的左右邻域向量(中图) 分别进行卷积产生高斯卷积角(右图)的示例 |
我们使用高斯卷积角产生描述子ωσ(t), 定义如下:
| $ \omega^{\sigma}(t)=\sin \left(\theta^{\sigma}(t)\right) $ | (5) |
依上式, 我们显然有ωσ(t)∈[-1, 1], 且ωσ(t)大于0、等于0和小于0分别描述轮廓线在尺度σ下的凸、平和凹的特性.值得指出的是, 高斯函数Gσ在高斯卷积角的产生过程中扮演着权重分配的角色.依据高斯函数的性质, 离轮廓点z(t)越近的邻域向量(即|r|值越小的向量), 获得的权重越大.
2.2 多尺度描述因为人的视觉系统对目标物体具有多尺度的感知特性, 所以在计算机视觉研究中, 构造多尺度的描述子是提高识别精度的一个常用的技术路线.针对叶片图像识别问题, 从不同层级来对叶片形状进行描述, 可以提取到叶片形状的全局特征和局部细节.由高斯卷积角的定义, 高斯函数的尺度参数σ可以自然地帮助我们将描述子ωσ(t)扩展到多尺度描述.下面我们通过讨论尺度参数σ的变化对ωσ(t)的描述行为的影响, 来分析高斯卷积角的多尺度描述能力.
一维高斯函数
一般叶片的识别可依据其粗粒度的特征进行大致的分类, 如一些不同种类的叶片会有明显不同的叶形, 诸如椭圆形、扇形、心形、菱形、掌形等, 但很多不同种类的叶片在粗粒度特征上具有很大的相似性, 如一些不同种类的叶片都呈椭圆形或卵形, 更需要通过细粒度的特征进行精确的识别, 如它们的细粒度特征, 叶片的锯齿, 可作为主要的识别线索.考虑到σ≥0.2的曲线都呈扁平状, 且它们非常接近, 我们限定σ的取值区间为(0, 0.2).为使描述子对局部细节的描述得到加强, 同时又考虑粗粒度特征, 我们在该区间为σ取如下k个值:
| $ \sigma_{1}=2^{-3}, \sigma_{2}=2^{-4}, \ldots, \sigma_{k}=2^{-(k+2)} $ | (6) |
作为高斯卷积角的多尺度取值, 该尺度安排是在区间(0, 0.2)的一个非均匀取值, 使得σ取值点在区间的前半部(小的取值)更密集, 后半部分(大的取值)更稀疏.通过改变高斯卷积角的尺度参数σ, 我们获得了由以下定义的k维高斯卷积角特征向量:
| $ \omega(t)=\left(\omega^{\sigma_{1}}(t), \omega^{\sigma_{2}}(t), \ldots, \omega^{\sigma_{k}}(t)\right) $ | (7) |
这里, 我们称其为多尺度高斯卷积角.
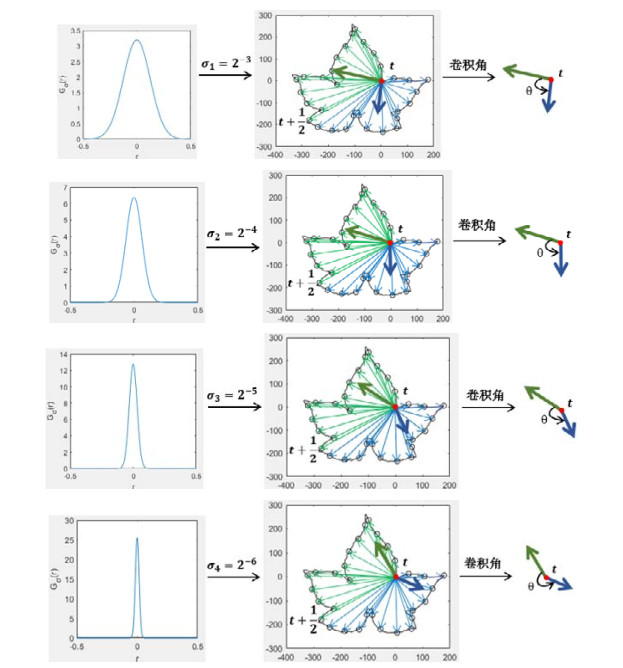
我们用一幅叶片图像的多尺度高斯卷积角为例(见图 2, 尺度参数的取值为σ1=2-3, σ2=2-4, σ3=2-5和σ4=2-6), 来说明多尺度的描述行为.该图给出了4个尺度σ1, σ2, σ3, σ4的高斯卷积角.我们多尺度地观察该叶片图像, 观察z(t)左右邻域的整个轮廓线, 可看出轮廓线是凸的, 且弯曲程度很大, 此时, 高斯卷积角呈现一个比较小的角; 而当我们的视野聚焦于z(t)的邻域越来越小时, 会发现轮廓弯曲程度变小, 最后由凸变凹, 此时高斯卷积角呈现为一个大于180°的角.可以看出, 多尺度高斯卷积角的描述行为与我们的视觉的多尺度观察效果具有一致性.
|
Fig. 2 An example of showing the proposed Gaussian convolution angles at various scales 图 2 多尺度高斯卷积角的一个例子 |
2.3 不变性分析
下面我们分析高斯卷积角描述子在相似性变换和镜像变换中的行为.
(1) 相似性变换
相似性变换包括平移、旋转和缩放变换.一个好的描述子应满足对相似性变换的不变性.下面我们从理论上证明所提出的高斯卷积角描述子对相似性变换满足不变性.
证明: 对于发生相似性变换的轮廓Ω的参数方程, 可形式化地定义为
| $\dot z(t) = \lambda \cdot R \cdot z(t) + T$ | (8) |
其中, λ > 0是缩放因子, R=cosa+j·sina是旋转角度a的旋转变换, T=tx+j·ty表示平移因子.由高斯卷积角的定义, 我们有:
| $\begin{gathered} \dot \xi _\sigma ^ - (t) = \int_{ - \frac{1}{2}}^0 {{G_\sigma }(r) \cdot (\dot z(t + r) - \dot z(t)){\rm{d}}r} = \int_{ - \frac{1}{2}}^0 {{G_\sigma }(r) \cdot (\lambda \cdot R \cdot z(t + r) + T - \lambda \cdot R \cdot z(t) - T){\rm{d}}r} \\ = \lambda \cdot R\int_{ - \frac{1}{2}}^0 {{G_\sigma }(r) \cdot (z(t + r) - z(t)){\rm{d}}r} = \lambda \cdot R \cdot \xi _\sigma ^ - (t) \\ \end{gathered} $ | (9) |
同理可得:
| $\dot \xi _\sigma ^ + (t) = \lambda \cdot R \cdot \xi _\sigma ^ + (t)$ | (10) |
因此, 我们有:
| ${\dot \theta ^\sigma }(t) = \varGamma (\dot \xi _\sigma ^ - (t)/\dot \xi _\sigma ^ + (t)) = \varGamma (\xi _\sigma ^ - (t)/\xi _\sigma ^ + (t)) = {\theta ^\sigma }(t)$ | (11) |
则可推出:
| ${\dot \omega ^\sigma }(t) = \sin ({\dot \theta ^\sigma }(t)) = \sin ({\theta ^\sigma }(t)) = {\omega ^\sigma }(t)$ | (12) |
从以上推导, 我们可以得出, 高斯卷积角描述子满足对于相似性变换的不变性.
(2) 镜像变换
证明: 不失一般性, 我们假设叶片形状在y轴上发生镜像变换, 则形状轮廓Ω的参数方程的镜像版本为
| $\dot z(t) = - x(1 - t) + j \cdot y(1 - t) = - \overline {z(1 - t)} $ | (13) |
这里,
| $\begin{gathered} \dot \xi _\sigma ^ - (t) = \int_{ - \frac{1}{2}}^0 {{G_\sigma }(r) \cdot (\dot z(t + r) - \dot z(t)){\rm{d}}r} \\ {\rm{ }} = \int_{ - \frac{1}{2}}^0 {{G_\sigma }(r) \cdot [ - \overline {z(1 - t - r)} + \overline {z(1 - t)} ]{\rm{d}}r} \\ {\rm{ }} = \overline {\int_{ - \frac{1}{2}}^0 {{G_\sigma }(r) \cdot [ - z(1 - t - r) + z(1 - t)]} {\rm{d}}r} \\ \end{gathered} $ | (14) |
将上式的r换成-r, 可推得:
| $\dot \xi _\sigma ^ - (t) = \overline {\int_0^{\frac{1}{2}} {{G_\sigma }(r) \cdot [z(1 - t + r) - z(1 - t)]{\rm{d}}r} } = \overline {\xi _\sigma ^ + (1 - t)} $ | (15) |
同理可得:
| $\dot \xi _\sigma ^ + (t) = \overline {\int_{ - \frac{1}{2}}^0 {{G_\sigma }(r) \cdot [z(1 - t + r) - z(1 - t)]{\rm{d}}r} } = \overline {\xi _\sigma ^ - (1 - t)} $ | (16) |
因此, 我们有:
| ${\dot \theta ^\sigma }(t) = \varGamma (\dot \xi _\sigma ^ - (t)/\dot \xi _\sigma ^ + (t)) = \varGamma (\overline {\xi _\sigma ^ + (1 - t)} /\overline {\xi _\sigma ^ - (1 - t)} ) = \varGamma (\overline {\xi _\sigma ^ + (1 - t)/\xi _\sigma ^ - (1 - t)} )$ | (17) |
因对于一个复数z, 我们有
| ${\dot \theta ^\sigma }(t) = {\theta ^\sigma }(1 - t)$ | (18) |
则高斯卷积角描述子的镜像变换版本为
| ${\dot \omega ^\sigma }(t) = \sin ({\dot \theta ^\sigma }(t)) = \sin ({\theta ^\sigma }(1 - t)) = {\omega ^\sigma }(1 - t)$ | (19) |
上述推导表明: 镜像变换只是改变了高斯卷积角描述子的弧长参数t, 将其由t变为了1-t.
下面我们利用上述性质, 构造满足对镜像变换不变的描述子.由公式(7), 我们已将每一个轮廓点z(t)的k个尺度的高斯卷积描述子组合成了一个k维的特征向量ω(t), 显然, 我们有
| $ \varPsi=\{\omega(t), 0 \leqslant t<1\} $ | (20) |
显然, 对于该集合的镜像变换版本
| $\dot \varPsi = \{ \dot \omega (t), 0 \leqslant t < 1\} = \{ \omega (1 - t), 0 \leqslant t < 1\} = \{ \omega (t), 0 \leqslant t < 1\} = \varPsi $ | (21) |
即Ψ满足镜像变换的不变性.我们将高斯卷积角集合Ψσ作为最终的形状描述子.
2.4 差异性度量我们已将叶片形状描述成一个高斯卷积角特征向量的集合Ψ={ω(t), 0≤t < 1}, 那么比较叶片形状A和叶片形状B的差异, 可以通过计算它们的高斯卷积角特征向量集合ΨA和ΨB的Hausdorff距离来进行度量.我们首先将轮廓线均匀采样T个点, 即从弧长参数区间[0, 1], 均匀采样T个值: t1, t2, …, tT.则两个集合可表示为ΨA={ωA(tm), m=1, 2, …, T}和ΨB={ωB(tn), n=1, 2, …, T}.这里, 我们采用文献[26]提出的增强型Hausdorff距离来度量集合ΨA和ΨB的距离.
首先, 我们定义两个集合的任意两个元素ωA(tm)和ωB(tn)的距离为
| $ d\left(\omega_{A}\left(t_{m}\right), \omega_{B}\left(t_{n}\right)\right)=\left\|\omega_{A}\left(t_{m}\right)-\omega_{B}\left(t_{n}\right)\right\|_{1} $ | (22) |
这里, ||·||1是L1范数.然后, 我们定义集合ΨA到集合ΨB的距离为
| $ D\left(\varPsi_{A}, \varPsi_{B}\right)=\frac{1}{T-\eta_{ A}} \sum\limits_{m=1}^{T} \min _{n=1, \ldots, T} d\left(\omega_{A}\left(t_{m}\right), \omega_{B}\left(t_{n}\right)\right) $ | (23) |
其中, ηA的计算步骤如下.
(1) 定义一个数组ζ(1:T), 并设置每个元素为-1;
(2) 对于集合ΨA中的每个元素ωA(tm), 在集合ΨB中找到其最佳匹配, 即与其距离最小的元素ωB(tn), 作累加操作: ζ(n)
(3) 将数组ζ中所有的值大于0的元素相加赋值给ηA.
容易看出, 变量ηA的值范围为0到T-1的整数.当ηA=0时, 集合ΨA中的所有元素匹配到了集合ΨB中的不同元素, 即产生的是一对一映射, 这是理想的匹配情况; 而ηA=T-1表示集合ΨA中的所有元素都匹配到了集合ΨB中的同一个元素; 而0 < ηA < T-1, 则表示存在集合ΨA中的不同元素匹配到了集合ΨB中的同一元素的情况.
以相同的方式计算从集合ΨB到集合ΨA的距离D(ΨB, ΨA), 则叶片形状A和形状B之间的差异度量定义为
| $ {Diff}(A, B)=\max \left(D\left(\varPsi_{A}, \varPsi_{B}\right), D\left(\varPsi_{B}, \varPsi_{A}\right)\right) $ | (24) |
若Diff(A, B)的值越大, 则表示形状A和形状B差异越大; 反之, 则越小.
3 算法时间复杂度分析本文提出的方法的计算时间复杂度分为两个部分: 一个是特征抽取的计算时间, 另一个是特征匹配的计算时间.在特征抽取阶段, 在给定的尺度下, 对于每一个轮廓点, 通过计算其左右卷积向量得到高斯卷积角的计算时间复杂度为O(T), 因此, 计算所有T个轮廓点的高斯卷积角的计算时间复杂度为O(T2), 则所有轮廓点的k个尺度的高斯卷积角的计算复杂度为O(kT2), 即为特征抽取阶段的计算时间复杂度.
在特征匹配阶段, 通过计算两个形状的高斯卷积角特征向量集合的增强Hausdorff距离来比较两个形状的差异.其中, 计算两个高斯卷积角特征向量集合的任意两个元素的距离(公式(22))的计算复杂度为O(k), 计算公式(23)中的
为了评估本文所提出的高斯卷积角形状描述方法的性能, 我们用公开的植物叶片图像数据库CVIP100数据集[17]和中欧木本植物(MEW)数据集[27]测试本文提出的算法的叶片图像检索性能, 用公开的Kimia形状数据集[28]的形状检索实验评估本文提出的方法的通用性.为了检验本文所提出的方法的有效性和优越性, 我们选择了4种具有较高性能的形状检索算法进行实验比较, 它们是内部距离形状上下文(IDSC+DP)[9]、多尺度距离矩阵(MDM)[16]、高度函数(height function)[29]和分层弦切法(HSC)[17].此外, 在实验中, 我们还将本文提出的高斯卷积角描述子与近年来提出的深度特征进行检索性能对比, 我们选用了近年来比较先进与流行的预训练网络模型VGGNet-19[30]和RESNet-152[31].实验平台是一台CPU为Intel(R) Core(TM) i5, 操作系统为Windows 10, 内存为8GB的个人计算机, 实现算法的编程工具为MATLAB R2014a.而运行两个深度学习方法的平台是CPU为Intel(R) Core(TM) i9-9900k, 内存为32GB, 显卡为NVIDIA RTX 2080的计算机.本文提出的方法的参数设置为: 叶片轮廓均匀采样的点的个数为256, 所使用的尺度个数k设置为8.
4.1 数据集我们进行叶片图像检索的第1组实验采用的测试集是CVIP100叶片图像库[17].该图像库中的叶片主要采自国内, 包含从100种植物中收集的1 200张叶片图像, 每种有12个样本.图 3给出了CVIP100的所有100种叶片的示例, 观察该图可以看出: 许多样本具有很大的形状相似性, 如同为椭圆或卵形, 凭人的视觉观察, 很难区分它们.

|
Fig. 3 Example leaf images of 100 plant species form the CVIP100 dataset[17] 图 3 CVIP100数据集中的100种叶片样本图像示例[17] |
我们用于评估算法性能的第2组实验是在中欧木本植物(MEW)数据集[27]上进行的.该图像库中的叶片采自中欧地区原生或经常种植的153类树木和灌木, 每类至少有50个样本, 共计9 745个样本.其中, Hedera_helix分为可育和不育形式, Maclura_pomifera分为雌性和雄性, 因此, 151种植物物种产生了153种可识别的类别.图 4给出了MEW数据集中所有153种叶片的示例.从该图可以看出: 由于样本都是采自木本植物, 不同种类的大多数叶片形状差异非常小, 通过人眼观察很难辨识.
为了验证本文提出的高斯卷积角形状描述方法的通用性, 我们的第3组实验是在Kimia[28]形状数据集上进行的.该数据集是目前被广泛使用的标准形状图像库, 它包含9个类别的形状, 每个类别有11个样本, 如图 5所示, 属于同一类的样本存在旋转、缩放、局部遮挡、边缘扭曲、类内形变等复杂的形状变化, 从而使得识别更具挑战性.
4.2 性能评估方法
这里, 我们采用信息检索的标准性能评估方法——平均精度均值(mean average precision, 简称MAP)[32]来评估算法的检索性能.设数据库中有N个图像, 将每一个样本qi作为查询图像, 与数据库中的所有图像进行匹配, 共计N次匹配.将匹配结果按公式(24)定义的差异度量值, 由小到大排序, 得到该查询图像的检索结果.设该查询图像qi在数据库中有Qi个同类样本, 并计它们在检索排序列表中的位置为
| $a{p_i} = \frac{1}{{{Q_i}}}\sum\nolimits_{m = 1}^{{Q_i}} {\frac{{{S_m}}}{{{P_m}}}} $ | (25) |
则MAP的计算公式定义为
| $MAP = \frac{1}{N}\sum\nolimits_{i = 1}^N {a{p_i}} $ | (26) |
(1) CVIP100叶片数据集
由表 1可以看出: 本文所提出的方法获得了89.27%的MAP分数, 分别比IDSC+DP、MDM、Height Function、HSC、VGGNet-19和RESNet-152方法高出了8.74%, 17.77%, 5.02%, 3.19%, 8.73%, 6.16%.在平均检索时间方面, 本文所提出的方法运行速度快于IDSC+DP、MDM、Height Function方法, 慢于HSC和两种深度学习方法VGGNet-19[30]和RESNet-152[31].但这里报告的深度学习方法的计算时间不包含网络训练的时间, 而且深度特征的计算运行在高性能计算平台.综合考虑检索精确度和检索效率, 本文提出的方法性能最优.
| Table 1 Comparison of MAP scores of various methods on CVIP100 dataset 表 1 各种方法在CVIP100叶片图像测集上的MAP值的对比 |
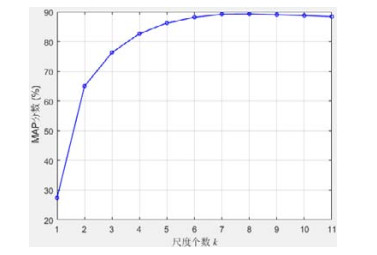
本文所提出的方法有两个重要的参数: 一个是尺度个数k, 一个是轮廓点的采样个数T.为研究它们对算法性能影响, 我们在CVIP100数据集上进行了另外两组实验.一组实验是研究尺度个数k的不同取值对检索结果的影响.我们将尺度个数k从1取值到11, 得到对应的检索结果, 将实验结果绘成折线图, 如图 6所示.由该图我们可以看出: 当只取一个尺度时, 即取尺度安排中的最大尺度σ=2-3, MAP值只有27.43%.这是因为此时描述子主要侧重于粗粒度特征, 而对叶片图像的细节信息描述能力不足.当增加尺度个数k, 细粒度特征的描述能力持续得到加强, 反映图像检索精度的MAP值也持续提升.当k取到8时, MAP值达到最高值为89.27%.而当k继续取大于8的值时, 我们发现MAP值有所降低.这是因为k过大, 描述子将会引入更多的细粒度特征, 使得描述子中细粒度特征所占的比重越来越大, 粗粒度特征的作用会被逐渐忽略, 即描述子会过度聚焦于细节信息, 而忽略了叶片图像的整体特征.另一方面, 一般细粒度特征对噪声比较敏感, 而k过大, 也会减弱描述子的粗粒度特征对噪声的压制作用.为保持描述子对粗细两类特征描述的平衡性, 我们经验的选取k=8.
|
Fig. 6 MAP scores of the leaf shape description method of Gaussian convolution angles obtained by taking different values of the scale levels k on the CVIP100 dataset 图 6 在CVIP100数据集上, 高斯卷积角叶片形状描述方法在尺度个数k取不同值时获得的MAP分数 |
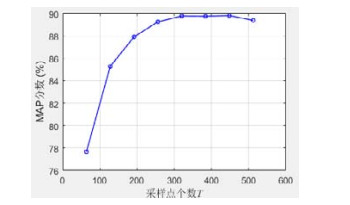
另一组实验是研究不同的采样点个数对检索性能的影响.我们将尺度个数k固定为8, 采样点个数T在[64,512]区间以64的步长均匀取8个数值即64, 128, 192, 256, 320, 384, 448, 512, 得到对应的MAP值, 将实验结果绘成折线图, 如图 7所示.
|
Fig. 7 MAP scores of the leaf shape description method of Gaussian convolution angles obtained by taking different number of the sampling points on the CVIP100 dataset 图 7 在CVIP100数据集上, 高斯卷积角叶片形状描述方法在采样点个数取不同值时获得的MAP分数 |
由该图我们可以看出: 当采样点个数为64, 128, 192时, 对应的MAP值分别为77.67%, 85.29%, 87.93%;而当采样点个数大于等于256时, MAP值在89%~90%区间波动.这是因为当采样点个数较小时, 提取的轮廓线会丢失大量的细节信息, 描述子引入的都是粗粒度特征, 所以获得的MAP值较低; 当采样点个数越来越大时, 提取的轮廓线越来越细致, 随着采样点个数的持续增加, 形状的细致的特征可以被描述子抽取到, 但一般细粒度特征对噪声比较敏感, 从而使得MAP值在[89,90]区间有细微的波动.而且采样点个数T过大, 也会增大计算的开销.因此, 平衡检索精度和计算效率, T取256比较合适.
(2) 中欧木本植物(MEW)数据集
本组实验的参数设置和前组实验相同, 用于算法性能比较的其他方法也与前组实验相同.表 2列出了本文提出的方法与其他参与比较的6种方法在MEW测试集上的检索结果的MAP值和平均检索时间.从该表可以看出: 本文提出的方法获得了62.10%的最佳MAP值, 比排名第二的方法VGGNet-19高2.99%, 并且比其他对比方法高出超过6%.该实验结果进一步验证了本文提出的方法在叶片图像检索中的有效性, 以及相较于其他形状图像检索方法的优越性.在检索速度方面, 跟前组实验一致, 而综合考虑检索精确度和检索效率, 本文提出的方法性能最优.
| Table 2 Comparison of MAP scores of various methods on MEW dataset 表 2 各种方法在MEW叶片图像测试集上的MAP值的对比 |
(3) Kimia形状数据集
本组实验旨在测试本文提出的方法的通用性和鲁棒性.实验中的参数设置和算法性能比较的其他方法与前两组实验相同.表 3列出了本文提出的方法与其他参与比较的6种方法在Kimia形状数据集上的检索结果的MAP值.从该表可以看出: 本文提出的方法获得了93.73%的MAP值, 高于除Height Function之外的其他方法.但由于Height Function采用基于动态规划的点到点的匹配, 使得其计算复杂度要高于本文提出的方法.该组实验结果表明, 本文提出的方法能适用于一般的形状图像检索任务.
| Table 3 Comparison of MAP scores of various methods on Kimia dataset 表 3 各种方法在Kimia图像数据集上的MAP值的对比 |
5 结论
本文提出了一种新的叶片形状描述方法——高斯卷积角, 以应用于解决具有挑战性的叶片图像检索任务.该方法通过轮廓点的左右邻域向量与不同宽度的高斯函数的卷积, 产生描述轮廓弯曲特性的多尺度角度特征, 再用多个尺度的高斯角, 构成高斯角特征向量, 最后组合所有轮廓采样点的高斯角特征向量, 生成一个高斯角特征向量集合, 作为叶片形状描述子.通过比较两个叶片形状的高斯角特征向量集合的增强型Hausdorff距离, 来度量两个叶片形状之间的差异.本文所提出的高斯卷积角描述子具有以下优良特性: (1) 它满足对平移、旋转、缩放和镜像变换的不变性, 本文从理论上证明了这一优良特性; (2) 它是一种多尺度的描述子, 由粗到细提取叶片的形状特征, 这使得它对叶片图像具有强大的辨别能力; (3) 该算法计算简单, 易于实现.我们在两个公开的叶片图像测试集——CVIP100叶片图像库和MEW叶片图像库, 都取得了比其他同类方法更高的检索精确率(在CVIP100和MEW上分别高出3.19%和2.99%以上).该实验结果验证了本文提出的方法在叶片图像检索中的有效性和相较于其他同类方法的优越性.值得指出的是: 本文的方法虽然是针对叶片图像提出的, 但其也具有适应于一般的形状识别任务的潜力.我们用公开的Kimia形状数据集测试了其应用于一般形状识别任务的潜力.进一步地研究和发展该方法, 以应用于其他的形状识别任务, 将是今后进一步的研究的目标.
| [1] |
Pimm SL, Joppa LN. How many plant species are there, where are they, and at what rate are they going extinct?. Annals of the Missouri Botanical Garden, 2015, 100(3): 170-176.
[doi:10.3417/2012018] |
| [2] |
Horaisová K, Kukal J. Leaf classification from binary image via artificial intelligence. Biosystems Engineering, 2016, 142: 83-100.
[doi:10.1016/j.biosystemseng.2015.12.007] |
| [3] |
Lee CL, Chen SY. Classification of leaf images. International Journal of Imaging Systems and Technology, 2006, 16: 15-23.
[doi:10.1002/ima.20063] |
| [4] |
Chaki J, Parekh R, Bhattacharya S. Plant leaf recognition using texture and shape features with neural classifiers. Pattern Recognition Letters, 2015, 58: 61-68.
[doi:10.1016/j.patrec.2015.02.010] |
| [5] |
Wang B, Gao Y. Structure integral transform versus Radon transform: A 2D mathematical tool for invariant shape recognition. IEEE Trans. on Image Processing, 2016, 25(12): 5635-5648.
[doi:10.1109/TIP.2016.2609816] |
| [6] |
Zhao C, Chan SSF, Cham WK, Chu LM. Plant identification using leaf shapes—A pattern counting approach. Pattern Recognition, 2015, 48(10): 3203-3215.
[doi:10.1016/j.patcog.2015.04.004] |
| [7] |
Wang B. Shape recognition using unordered point-set description and matching of object contour. Ruan Jian Xue Bao/Journal of Software, 2016, 27(12): 3131-3142(in Chinese with English abstract).
http://www.jos.org.cn/1000-9825/5101.htm [doi:10.13328/j.cnki.jos.005101] |
| [8] |
Belongie S, Malik J, Puzicha J. Shape matching and object recognition using shape contexts. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2002, 24(4): 509-522.
[doi:10.1109/34.993558] |
| [9] |
Ling HB, Jacobs DW. Shape classification using the inner-distance. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2007, 29(2): 286-299.
[doi:10.1109/TPAMI.2007.41] |
| [10] |
Belhumeur PN, Chen D, Feiner S, Jacobs DW, Kress WJ, Ling H, Lopez I, Ramamoorthi R, Sheorey S, White S, Zhang L. Searching the world's herbaria: A system for visual identification of plant species. In: Proc. of the European Conf. on Computer Vision. 2008. 116-129.
|
| [11] |
Backes AR, Casanova D, Bruno OM. A complex network-based approach for boundary shape analysis. Pattern Recognition, 2009, 42(1): 54-67.
[doi:10.1016/j.patcog.2008.07.006] |
| [12] |
Mokhtarian F, Mackworth AK. A theory of multi-scale, curvature-based shape representation for planar curves. IEEE Trans. on Pattern Analysis and Machine Intelligence, 1992, 14(8): 789-805.
[doi:10.1109/34.149591] |
| [13] |
Mokhtarian F, Abbasi S. Matching shapes with self-intersections: Application to leaf classification. IEEE Trans. on Image Processing, 2004, 13(5): 653-661.
[doi:10.1109/TIP.2004.826126] |
| [14] |
Manay S, Cremers D, Hong BW, Yezzi AJ, Soatto S. Integral invariants for shape matching. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2006, 28(10): 1602-1618.
[doi:10.1109/TPAMI.2006.208] |
| [15] |
Kumar N, Belhumeur PN, Biswas A, Jacobs DW, Kress WJ, Lopez IC, Soares JVB. Leafsnap: A computer vision system for automatic plant species identification. In: Proc. of the European Conf. on Computer Vision. 2012. 502-516.
|
| [16] |
Hu R, Jia W, Ling H, Huang D. Multiscale distance matrix for fast plant leaf recognition. IEEE Trans. on Image Processing, 2012, 21(11): 4667-4672.
[doi:10.1109/TIP.2012.2207391] |
| [17] |
Wang B, Gao Y. Hierarchical string cuts: A translation, rotation, scale and mirror invariant descriptor for fast shape retrieval. IEEE Trans. on Image Processing, 2014, 23(9): 4101-4111.
[doi:10.1109/TIP.2014.2343457] |
| [18] |
Sivic J, Zisserman A. Video google: A text retrieval approach to object matching in videos. In: Proc. of the 9th IEEE Int'l Conf. on Computer Vision. 2003. 1470-1477.
|
| [19] |
Csurka G, Dance C, Fan L, Willamowski J, Bray C. Visual categorization with bags of keypoints. In: Proc. of the Workshop on Statistical Learning in Computer Vision (ECCV 2004). 2004. 59-74.
|
| [20] |
Wang X, Feng B, Bai X, Liu W, Latecki LJ. Bag of contour fragments for robust shape classification. Pattern Recognition, 2014, 47(6): 2116-2125.
[doi:10.1016/j.patcog.2013.12.008] |
| [21] |
Wright J, Ma Y, Mairal J, Sapiro G, Huang TS, Yan S. Sparse representation for computer vision and pattern recognition. Proc. of the IEEE, 2010, 98(6): 1031-1044.
[doi:10.1109/JPROC.2010.2044470] |
| [22] |
Zeng S, Zhang B, Du Y. Joint distances by sparse representation and locality-constrained dictionary learning for robust leaf recognition. Computers and Electronics in Agriculture, 2017, 142: 563-571.
[doi:10.1016/j.compag.2017.11.013] |
| [23] |
Li Z, Tang J. Unsupervised feature selection via nonnegative spectral analysis and redundancy control. IEEE Trans. on Image Processing, 2015, 24(12): 5343-5355.
[doi:10.1109/TIP.2015.2479560] |
| [24] |
Lee SH, Chan CS, Mayo SJ, Remagnino P. How deep learning extracts and learns leaf features for plant classification. Pattern Recognition, 2017, 71: 1-13.
[doi:10.1016/j.patcog.2017.05.015] |
| [25] |
Xu C, Liu J, Tang X. 2D shape matching by contour flexibility. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2009, 31(1): 180-186.
[doi:10.1109/TPAMI.2008.199] |
| [26] |
Gope C, Kehtarnavaz N. Affine invariant comparison of point-sets using convex hulls and Hausdorff distances. Pattern Recognition, 2007, 40(1): 309-320.
[doi:10.1016/j.patcog.2006.04.026] |
| [27] |
Novotný P, Suk T. Leaf recognition of woody species in Central Europe. Biosystems Engineering, 2013, 115(4): 444-452.
[doi:10.1016/j.biosystemseng.2013.04.007] |
| [28] |
Sebastian TB, Klein PN, Kimia BB. Recognition of shapes by editing their shock graphs. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2004, 26(5): 550-571.
[doi:10.1109/TPAMI.2004.1273924] |
| [29] |
Wang J, Bai X, You X, Liu W, Latecki LJ. Shape matching and classification using height functions. Pattern Recognition Letters, 2012, 33(2): 134-143.
[doi:10.1016/j.patrec.2011.09.042] |
| [30] |
Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition. In: Proc. of the Int'l Conf. on Learning Representations (ICLR 2015). 2015. 1-14.
|
| [31] |
Zagoruyko S, Komodakis N. Wide residual networks. In: Proc. of the British Machine Vision Conf. 2016. 87.1-87.12.
|
| [32] |
Manning CD, Raghavan P, Schuetze H. Introduction to Information Retrieval. Cambridge University Press, 2008.
|
| [7] |
王斌. 用于形状识别的目标轮廓无序点集描述与匹配. 软件学报, 2016, 27(12): 3131-3142.
http://www.jos.org.cn/1000-9825/5101.htm [doi:10.13328/j.cnki.jos.005101] |
 2021, Vol. 32
2021, Vol. 32





