作为一种丰富的信息描述手段, 可视化语言(可视化图)是软件系统概念设计阶段中重要的人机交互工具, 例如数据库系统概念设计阶段的E-R(entity-relationship)图、面向对象系统中的UML(unified modeling language)图以及描述离散并行系统的Petri网.可视化语言研究的重点之一是如何使用有效而又规范的方式去描述各种不同类型的可视化语言.一部分研究者尝试使用一维字符文法描述可视化语言, 然而, 由于图的二维性以及非线性特点, 字符文法在描述可视化语言时有着表达能力不足以及直观性较差等问题.基于形式语言理论, 图文法是一种使用产生式(图重写规则)进行图语言定义与分析的二维化形式化工具.使用图文法对各种可视化语言语法结构的描述、操纵和分析, 具有直观明了和简便的优点.至今, 图文法已被广泛地应用于各种可视化语言的配置与分析中, 例如图语言定义与转换^[1]、图模型的动态分析^[2].不仅如此, 图文法还被广泛地应用于软件系统建模^{[3, 4]}、信息可视化^[5]、模式识别^[6−8]等领域.

作为二维或三维空间上最重要的特征之一, 空间语义信息在可视化语言的空间拓扑结构描述以及空间知识呈现上是不可或缺的关键因素之一.然而, 大多数图文法在面向空间语义处理需求时存在诸多困难之处.Stiny和Gips从描述空间元素形状的角度出发, 提出了形状文法SG(shape grammar)^{[9, 10]}.SG将形状定义为一系列空间元素的有限排列, 例如线段、点、矩形.SG的文法直观易懂, 可以被广泛地应用于建筑图像分析^[11]、绘图设计^[12]等领域.根据事先定义的规则, SG可以通过迭代地使用形状替换操作来生成各种各样的设计.然而, 由于只支持单方向的工作流, SG更侧重于完成不同类型图形的生成绘制工作, 而在图形分析处理能力上有所欠缺.Kong等人^{[13, 14]}在上下文相关图文法RGG(reserved graph grammar)^[15]形式框架中加入了空间信息处理机制, 提出了一种空间图文法——SGG(spatial graph grammar).SGG对空间语义信息采用定性研究方法进行描述, 包括6种拓扑关系、4种方向关系、顺序距离关系以及7种对齐关系.基于定性分析方法, SGG可以较为直观灵活地分析各种可视化语言的语法与语义结构, 在网页描述及模式验证^{[16, 17]}领域取得了较好的应用效果.然而, SGG也有存在一些不足之处: 首先, 由于对空间语义信息缺少定量描述能力, SGG在对空间关系进行配置时缺乏相应的精准性; 其次, SGG中使用额外的语义函数描述空间语义关系, 并通过执行操作代码实现语义变换, 较大程度地增加了SGG在实际应用中的复杂性.针对SG与SGG文法框架的局限性, 本文作者在前期研究中提出了一种坐标图文法框架——CGG(coordinate graph grammar)^[18], 将空间语义信息的定量和定性描述机制整合在一个理论框架内, 并利用图形元素之间的坐标关系设计了相对低时间开销的图柄查找算法, 为空间语义信息提供了相对灵活的配置方案.表 1给出了CGG与SG、SGG这两种具有代表性的空间文法框架的对比, CGG在保持SG和SGG优点的同时弥补了两者的不足, 为空间语义配置提供了一个更全面的形式化框架.目前, CGG已被应用在UML类图定义与布局^[19]、流程图生成与检测^[18]等实际案例中.然而, CGG是在EGG(edge based graph grammar)^[20]的理论框架的基础上加入空间语义机制而构建的图文法形式框架, 因此, EGG的部分缺陷延伸到了CGG中: 首先, CGG中悬边图的概念不符合图论中点边图的定义, 使得图柄结构的规范性有所欠缺; 其次, 在CGG的归约操作中, 悬边的匹配需要考虑图柄排列问题, 导致大量冗余图柄的出现, 在一定程度上增加了归约执行步数, 也导致大量无效归约的产生; 最后, CGG产生式中使用悬边描述上下文信息, 通过减少上下文信息的匹配提高文法的抽象程度, 却在某种程度上影响了文法的直观性以及表达能力.针对上述问题, 本文在前期研究的基础上, 通过定义虚结点的概念, 构建一个新的空间图文法框架vCGG(virtual node based coordinate graph grammar).该框架在文法中保留上下文结点的同时, 维持CGG产生式的抽象能力, 从而为图的空间语义提供更加直观而全面的形式化描述与分析手段.

本文第1节介绍CGG的理论框架.第2节在CGG基础上构建一个新的空间图文法框架vCGG, 包括框架的基本概念与文法操作.第3节对vCGG与几种具有代表性的空间图文法进行对比分析.第4节给出总结及展望.

1 CGG形式框架 1.1 基本概念

CGG是在上下文相关图文法EGG中引入空间语义机制扩展而来的空间图文法形式框架, 通过在传统连续坐标的基础上定义离散坐标的概念, 使用两个子框架cCGG(continuous coordinate graph grammar)和dCGG (discrete coordinate graph grammar), 为分别空间语义提供定量与定性描述粒度.以下给出CGG中的基本概念.

定义1.1. G=(N, E)是一个定义在标号集L上的空间语义图, 当且仅当:

● N是一个结点集, 并且可以进一步被分为两个子集合: 终结点集N_T和非终结点集N_NT;

● E⊆N×N是一个有向边集.

为了方便语法语义操作, CGG定义了以下几个函数.

● f_NL: N→L是一个从结点n∈N到标号l∈L的映射, 即f_NL(n)=n.l;

● f_NC: N→R×R是一个从结点n∈N到坐标c∈R×R的映射;

● ${f_{E{N_s}}}:E \to N$是一个从有向边e∈E到它的起始结点的映射;

● ${f_{E{N_e}}}:E \to N$是一个从有向边e∈E到它的结束结点的映射.

定义1.2. 给定一个空间语义图G, 结点n∈G.N的离散坐标是(r_x, r_y), 当且仅当:

● r_x和r_y分别是f_NC(n).x和f_NC(n).y在G.N中所有结点坐标值中的反向排名数值.

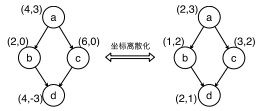
对于一个给定的图, 结点的离散坐标抽象自连续坐标, 表示结点的横坐标与纵坐标在当前图所有结点中的反向排名, 反映了该结点在图中的相对空间位置.例如, 图 1是一个空间图连续坐标的离散化过程, 结点a横坐标与纵坐标在图中所有的结点中反向排名为2, 3, 因此, 结点a在当前图中的离散坐标为(2, 3).

定义1.3. 图G与图Q是同构关系, 记作G≈Q, 其中, G和Q之间存在两个双射: f_NN: G.N↔Q.N和f_EE: G.E↔Q.E, 并满足以下条件.

● $\forall n(((n \in G.N) \vee (n \in Q.N)) \Rightarrow ({f_{NL}}(n) = {f'_{NL}}({f_{NN}}(n))))$, 其中, f_NL和${f'_{NL}}$分别是G和Q的结点标号映射;

● $ \forall e(((e \in G.E) \vee (e \in Q.E)) \Rightarrow ({f_{NN}}({f_{E{N_s}}}(e)) = {f_{E{N_s}}}({f_{EE}}(e))) \wedge ({f_{NN}}({f_{E{N_e}}}(e)) = {f_{E{N_e}}}({f_{EE}}(e)))) $.

满足同构关系的两个图有着一一对应的结点和边, 其中, 对应结点拥有相同的标号, 并且对应边的起始结点和结束结点也需符合该对应关系.

定义1.4. 图Q是一个包含悬边的图$\bar G$的核图, 记作$Q = Cor(\bar G)$, 当且仅当:

$ (Q.N = \bar G.N) \wedge (Q.E = (\bar G.\bar E - \bar G.\dot E)) \wedge (Q.L = \bar G.L). $

定义1.5. 如果图Q是一个给定主图G的子图并可能带有悬边, 并且图${\bar G_{L|R}}$是一个产生式的左图或右图, 图Q是图${\bar G_{L|R}}$在主图G中的图柄, 记作$Q \in Redex(G,{\bar G_{L|R}})$, 当且仅当: 存在两个双射: ${f_{NN}}:Q.N \leftrightarrow {\bar G_{L|R}}.N$和f_EE: $Q.E \leftrightarrow {\bar G_{L|R}}.E$, 并满足以下条件.

● $Cor(Q) \approx Cor({\bar G_{L|R}})$;

● $\forall n(n \in \bar Q.N \Rightarrow ({d_s}(n) = {d_s}({f_{NN}}(n))) \wedge ({d_e}(n) = {d_e}({f_{NN}}(n))))$;

● cCGG: $\forall {n_1},{n_2}({n_1},{n_2} \in Q.N \Rightarrow ({f_{NC}}({n_1}) - {f_{NC}}({n_2}) = {f'_{NC}}({f_{NN}}({n_1})) - {f'_{NC}}({f_{NN}}({n_2}))))$, 其中, f_NC和${f'_{NC}}$分别是Q和${\bar G_{L|R}}$的结点坐标映射;

● dCGG: ∀n(n∈Q.N⇒(n.c_d=(f_NN(n).c_d))), 其中, c_d是Q或${\bar G_{L|R}}$中结点的离散坐标.

在CGG中, 图柄不仅要求与某个产生式图形成同构关系, 还需满足空间上的语义匹配要求.根据不同的粒度描述选择, 子框架cCGG要求产生式图${\bar G_{L|R}}$中任意两个结点和它们在图柄Q中对应的结点具有完全相等的坐标差值; 而dCGG要求产生式图${\bar G_{L|R}}$和图柄Q具有等价的空间拓扑结构, 即${\bar G_{L|R}}$中任意一个结点和它在图柄Q中对应的结点具有完全相等的离散坐标值.

在图文法的推导或归约工作流中, 在根据一个产生式图找到其在主图中的图柄后, 便可以对图柄执行图转换操作.根据不同的配置粒度, cCGG和dCGG中图转换操作的具体步骤如下.

1) 根据当前产生式生成一个产生式实例;

2) 平移产生式实例的右图或左图${\bar G_{R|L}}.$

➢ cCGG: 将图柄中的任意结点n与其在产生式图${\bar G_{L|R}}$中的对应节点n′的坐标差值, 即n.c−n′.c, 作为偏移量平移产生式的另一端${\bar G_{R|L}};$

➢ dCGG: 首先, 在产生式图${\bar G_{L|R}}$中选择一个具有最大“Y”值的结点n′, 若存在多个(大于1)这样的结点, 则从中选择具有最小“X”值的结点; 其次, 将图柄中的对应结点n与n′的坐标差值n.c−n′.c作为偏移量平移另一个产生式图${\bar G_{R|L}};$

3) 从主图中删除图柄;

4) 将产生式图${\bar G_{R|L}}$嵌入到主图中.

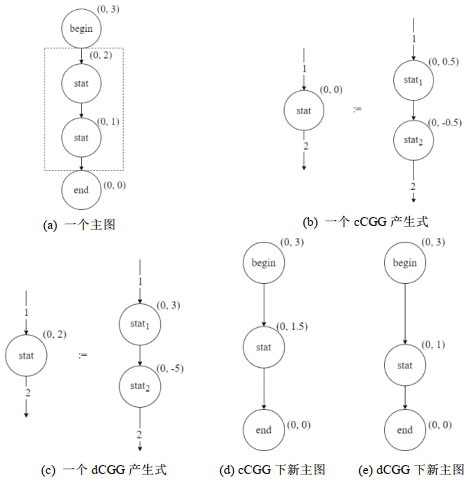
图 2是一个CGG中R-application的例子, 其中, 图 2(a)是一个给定主图, 图 2(b)和图 2(c)分别是一个cCGG产生式和dCGG产生式.对于cCGG产生式, 产生式实例的左图使用偏移量(0, 1.5)进行平移, 该偏移量是图 2(a)中虚线框内所示图柄与产生式右图之间匹配结点的坐标差值.而对于dCGG产生式, 首先在产生式右图中选择具有最大“Y”坐标值的结点“stat₁”, 然后将图柄中的对应结点与结点“stat₁”的坐标差值(−1, 0)作为偏移量, 平移产生式左图.在该例中, 使用cCGG产生式和dCGG产生式对图柄进行R-application操作, 得到的是两个不同的主图, 如图 2(d)、图 2(e)所示.

1.2 框架缺陷

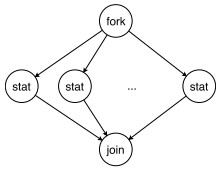
由于延续了EGG的悬边机制, CGG存在一个较为明显的表达能力上的缺陷——L_cf图语言问题^[21].如图 3所示, 图语言L_cf是由一对“fork”, “join”结点以及它们之间的任意数量(不小于2)“stat”分支组成的一类流程图.对于这一类图语言, 无法通过有限数量的EGG或CGG产生式描述所有可能情形下的L_cf图.其原因在于: 如果要描述任意一个L_cf, 由于“stat”分支的数量是未知的, 无法在产生式设计阶段穷举所有分支, 从而无法在产生式中确定“fork”与“join”结点所连接的悬边数量.L_cf图语言问题可以通过定义额外的通配悬边加以解决, 然而通配悬边的处理在一定程度上增加了产生式以及文法操作的复杂性.相比之下, 图文法LGG和RGG则不存在这个问题.在产生式设计阶段, LGG可以将出入边数量未知的结点(例如“fork”和“join”结点)作为上下文结点, 在匹配时不需要考虑上下文结点的出入度; RGG使用双层结构结点中标记的顶点来关联上下文, 在匹配时不需要考虑顶点所连接边的数量.

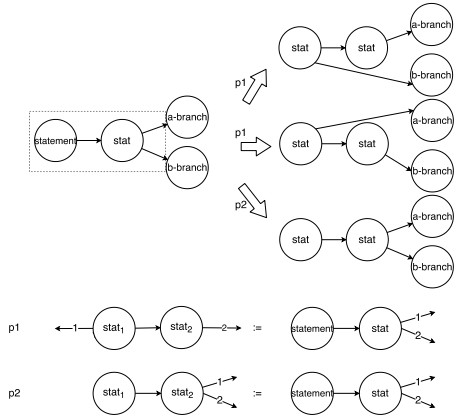
悬边机制带来的另一个问题是悬边映射问题.在EGG和CGG的工作流中, 当一个主图子图与产生式图符合图柄匹配条件时, 若产生式图中存在一个结点连接了两条及两条以上同方向的悬边, 需根据这些悬边在主图中不同映射情况生成多个图柄进行处理^[20].如图 4所示, 左侧主图虚线框内的子图与产生式p1与p2的右图之间均满足图柄匹配条件.由于产生式p1的右图结点“stat”连接了两条同方向的悬边“1”、悬边“2”, 两条悬边与主图中对应结点“stat”所连接的边(stat, a-branch), (stat, b-branch)之间存在两种双射, 而在不同双射情况下进行R- application会产生两种具有不同结构的主图, 因此, 两种双射情况下的图柄应当被视为不同的图柄.这种规定可以保证图转换结果的唯一性, 然而该规定在一些场景下并不是必要的.例如: 对于图 4中的产生式p2, 在任意一种双射情况下对主图进行R-application所产生的新主图均具有相同的结构.原因在于: 悬边“1”、悬边“2”在产生式p2的左图中只与一个结点“stat₂”相连接, 在进行子图替换的过程中, 主图的余图只能与该结点进行连接, 因而不会出现两种图转换结果.在这种情况下, 如果按照上述规定进行归约, 则容易因图柄集规模扩大而导致多余回溯的出现, 产生不必要的分析时间开销.

2 vCGG形式框架 2.1 基本概念

针对空间图文法存在的问题, 本章在继承CGG形式框架空间语义机制的前提下构建新的空间图文法框架vCGG, 该框架引入虚结点作为上下文结点, 描述图柄与产生式之间语法结构与空间语义上的关系, 在保留文法抽象性的同时, 增加文法的表达能力与分析效率.由于CGG使用两个子框架dCGG与cCGG分别处理定性与定量空间语义关系, vCGG根据空间语义的不同粒度描述分为vdCGG(virtual-node based discrete coordinate graph grammar)与vcCGG(virtual-node based continuous coordinate graph grammar), 以下是vCGG形式框架中基本概念的定义.

定义2.1. G=(N, E)是一个定义在标号集L上的空间语义图, 当且仅当:

● L=L_v∪L_r, L_v∩L_r=Ø, 其中, L_v是虚结点的标号集, L_r是实结点的标号集;

● L_r=L_T∪L_NT, L_T∩L_NT=Ø, 其中, L_T是终结点的标号集, L_NT是非终结点的标号集;

● N是一个结点集并且可以被分为两个子集合: 虚结点集N_v、实结点集N_r, 其中, 实结点集N_r可以进一步分为终结点集N_T和非终结点集N_NT;

● E⊆N×N是一个有向边集.

为了方便于语法语义操作, CGG定义了以下几个函数.

● f_NL: N→L是一个从结点n∈N到标号l∈L的映射, 即f_NL(n)=n.l;

● f_NC: N→R×R是一个从结点n∈N到坐标c∈R×R的映射;

● ${f_{E{N_s}}}:E \to N$是一个从有向边e∈E到它的起始结点的映射;

● ${f_{E{N_e}}}:E \to N$是一个从有向边e∈E到它的结束结点的映射.

在vCGG中, 图中包含的结点根据分配的标号被分成了两类: 虚结点和实结点, 其中, 实结点可以进一步地分为终结点与非终结点.实结点的标号集定义与CGG相同, 而虚结点的标号主要用于区分不同虚结点标记, 不包含其他语义信息, 因此, 主图中虚结点在通常情况下其标号集为空, 即主图的所有结点都是实结点.虚结点的主要作用是描述主图与产生式的语法结构与空间语义关系, 下面给出vCGG产生式的定义.

定义2.2. 产生式是两个图G_L和G_R组成的形如G_L: =G_R的表达式, 在G_L和G_R之间存在一个双射f_NN: G_L.N_v↔ G_R.N_v, 并满足以下条件.

● $\forall n((n \in {G_L}.{N_v}) \Rightarrow ({f_{NC}}(n) = {f'_{NC}}({f_{NN}}(n))))$, 其中, f_NC和${f'_{NC}}$分别是G_L和G_R的结点坐标映射;

● $\forall n((n \in {G_L}.{N_v}) \Rightarrow ({f_{NL}}(n) = {f'_{NL}}({f_{NN}}(n))))$, 其中, f_NL和${f'_{NL}}$分别是G_L和G_R的结点标号映射;

● ∀n₁, n₂((n₁, n₂∈G_L.N_v)∧(n₁≠n₂)⇒(f_NL(n₁)≠f_NL(n₂)));

● $\forall {n_1},{n_2}(({n_1},{n_2} \in {G_R}.{N_v}) \wedge ({n_1} \ne {n_2}) \Rightarrow ({f'_{NL}}({n_1}) \ne {f'_{NL}}({n_2})))$.

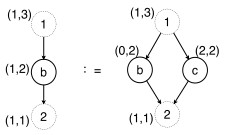
vCGG将虚结点引入产生式结构中.在一个产生式图中, 虚结点表示上下文结点, 而实结点代表非上下文结点, 也可称为产生式内部结点.为了图转换操作的可执行性, vCGG规定: 同一个产生式两端的虚结点集之间需存在一个双射, 并且对应的结点拥有相等的标号与坐标.此外, 为了图嵌入过程中不产生歧义, 同一个图中的每一个虚结点具有唯一的标号, 可以用唯一的整数表示.例如, 图 5是一个合法的vCGG产生式, 其中, 虚线圆框代表虚结点, 实线圆框代表实结点.

由图 5可见: 产生式左图与右图之间存在一个双射, 并且对应结点具有相同的标号“1”、标号“2”以及相等的坐标(1, 3), (1, 1).

定义2.3. 图G与图Q是同构关系, 记作G≈Q, 其中, G和Q之间存在两个双射: f_NN: G.N↔Q.N和f_EE: G.E↔Q.E, 并满足以下条件.

● $\forall n((n \in G.N) \vee (n \in Q.N) \Rightarrow ({f_{NL}}(n) \in {L_v}) \vee ({f'_{NL}}({f_{NN}}(n)) \in {L_v}) \vee ({f_{NL}}(n) = {f'_{NL}}({f_{NN}}(n))))$, 其中, f_NL和${f'_{NL}}$分别是G和Q的结点标号映射;

● $\forall e((e \in G.E) \vee (e \in Q.E) \Rightarrow ({f_{NN}}({f_{E{N_s}}}(e)) = {f_{E{N_s}}}({f_{EE}}(e))) \wedge ({f_{NN}}({f_{E{N_e}}}(e)) = {f_{E{N_e}}}({f_{EE}}(e))))$.

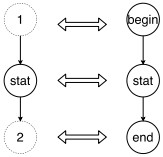
在判定一对图是否满足同构条件时, 虚结点比实结点具有更高的抽象程度, 可以匹配任意标号的结点.图 6是一个vCGG中图同构的例子, 其中, 所有结点和边在满足双射关系的.其中, 实结点“stat”和对应结点必须具有相同的标号, 而虚结点“1”、虚结点“2”可以匹配任何标号的结点(图 6中为“begin”“end”).

定义2.4. 如果图Q是一个给定主图G的子图, 图G_L|R是一个产生式的左图或右图, 图Q是图G_L|R在主图G中的图柄, 记作Q∈Redex(G, G_L|R), 当且仅当: 存在两个双射: f_NN: Q.N↔G_L|R.N和f_EE: Q.E↔G_L|R.E, 并满足以下条件.

(1) vcCGG

● Q≈G_L|R;

● $\forall n((n \in Q.N \wedge (({f'_{NL}}({f_{NN}}(n)) \in {L_r})) \Rightarrow ({d_s}(n) = {d_s}({f_{NN}}(n))) \wedge ({d_e}(n) = {d_e}({f_{NN}}(n))))$, 其中, d_e(n)和d_s(n)是结点n在主图中的出入度;

● $\forall {n_1},{n_2}(({n_1},{n_2} \in Q.N) \Rightarrow ({f_{NC}}({n_1}) - {f_{NC}}({n_2}) = {f'_{NC}}({f_{NN}}({n_1})) - {f'_{NC}}({f_{NN}}({n_2}))))$, 其中, f_NC和${f'_{NC}}$分别是Q和G_L|R的结点坐标映射.

(2) vdCGG

● Q≈G_L|R;

● $\forall n((n \in Q.N \wedge (({f'_{NL}}({f_{NN}}(n)) \in {L_r})) \Rightarrow ({d_s}(n) = {d_s}({f_{NN}}(n))) \wedge ({d_e}(n) = {d_e}({f_{NN}}(n))))$, 其中, d_e(n)和d_s(n)是结点n在主图中的出入度;

● ∀n((n∈Q.N)⇒(n.c_d=(f_NN(n)).c_d))), 其中, c_d是Q或G_L|R中结点的离散坐标;

● $\forall {n_1},{n_2}(({n_1},{n_2} \in Q.N) \wedge ({f'_{NL}}({f_{NN}}({n_1})) \in {L_v}) \wedge ({f'_{NL}}({f_{NN}}({n_2})) \in {L_v}) \Rightarrow ({f_{NC}}({n_1}) - {f_{NC}}({n_2}) = {f'_{NC}}({f_{NN}}({n_1})) - {f'_{NC}}$$({f_{NN}}({n_2})))$.

其中, f_NL和${f'_{NL}}$是Q和G_L|R的结点标号映射, f_NC和${f'_{NC}}$分别是Q和G_L|R的结点坐标映射.

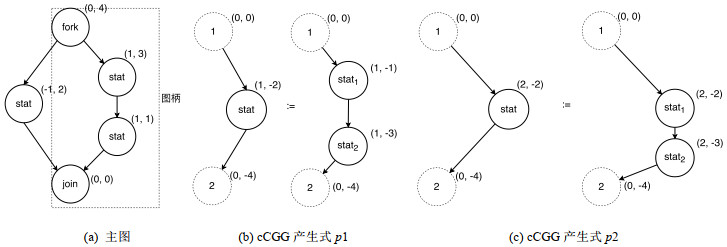
基于不同的空间语义描述粒度, vCGG两个子框架vcCGG与vdCGG的图柄定义有所不同.在满足同构关系的前提下, vcCGG要求图柄和产生式图需要满足坐标关系的完全匹配, 产生式图中任意两个结点与它们在主图中对应结点具有相等的坐标差, 即产生式图通过平移可以与图柄完全重合.与vcCGG相比, vdCGG空间语义匹配条件按照虚结点和实结点分为两个层次: 在第1层, 图柄和产生式图的对应结点需要在各自空间内部具有相等的离散坐标; 在第2层, 虚节点之间的定量坐标关系需要和对应主图结点完全一致, 即所有虚结点可以同时通过平移与其在图柄中的对应结点完全重合.匹配要求的划分使vCGG既能对产生式内部结点提供定性与定量的拓扑关系描述, 也能维持上下文结点的一致性.例如: 图 7(a)是一个主图, 若根据图 7(b)中产生式右图在主图中查找图柄时, 在vcCGG和vdCGG中的任何一个子框架下, 该产生式右图都符合图柄的匹配条件; 而当在主图中查找图 7(b)中产生式右图的图柄时, 在vcCGG框架下产生式右图与主图的任何一个子图都不符合坐标匹配条件, 而在vdCGG框架下则可以成功查找到所需图柄.此外, vCGG要求图柄中实结点在主图中的出入度与产生式图中对应结点完全相等, 保证了图柄中所有与产生式图中实结点对应的结点在主图中只能与虚结点对应的结点相连接, 在图转换过程中避免了悬边的出现.

2.2 文法操作

图文法的主要工作流是图推导与归约, 分别面向实际应用中图的生成与分析需求.推导与归约工作流的基本构成要素是图转换操作.图转换操作根据其执行方向可以分为L-application与R-application, 其中, L- application是指用产生式右图替换左图在主图中图柄的操作, 而R-application用产生式左图替换右图在主图中图柄.L/R application中的一个重要问题是如何避免转换后的新主图中产生悬边, 即嵌入问题.在vCGG中, 由于在产生式使用虚结点作为上下文结点, 可以使用粘合的方式解决嵌入问题.根据不同的配置粒度要求, vcCGG和vdCGG中L/R application的具体步骤如下.

1) 根据当前产生式生成一个产生式实例;

2) 平移产生式实例的右图或左图G_R|L.

➢ vcCGG: 将图柄中的任意结点n与其在产生式图G_L|R中的对应节点n′的坐标差值, 即n.c−n′.c, 作为偏移量平移产生式的另一端G_R|L;

➢ vdCGG: 首先, 在产生式图G_L|R中选择任意一个虚结点n′, 将图柄中的对应结点n与n′的坐标差值n.c−n′.c作为偏移量平移另一个产生式图G_R|L;

3) 从主图中删除图柄中所有的边以及与G_L|R中实结点匹配的结点;

4) 按照产生式图G_L|R的虚节点与图柄结点的映射关系, 粘合产生式图G_R|L的虚结点与图柄中对应结点, 并在主图中去除该虚标号.

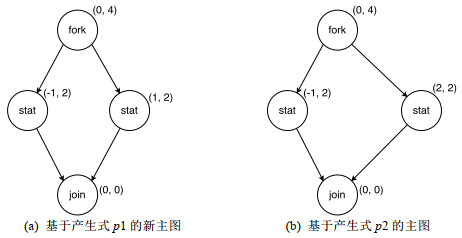
vCGG图转换的操作继承了CGG中的坐标映射机制, 即产生式局部坐标与主图全局坐标的映射关系, 区别在于: vdCGG基于虚结点而计算获得坐标偏移量, 而dCGG的偏移量是基于最大“Y”值的结点而计算得出.相比之下, vdCGG偏移量的可解释性更好, 产生式设计人员的学习曲线较为平缓.图 8描述了使用图 7中的产生式p1和p2对图 7(a)中的主图分别进行R-application生成的新主图, 其中, 图 8(a)是使用图 7(a)中产生式p1在vcCGG框架下生成的新主图, 图 8(b)是使用产生式p2按照vdCGG的R-application步骤生成的主图.

2.3 vCGG及其语言定义

定义2.5. vCGG是一个四元组(λ, L, P, S), 其中,

● λ是一个初始图;

● L=L_v∪L_r, L_v∩L_r=Ø, 其中, L_v是虚结点的标号集, L_r是实结点的标号集;

● L_r=L_T∪L_NT, L_T∩L_NT=Ø, 其中, L_T是终结点的标号集, L_NT是非终结点的标号集;

● P是一个产生式集;

● S是一个由若干正实数组成的标尺集, 并且满足关系: S⊆R+.

为了避免产生式的冗余, vCGG的形式化定义中继承了CGG的标尺集概念.类似于地图标尺, 标尺集中的每一个正实数代表着主图对产生式的坐标比例.标尺的引入, 可以有效地减少产生式的数量, 尤其是那些结构完全相同而互相之间坐标成比例关系的产生式.每个产生式集P中的产生式都可以通过坐标与标尺的相乘得到多个实际使用的产生式, 因此, 标尺集所包含正实数的数量对一个文法的实际表达能力有着重要的影响.

定义2.6. 对于vCGG的任意一个文法vcgg, 其语言Γ(vcgg)是一个由空间语义图组成的集合:

$ \mathit{\Gamma }(vcgg)={G(λ→*G)∧f_{NL}(G.N)∈L_{T}}. $

图文法的语言是由初始图经过推导操作生成的只含有终结点的图的集合.对一个只含有终结点的图进行归约操作的过程, 可以判断该图是否属于相应文法所定义的语言.vCGG的推导工作流生成的是一个包含空间语义配置的图, 而归约工作流可以在判断给定图的结构语法的合法性的同时, 分析该图的空间语义模型.

3 与已有文法的对比

本节对新构建的vCGG框架与几种具有代表性的框架SGG、SG、CGG进行对比, 其中, SGG对空间语义采用定性描述, SG根据文法定义的定量空间关系绘制图形, CGG使用离散坐标和连续坐标为空间语义提供基于不同粒度的配置.为了获得全面而系统的比较结论, 本节从形式化框架、文法表达能力、分析效率、以及文法应用这4个维度对这几种框架进行对比分析.

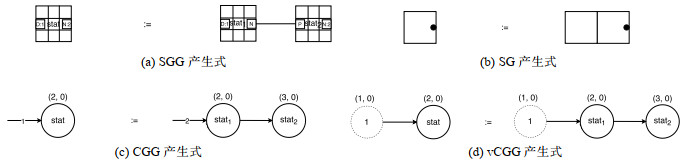
3.1 形式化框架

直观性是衡量一个图文法形式框架的关键特性之一, 而上下文深度是评价文法框架直观性的一个重要依据.上下文深度是指产生式图中内部结点到上下文结点的最短路径长度, 具体值等于最短路径中结点(不包含起始结点)和边数量之和的二分之一.上下文深度大于等于1的文法称为显式文法, 而小于1的文法称为隐式文法.一般而言, 显式文法的直观性高于隐式文法, 而显式文法的不足在于上下文结点描述的复杂性, 在很多应用场景下较难使用有限的上下文结点描述所有可能出现的上下文信息.例如: LGG使用通配符描述上下文信息, 当通配符数量较大时, 产生式构造变得过于复杂而难以设计.对几种框架的上下文深度进行对比, 如图 9所示: SGG将上下文信息以顶点形式内嵌在结点的双层结构中, 上下文深度为0;CGG继承了EGG的悬边机制, 采用悬边表示上下文连接, 因此上下文深度为0.5;SG在形式上没有对上下文信息进行描述, 上下文深度为空; vCGG在产生式中引入了虚结点, 上下文深度为1, 并且虚结点在图柄查找过程中不需要匹配其标号语义信息, 因此不需要考虑虚结点除空间坐标之外的语义信息, 相比LGG具有更高的抽象性, 产生式结构也更为简洁而易于设计.此外, 与前身CGG相比, 由于不再需要定义悬边图作为图柄, vCGG中图的形式与定义更加符合图论的规范标准.

形式化框架比较的另一个重点是子图嵌入问题的解决方法, 大致可以分为两种: 一种是使用嵌入规则进行图转换操作, 具体方法是在主图中首先删除图柄, 之后根据嵌入规则将产生式图嵌入主图中; 另一种方法使用结点粘合的方式, 首先在主图中删除图柄中除了与上下文结点匹配的结点之外的部分, 再根据产生式两端上下文结点的双射关系进行结点粘合.总体而言: 嵌入规则方法的形式上更加灵活, 例如, 用户可以通过修改嵌入规则改变嵌入前边的方向; 粘合方法的规范性更好, 可以确保文法操作中不会出现悬边.相比之下, SG、SGG、CGG都是使用嵌入规则的方式进行子图嵌入操作, 而vCGG采用粘合方式将作为上下文结点的虚结点和其对应结点进行粘合并去除虚标号, 从而得到合法的新主图.

3.2 文法表达能力

图文法形式框架的表达能力指的是文法能够描述图语言的范围, 如何增强图文法的表达能力, 是该领域中的一个重要研究话题.与CGG相比, 对于图语言L_CF问题, 由于引入了虚结点机制, vCGG可以将第1.2节中图 3的结点“fork”, “join”放入产生式中作为虚结点, 直观而简洁地描述所有形如L_cf图语言的多分支结构图.从空间语义配置的全面性上对几种框架进行对比, vCGG对图语言空间语义的描述更加全面.vCGG在产生式中引入了虚结点作为上下文结点, 虚结点在图柄查找时不需考虑标号语义, 匹配的是虚结点与实结点之间的语法结构以及空间语义关系, 因此, vCGG不仅可以描述产生式非公共子图(不包含上下文结点的部分)的空间语义模型, 也可以通过上下文结点的空间语义描述非公共子图与主图之间的坐标方位关系.与之对比, SG、SGG与CGG的产生式只能描述非公共子图内部空间语义模型, 缺乏对图柄与主图之间空间语义关系的描述能力, 因此, 空间语义配置的全面性不如vCGG.

3.3 分析效率

在文法分析效率方面, 由于图语言结构的二维非线性特点, 文法分析过程中容易发生大量的回溯, 造成了分析算法的最坏时间开销通常为指数级.继承自RGG、SGG可以使用一个时间开销为多项式级的分析算法——SFPA算法(selection-free parsing algorithm)^[15].然而, SFPA算法对产生式提出了约束较高的选择无关条件作为归约前提, 导致SFPA的通用性有所不足.由于归约中回溯的不可避免性, 大多数图文法分析算法的设计目标是尽可能地降低图柄查找过程的时间开销.假设n是主图的结点数量, m是产生式右图的结点数量, n与m代表了主图与产生式的规模, 图文法的图柄查找时间开销的时间复杂度在通常情况下为$ {\rm{O }}(A_n^m)$, 即在规模为n的主图能够查找到规模为m的不同结点顺序子图的最多数量.引入了空间语义机制后, 由于产生式以及主图中的结点可以按照其空间拓扑关系进行排序, 利用该顺序指导子图匹配过程可以有效缩小图柄的查找空间, 从而减少时间开销.因此, SGG与CGG的图柄查找算法时间开销位于$ {\rm{ O }}(C_n^m)$^{[13, 18]}量级, 将传统图柄查找过程的排列问题转变成了典型的组合问题.继承自CGG、vCGG可以使用CGG的图柄查找算法, 通过对结点排序而缩小图柄的搜索空间, 并且由于图柄查找过程中不需要考虑悬边的映射问题, vCGG分析算法的实际时间开销小于CGG.

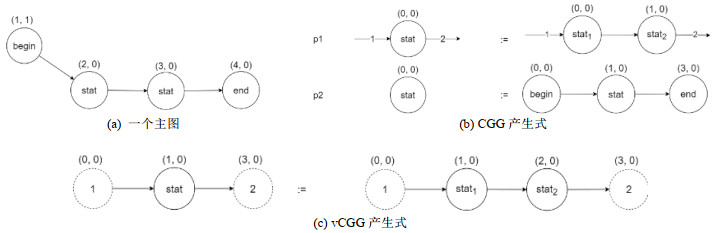
图文法分析性能的评价不仅体现在其时间开销上, 对非法语义关系与语法结构作出判断的及时性也是评价的一个重要依据.与SG、SGG、CGG相比, vCGG产生式增加了上下文与产生式非公共子图之间的空间关系约束, 因此在分析过程中可以更早地发现错误, 即时停机从而减少无效归约.例如, 图 10(a)是一个任意给定的主图, 不满足图 10(b)、图 10(c)中产生式对图形元素的空间语义约束.在归约时, 图 10(b)中CGG产生式需要根据产生式p1, p2对主图进行两次归约才可以判定出该语义错误, 而vCGG产生式只需要图 10(c)中的一个产生式进行一步归约便可判断出其空间语义关系的非法性, 在一定程度上减少了无效归约的数量.

3.4 文法应用

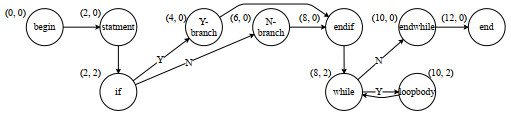
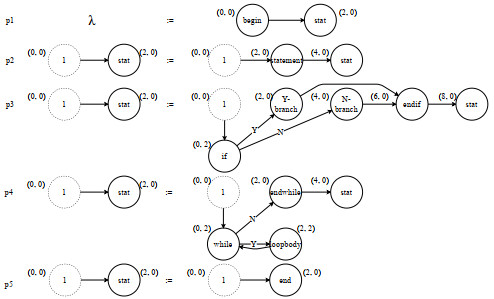
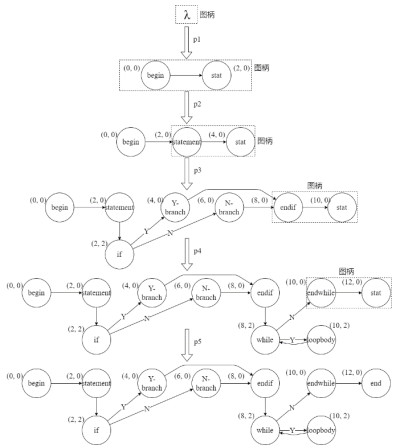
通过上述对比, vCGG不仅可以描述产生式图内部的空间语义模型, 也可以将虚结点作为上下文结点直观地描述产生式图内部与主图的坐标方位关系, 提供了相对更全面的空间语义配置能力.因此, 在空间图文法的实际应用中, vCGG可以处理一部分SG、SGG与CGG较难应对的实际应用问题.以图模型布局需求为例, 图 11是一个简单的程序流程图, 其布局要求为: 结点按从左到右的顺序排列, 每一个标号为“if”或“while”的结点需位于前一结点(设为n)的正下方, 而标号为“Y-branch”或“endwhile”的结点需位于结点n的正右方.基于虚结点对上下文空间语义的显式配置, 使用vCGG产生式可以较为容易地实现该布局要求.图 12是一组用于绘制流程图的vCGG产生式.而使用该组产生式进行推导操作即可绘制出满足上述布局要求的程序流程图, 如图 13所示.

相比之下, SG、SGG与CGG只能配置产生式图内部的空间语义模型而缺乏对产生式与上下文之间的空间语义关系的描述.在面对上述需求时, 最直接的方法是将vCGG产生式中的虚结点(即上下文结点)引入产生式中作为普通实结点.例如, 图 14是一个满足上述关于“if”结点布局要求的CGG产生式.然而, 该方法存在着较大的弊端: 首先, 将虚结点引入产生式作为普通实结点需要穷举该结点允许接受的标号(如“statement”“endif”), 而每种标号都对应着一个产生式, 造成了产生式规模与数量的增长, 尤其在需要引入多个虚结点作为实结点时, 产生式的数量随之呈指数增长; 其次, 实结点的增加在一定程度上影响了产生式图作为一个图形单元的逻辑独立性, 例如, 图 14中产生式中出现了不属于“if”选择结构的实结点“statement”; 最后, 在产生式中引入普通实结点还需考虑它们的上下文信息, 进一步增加了产生式的规模与数量, 也使产生式的抽象程度有所下降.

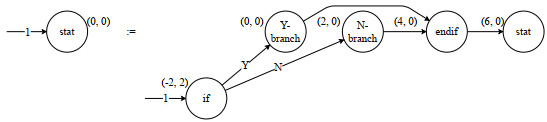
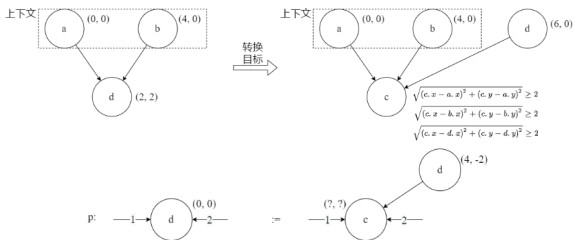
SG、SGG与CGG配置产生式与上下文之间空间语义关系的另一种方法是: 根据图柄结点在主图中与余图的坐标关系, 间接地设计嵌入图结点的坐标信息.图 15是根据这种间接配置方法设计的CGG产生式, 其设计过程为: 首先计算出产生式左图结点“stat”的图柄与主图中上下文的坐标差, 再根据产生式右图结点“if”与左图结点之间的坐标关系分配满足布局要求的“if”结点坐标.然而, 由于缺少产生式与上下文的空间关系的显式描述, 这种间接配置方法的直观性有所不足, 增加了设计人员绘制产生式的难度, 尤其在那些坐标计算较为复杂的应用场景下.例如, 部分图模型布局算法要求相邻结点之间需保持一个合适的距离, 例如力引导布局算法^[22]、Fruchterman-Reingold算法^[23]以及Kamada-Kawai算法^[24].图 16描述了一个要求相邻结点距离不小于2的布局需求, 其中, 图转换后与上下文结点“a”, “b”相邻的结点由结点“d”转变为新增结点“c”.

以CGG为例, 由于产生式中缺少显式的上下文结点“a”和“b”, 导致在产生式设计阶段结点“c”坐标的计算复杂化且易出错, 也在一定程度上增加了产生式设计人员学习曲线的陡峭程度, 不利于布局方法的推广应用.

4 结论与展望

针对空间图文法形式框架存在的问题, 本文对前期工作中构建的坐标图文法CGG进行改进, 通过引入虚结点描述产生式与主图之间的语法结构与空间语义关系, 并构建了一个新的空间图文法形式框架vCGG与几种典型空间图文法形式框架进行对比分析, vCGG具有以下几个优点.

(1) 在产生式中引入虚结点作为上下文结点, 上下文信息得到了显式的描述, 文法具有更好的直观性;

(2) 采用粘合的方式进行图转换操作, 有效防止了转换过程中出现悬边, 操作的规范性得以保证;

(3) 通过虚结点描述上下文与产生式之间的空间语义关系, 在保留上下文抽象性的同时, 使文法具有更全面的空间语义配置性能;

(4) 使用虚结点代替悬边描述上下文, 在增强了文法表达能力的同时, 避免了CGG中的悬边映射问题;

(5) 在归约的过程中, 能够通过较少的产生式更早地发现语法与语义错误并及时停机, 减少了无效归约的数量.

在今后的研究中, 在图文法理论研究方面, 我们将进一步改善空间图文法形式框架, 尝试利用图形元素之间的空间拓扑关系进一步缩小图柄搜索空间, 减小分析算法的时间开销, 使文法的实用性更强.在图文法应用方面, 我们考虑将图形元素的空间特征作为关联属性, 为产生式关联语义动作或条件谓词作为属性文法, 在图转换过程中加入语法制导翻译, 尝试将图文法应用在建筑外观建模、工业设计与验证等领域中, 并开发一个空间图文法系统平台, 为文法操作以及相关应用的落地提供支撑.