2. 高可信软件技术教育部重点实验室, 北京 100871;
3. 北京大学 (天津滨海)新一代信息技术研究院, 天津 300450;
4. 北京大学 软件工程国家工程研究中心, 北京 100871
2. Key Laboratory of High Confidence Software Technologies of Ministry of Education(Peking University), Beijing 100871, China;
3. Peking University Information Technology Institute(Tianjin Binhai), Tianjin 300450, China;
4. National Engineering Research Center of Software Engineering, Peking University, Beijing 100871, China
行走是日常生活中最常见的行为之一, 其中, 行走的速度、方向、步数和步长是感知室内人体状态的重要信息.例如: 根据行走的方向和速度, 我们可以获得人在室内的移动轨迹, 为室内定位和追踪提供帮助; 通过记录一天中人行走的时间和步数, 可以统计人的日常运动量信息; 而行走的速度和步长特征也反映了人的步态特征, 可以用于判断人的身份和健康状态等高级语义.因此在近几年中, 对行走行为的识别和重要参数的感知, 受到研究人员的广泛关注.
为了识别行走, 估计人的行走参数, 研究人员提出了多种感知技术.例如, 基于可穿戴设备的方法、基于环境传感器的方法、基于计算机视觉的方法等.基于可穿戴设备的方法[1, 2]是最早被用来识别行走行为并获得相关参数的方法, 然而这种方法要求用户时时刻刻穿戴感知设备, 同时还需要不定时地更换电池或为设备蓄电, 给人们的生活带来不便.尤其是对于家里的老年人和小孩子, 随时携带设备的要求很难被满足.基于周围环境设备的方法[3, 4]尝试通过在环境中部署雷达、声音感知和地板震动感知等特殊设备, 非侵入地实现行走行为的识别和行走参数估计, 但是由于需要在居住环境中部署这些专用的感知设备, 所以成本较高.基于计算机视觉的方法[5, 6]通过摄像头获取室内图像或视频信息进行行走识别, 并计算行走的相关参数, 但是存在隐私担忧和视线要求等问题.到目前为止, 可被用于日常家庭中的低成本、非接触式的行走识别和行走参数估计技术依然缺失.
近年来, 随着Wi-Fi技术的迅速发展, 利用家庭中普遍存在的Wi-Fi设备进行行走识别和行走参数估计受到了研究人员的关注.一方面, 复用环境中已有的Wi-Fi设备进行感知不仅不需要增加任何感知成本, 同时也保护了用户的隐私; 另一方面, 由于Wi-Fi信号具有穿墙能力, 所以相比于声音、光信号等, 感知范围较大.由于这些优势, 越来越多的基于Wi-Fi的感知技术涌现出来, 其中, 对于行走行为的感知也做了大量的工作.E-eyes[7]、CARM[8]通过观察Wi-Fi信号信道状态信息(channel state information, 简称CSI)的振幅变化, 提取了振幅直方分布、振幅变化频率等特征对包括行走在内的几种日常行为进行了识别, 但需要事先离线采集大量数据, 进行分类模型或判定阈值的学习.除此之外, Wi-Fi信号也被尝试用来识别人的步态信息.WifiU[9]、WiWho[10]发现: 不同人在行走时由于步频、步幅的不同, 对Wi-Fi信号的影响也不相同.他们通过人在行走过程中造成的时域和频域的信号波动, 识别出人行走的每一步, 并提取相应的特征, 实现了对人的步态识别, 但都要求人必须沿一个方向且预定义好的固定路线行走.WiDir[11]基于多载波菲涅尔区模型来实现人行走方向的识别.不同子载波由于波长不同, 其构成的菲涅尔区大小也不相同.人在行走过程中依次穿越各个子载波的菲涅尔区, 造成延时.延时同时又与行走的方向有关, 不同的行走方向会产生不同的延时效果.WiDir通过捕捉这种延时, 进而实现了人行走方向的判别, 但是由于需要积累足够长时间的信号以计算子载波间的延时, 所以WiDir要求人走动一段时间后才能得知人行走的方向.WiStep[12]利用CSI信号的时域相关性, 将走动与原地活动做区分, 需要事先离线采集大量数据以训练机器学习模型.同时, 它提取人行走时波动幅度最大的子载波对应的短时能量变化和频率变化来统计人行走的步数, 但却需要采用定向天线, 因而影响了Wi-Fi的正常数据通信.
然而, 上述这些方法在识别行走行为时, 均假设人在行走前后会保持静止, 利用信号从稳定到剧烈波动这一变化过程实现行走的识别.因此, 为了能够获得可以区分行走和静止状态时信号差异的阈值, 这些方法都需要耗费大量的人力进行离线的训练和学习.此外, 在日常生活中, 这一假设本身也往往很难满足.在自然生活状态下, 人们通常在走路前后并不一定处于静止状态, 往往伴随着其他的原地活动.像一个人起床后, 他会首先在床边叠被子, 然后紧接着行走到卫生间洗漱.这种常见的原地活动与行走连在一起的系列活动, 会使这些基于信号波动性来识别行走行为的系统产生大量的误报.另一方面, 为了实现行走参数的估计, 目前的工作或是对人的行走方式进行严格的要求, 或是对现有的Wi-Fi设备做出硬件上的修改, 当人的行走路线、速度、所处环境发生变化或者采用商用Wi-Fi设备时, 行走参数估计的性能将大为下降.
到目前为止, 现有方法为了从Wi-Fi信号中提取出反映人行走信息的信号特征, 主要依赖于大量的经验观察, 所提取的信号波动性、时域相关性等特征与行为间的映射关系较为间接; 且由于缺乏理论指导, 所提取的特征中往往会包含与环境和感知目标相关的多余信息, 造成系统学习成本高、鲁棒性较差.不同于以往工作, 本文通过分析人在行走过程中产生的多普勒效应和Wi-Fi信道状态信息之间的关系, 建立了多普勒速度运动模型, 揭示了行走行为和信道状态信息变化之间的理论关联, 从而在不需要任何学习的情况下, 实现了行走识别和行走速度、方向、步数和步长等参数的估计.具体地, 为了将走路与其他原地活动区分开, 一个基本观察是: 人在进行原地活动时, 他的位置是在一个很小的范围内无规律的变化, 而人在走动时, 其位置会在特定方向上连续变化, 位置的变化范围较大.基于该观察, 我们通过从Wi-Fi信号中提取出由于人活动引起的多普勒频移, 并将其转化为多普勒速度.由于多普勒速度和人的活动具有直接的映射关系, 所以利用多普勒速度, 我们可以进一步获得一段时间内人的位置变化范围, 从而将行走与其他原地活动区分开, 实现了对行走行为的识别.此外, 为了估计行走的参数, 本文分析了多普勒速度和人的行走速度之间的关系, 然后通过结合两个Wi-Fi设备上获得的多普勒速度, 实现了人行走速度和行走方向的估计.最后, 由于人在行走时, 其身体在每一步表现为一个先加速后减速的过程, 所以行走速度将会先增大然后再减小.基于这种速度变化的规律, 我们实现了精准的步数和步长估计.
本文第1节回顾相关工作.第2节分析人的活动引起的多普勒速度和信号信道状态信息之间的关系.第3节具体介绍如何根据多普勒速度实现行走的识别和估计行走参数.第4节从行走的识别和行走参数的估计两个角度用实验充分评估系统性能.最后, 第5节总结全文内容.
1 相关工作近几年, 研究人员提出了各种各样的用于室内人体感知的技术, 例如现在流行的基于计算机视觉的感知技术、基于周围环境设备的感知技术、基于红外线的感知技术和基于穿戴传感器的感知技术等.然而, 基于计算机视觉的感知技术[5, 6]一般是通过一组高分辨率的摄像头记录人活动时的录像, 并通过图像分析和处理技术实现对人的行为感知, 需要较好的光照条件; 并且因为家具、物品的遮挡, 存在视觉的死角.另外, 在家庭等室内环境安装摄像头会带来比较严重的隐私问题; 基于周围环境设备的感知技术试图分析环境中声音、振动传感器或雷达设备的信号变化来感知人的行为[3], 这种方法虽然解决了隐私、光线、遮挡等方面存在的问题, 但需要将特定的设备植入到环境中, 一方面成本非常高, 另一方面会受到环境中其他传感压力源或周围一些物体噪声的影响; 基于穿戴传感器的感知技术利用加速传感器去感知速度和加速度[2], 但需要感知目标时刻携带手机、穿戴传感器等特定的设备, 并且需要定时地为设备进行充电.因为现有技术的不足, 研究人员开始尝试寻求新的、低成本的、非接触的技术来实现行走的识别和行走参数的估计.
相比于其他技术, 逐渐兴起的Wi-Fi感知技术因其感知范围广、非侵扰、保护隐私等优势, 吸引了大量科研工作者开始研究无线信号变化和人行为活动之间的关系.特别是从商业Wi-Fi设备上获取的信道状态信息(channel state information, 简称CSI)在正交频分复用(orthogonal frequency division multiplexing, 简称OFDM)子载波的层次上揭示了比传统MAC层接收到的信号强度RSS(received signal strength, 简称RSS)更加细粒度的多路径传播特性, 使得利用无线信号刻画行为活动的信息更加丰富.利用CSI的振幅和相位信息以及在MIMO (multiple input and multiple output)系统中多天线上CSI的差异性, 基于Wi-Fi CSI的人体行为感知工作可以分为三大类: 第1类是对目标存在性的感知, 像最开始出现的一系列通过从CSI振幅、相位信号中提取特征(如信号的时域相关性、滑动方差、直方图分布等)来探测感知目标是否存在于感知环境中的工作[13-17]; 第2类是对人位置信息的感知, 像室内定位[18, 19]、室内追踪[21, 22]; 最后一类是对人体行为状态的感知工作[7-12, 23-36], 由于与行走行为较相关, 所以我们将对这一类展开介绍.大量的对人体行为状态的感知工作根据感知行为的粒度, 进一步又可以分为两个子类.
● 第1类是对小尺度行为活动的感知: 像Wikey[23]利用敲击键盘时引起的不同子载波上CSI振幅变化的相关性, 实现了对人的不同击键行为的识别; WiFinger[24]利用不同的手指运动对CSI振幅的影响不同, 通过提取CSI的振幅随时间变化的特征, 结合机器学习算法实现了不同的手指手势识别; WiHear[25]则是利用人在说话时嘴唇和舌头运动方式的不同, 会造成CSI振幅产生不同频率的波动, 以此来识别人发出的具体音节; 除此之外, Wi-Fi信号也被用来感知人的心跳和呼吸等生理特征[26, 27, 30], 其主要原理是: 人在呼吸时, 胸部的起伏会导致CSI振幅产生规律性的波动, 通过对振幅信号进行频率分析就可以获得呼吸的频率.类似地, 人的心脏跳动也会引起对应心跳频率的信号变化;
● 第2类是对大尺度行为活动的感知: 像WiFall[31]和RTFall[32]分别利用了振幅和相位差作为基本信号, 实现了跌倒行为的识别; WiFit[33]利用不同的健身行为在信号上产生的不同的多普勒频移特征, 实现了对3种健身运动的识别.除了这些工作, Wi-Fi信号也被尝试用来感知人的行走.E-eyes[7]系统首先利用信道状态信息(CSI)的方差来识别行走的开始和结束, 并且利用CSI振幅的变化特征来实现行走轨迹的识别.然而, 该系统需要首先进行离线采集大量数据进行学习, 才能实现行走的识别与轨迹判断. CARM[8]系统则搭建了一个行为识别系统来区分行走、跑、坐下、摔倒等日常行为, 然而该系统假设不同行为之间存在一段静止状态从而实现行为的切分, 且需要通过学习建立分类模型后才能进行行走行为的识别.WifiU[9]系统同样利用CSI信号波动的方差来识别行走, 并从CSI振幅的时频特征中识别步态.WiWho[10]系统则利用Wi-Fi信号在频域的能量差异来区分行走和其他行为, 然后根据CSI振幅的变化来识别不同人的步态, 实现不同人的身份识别.然而, WifiU和WiWho都要求人沿固定的一条路线行走, 当人沿其他路线行走时, 其识别性能将大为下降.WiDir[11]系统利用人在沿不同方向穿越菲涅尔区时, 不同子载波信号变化延时的不同, 实现了对人行走方向的识别, 但需要人在走动一定时间之后才能判别出人的行走方向, 且无法获得细粒度的行走步数、速度等信息.WiStep[12]系统通过提取Wi-Fi CSI信号的时域和频域特征, 然后结合机器学习算法实现了行走的识别和步数的统计, 需要定向天线将信号能量集中在人的行走区域内.
一方面, 为了实现行走行为的识别, 以上这些工作利用CSI振幅或相位信号的波动性或时域相关性, 所以需要人在行走前后保持静止状态来维持信号的稳定, 最后通过与事先离线学习获得的阈值进行比较来实现对行走的识别; 另一方面, 为了实现行走参数的估计, 大量工作依据经验观察提取了行走状态相关的信号特征, 但是由于所提取的特征与人的行走行为的映射关系模糊, 所以需要对人的行走方式、感知环境或感知设备进行限制, 以尽量保证映射的稳定性.与上述工作相比, 本文期望通过分析人在行走过程中产生的多普勒效应和Wi-Fi信道状态信息之间的关系, 从模型的角度揭示行走行为和CSI变化之间的理论关联, 从而在不需要任何学习的情况下, 实现行走识别和行走速度、方向、步数等参数的估计.
2 多普勒效应与信道状态信息为了利用Wi-Fi信号来识别行走和估计行走参数, 首先需要回答两个基本问题: (1) 人的活动是如何影响Wi-Fi信号的?(2) 如何从Wi-Fi接收信号中提取出可以反映人运动状态的信息?在本节中, 为了回答上述两个问题, 这里将首先介绍基于Wi-Fi信道状态信息(CSI)的多普勒速度模型, 建立起人运动过程中引起的多普勒速度和Wi-Fi CSI之间的关系, 然后将具体介绍如何从CSI信息中获取多普勒速度来描述人的活动.
2.1 基于CSI的多普勒速度模型如图 1所示, 给定一对Wi-Fi收发设备, 信号可以从发射端(TX)沿直接通路传播到接收端(RX), 也可以经过墙壁、人体等其他物体的反射到达接收端, 最终导致接收端接收到的是沿多条路径传播叠加后的信号, 这种信号沿多条路径传播的现象也称为多径效应.
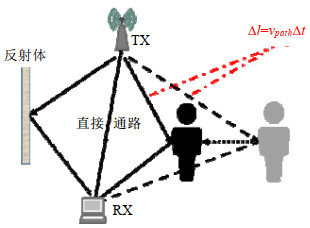
|
Fig. 1 As signal propagates from transimitter to receiver by multi-path, human movement will change the reflection path length which would introduce a Doppler frequency shift 图 1 信号会沿多条路径传播到达接收端, 而人的移动会造成其反射路径长度发射变化, 相应地会在接收信号上产生多普勒频移 |
当人在环境中活动时, 也会作为一个信号反射体, 发射信号会经过人的反射到达接收端, 而人的运动相应地会造成这条反射信号的传播路径长度发生变化.由于接收端接收到的是所有多径叠加的信号, 包含经过人反射到达接收端的信号, 所以, 由于人的活动引起的反射信号的传播路径长度变化也会体现在接收端接收到的叠加信号中, 具体表现为接收端接收到信号上会产生由于人运动造成的多普勒频移, 数学表达如下:
| ${f_{Doppler}} = f\frac{{{v_{path}}}}{c}$ | (1) |
其中, f为信号传播的载波频率, vpath为人运动造成的反射路径的路径长度变化速度, c为光速.由于多普勒频移直接由人的活动引起, 所以如果可以从信号中估计出该多普勒频移, 就可以通过它来描述人的活动.而为了估计出多普勒频移, 就不得不介绍一个重要的概念——信道状态信息(CSI).通信中, 一个典型的无线通信系统可以在频域建模为
| $y=Hx+n $ | (2) |
其中, x为发送端发送信号的数学表示, y为接收端接收信号的数学表示, n代表信道噪声.那么, H就是我们所说的信道状态信息(CSI), 它描述了信号沿不同路径传播过程中造成的信号振幅衰减和信号相位偏移.在最简单的只有一条传播路径的情况下, CSI的数学表达如公式(3)所示:
| $H(t)=A{{\text{e}}^{-j2\text{ }\!\!\pi\!\!\text{ }f\tau }} $ | (3) |
其中, A代表振幅的衰减; τ代表信号沿该路径从发射端传播到接收端所用的时间, 也称为传输时延; f为信号传输的载波频率; e-j2πfτ代表由于传输时延造成的相位偏移.
假设t0时刻, CSI的表达为H(t0)=Ae-j2πfτ, 人的活动会造成由人引起的反射信号的传播路径长度发生变化.如果这个变化速度为v, 那么在一个很短的时间Δt之后, 由于人运动产生的多普勒频移将会反映在CSI上, 忽略振幅衰减A的变化, t0+Δt时刻的CSI将有如下表达:
| $H({t_0} + {\rm{\Delta }}t) = H({t_0}){{\text{e}}^{ - j2\pi {f_{Doppler}}{\rm{\Delta }}t}} = H({t_0}){{\text{e}}^{ - j2\pi fv{\rm{\Delta }}t/c}} = A{{\text{e}}^{ - j2\pi f(\tau + v{\rm{\Delta }}t/c)}}$ | (4) |
在只有一条传播路径的情况下, 多普勒频移的产生使得t0+Δt时刻的CSI相对于t0时刻的CSI发生了相位变化.而在充满了墙壁、桌椅等反射体的室内环境中, 发射和接收端之间存在着丰富的反射路径, 信号将会从发射端发出, 同时沿这些反射路径进行传播到达接收端.那么考虑这种多条传播路径的场景, 相应地, CSI可以表达为多条路径的叠加:
| $H({t_0} + {\rm{\Delta }}t) = \sum\limits_{l = 1}^L {{A_l}{{\rm{e}}^{ - j2\pi f({\tau _l} + {v_l}{\rm{\Delta }}t/c)}}} $ | (5) |
其中, L为多径环境中发射端和接收端之间传播路径的个数, Al代表t0时刻第l条传播路径对应的振幅衰减, τl代表t0时刻信号从发射端沿第l条路径传播到接收端所需时间, vl代表第l条路径的传播路径长度变化速度.那么根据vl是否为0, 我们可以把环境中的传播路径分为两类: 一类是直接通路以及由墙壁、天花板等静态物体反射引起的反射路径, 它们的路径长度并不随时间发生变化, 所以vl=0, 我们把这些静态传播路径叠加而形成的CSI记为常数HS; 除了这部分静态路径以外, 另一类就是由于人活动产生的动态传播路径, 其路径长度随着人的运动会发生变化, 所以vl≠0, 我们把这部分动态路径叠加形成的CSI记为HD(t0+Δt), 进一步地, 公式(5)可以表示为
| $ H({t_0} + {\rm{\Delta }}t) = {H_S} + {H_D}({t_0} + {\rm{\Delta }}t) = {H_S} + \sum\limits_{l = 1}^L {{A_l}{{\rm{e}}^{ - j2\pi f({\tau _l} + {v_l}{\rm{\Delta }}t/c)}}} $ | (6) |
由公式(6)可知, CSI的相位与传播路径长度的变化速度vl紧密相关.具体地, 相位变化的频率就对应传播路径长度的变化速度vl.而vl是由于人运动造成的, 所以如果可以获得CSI相位的变化, 就可以获得路径长度的变化速度vl, 从而推演出人的活动状态.接下来, 我们将具体介绍如何从CSI中获取传播路径长度的变化速度vl——多普勒速度.
2.2 基于MUSIC的多普勒速度估计实际中, 从商业Wi-Fi设备的CSI中提取多普勒速度仍然面临着一个挑战, 它的相位变化并不能直接反映出多普勒速度.这是因为, 在发射设备和接收设备分离的通信系统中, 发射和接收设备的时钟并不能完美地同步, 使得它们在通信时生成的载波频率会有所偏差[20], 接收端相对于发射端的这个载波频率偏差Δf会给测量的CSI带来一个随着时间变化的相位误差ejΔft, 导致t0+Δt时刻实际测得的CSI表达如下:
| $H({{t}_{0}}+\Delta t)={{\text{e}}^{j\Delta ft}}{{H}_{ideal}}({{t}_{0}}+\Delta t) $ | (7) |
这个时变的相位误差和多普勒速度造成的相位变化混合在一起, 会导致无法准确地从CSI中估计出多普勒速度.为了消除这个相位误差, 我们利用的一点观察是: 目前常见Wi-Fi网卡均支持至少3根天线, 而同一个网卡两根接收天线由于共用同一个时钟振荡器, 所以CSI的相位误差是相同的.因此, 可以通过将两根天线的CSI做共轭乘法来消除相位误差φ(t), 具体数学表达如下:
| ${H_{new}} = {H_1}({t_0} + {\rm{\Delta }}t) \cdot H_2^*({t_0} + {\rm{\Delta }}t) = {{\mathbf{e}}^{\boldsymbol{j}{\rm{\Delta }}ft}}{H_1}({t_0} + {\rm{\Delta }}t) \cdot {{\mathbf{e}}^{ - \boldsymbol{j}{\rm{\Delta }}ft}}H_2^*({t_0} + {\rm{\Delta }}t) = {H_1}({t_0} + {\rm{\Delta }}t) \cdot H_2^*({t_0} + {\rm{\Delta }}t)$ | (8) |
其中, H1(t0+t)表示天线1
| $ \begin{array}{l}{H}_{new}=[{H}_{1S}+{H}_{1D}({t}_{0}+\rm{Δ}t)]\cdot {[}^{{H}_{2S}}\\ \;\;\;\;={H}_{1S}\cdot {H}_{2S}^{*} + {H}_{2S}^{*}\cdot {H}_{1D}({t}_{0}+t) + {H}_{1S}\cdot {H}_{2D}^{*}({t}_{0}+t) + {H}_{1D}({t}_{0}+{\rm{\Delta }}t)\cdot {H}_{2D}^{*}({t}_{0}+t)\end{array}$ | (9) |
H1S、H2S分别表示天线1和天线2中静态路径部分对应的CSI表达, 所以可以看成是一个新的常数项; 而H1D(t0+Δt)和H2D(t0+Δt)分别表示天线1和天线2中动态路径部分对应的CSI表达, 它随时间的变化反映着多普勒速度, 所以公式(9)中包含这两部分的第2项与第3项是我们关注的部分.另外, 由于静态路径中包含直接通路, 所以动态路径与静态路径相比能量较小, 那么,
| ${H'_{new}} = {H_{1S}} \cdot H_{2S}^* + H_{2S}^*{H_{1D}}({t_0} + t) = {H'_s} + \sum\limits_{l = 1}^L {{{A'}_l}{{\rm{e}}^{ - j2\pi f({\tau _l} + {v_l}t/c)}}} $ | (10) |
由公式(10)可知, 新的CSI的相位变化再一次对应于人运动引起的多普勒速度.由于静态路径不随时间变化, 所以其造成的多普勒速度永远为0, 为了只关注由于人引起的非零的多普勒速度, 我们通过减复数均值的方式将
| ${H_{final}} = \sum\limits_{l = 1}^L {{{A'}_l}{{\rm{e}}^{ - j2\pi f({\tau _l} + {v_l}t/c)}}} $ | (11) |
Hfinal为多条动态路径叠加而成的信号, 从一个叠加信号中分离各个目标信号, 是通信领域中的重要问题.其中一个比较经典的方法就是多重信号分类算法(mutiple signal classification algorithm, 简称MUSIC), 该方法的基本思想是: 通过将叠加的信号进行特征值分解而构造出信号空间和噪声空间, 然后利用信号空间和噪声空间的正交性对目标信号进行估计.具体地, 假设环境中只有一条传播路径, 一段时间窗口内Hfinal的采样个数有M个(采样时间均匀), 那么由于多普勒速度的存在, Hfinal的相位会随着时间发生规律性的变化.在M个采样之间产生相位差, 以第1个采样的相位为基准, 则之后的采样相对于第1个采样的相位差可以表示为
| $\vec a(v) = [1, {{\rm{e}}^{ - j2\pi fv{\rm{\Delta }}t}}, {{\rm{e}}^{ - j4\pi fv{\rm{\Delta }}t}}, ..., {{\rm{e}}^{ - j2(M - 1)\pi fv{\rm{\Delta }}t}}]$ | (12) |
| $\begin{array} {l} {H_{matrix}} = [H_{final}^{{t_0}}, H_{final}^{{t_0} + {\rm{\Delta }}t}, ..., H_{final}^{{t_0} + (M - 1){\rm{\Delta }}t}] = \sum\limits_{l = 1}^L {\vec a({v_l}){H_l}({t_0}) + N} \\ \;\;\;\;\;\;\;\;\;\;\;\;= [\vec a({v_1}), \vec a({v_2}), ..., \vec a({v_L})][{H_1}({t_0}), {H_2}({t_0}), ..., {H_L}({t_0})] + N \\ \;\;\;\;\;\;\;\;\;\;\;\; = AH + N \end{array} $ | (13) |
基于MUSIC算法的基本思想对Hmatrix进行特征值分解, 得到相关矩阵Hcorr:
| ${{H}_{corr}}=E=AE[H\cdot H{}^\circ ]A{}^\circ +E[N\cdot N{}^\circ ] $ | (14) |
相关矩阵Hcorr存在M个特征值, 其中, M-L个小特征值对应的特征向量构成了噪声空间EN, L个大特征值对应的特征向量构成了信号空间.而根据信号空间和噪声空间的正交性, 利用信号向量
| $P(v)=\frac{1}{{{{\vec{a}}}^{{}^\circ }}(v){{E}_{N}}E_{N}^{{}^\circ }\vec{a}(v)}$ | (15) |
如图 2(a)所示为真实实验估计获得的多普勒速度谱, 图中最高峰的位置对应的就是一条动态路径对应的多普勒速度.而积累一段时间的多普勒速度谱之后, 就可以获得多普勒速度随时间的变化, 我们称其为时间-多普勒速度谱, 如图 2(b)所示.该图展示了一个人胸前手持铁板首先靠近收发设备, 然后倒退远离收发设备这一过程中对应的多普勒速度变化.从图中可以看出: 时间-多普勒速度谱不仅可以体现多普勒速度大小的变化, 也包含着速度的方向信息.当人在9s~17s靠近铁板时, 由于人与收发设备的距离逐渐变小, 所以反射信号传播路径的长度逐渐变小, 多普勒速度为负值.并且, 由于人是从静止启动, 加速到速度最大, 最后停止.相应地, 其多普勒速度的绝对值从0逐渐增大最后减为0;而当人在17s~24s远离收发设备时, 反射信号传播路径的长度则逐渐增加, 多普勒速度为正值.由于人是从开始启动倒退远离收发设备, 逐渐加速, 到最后停下静止的运动过程, 所以多普勒速度的绝对值也是从0逐渐增大最后减为0.由此我们可以知道: 多普勒速度随着时间的变化可以反映人的运动方向、加速、减速、静止等信息.进一步我们将具体介绍如何利用多普勒速度来进行行走识别和行走参数估计.
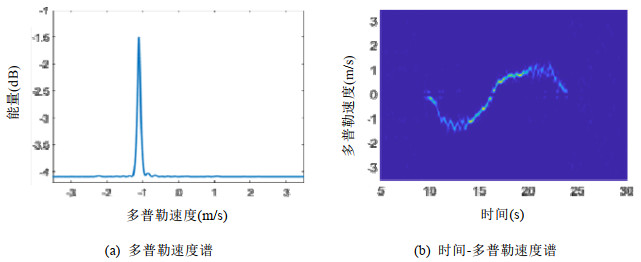
|
Fig. 2 图 2 |
3 基于多普勒速度的行走识别和行走参数估计
多普勒速度反映着丰富的人的运动信息, 但它是反射路径长度的变化速度, 与人的真实运动速度相关, 又不完全等价于人的真实运动速度.所以在这一节中, 首先具体分析人的真实运动速度与多普勒速度之间的关系, 然后介绍行走的识别以及行走的速度、方向、步数和步长等参数的估计方法.
3.1 人的真实速度与多普勒速度如图 3(a)所示, 给定一对Wi-Fi收发设备, 存在一个以收发设备为焦点、经过人的椭圆.当人在运动时, 人真实的运动速度可以分解为沿椭圆切向方向的切向速度分量和沿椭圆法向方向的法向速度分量.由于多普勒速度为反射路径长度的变化速度, 而根据椭圆的性质又可知, 切向速度分量并不会改变反射路径的长度, 所以多普勒速度的产生只与法向速度分量有关.也就是说, 多普勒速度可以反映人的真实运动速度的部分信息.为了描述完整的人的真实的运动速度, 这里我们引入二维多普勒速度模型.
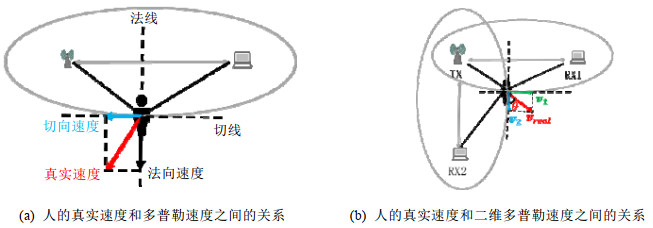
|
Fig. 3 图 3 |
如图 3(b)所示, 给定一个发射设备、两个垂直摆放的接收设备, 当人处于两对收发设备构成的感知区域内时, 分别存在两个以收发设备为焦点、经过人的椭圆.图中vreal为人的真实运动速度, v1为vreal在椭圆TX-RX1上的法向速度分量, v2为vreal在椭圆TX-RX2上的法向速度分量.
如图 3(a)所示: 因为反射信号从人体经过一个往返的路程到达接收端, 所以路径长度的改变量可以近似为人在法向方向移动的距离的2倍[8].也就是说, 多普勒速度可以近似为法向速度的2倍.在图 3(b)中, 假设RX1感知到的多普速度为vdoppler1, 可以近似认为人在该椭圆的法向向上的运动速度分量v1≈vdoppler1/2.同理可获得v2.根据v1和v2, 就可以求得人的真实速度vreal, vreal的大小和方向, 可以表达如下:
| $\left\{ {\begin{array}{*{20}{l}} {{v_{real}} \approx \sqrt {v_{dopple1}^2/4 + v_{doppler2}^2/4} } \\ {\theta \approx \arctan \frac{{{v_1}}}{{{v_2}}}} \end{array}} \right.$ | (16) |
建立起人真实的运动速度和多普勒速度之间的关系之后, 本节将具体介绍如何利用多普勒速度从日常行为中切割出行走以及估计出行走相应的参数.考虑到人在生活中的日常行为, 可以将常见的日常行为分为3类:
(1) 静止行为, 像睡觉、看电视等;
(2) 原地行为, 像做饭、刷牙、洗澡等;
(3) 行走行为, 像从灶台走到餐桌或从一个卧室移动到另一个卧室.
在日常生活中, 人在行走前后可能是静止不动的, 也可能伴随着一些原地行为.例如, 一个老人在做饭后(原地行为)行走到餐桌旁坐下吃饭(原地行为), 那么如何将行走与这些原地行为区分开便很关键.为了区分行走行为和原地行为, 利用的一个关键观察是: 原地行为往往发生在特定的位置, 像在灶台旁做饭, 洗手池旁洗漱, 这时人的位置是在一个很小的范围内且无规律的变化; 而人在行走时则不同, 他会在某个方向上发生一定的位移, 位置的变化范围较大且有规律.基于此观察, 在一段时间窗口, 根据估计出的人的速度就可以获得人的多个近似位置, 那么必然存在一个直径最小的圆将这些位置完全覆盖住, 我们定义这个圆为覆盖圆.
如图 4所示, 我们通过摄像头记录了一个实验者在智能家庭中进行不同的日常活动时, 他的真实的位置变化情况.图 4(a)为一个实验者坐卧在沙发上看电视时对应的位置变化情况(蓝色的圆点); 图 4(b)是他在灶台旁做饭时对应的位置变化情况; 图 4(c)是他起床后在床边穿衣服, 然后从主卧行走到卫生间, 在洗手池旁洗漱的整个过程中, 他的位置变化情况.图中覆盖蓝色点的大圆就是不同行为对应的覆盖圆, 其覆盖圆的直径就表示了在这段时间内人位置的变化范围.从图中可以看出: 静止行为对应的覆盖圆直径为0, 而行走行为对应的覆盖圆直径明显大于原地行为.所以可以依据覆盖圆直径的大小来判断走动的发生: 如果直径大于一定范围, 则表示走动发生; 否则, 则是静止或原地活动.

|
Fig. 4 Real location variation and covering-circle for different activities 图 4 不同行为在一段时间真实的位置变化和覆盖圆直径 |
如图 5所示, 为了进一步证明利用多普勒速度推导出的位置变化也具有该性质, 我们又让实验者在Wi-Fi设备的感知区域中真实地进行了一系列短时间的日常活动, 利用多普勒速度和真实速度之间的关系, 我们可以获得这一系列日常活动相应覆盖圆直径的变化情况.整个过程中, 他开始先在灶台旁做饭, 然后行走到餐桌旁坐下来吃饭, 吃完饭后接着走到洗碗池旁刷碗, 最后又回到餐桌旁收拾桌子并结束整段活动.从图 5中覆盖圆的直径变化可以看出: 不同种类的日常活动对应的覆盖圆的直径大小不同; 特别地, 走路对应的覆盖圆直径明显大于其他的原地活动.所以, 依据多普勒速度可以获得不同行为对应的覆盖圆直径的大小, 从而将行走从连续的日常活动中识别出来.具体地, 在实际系统中采用了2s的时间窗口, 判断走动发生的覆盖圆直径取值为0.8m.
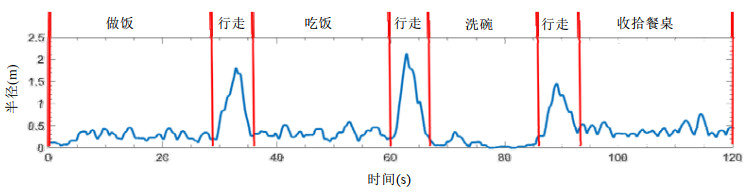
|
Fig. 5 Diameter variation of covering-circle for a series of daily activities 图 5 一系列日常活动对应的覆盖圆的直径变化 |
3.3 行走参数估计
识别出行走行为之后, 为了更加细粒度地描述该段行走, 往往需要知道行走的速度、方向、步数和步长等参数.对于行走的速度大小和方向, 由第3.1节我们知道, 可以利用公式(8)多普勒速度与人的真实速度之间的数学关系推导求出人的行走速度vreal和行走方向θ.
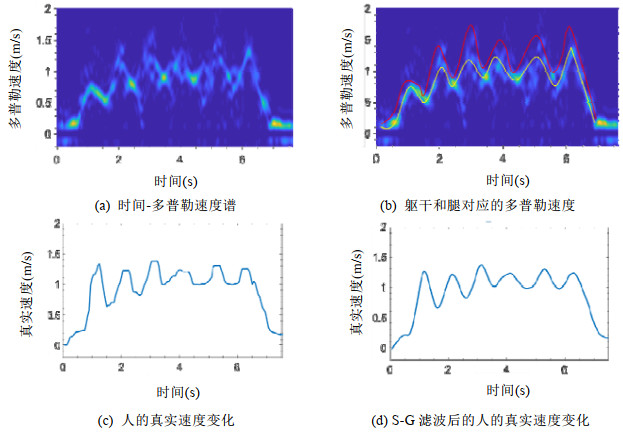
除了行走方向和速度, 行走的步数和步长也是描述走路的重要参数.为了统计行走的步数和估计出行走的步长, 就需要理解人在每一步行走过程中对信号的影响, 识别出每一步行走.人在行走中的一步是一只脚离开地面到该只脚落地, 而另一只脚准备离开地面的过程.在这个过程中, 连接主动脚的腿呈现出一个先加速后减速的过程, 相应地, 身体躯干也会连动着呈现出一个先加速后减速的过程.如图 6(a)展示了人在自由行走6步时一台接收设备所获得的时间-多普勒速度谱.相比于图 2(b)中人手持铁板产生的时间-多普勒速度谱, 图 6(a)的速度谱中速度成分更加复杂一些, 这是因为, 铁板相比于人体的反射能力要强很多, 所以在人手持铁板运动的过程中, 人体其他部位产生的反射路径可以完全被忽略掉, 可以近似看成由铁板产生了一条动态反射路径; 而当去掉铁板, 人在自由行走时, 无论是躯干还是腿部、头部反射能力是相同的, 只是在反射面积上存在差异, 所以这时身体各个部位运动产生的多普勒速度都会体现在时间-多普勒速度谱上.如图 6(b)所示, 谱中能量最亮的带对应的是躯干引起的多普勒速度(白色轮廓线), 这是因为躯干的面积最大, 所以产生的多普勒速度能量最强.但仔细观察, 我们还会发现谱中存在一条能量较弱但是速度较大的带(红色轮廓线), 这是人在行走时腿部产生的多普勒速度, 因为腿部是行走时的动力来源, 所以要比躯干的速度大一些, 但同时, 由于腿部的反射面积较小, 所以产生的多普勒速度能量较弱.因为躯干产生的多普勒速度较明显, 更有利于提取, 所以我们主要关注行走中躯干产生的多普勒速度.进一步观察身体躯干的多普勒速度变化, 我们可以发现, 每一步行走对应的身体躯干的多普勒速度呈现出一个先加速后减速的过程, 这与人行走时身体躯干速度先加速后减速的过程相对应.最后, 通过结合两台设备的多普勒速度, 依据第3.1节中公式(8)就可以获得人在行走过程中真实的速度变化情况, 如图 6(c)所示.从图 6(c)中的加速和减速过程可以粗糙地得到行走的步数, 但是, 由于身体在行走过程中的晃动, 得到的速度曲线毛刺较多, 会影响计步的准确性.为了进一步剔除这些身体微小晃动带来的影响, 我们使用了Savitzky-Golay (S-G)滤波对速度进行平滑处理, 它可以在去除无关毛刺的同时保持原来波形的形状和宽度不变, 被经常用于图像的平滑去燥处理中, 图 6(d)所示为S-G平滑之后的速度变化曲线.最后, 通过统计峰值的个数可以识别出每一步行走, 从而实现对行走步数的统计.
|
Fig. 6 图 6 |
当识别出每一步行走之后, 利用速度随时间的变化, 就可以进一步估计行走的步长.具体地, 步长为身体行走一步时移动的距离, 通过对速度在时间上进行积分, 就可以获得每一步的步长.最后对一段行走过程取均值, 就可以估计出人行走时的平均步长.如公式(17)所示:
| $av{{g}_{stride\_Len}}={\sum\limits_{n=2}^{N-1}{\left[ \int\limits_{{{t}_{{{n}_{start}}}}}^{{{t}_{{{n}_{end}}}}}{V(t)} \right]}}/{(N-2)}\;$ | (17) |
为了去掉人在启动和停止时的影响, 计算步长时, 我们去掉了一段走路中的第1步和最后一步, 其中, N代表一段走动中包含的总的步数,
其中, 图 6(a)所示为人行走6步, 一个接收设备上所获得的时间-多普勒速度谱; 图 6(b)所示为躯干和腿对应的多普勒速度变化轮廓; 图 6(c)所示为结合两个接收设备的多普勒速度获得到的人的真实速度; 图 6(d)所示为经过S-G平滑滤波后的人的真实速度
4 实验验证在这一部分, 我们将首先介绍实验设置, 然后分别从行走识别和行走参数估计两方面来评估系统性能.具体地: 对于行走识别, 本文在不同人、不同环境下验证了系统性能; 而对于行走速度、方向、步数和步长等参数估计, 我们验证了不同行走速度、不同行走方向、不同人、不同环境下的影响.
4.1 实验设置实验中, 整个系统包含一个Wi-Fi发射设备和两个Wi-Fi接收设备, 分别利用了技嘉的MiniPC作为发射设备和接收设备.其中, 发射设备需要一根发射天线; 为了消除相位误差, 接收设备需要两根接收天线, 而当前的Wi-Fi设备均支持3根天线, 所以使用其中任意两根天线即可.收发设备均安装了华盛顿大学开放的CSI Tool[37]网卡驱动, 用来从网卡中提取CSI信息.考虑到人行走的速度通常小于3m/s, 为了足以捕获人行走引起的多普勒频移, 在实验中, CSI的采样率设为200Hz.针对每一次多普勒速度谱估计, 采用0.3s的时间窗口内的CSI作为采样用于MUSIC算法.系统可以工作在商用的2.4G或5G频段上, 我们的实验均在5G频段20MHz带宽进行, 且系统对硬件未作任何修改, 对获取CSI的数据包的类型也不作任何要求, 所以在感知数据的采集过程不会影响正常的数据通信.
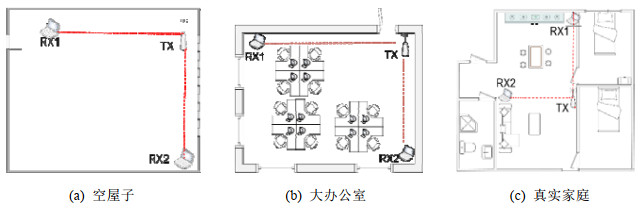
4.2 行走识别的性能为了充分验证行走识别的性能, 如图 7所示, 我们在3个典型的环境中进行了实验: 一个空屋子(如图 7(a)所示)、一个大的办公室(如图 7(b)所示)和一个真实的家庭(如图 7(c)所示).其中, 办公室和家庭厨房中有着大量的家具, 是丰富的多径环境.5名实验者(2女, 3男)轮流在3个环境中进行了为期两周的活动, 包含吃饭、洗碗、穿衣服、洗漱这4种原地行为以及睡觉和看电视两种静止行为.在这些行为之间, 实验者可以自由走动, 进行不同行为间的切换, 且对实验者的行走时间、行走路线未作任何要求.每个环境中, 在实验者知情的情况下, 布置了摄像头用于记录真实的活动情况.整个实验过程中, 一共采集了5 000段行走行为, 其中65%的行走在开始或结束包含原地行为, 35%的行走在开始和结束仅连接着静止行为.具体地, 我们采用以下两个指标来评估行走识别的性能:
| $Presion = \frac{{TruePositive}}{{TruePositive + FalsePositive}}, FNR = \frac{{FalseNegative}}{{TruePositive + FalseNegative}}.$ |
|
Fig. 7 Different environmental setting 图 7 不同实验环境的设置 |
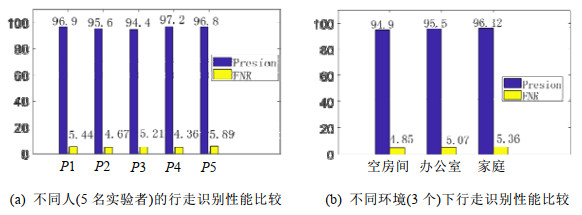
整个实验在不同时间(天)中进行, 实验环境中的家具、收发设备的位置均根据生活需要发生过变化.整体上, 系统行走识别的准确率(presion)为95.5%, 漏报率(FNR)为5.1%.其中, 误报主要是由于一些突然且剧烈的日常行为, 像突然的坐下, 这时身体躯干在短时间内的位移较大, 与行走的位移幅度相似, 所以会造成误报.此外, 漏报常常发生在人转身的时候, 这时由于人在改变行走方向, 所以短时间内的位移较小, 会被判别为原地活动.
不同人的影响: 由于不同人的行走方式、速度会有所差异, 为了证明系统对于不同人的行走依然可以保持一致的识别性能, 本文对比了身高体重不同的5个实验者的准确率和误报率, 如图 8(a)所示.从图中可以看出, 系统对于不同的实验者依然可以保持较好的性能, 准确率均高于94%, 漏报率均低于6%.
|
Fig. 8 图 8 |
不同环境的影响: 为了验证系统在不同的多径环境下的鲁棒性, 本文比较了不同环境的行走识别性能, 如图 8(b)所示.尽管办公室和家庭厨房比空房间的多径环境更复杂, 但是行走识别的性能并没有下降, 表明: 系统在不同的环境下依然可以很稳定地识别出行走行为, 这主要是因为选择的覆盖圆直径大小这一特征来识别行走, 物理含义清晰, 且完全不依赖于多径环境.
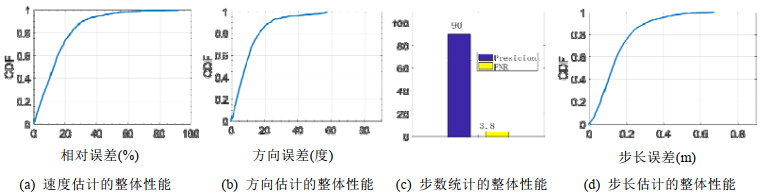
4.3 行走参数估计的性能除了行走的识别, 对行走速度、方向、步数和步长这些参数的精确估计也非常重要.为了计算各个行走参数的估计准确度, 我们需要知道各个参数的Ground truth.特别地, 为了获得人真实的行走速度, 我们在空房间(如图 7(a)所示)和办公室(如图 7(b)所示)中部署了可以实时反映人的位置和速度信息的VR系统HTC Vive; 同时, 在感知区域内的地板上, 分别沿0°、30°、60°、90°、120°、150°这6个不同的角度方向进行了标记, 用于记录真实的行走方向.在实验者知情的情况下, 环境中布置了摄像头, 用于记录实验者真实行走的步数.行走步长的Ground truth则是通过结合摄像头中获取的行走步数和HTC Vive获取的行走距离计算出来.实验时, 实验者胸上佩戴VR手柄, 多次沿不同角度的标记行走, 并由系统估计其行走的速度大小、方向, 统计其行走的步数和步长.为了估计行走参数, 我们在空屋子和办公室两个环境中一共收集了3名实验者(1名男性, 两名女性)共1 000次行走数据.图 9展示了系统行走参数估计的整体性能.具体地, 行走速度大小的相对中位误差为12.2%, 行走方向的中位误差为9°, 行走计步的准确率为90%, 漏报率为3.8%, 步长估计的中位误差为0.12m.
|
Fig. 9 Overall estimation performance of walking parameters 图 9 行走参数估计的整体性能 |
不同行走速度的影响: 由于人行走速度会有所差异, 系统同时考虑了不同行走速度的影响.考虑到大多数人的行走速度在1m/s~1.5m/s之间[38, 39], 为了充分证明系统的鲁棒性, 我们在3种行走速度下, 验证了行走参数估计的性能: 中速(normal: 1m/s~1.5m/s)、慢速(slow: 0.8m/s~1m/s)、快速(fast: 1.5m/s~3m/s), 然后由一名实验者以3种速度进行了多次行走.如图 10(a)和图 10(b)所示: 在不同的行走速度下, 行走速度和方向估计的误差相似, 所以不同的行走速度并不影响系统对行走速度和方向的估计.而对于步数的统计, 如图 10(c)所示: 随着人行走速度的增大, 步数统计的准确率逐渐降低.这是由于, 当人以飞快的速度行走时, 其加速和减速的过程也变快且不明显, 每一步引起的速度变化也更加不容易被观察到.其中, 对于正常或慢速的行走, 步数统计的精度均高于90%;当人飞快行走时, 步数统计的精度虽然有所下降, 但依然高于88%.同样, 对于正常或慢速行走, 步长估计的中位误差要低于快速行走时的中位误差.这是因为, 系统对于步长的估计依赖于步数的统计, 所以当步数统计性能下降时, 步长估计的精度也会受到影响.
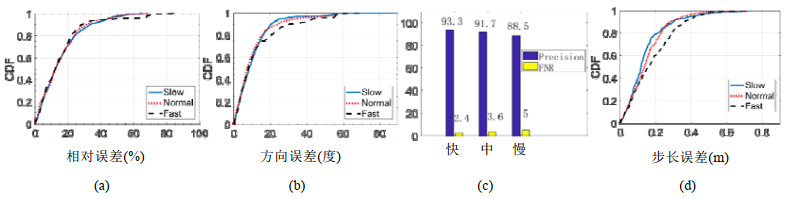
|
Fig. 10 Estimation performance of walking speed, walking direction and walking steps when the volunteer walks in different speed 图 10 不同行走速度下, 行走方向估计、行走速度和行走步数估计的性能比较 |
不同行走方向的影响: 系统同样考虑了人沿不同方向行走时对行走参数估计的影响.如图 11所示: 当人沿不同方向行走时, 行走速度、方向、步数和步长估计并无明显差异, 进一步证明了系统的鲁棒性.
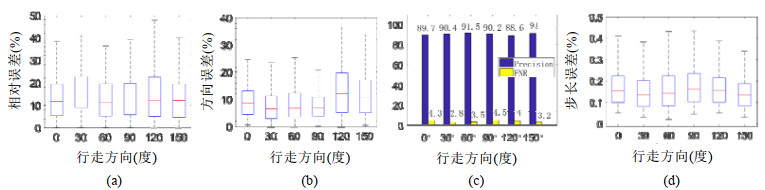
|
(a) 不同行走方向对行走速度估计的影响; (b) 不同行走方向对行走方向估计的影响; (c) 不同行走方向对行走步数估计的影响; (d) 不同行走方向对行走步长估计的影响 Fig. 11 Estimation performance of walking speed, walking direction, walking steps and stride length when the volunteer walks in different direction 图 11 不同行走方向下, 行走方向、行走速度、行走步数和行走步长估计的性能比较 |
不同人的影响: 由于不同人的行走方式存在差异, 我们比较了身高、体重不同的3名实验者(1名男性, 2名女性)对行走参数估计的影响.如图 12所示, 行走参数估计的性能对于不同人保持了较好的一致性.
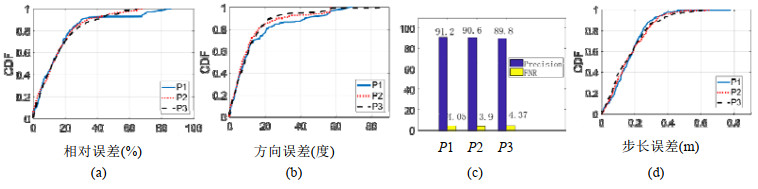
|
(a) 不同人对行走速度估计的影响; (b) 不同人对行走方向估计的影响; (c) 不同人对行走步数估计的影响; (d) 不同人对行走步长估计的影响 Fig. 12 Estimation performance of walking speed, walking direction and walking steps for different people 图 12 不同人在行走时, 行走方向估计、行走速度和行走步数估计的性能比较 |
不同环境的影响: 除此之外, 我们比较了空屋子和办公室两个不同多径环境中的行走参数估计的性能, 如图 13所示.由于本文提出的基于多普勒速度的行走参数估计方法完全不依赖于环境, 所以环境的改变并不会影响行走参数估计的性能.
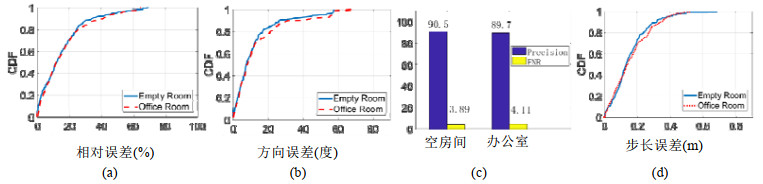
|
(a) 不同环境对行走速度估计的影响; (b) 不同环境对行走方向估计的影响; (c) 不同环境对行走步数估计的影响; (d) 不同环境对行走步长估计的影响 Fig. 13 Estimation performance of walking speed, walking direction and walking steps in different environments 图 13 不同环境下, 行走方向估计、行走速度和行走步数估计的性能比较 |
5 总结
行走是日常生活中最常见的行为之一, 它的状态可以反映人的身份、健康等重要信息, 而行走的速度、方向和步数等细粒度的信息可以为室内追踪、步态分析、老人看护等情境感知场景提供重要参考.随着Wi-Fi技术的兴起, 基于Wi-Fi的行走行为感知受到了研究人员的广泛关注.为了从Wi-Fi信号中提取出反映人行走信息的信号特征, 当前的行走识别和行走参数估计方法主要依赖于大量的经验观察, 所提取的信号波动性、时域相关性等特征与行为间的映射关系较为间接; 且由于缺乏理论指导, 凭经验观察提取的特征中往往包含与环境和感知目标相关的多余信息, 造成系统学习成本高, 对走动方式的限制较大, 系统鲁棒性较差.不同于以往工作, 本文通过分析人在行走过程中产生的多普勒效应和Wi-Fi信道状态信息之间的关系, 建立了基本的多普勒速度运动模型, 进一步通过多重信号分离(MUSIC)算法, 从信道状态信息中获得了可以反映人运动状态的多普勒速度.最后, 通过揭示多普勒速度和人行走的真实速度之间的映射关系, 实现了基于多普勒速度的行走识别和细粒度的行走参数估计.为了验证行走识别和行走参数估计方法的有效性和鲁棒性, 本文从不同人、不同环境、不同行走速度、不同行走方向等多个角度进行了大量的实验.其中, 系统的行走识别准确率达到95.5%, 行走速度大小估计的相对中位误差为12.2%, 方向估计误差为9°, 行走计步的准确率为90%.本文首次在不需要任何学习的情况下, 实现了在连续活动中行走行为的精准识别, 并且能够同时精确地估计行走的速度、方向和步数等多维基本信息, 为上层情境感知应用提供服务.
未来, 基于Wi-Fi的无接触感知技术将在智慧家庭、智能看护中扮演着重要的角色, 且由于其不要求感知目标携带任何设备, 所以非常适合进行长期的感知和看护.通过长期对老年人行走行为进行识别, 可以推测老年人的生活习惯、健康状况, 也有助于及时发现异常.例如: 被看护的老年人一天内的行走时间突然大大减少, 或者出现深夜行走活动, 可能需要及时对老年人的身体健康进行关注.除了行走识别, 结合细粒度的行走参数信息, 一方面可以辅助当前粗粒度的无接触室内定位技术, 提高室内定位的精度; 另一方面, 也可以基于这些底层信息分析更高层次的步态信息, 进行身份识别、身体健康判别、疾病推测等.像患有阿尔兹海默症的老年人, 其早期症状主要体现在行走方式上会发生变化, 而这些症状往往很难被短时间观察到.通过对行走参数的长时间估计, 有助于医生进行参考, 做出合理的判断并提前采取治疗措施.当然, 将行走状态的监测与医疗、智慧家庭等领域相结合, 在实际中必然充满着挑战, 但却是具有价值且有趣的课题, 值得作为未来的研究方向去深入探讨.
| [1] |
Hardegger M, Roggen D, Troster G. 3D ActionSLAM: Wearable person tracking in multi-floor environments. Personal and Ubiquitous Computing, 2015, 19(1): 123-141.
[doi:10.1007/s00779-014-0815-y] |
| [2] |
Yun X, Calusdian J, Bachmann ER, McGhee RB. Estimation of human foot motion during normal walking using inertial and magnetic sensor measurements. IEEE Tran. on Instrumentation & Measurement, 2012, 61(7): 2059-2072.
[doi:10.1109/TIM.2011.2179830] |
| [3] |
Hamilton JM, Joyce BS, Kasarda ME, Tarazaga PA. Characterization of human motion through floor vibration. In: Proc. of the 32nd IMAC Dynamics of Civil Structures. Cham: Springer-Verlag, 2014.63-170. http://doi.org/10.1007/978-3-319-04546-7__19
|
| [4] |
Schuller B, Pokorny F, Ladsatter S, Fellner M, Graf F, Paletta L. Acoustic geo-sensing: Recognising cyclists' route, route direction, and route progress from cell-phone audio. In: Proc. of the Int'l Conf. on Acoustics, Speech and Signal Processing. Vancouver: IEEE, 2013.453-457. http://doi.org/10.1109/ICASSP.2013.6637688
|
| [5] |
Eldib M, Deboeverie F, Philips W, Aghajan H. Behavior analysis for elderly care using a network of low-resolution visual sensors. Journal of Electronic Imaging, 2016, 25(4): 1-17.
[doi:10.1117/1.JEI.25.4.041003] |
| [6] |
Ohnishi K, Kanehira A, Kanezaki A, Harada T. Recognizing activities of daily living with a wrist-mounted camera. In: Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016.3103-3111. https://doi.org/10.1109/CVPR.2016.338
|
| [7] |
Wang Y, Liu J, Chen Y, Gruteser M, Yang J, Liu HB. E-Eyes: Device-free location-oriented activity identification using fine-grained WiFi signatures. In: Proc. of the 20th Annual Int'l Conf. on Mobile Computing and Networking. Hawaii: ACM, 2014.617-628. https://doi.org/10.1145/2639108.2639143
|
| [8] |
Wange W, Liu AX, Shahzad M, Ling K, Lu S. Understanding and modeling of Wi-Fi signal based human activity recognition. In: Proc. of the 21st Annual Int'l Conf. on Mobile Computing and Networking. Paris: ACM, 2015.65-76. https://doi.org/10.1145/2789168.2790093
|
| [9] |
Wang W, Liu AX, Shahzad M. Gait recognition using WiFi signals. In: Proc. of the 2016 ACM Int'l Joint Conf. on Pervasive and Ubiquitous Computing. Heidelberg: ACM, 2016.363-373. https://doi.org/10.1145/2971648.2971670
|
| [10] |
Zeng Y, Pathak PH, Mohapatra P. WiWho: WiFi-based person identification in smart spaces. In: Proc. of the 15th Int'l Conf. on Information Processing in Sensor Networks. Vienna: IEEE, 2016.1-12. https://doi.org/10.1109/IPSN.2016.7460727
|
| [11] |
Wu D, Zhang DQ, Xu CR, Wang YS, Wang H. WiDir: Walking direction estimation using wireless signals. In: Proc. of the 2016 ACM Int'l Joint Conf. on Pervasive and Ubiquitous Computing. Heidelberg: ACM, 2016.351-362. https://doi.org/10.1145/2971648.2971658
|
| [12] |
Xu Y, Yang W, Wang JX, Zhou X, Li H, H LS. WiStep: Device-free step counting with WiFi signals. In: Proc of the ACM on Interactive, Mobile, Wearable and Ubiquitous Technologies. New York: ACM, 2018.1-23. https://doi.org/10.1145/3178157
|
| [13] |
Hsu CY, Liu YC, Kabelac Z, Hristov R, Katabi D, Liu C. Extracting gait velocity and stride length from surrounding radio signals. In: Proc. of the 2017 CHI Conf. on Human Factors in Computing Systems. Denver: ACM, 2017.2116-2126. https://doi.org/10.1145/3025453.3025937
|
| [14] |
Li SJ, Li X, Niu K, Wang H, Zhang Y, Zhang DQ. AR-alarm: An adaptive and robust intrusion detection system leveraging CSI from commodity Wi-Fi. In: Proc. of the 2017 Int'l Conf. on Smart Homes and Health Telematics. Cham: Springer-Verlag, 2017.211-223. https://doi.org/10.1007/978-3-319-66188-9_18
|
| [15] |
Xiao J, Wu KS, Yi YW, Wang L, Ni LM. FIMD: Fine-grained device-free motion detection. In: Proc. of the 18th Int'l Conf. on Parallel and Distributed Systems. Singapore: IEEE, 2012.229-235. https://doi.org/10.1109/ICPADS.2012.40
|
| [16] |
Qian K, Wu CS, Yang Z, Liu YH, Zhou ZM. PADS: Passive detection of moving targets with dynamic speed using PHY layer information. In: Proc. of the 18th Int'l Conf. on Parallel and Distributed Systems. IEEE, 2014.1-8. https://doi.org/10.1109/PADSW.2014.7097784
|
| [17] |
Wu CS, Yang Z, Zhou ZM, Liu XF, Liu YH, Cao JN. Non-invasive detection of moving and stationary human with Wi-Fi. IEEE Journal on Selected Areas in Communications, 2015, 33(11): 2329-2342.
[doi:10.1109/JSAC.2015.2430294] |
| [18] |
Wang J, Jiang HB, Xiong J, Jamieson K, Chen XJ, Fang DY, Xie BB. LiFS: Low human-effort, device-free localization with fine-grained subcarrier information. In: Proc. of the 22nd Annual Int'l Conf. on Mobile Computing and Networking. New York: ACM, 2016.243-256. https://doi.org/10.1145/2973750.2973776
|
| [19] |
Li X, Li SJ, Zhang DQ, Xiong J, Wang YS, Mei H. Dynamic-MUSIC: Accurate device-free indoor localization. In: Proc. of the 2016 ACM Int'l Joint Conf. on Pervasive and Ubiquitous Computing. New York: ACM, 2016.196-207. https://doi.org/10.1145/2971648.2971665
|
| [20] |
Li X, Zhang DQ, Lv Q, Xiong J, Li SJ, Zhang Y, Mei H. IndoTrack: Device-free indoor human tracking with commodity Wi-Fi. In: Proc. of the ACM on Interactive, Mobile, Wearable and Ubiquitous Technologies. New York: ACM, 2017.1-22. https://doi.org/10.1145/3130940
|
| [21] |
Qian K, Wu CS, Yang Z, Liu YH, Jamieson K. WiDar: Decimeter-level passive tracking via velocity monitoring with commodity Wi-Fi. In: Proc. of the 18th ACM Int'l Symp. on Mobile Ad Hoc Networking and Computing. Chennai, 2017.1-10. https://doi.org/10.1145/3084041.3084067
|
| [22] |
Qian K, Wu CS, Zhang Y, Zhang Y, Zhang GD, Yang Z, Liu YH. Widar2.0: Passive human tracking with a single Wi-Fi link. In: Proc. of 16th ACM Int'l Conf. on Mobile Systems, Applications, and Services. Munich: ACM, 2018.350-361. https://doi.org/10.1145/3210240.3210314
|
| [23] |
Ali K, Liu AX, Wang W, Shahzad M. Keystroke recognition using Wi-Fi signals. In: Proc. of the 21st Annual Int'l Conf. on Mobile Computing and Networking. Paris: ACM, 2015.90-102. https://doi.org/10.1145/2789168.2790109
|
| [24] |
Li H, Yang W, Wang JX, Xu Y, Huang LS. WiFinger: Talk to your smart devices with finger-grained gesture. In: Proc. of the 2016 ACM Int'l Joint Conf. on Pervasive and Ubiquitous Computing. Heidelberg: ACM, 2016.250-261. https://doi.org/10.1145/2971648
|
| [25] |
Wang GH, Zou YP, Zhou ZM, Wu KS, Ni LM. We can hear you with Wi-Fi!. IEEE Trans. on Mobile Computing, 2016, 15(11): 2907-2920.
[doi:10.1145/2639108.2639112] |
| [26] |
Zhang DQ, Wang H, Wu D. Toward centimeter-scale human activity sensing with Wi-Fi signals. IEEE Computer Magazine, 2017, 50(1): 48-57.
[doi:10.1109/MC.2017.7] |
| [27] |
Wang H, Zhang DQ, Ma JY, Wang YS, Wang YX, Wu D, Gu T, Xie B. Human respiration detection with commodity Wi-Fi devices: Do user location and body orientation matter? In: Proc. of the 2016 ACM Int'l Joint Conf. on Pervasive and Ubiquitous Computing. Heidelberg: ACM, 2016.25-36. https://doi.org/10.1145/2971648
|
| [28] |
Zhang FS, Zhang DQ, Xiong J, Wang H, Niu K, Jin BH, Wang YX. From Fresnel diffraction model to fine-grained human respiration sensing with commodity Wi-Fi devices. In: Proc. of the ACM on Interactive, Mobile, Wearable and Ubiquitous Technologies. Singapore: ACM, 2018.1-23. https://doi.org/0000001.0000001
|
| [29] |
Wu D, Zhang DQ, Xu CR, Wang H, Li X. Device-free Wi-Fi human sensing: From pattern-based to model-based approaches. IEEE Communications Magazine, 2017, 55(10): 91-97.
[doi:10.1109/MCOM.2017.1700143] |
| [30] |
Liu J, Wang Y, Chen YY, Yang J, Chen X, Chen J. Tracking vital signs during sleep leveraging off-the-shelf Wi-Fi. In: Proc. of the 16th ACM Int'l Symp. on Mobile Ad Hoc Networking and Computing. New York: ACM, 2015.267-276. https://doi.org/10.1145/274628
|
| [31] |
Han CM, Wu KS, Wang YX, Ni LM. WiFall: Device-free fall detection by wireless networks. In: Proc. of the 2014 IEEE Conf. on Computer Communications. Toronto: IEEE, 2014.271-279. https://doi.org/10.1109/INFOCOM.2014.6847948
|
| [32] |
Wang H, Zhang DQ, Wang YS, Ma JY, Wang YX, Li SJ. RT-fall: A real-time and contactless fall detection system with commodity WiFi devices. IEEE Trans. on Mobile Computing, 2017, 16(2): 511-526.
[doi:10.1109/TMC.2016.2557795] |
| [33] |
Li SJ, Li X, Lv Q, Tian GY, Zhang DQ. Wi-Fit: Ubiquitous bodyweight exercise monitoring with commodity Wi-Fi devices. In: Proc. of the 15th IEEE Int'l Conf. on Ubiquitous Intelligence and Computing. Guangzhou: IEEE, 2018.530-537. https://doi.org/10.1109/SmartWorld.2018.00114
|
| [34] |
Wang YX, Li SJ, Wang H, Ma JY, Wang YS, Zhang DQ. Survey on Wi-Fi based contactless activity recognition. Jounal of Zhejiang University (Engineering Science), 2017, 5(4): 648-654(in Chinese with English abstract).
https://www.cnki.com.cn/Article/CJFDTOTAL-ZDZC201704002.htm |
| [35] |
Li X. Wi-Fi-based passive sensing based on the target reflected signal's parameters estimation[Ph. D. Thesis]. Beijing: Peking University, 2018(in Chinese with English abstract).
|
| [36] |
Zhang DQ, Wang H, Wu D. Toward militimeter-scale contactless sensing with Wi-Fi signals: From pattern to model. Communications of China Computer Federation, 2018, 14(1): 18-26(in Chinese with English abstract).
|
| [37] |
Halperin D, Hu WJ, Sheth A, Wetherall D. Tool release: Gathering 802.11N traces with channel state information. SIGCOMM Computer Communator, 2011, 41(1): 53-53.
[doi:10.1145/1925861.1925870] |
| [38] |
Fritz SL, Lusardi M. White paper: Walking speed: The sixth vital sign. Journal of Geriatric Physical Therapy, 2009, 32(2): 46.
http://c.ymcdn.com/sites/www.fpta.org/resource/collection/36352F1F-0CB4-4BB3-8A88-80F959C8DED4/Walking_Speed__the_Sixth_Vital_Sign_2009.pdf |
| [39] |
Bohannon WR. Comfortable and maximum walking speed of adults aged 20~79 years: Reference values and determinants. Age and Ageing, 1997, 26(1): 15.
[doi:10.1093/ageing/26.1.15] |
| [34] |
王钰翔, 李晟洁, 王皓, 马钧轶, 王亚沙, 张大庆. 基于Wi-Fi的非接触式行为识别研究综述. 浙江大学学报(工学版), 2017, 5(4): 648-654.
https://www.cnki.com.cn/Article/CJFDTOTAL-ZDZC201704002.htm |
| [35] |
李翔. 基于目标反射信号参数估计的Wi-Fi非接触式感知技术[博士学位论文]. 北京: 北京大学, 2018.
|
| [36] |
张大庆, 王皓, 吴丹. 毫米级的Wi-Fi无接触感知: 从模式到模型. 中国计算机学会通讯, 2018, 14(1): 18-26.
|
 2021, Vol. 32
2021, Vol. 32


