2. 计算机科学国家重点实验室(中国科学院 软件研究所), 北京 100190;
3. 中国科学院大学, 北京 100049
2. State Key Laboratory of Computer Science(Institute of Software, The Chinese Academy of Sciences), Beijing 100190, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
随着互联网(Internet)、物联网(IoT)等技术的快速发展,数据(data)开始从简单处理对象向基础性服务转变,多个作业(job)同时提交,分解成并行执行任务(task),在至少万级规模的物理服务器上运行处理,已成主流的应用模式,学术界称为并行作业(concurrent job)[1]问题.例如,Github每年需处理2 000多万个作业[2],Facebook每天要响应近万个作业请求[3].
大规模资源调度是指决策任务与物理资源映射关系的过程,它是解决并行作业问题的关键.已有的研究工作或权衡任务干扰约束(cross-task interference)和资源利用率(high resource utilization),如Whare-Map[4],Tetrisched[5];或权衡公平性(fairness)和数据局部性(data locality),如Quincy[6],YARN[7];或权衡公平性(fairness)和隔离性(isolation),如Mesos[8],Omega[9];或满足优先级(priority)等单一约束条件,如Borg[3],Alsched[10],Quasar[11].上述研究均假设决策目标固定不变,但相关研究表明:相同的作业集合采用固定的调度决策算法,或导致极低的资源利用率,如Twitter平均资源利用率小于20%[11];或引起作业性能下降80%[8],如任务未绑定特殊硬件进行加速,违反优先级约束.因此,如何提高大规模资源调度的灵活性,使其具备按需配置能力,正逐渐引起工业界和学术界的广泛关注,面临巨大挑战.所谓灵活性,是指调度系统支持多种调度目标,且可针对不同场景需求,灵活选取最优调度目标以适应需求.例如典型的电商场景,商品的推荐任务关注时效性,应优先处理;涉及商品的各种统计任务则强调公平性,需平分资源[6].
本文首先对相关工作进行总结,归纳出3种典型的度量指标,接着分析基于队列(queueing)的大规模资源调度模型,举例说明队列模型灵活性不足,难以支持多种调度场景,无法按需配置生效,其本质原因是该模型表达能力不足,且仅能满足局部最优解.然后,基于最小费用最大流图对大规模资源调度建模,将满足3种典型度量的资源调度方法映射为图的构造问题.最后,采用增量方法降低图的求解复杂度.通过实测和仿真两个方面,验证了本方法的有效性.
本文的主要贡献是:提出了基于最小费用最大流的大规模资源调度方法,将资源调度问题转换成最小费用最大流图的构造和求解问题;总结相关工作,从公平性、优先级和放置约束这3种典型度量入手,将调度目标映射为图的构造问题,并通过改变图的结构使其具备适应性调整能力,支持按需配置;图的求解过程本质是资源调度决策过程,快速决策是方法实用性前提.本文针对图的求解时间复杂度高的问题,实现了一种增量式优化算法;实现原型系统,通过实测验证本方法的灵活性,可应对真实场景下按需配置调度目标的需求,且调度延迟几乎与队列模型相当,可适应万级规模的资源调度场景.
本文第1节是相关工作介绍和总结.第2节是问题描述和研究思路,分析队列模型灵活性不足的原因,提出基于最小费用最大流的资源调度建模方法.第3节介绍采用最小费用最大流的求解过程,核心是图的构造和求解方法.第4节从实测和仿真两个方面验证本方法的有效性.最后总结本文工作,并展望未来的研究方向.
1 相关工作大规模资源调度是近年来学术界研究热点,根据度量指标的不同,大致可以分为3类.
· 面向公平性的资源调度方法
Delay-Schedule[12]采用队列模型,主要权衡任务调度公平性和数据局部性,针对已有贪心算法难以计算全局最优解的不足,设计了“匹配-调度”和“不匹配-超时等待-重调度”机制;Sparrow[13]采用队列模型,提出了一种基于采样的资源调度方法,根据历史运行数据不断修正调度策略,其目的是兼顾公平性和数据局部性;Mesos[8]实现一种面向异构任务的资源调度框架,主要考虑任务公平性需求,采用两级队列模型,任务只允许在分配的资源上运行;Quincy[6]将任务资源需求和物理资源供给转变为最小费用流图问题,通过费用的调整达到权衡任务公平性和数据局部性目标.Choosy[14]将Max-Min算法应用到队列模型,提出了一种资源公平调度方法.
· 面向优先级的资源调度方法
Borg[3]采用队列模型,主要考虑任务的优先级特性,设计了任务排序算法和低优先级任务置换机制; Omega[9]是Borg工作的扩展,主要解决任务调度优先级和任务运行干扰之间的矛盾;Quasar[11]面向异构物理资源场景,提出了一种基于分类的资源调度方法,建立了一套任务和资源匹配的评估模型,优先将应用调度到合适的物理资源上,并尽量避免任务干扰;KMN[15]主要针对数据密集型场景,基于DAG模型刻画出任务之间的关联关系,并优先将相关任务调度到网络延迟较小的物理节点上;Apollo[16]提出了一种基于长作业优先的资源调度方法,尽量提高全局资源利用率.
· 面向放置约束的资源调度方法
Alsched[10]采用队列模型,将任务需满足的资源约束(比如GPU亲和性)刻画成收益,提出了一种基于效用的资源调度方法,用于评估任务放置在不同物理资源上的收益;Tetrisched[17]扩展了Alsched,主要贡献是通过对运行时数据分析,挖掘任务之间关联关系,并将其刻画成收益;Bistro[18]实现了一种面向在线和离线任务的资源调度框架,基于队列模型,采用两级调度机制和重配置机制,确保离线任务运行在指定的资源范围;Paragon[19]提出了一种基于多队列和分类的资源调度方法,考虑到异构资源供给能力的差异、异构应用的资源需求差异,自动构建资源收益评估函数.
综上所述,已有的研究目标主要包括公平性、优先级和放置约束这3类,通常以上述目标为主线,根据实际应用场景,或采用队列模型,权衡资源利用率、数据局部性等其他属性,以达到局部最优解目的;或采用图模型,主要关注图的费用赋值问题,仅能适用固定目标的全局最优解.本方法扩展图的表达能力,采用最小费用最大流网络,将上述3种典型调度目标通过资源视角进行描述,并将问题映射到图的问题和求解问题.
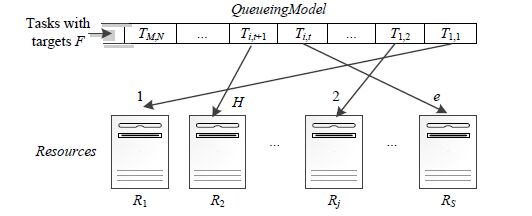
2 问题分析和研究思路 2.1 问题分析图 1是基于队列的资源调度模型,并行作业问题可表述为任务资源需求与物理资源供给的最优匹配问题C:TxR=t2,其中,T={T1,1,T1,2,…,Ti,t,Ti,t+1,…,TM,N}表示
|
Fig. 1 Queue-Based scheduling model 图 1 基于队列的调度模型 |
| Table 1 Detailed descriptions for element in queue-based scheduling model 表 1 基于队列的资源调度模型元素说明 |
假设:
1) 数据本地性(data locality)为调度目标,通过函数E(T)={R1,…,Rw}刻画任务T与物理资源R的最优匹配期望集合,预设定以下约束条件.
· E(T1,1)={R1,R2}表示任务T1,1期望调度到物理资源R1,R2上为最优解;
· E(T1,2)={R1,RS}表示任务T1,2期望调度到物理资源R1上为最优解;
· E(Ti,t)={Rj}表示任务Ti,t(1≤i≤M,1≤t≤N)期望调度到物理资源Rj(1≤j≤S)上为最优解.
2) 引入评价指标A(Ti,t)⊆E(Ti,t)(1≤i≤M,1≤t≤N)表示任务调度是否满足预期.如图 1所示,任务T与物理资源R的实际调度结果由函数A(T)={R1,R2,…,Rw}刻画.
· A(T1,1)={R1}表示任务T1,1实际调度到物理资源R1上;
· A(T1,2)={Rj}表示任务T1,2实际调度到物理资源Rj上;
· A(Ti,t)={RS}表示任务Ti,t(1≤i≤M,1≤t≤N)实际调度到物理资源RS上.
根据评价指标可知,仅仅任务T1,1为最优解.Quincy[6]最早阐述了该问题,认为队列模型表达能力受限,如采用FIFO(first input first output)策略,使得T1,1任务在调度时难以统筹考虑T1,2和Ti,t资源需求约束,只能计算局部最优解,难以适用并行作业问题.相对于Quincy,本文的贡献在于:将调度问题转化为图的构造问题,支持灵活性调度;对图的求解进行优化,降低求解时间,适应大规模集群.
2.2 研究思路最小费用最大流问题是经济学和管理学中的一类典型问题,已应用到物资供给、航班衔接等多种并行任务场景,通常采用图模型进行刻画,通过图中路径的容量和费用限制,寻求多个任务的全局最优解.本文将其应用到资源调度场景,假设给定图G=(V,E,U,C),其中:V是节点集,表示资源供需实体,包括任务需求方和资源供给方;E是边集,表示任务与资源的可满足性,即,任务能否映射到相应资源;U是边上容量,表示资源供给能力;C是费用,表示任务与资源的映射效果.
图 2是基于图的最小费用最大流问题建模,左侧是任务集合T,右侧是物理资源集合M,边T1,2→M1以及T2,1→U1表示资源M1和U1为任务T1,2资源供给的候选项;每条边的容量和费用表示任务是否可调度到相应物理资源上(容量),如果可以,其供给的效果(费用)如何.资源调度问题映射到最小费用最大流问题后,图中各元素的物理含义见表 2(A→B表示A到B节点构成的有向边,*号表示任意节点),其难点是图的构造和求解问题.

|
Fig. 2 Minimum cost maximum flow scheduling model 图 2 最小费用最大流网络调度模型 |
| Table 2 Details descriptions fro element in minimum cost maximum flow scheduling model 表 2 基于最小费用最大流调度元素具体含义 |
1) 3种典型资源调度目标如何映射到图构造问题,通过改变图的样式使资源调度具有灵活性;
2) 图的求解时间复杂度远远高于队列模型,如何进行决策优化,提高其实用性.
3 图的构造和求解问题公平性、放置约束、优先级是资源调度的3种主要度量指标.本节首先介绍如何从资源视角刻画上述调度目标,并将其转换为图的容量和费用赋值问题,接着针对图的求解问题,提出了基于增量式最小费用流算法.
3.1 图的构造问题 3.1.1 公平性Quincy[6],Delay-Schedule[12],Sparrow[13]是典型的公平性研究工作.公平性指作业能够公平共享资源份额(资源份额通过特定公平算法[20]计算得出,如最大最小公平算法).例如,对于Jobj,其包含的任务数为Nj,通过公平算法计算其公平份额为Aj,如果调度算法分配给Jobj的资源份额为Aj,则该调度算法满足公平性.
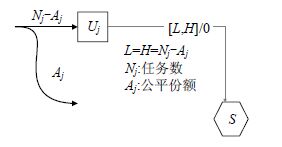
公平性通过图的边容量构造来表达,如图 3所示.
|
Fig. 3 Example of fairness construction 图 3 公平性目标构造示例 |
设置Uj→S容量上下界为
| $[{{N}_{j}}-{{A}_{j}},{{N}_{j}}-{{A}_{j}}]$ | (1) |
由于Uj→S的上下界均为Nj-Aj,则通过Uj的流量fu=Nj-Aj(最小费用最大流网络模型的约束条件)即Jobj中需要等待的任务为Nj-Aj个.Jobj的任务Nj或流向Uj处于等待状态,或流向资源节点进行调度,因此,Jobj通过资源节点的流量:
| ${{f}_{r}}={{N}_{j}}-({{N}_{j}}-{{A}_{j}})={{A}_{j}}$ | (2) |
即Jobj分配到Aj份额资源,满足最大最小公平性.
例如,给定Job1和Job2,分别包含3个任务T1,1~T1,3和4个任务T2,1~T2,4,4台机器M1~M4,每个机器可运行一个任务,每个Job资源需求为2.在对图进行构造时,U1→S容量上下界赋值为[1, 1],U2→S容量上下界赋值为[2, 2],即:Job1有一个任务等待,Job2有两个任务等待,对应Job1有两个任务占用两台机器运行,Job2有两个任务占有两台机器运行,满足公平性.
3.1.2 放置约束Alsched[10],Quasar[12],etrisched[21]是典型的放置约束研究工作,放置约束可描述为如下三元组:
| $placement constraint=\left\langle task,resources,utility \right\rangle $ | (3) |
其中,Task表示任务;resources表示任务约束的资源,表示task放置到resources上所获得的效益.采用效益函数描述放置约束,即:
| $\max \sum{utility}$ | (4) |
放置约束可映射到图的边有无构造问题.
在task和resources之间建立一条边task→resources,并赋予一个与效益值相反的费用,即:
| $cost(task\to resource)=-utility$ | (5) |
最大效益函数对应最小费用:
| $\min \sum{cost}$ | (6) |
由公式(4) 、公式(6) 可知,通过最小费用最大流网络表述的放置约束等价于放置约束的定义.
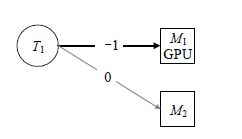
如图 4所示为防止约束构造示例,任务T1图像处理程序,两台机器M1,M2.M1带有GPU,M2无GPU.T1对M1有放置约束,获得的收益为1;对M2无放置约束,即收益为0.通过最小费用最大流求解,可以获得最小费用,即最大收益,T1会在M1执行.
|
Fig. 4 Example of placement constraint construction 图 4 放置约束目标构造示例 |
3.1.3 优先级
Brog[3],KMN[15]是典型的优先级调度研究工作,支持严格优先级,优先级高的任务会先获得资源.
最小费用最大流网络能够通过费用构造来支持优先级调度.
类似Brog,带有优先级调度的费用计算公式定义为
| $cost(u,v)=[{{w}_{1}},{{w}_{2}},...,{{w}_{n}}]\times \left[ \begin{matrix} Priority \\ CPU \\ \vdots \\ {{d}_{n}} \\ \end{matrix} \right]$ | (7) |
其中,w1~wn代表每一维度(优先级维度、CPU利用率维度、磁盘利用率维度等)的权重,每一维度的取值范围规范化为[0,w],w是一个常数值.
· 为满足严格优先级约束,把优先级维度权重赋值
· 对图进行构造时任务相关费用α赋值为cost(u,v).
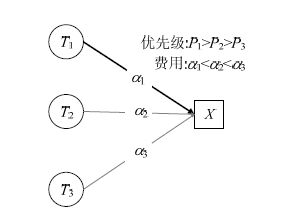
如图 5所示是一个优先级构造示例,3个任务T1,T2,T3优先级为1,2,5,即:T1优先级最高,T2次之,T3优先级最低.根据公式(7) 计算得出所需费用分别为α1,α2,α3,则α1,α2,α3满足α1<α2<α3.假设只有一台机器M,构造最小费用最大流图时,根据最小费用最大流算法最小费用约束,T1会获得资源,T2,T3等待.
|
Fig. 5 Example of priority construction 图 5 优先级目标构造示例 |
3.2 图的求解问题
最小费最大流问题的形式化描述如下.
· 目标函数:
| $\min \sum\nolimits_{(w,v)\in E}{c(w,v)f(w,v)}$ | (8) |
· 约束条件:
| $0\le f\left( w,v \right)\le u\left( w,v \right),\forall \left( w,v \right)\in E$ | (9) |
| $\sum\nolimits_{(w,v)\in E}{f(w,v)-}\sum\nolimits_{(v,w)\in E}{f(v,w)}=b(v),\forall w\in V$ | (10) |
其中,w,v表示图中节点,c(w,v)表示边(w,v)的费用,f(w,v)表示边(w,v)的流量,u(w,v)表示边(w,v)的容量,b(v)>0的顶点为源节点,b(v)<0的点为汇聚节点.满足
当最小费用最大流问题的可行流f满足以下条件之一时,可行流f是最优的.
· 负圈最优化条件(Negative cycle optimality):G(f)中没有费用为负数的增广圈;
· 相对费用最优化条件(Reduced cost optimality):G(f)中每一个边的相对费用cπ(v,w)均大于0;
· 互补松弛最优化条件(complementary slackness optimality):G(f)的边,或满足cπ(v,w)>0且f(v,w)=0,或满足0<f(v,w)<u(v,w)且cπ(v,w)=0,或满足cπ(v,w)<0且f(v,w)=u(v,w).
最小费用最大流求解算法已被广泛实践,其核心思想是:在满足公式(8) ~公式(10) 的前提下,或维护最大流,不断迭代寻找最小费用;或维护最小费用,不断迭代寻找最大流,直到满足最优化条件,可在多项式时间内解决.
Cost scaling[21]和Network simplex[22]是两类典型算法实现,大规模资源调度建模后是稀疏图结构[6],Cost scaling算法对于求解稀疏图性能更优,但Cost scaling算法在10万台物理资源规模下[3]调度延迟仍会大于90s.通过分析与实测Google公开的生产数据集[25]发现,通常图的结构变化较小,因此本文提出一种增量式图求解方法ICS(incremental cost scaling),通过缓存和复用上次求解结果,仅需对图进行局部运算,即可得到图的全局最优解.第4.3.1节的实验结果验证了ICS的有效性和适用性.
对于图G=(V,E,U,C),其最小费用流为f,G网络结构局部发生改变,改变后的图G'=(V',E',U',C').增量式最小费用流算法,即图G'基于G的最小费用流f进一步优化,求得G'的最小费用流f',ICS伪代码见表 3.
| Table 3 Algorithm of incremental minimum cost max flow scheduling 表 3 增量式最小费用最大流算法 |
算法的第3行~第7行基于事件驱动模型循环检全局物理资源的状态改变事件(任务提交、机器宕机等),当有事件发生,更新图的结构,然后复用上次求解结果,调用Cost scaling算法对更新后的图进行求解.第10行~第16行是Cost scaling算法主体,主要思想是缓存并复用上次求解的结果进行迭代,其中,ε表示松弛条件.随着迭代次数增加逐渐减小,f表示初始最大流,基于流f,Cost Scaling算法迭代寻找减小费用条件并更新总费用,直到满足松弛条件ε为止.第17行~第24行是增量迭代操作,采用推送-重标签算法[23]对松弛条件进行更新.增量式算法的时间复杂度和图改变的范围相关,最好情况下为O(VE);最坏条件下需遍历整个图,时间复杂度为O(V2Elog(VC)).
4 实验及结果分析本节主要验证方法的灵活性,可支持多种调度目标,具有按需配置能力,本方法相应的系统实现为Sirius.首先是实验环境介绍,它是验证本方法有效性前提;其次是方法灵活性验证,选择公平性、优先级和约束性这3种典型调度目标的代表性工作,使用文中评价方法与本方法对比,验证本方法是否具备相同的能力;最后是方法调度延迟和资源开销验证,验证本方法是否适应至少万级规模资源调度场景.
4.1 实验环境与负载介绍 4.1.1 实验环境实验环境包括实测环境和仿真环境,物理环境验证Sirius的灵活性,即Sirius支持的调度目标是否和现有开源系统性能相当;仿真环境验证Sirius开销,即Sirius在大规模环境下资源消耗与调度延迟.
· 实测环境:图 6给出由20台刀片服务器组成的实测环境,它包括两个机架,每个机架包括10台物理服务器,每台服务器配置均为24cores,2.4GHz Intel Xeon CPU和24G内存,操作系统版本为Centos7,采用Docker作为任务执行容器,Docker版本为1.0.机架1上的10台机器带有GPU,机架2上的机器不带有GPU,机架交换机和集群交换机配置均为千兆;

|
Fig. 6 Experiment test-bed 图 6 实验环境 |
· 仿真环境:选取Google公开的集群数据[24],包括10 000个物理节点,其中每个节点配置为24Core、64G内存、网络10Gbps,构造最小费用最大流网络结构,验证Sirius在大规模资源调度的性能.
4.1.2 评估指标选取Brog[3]作为优先级调度目标的典型工作,选取Quincy[6]作为公平性调度的典型工作,选取Alsched[10]作为放置约束调度的典型工作,选取工作本身的评估方法,验证Sirius是否具有相似的执行效果.
· 资源利用率(resource utilization):系统的CPU和内存资源使用率百分比;
· 任务平均执行时间(mean task runtime):所有任务执行时间的均值(包括等待时间和运行时间);
· 任务平均等待时间(mean task wait time):所有任务等待时间的均值;
· 系统正交化性能(SNP):SNP是ANP(application normalized performance)的几何平均值:
| $ANP={{T}_{physical}}/{{T}_{experiment}}$ | (11) |
其中,Tphysical表示Job的理论运行时间,Texperiment表示Job实际运行时间.SNP越大,说明公平性越好,理想值为1.
4.1.3 工作负载为验证本方法支持多种调度目标,选择Quincy,Alsched,Brog中常用的工作负载,包括批处理负载和服务负载两类,具体见表 4.
| Table 4 Experiment workload 表 4 实验负载 |
4.2 灵活性验证
本节评估Sirius的灵活性,选取Quincy,Alsched,Brog开源实现Firmament[25],Swarm[26],Kubernetes[27]以及经典随机调度Random作为参考对象,调度评估Sirius是否具备相同的能力.
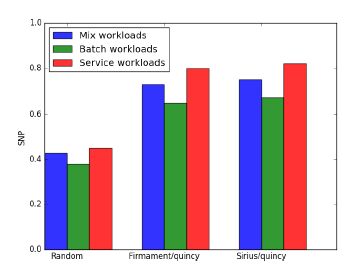
4.2.1 公平性负载选取服务负载和批处理,分别单独运行以及混合运行,评估系统的SNP.Sirius容量K设置为24,与每台机器CPU核数一致,费用采用Quincy配置.
实验结果如图 7所示:在多种负载下,Sirius/quincy和Fimament/quincy的SNP指标接近,且均优于Random,SNP指标约为随机算法的2倍,说明Sirius通过容量控制来满足公平性,如第3.1.1节所示.
|
Fig. 7 SNP of different scheduler 图 7 不同调度器SNP指标 |
4.2.2 放置约束
选取图像分析类负载,修改Sirius容量配置K=1(保证每台机器一个任务).任务数目分为T=10(任务独占GPU)和T=20(任务共享50%GPU),验证Random,Swarm/alsched Sirius/alsched的平均任务执行时间.
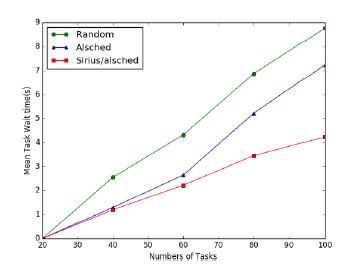
实验结果如图 8所示:在T=10时,Sirius/alsched和Swarm/alsched平均任务执行时间显著优于随机调度决策,约为随机调度的2倍;在T=20时,Sirius/alsched平均任务执行时间优于Swarm/alsched,分析可能是Sirius/ alsched能够更好地权衡任务等待时间.进一步实验,分析3种放置决策在不同任务下的调度延迟,实验结果如图 9所示:随着任务数的增加,Sirius/alsched调度延迟小于Swarm/alsched,与分析结果一致.因此,Sirius支持的Alsched调度决策等价或优于原有系统.

|
Fig. 8 Mean task runtime of different scheduler 图 8 不同调度器平均任务执行时间 |
|
Fig. 9 Mean task wait time of different scheduler 图 9 不同调度器平均任务等待时间 |
4.2.3 优先级
选取3组批处理负载,每组任务数为480(独占CPU内核),分别赋予相同优先级和不同的优先级,Sirius容量K设置为24,验证Kubernetes/brog,Sirius/brog的平均任务执行时间.
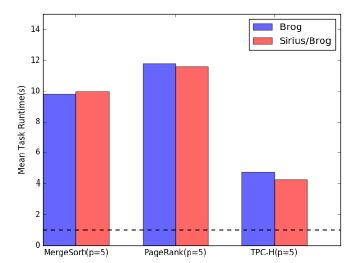
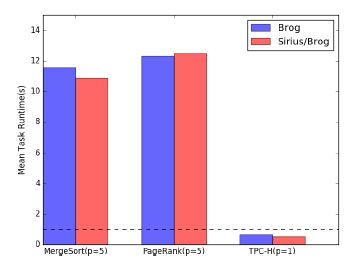
如图 10所示:3种工作负载具有相同的优先级,TPC-H任务延迟大于5s,通常难以满足用户需求.由于在相同优先级下任务平分资源,长任务占用资源不释放,引起短任务饥饿.如图 11所示:将TPC-H任务优先级设置为1,TPC-H任务优先获得资源,查询延迟小于1s,提高5倍.在负载具有相同优先级与不同优先级场景下,Sirius/ brog性能均接近Kubernetes/brog的性能.
|
Fig. 10 Mean task runtime of different scheduling in the same priority workload 图 10 不同调度器、相同优先级负载下的任务执行时间 |
|
Fig. 11 Mean task runtime of different scheduling in different priority workload 图 11 不同调度器不同优先级负载下的平均任务执行时间 |
4.3 调度延迟和资源开销 4.3.1 调度延迟
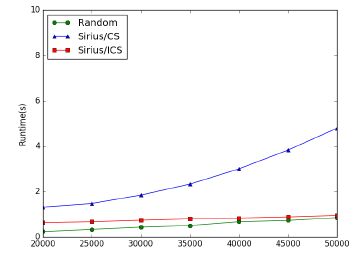
实验采用仿真环境,机器规模选用5 000和10 000两组,负载变化范围从10000~20000(数据来源于Google公开的集群负载[24],评估队列算法Random、非增量算法Cost scaling(CS)、增量算法ICS的运行时间.
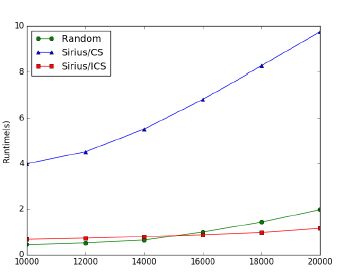
实验结果如图 12和图 13所示:3种算法的运行时间随任务数目增加而增加,近似线性相关,其中,CS算法执延迟远大于增量式算法和队列算法,且随着规模增加,延迟快速增长;队列算法增长速度其次;ICS算法增长速度最慢.当物理服务器规模达到10 000台时,ICS算法性能优于队列算法.此外,ICS算法调度延迟相对于CS算法最多降低10倍.
|
Fig. 12 Runtime of different algorithm in 5 000 simulation node 图 12 5 000个仿真节点下不同算法运行时间 |
|
Fig. 13 Runtime of different algorithm in 10 000 simulation node 图 13 10 000个仿真节点下不同算法运行时间 |
4.3.2 资源开销
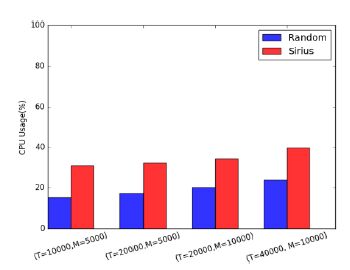
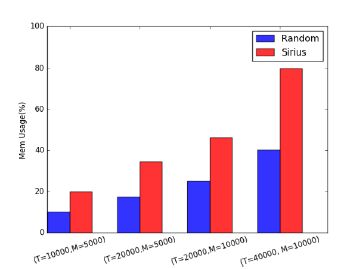
本节评估基于队列的调度系统Random和基于最小费用最大流的调度系统Sirius在不同规模集群下的资源开销,评估指标为CPU使用率和内存使用率.采用Cgroup把Sirius和Random限制到单个CPU核执行,内存大小限制为4GB.
实验结果如图 14和图 15所示:Sirius CPU使用率约为Random的1.5倍,内存使用率约为Random的2倍,且内存使用率随物理资源规模增长不断增大.网络流图的求解本身是CPU敏感型,且增量式求解算法需要缓存上次求解状态,是典型的空间换时间的求解方法,因此,Sirius在CPU和内存方面的资源开销会高于队列模型.我们将在未来的工作中对Sirius进行优化,以减少Sirius的资源消耗.
|
Fig. 14 CPU usage on different size cluster 图 14 不同集群规模下的CPU使用率 |
|
Fig. 15 Memory usage on different size cluster 图 15 不同规模下的内存使用率 |
5 总结与展望
并行作业是大规模资源调度的研究热点.本文提出一种基于最小费用最大流网络的大规模资源调度建模方法,将任务的资源需求和物理资源供给问题转换成最小费用最大流图的构造和求解问题.首先总结相关工作,归纳出公平性、优先级和约束性这3种典型的调度目标;接着从资源的视角,将典型调度目标进行描述,并映射到图的构造问题,使用具备适应性调整能力;然后实现了一种最小费用最大流的增量式求解算法,针对图的求解问题进行优化.目前,该方法还存在如下待改进的问题:首先,费用参数赋值主要依赖人工经验,其取值合理性将严重影响方法的效果,如何实现参数的自动化赋值是后续的主要工作之一;其次,图的求解复杂度高,采用合并、过滤等机制简化图的复杂度,加快资源调度决策时 效性,是该方法在大规模环境中实用的重要前提.我们将继续围绕参数自动化配置和图的求解优化机制展开研究.
| [1] | Black DL. Scheduling support for concurrency and parallelism in the Mach operating system. Computer, 1990, 23(5): 35–43 . [doi:10.1109/2.53353] |
| [2] | Karanasos K, Rao S, Curino C, Douglas C, Chaliparambil K, Fumarola GM, Heddaya S, Ramakrishnan R, Sakalanaga S. Mercury:Hybrid centralized and distributed scheduling in large shared clusters. In:Proc. of the 2015 USENIX Annual Technical Conf. (USENIX ATC 2015), 2015: 485–497 . http://www3.imperial.ac.uk/portal/page/portallive/1771FD684472E7FAE050C69B4739032F |
| [3] | Verma A, Pedrosa L, Korupolu M, Oppenheimer D, Tune E, Wilkes J. Large-Scale cluster management at Google with Borg. In:Proc. of the 10th European Conf. on Computer Systems. ACM Press, 2015. 18.[doi:10.1145/2741948.2741964] |
| [4] | Mars J, Tang L. Whare-Map:Heterogeneity in homogeneous warehouse-scale computers. ACM SIGARCH Computer Architecture News, 2013, 41(3): 619–630 . [doi:10.1145/2485922.2485975] |
| [5] | Tumanov A, Zhu T, Kozuch MA, Harchol-Balter M, Ganger GR. Tetrisched:Space-Time scheduling for heterogeneous datacenters. Technical Report, CMU-PDL-13-112, Carnegie Mellon University, 2013. |
| [6] | Isard M, Prabhakaran V, Currey J, Wieder U, Talwar K, Goldberg A. Quincy:Fair scheduling for distributed computing clusters. In:Proc. of the ACM SIGOPS 22nd Symp. on Operating Systems Principles. ACM Press, 2009. 261-276.[doi:10.1145/1629575.1629601] |
| [7] | Vavilapalli VK, Murthy AC, Douglas C, Agarwal S, Konar M, Evans R, Graves T, Lowe J, Shah H, Seth S, Saha B, Curino C, O'Malley O, Radia S, Reed B, Baldeschwieler E. Apache hadoop yarn:Yet another resource negotiator. In:Proc. of the 4th Annual Symp. on Cloud Computing. ACM Press, 2013.[doi:10.1145/2523616.2523633] |
| [8] | Hindman B, Konwinski A, Zaharia M, Ghodsi A, Joseph AD, Katz R, Shenker S, Stoica I. Mesos:A platform for fine-grained resource sharing in the data center. NSDI, 2011, 11: 22–22 . https://www.usenix.org/node/164444 |
| [9] | Schwarzkopf M, Konwinski A, Abd-El-Malek M, Wilkes J. Omega:Flexible, scalable schedulers for large compute clusters. In:Proc. of the 8th ACM European Conf. on Computer Systems. ACM Press, 2013. 351-364.[doi:10.1145/2465351.2465386] |
| [10] | Tumanov A, Cipar J, Kozuch MA, Ganger GR. Alsched:Algebraic scheduling of mixed workloads in heterogeneous clouds. In:Proc. of the 3rd ACM Symp. on Cloud Computing. ACM Press, 2012.[doi:10.1145/2391229.2391254] |
| [11] | Delimitrou C, Kozyrakis C. Quasar:Resource-Efficient and QoS-aware cluster management. ACM SIGPLAN Notices, 2014, 49(4): 127–144 . [doi:10.1145/2541940.2541941] |
| [12] | Zaharia M, Borthakur D, Sarma SJ, Elmeleegy K, Shenker S, Stoica I. Delay scheduling:A simple technique for achieving locality and fairness in cluster scheduling. In:Proc. of the 5th European Conf. on Computer Systems. ACM Press, 2010. 265-278.[doi:10.1145/1755913.1755940] |
| [13] | Ousterhout K, Wendell P, Zaharia M, Stoica I. Sparrow:Distributed, low latency scheduling. In:Proc. of the 24th ACM Symp. on Operating Systems Principles. ACM Press, 2013. 69-84.[doi:10.1145/2517349.2522716] |
| [14] | Ghodsi A, Zaharia M, Shenker S, Stoica I. Choosy:Max-Min fair sharing for datacenter jobs with constraints. In:Proc. of the 8th ACM European Conf. on Computer Systems. ACM Press, 2013. 365-378.[doi:10.1145/2465351.2465387] |
| [15] | Venkataraman S, Panda A, Ananthanarayanan G, Franklin MJ, Stoica I. The power of choice in data-aware cluster scheduling. In:Proc. of the 11th USENIX Symp. on Operating Systems Design and Implementation (OSDI 2014). 2014. 301-316. |
| [16] | Boutin E, Ekanayake J, Lin W, Shi B, Zhou J, Qian ZP, Wu M, Zhou LD. Apollo:Scalable and coordinated scheduling for cloud-scale computing. In:Proc. of the 11th USENIX Symp. on Operating Systems Design and Implementation (OSDI 2014). 2014. 285-300. |
| [17] | Tumanov A, Zhu T, Kozuch MA, Harchol-Balter M, Ganger GR. Tetrisched:Space-Time scheduling for heterogeneous datacenters. Technical Report, CMU-PDL-13-112, Carnegie Mellon University, 2013. |
| [18] | Goder A, Spiridonov A, Wang Y. Bistro:Scheduling data-parallel jobs against live production systems. In:Proc. of the 2015 USENIX Annual Technical Conf. (USENIX ATC 2015). 2015. 459-471. |
| [19] | Delimitrou C, Kozyrakis C. Paragon:QoS-Aware scheduling for heterogeneous datacenters. ACM SIGPLAN Notices, 2013, 48(4): 77–88 . [doi:10.1145/2451116.2451125] |
| [20] | Huang XL, Bensaou B. On max-min fairness and scheduling in wireless ad-hoc networks:Analytical framework and implementation. In:Proc. of the 2nd ACM Int'l Symp. on Mobile Ad Hoc Networking & Computing. ACM Press, 2001. 221-231.[doi:10.1145/501445.501447] |
| [21] | Goldberg AV. An efficient implementation of a scaling minimum-cost flow algorithm. Journal of Algorithms, 1997, 22(1): 1–29 . [doi:10.1006/jagm.1995.0805] |
| [22] | Dantzig GB. Linear Programming and Extensions. Princeton: Princeton University Press, 1963. . |
| [23] | Seref O, Ahuja RK, Orlin JB. Incremental network optimization:Theory and algorithms. Operations Research, 2009, 57(3): 586–594 . [doi:10.1287/opre.1080.0607] |
| [24] | Cherkassky BV, Goldberg AV. On implementing the push-Relabel method for the maximum flow problem. Algorithmica, 1997, 19(4): 390–410 . [doi:10.1007/PL00009180] |
| [25] | Reiss C, Wilkes J, Hellerstein JL. Google cluster-usage traces:Format + schema. Technical Report, Google Inc., 2011. http://code.google.com/p/googleclusterdata/wiki/TraceVersion2 |
| [26] | Firmament. Firmament quincy scheduler. 2015. http://firmament.io |
| [27] | Docker Swarm. Docker swarm filters. 2014. http://github.com/docker/swarm |
| [28] | Kubernetes. Kubernetes kube-schduler. 2014. http://kubernetes.io |
 2017, Vol. 28
2017, Vol. 28


