2015, Vol. 26
2. 北京邮电大学 智能通信软件与多媒体北京市重点实验室, 北京 100876;
3. 大连理工大学 机械工程学院, 辽宁 大连 116024;
4. 辽宁省先进设计与智能计算省部共建教育部重点实验室大连大学, 辽宁 大连 116622
2. Beijing Key Laboratory of Intelligent Telecommunications Software and Multimedia, Beijing University of Posts and Telecommunications, Beijing 100876, China;
3. School of Mechanical and Engineering, Dalian University of Technology, Dalian 116024, China;
4. Key Laboratory of Advanced Design and Intelligent Computing of Ministry of Education Dalian University, Dalian 116622, China
随着三维激光扫描技术的快速发展,三维数字几何模型已成为数字音频、数字图像、数字视频之后的第4种数字媒体形式,其相关基础理论和关键技术研究已经发展成为一门新的学科——数字几何处理,并逐渐在计算机辅助设计、动漫游产业、生物医药、数字文化遗产保护等领域取得了广泛的应用.面对海量的三维数字几何模型,如何进行精确有效地筛选与检索,已经成为了新的研究热点[1].
目前,多数的三维模型都是用于显示和绘制,往往只提供底层的基本几何属性和纹理外观属性,缺乏语义层的描述,导致三维模型的形状描述和检索难度要远远高于文本、图像及视频检索,三维形状的特征描述方法成为极具挑战性的难题.现有三维形状描述和检索技术可分为基于局部特征和基于全局特征两种类型:前者通过建立模型的多重局部特征,并根据特征对应关系寻找最优的匹配变换;后者将模型的内在特征压缩表示为一个特征向量或图结构,通过比较两个不同模型特征描述向量之间的相似测度来衡量两个模型之间的相似程度,常用的特征描述方法有形状分布直方图、傅里叶变换以及拓扑骨架信息等[2].
本文针对三维点云模型空间分布不均匀且无序的特征,首先构造其二维主流形,并以与球同胚的封闭网格形式给出主流形的二次曲面优化逼近,将三维点云模型的形状描述问题转换为球参数域上分布均匀、沿参数方向有序的二维主流形的参数化网格形状描述问题;然后,对二维主流形的参数化曲面网格进行三维平移、旋转和缩放等基本几何变换,对齐两个曲面流形网格的极轴,作为初始粗对齐;最后,基于迭代最近法向点(iterative closest normal point,简称ICNP)方法快速比较两个曲面网格流形,实现精准对齐,并将对齐误差作为两个三维点云模型的形状相似测度.实验结果表明:基于二次主流形网格的三维点云模型形状描述方法对分辨率变化、噪声、几何变化等因素具有较高的健壮性,可以有效地描述三维模型的整体形状特征.
1 相关工作 1.1 三维形状描述及检索三维形状检索对每个三维模型建立形状特征描述符,比较形状特征描述向量,得到模型之间的形状差异距离,以实现分类检索[3, 4].现有的三维形状描述方法可以分为基于直方图、基于变换、基于二维视角以及基于图等几类[5].
· 基于直方图的方法通过对模型的空间分布进行统计分析实现分类.
2002年,Zahari等人[6]提出三维霍夫变换(3D Hough transform,简称3DHT)特征描述符,可以保持模型内在拓扑不变性,并且采用空间对齐策略以保证几何不变性,分类效果较好,但是算法复杂度比较高.2007年,Fehr等人[7]提出基于具有旋转不变性的球面函数提取三维形状特征,并构造形状特征直方图,然后使用支持向量机(support vector machine,简称SVM)实现模型分类.2009年,Liu等人[8]通过对模型进行Monte-Carlo采样统计空间分布,并构造形状特征向量,基于Minkowski norns对形状特征向量进行相似度分析,实现了三维模型检索. Akgul等人[9]通过核深度估计优化了直方图描述符,并使用了采样多概率深度函数描述三维形状、实现模型检索.基于直方图的特征描述虽然易于实现,但仅使用统计信息描述模型特征,容易忽略模型细节,不具有足够的识别力.
· 基于变换的方法使用信号处理技术描述三维形状特征,例如傅里叶变换、球面投影等.
2009年,Papadakis等人[10]使用CPCA(constrained principal component analysis)及PCA(principal component analysis)保证模型的旋转不变性,并将模型用若干球函数表示,提高描述符的识别力,其效果优于光场描述符[11]. Tatsuma等人[12]提出多傅里叶光谱特征描述符,它是由4种独立的、带边缘增强的傅里叶光谱组成,可如实地捕获任意三维形状的固有特性而无需考虑模型的尺寸、方向以及初始位置,但四光谱叠加的最优权重比例未明确给出.2012年,Oliveira等人[13]通过构造三维模型的希尔伯特曲线,将三维形状描述降为一维的曲线形状特征描述,然后基于离散小波变换估测数对曲线进行采样,实现了对三维模型的形状描述.该方法具有低维度高精确性优点以及易于并行实现,但是对狭长以及有洞的模型健壮性不高.基于变换的特征描述符虽然对姿态变换具有一定的鲁棒性,但是获得姿态不变性的代价是丢失一些形状信息,易导致错误的检索.
· 基于二维视角的方法将三维模型视为若干二维图像的集合.
2010年,Papadakis等人[14]将三维模型投影到与模型主轴对齐的圆柱侧面获取三维模型的描述.与球谐函数相比,该特征描述符在欧式空间中的采样更加均匀.Shih等人[15]结合圆柱投影描述符和径向距离描述符,提高了检索准确性.2011年,Lee等人[16]结合高程值、径向距离、网格角度等3种投影特征描述符,每种投影特征都包含6个灰度图像,然后使用角度径向变换提取每个图像的特征向量,并实现了三维形状匹配.2012年,Tang等人[17]基于任意角度的视图特征对模型进行描述,并对视图特征进行聚类,通过样本训练确定正匹配和负匹配.该算法剔除了相机阵列设置的限制,增大了实验自由度.基于二维视角的特征描述方法虽具有较高的识别力,但是其舍弃了模型的三维信息,并且计算复杂度高.
· 基于图的方法通过建立模型的拓扑和几何特征来描述三维形状,更加直接具体.
2007年,Chaouch等人[18]在三维模型包围盒的6个投影平面上构造指定行列数目的深度线,通过深度线的空间姿态信息获取特征线队列,并将队列之间的海明距离作为三维模型相似度的衡量标准.2009年,Tierny等人[19]将每个模型提取附带几何属性的Reeb图,通过比较两个Reeb图的最大公共子图描述两个三维模型的局部形状相似性.该方法对于非刚体变换和噪声具有较高的健壮性.2011,年Shao等人[20]结合基于向量化轮廓的二维形状表示方法和基于采样的形状匹配策略,通过记录邻近点之间的变换,减少了采样配准的计算代价.不过,视点数量是否充分将影响最后的检索结果.2012年,Eitz等人[21]首先搜集了大量的骨架模型,然后基于Bag-of- Features方法构造模型的线条图,最后基于Gabor滤波器建立模型之间的变换,但是所收集到的骨架精准性难以保证.基于图的特征描述符可以描述模型的拓扑信息,但是难以获取且需要后续的图匹配操作,时间和空间复杂度较高.
1.2 主流形及应用主流形是嵌入高维空间的非欧氏低维流形,即点集的非线性主成分和子空间的概括.1984年,Hastie[22]将穿过数据中心的平滑曲线或曲面定义为主流形曲线或曲面,主流形上的每个点都是该点在原始点集中的局部平均.不同于其他的非线性扩展,主流形具有形式简单、自身一致性、几何解释清晰等特点.
对于r维随机变量P,其一维主流形定义如下:设G(l)={G1(l),G2(l),…,Gr(l)}是具有r个分量的向量函数,每一个分量都为参数l的光滑函数,将r维点集P投影到曲线G(l)中最近点,将投影指标记作:
lf(p)=maxl{l:||p-G(l)||=infm||p-G(m)||}.
从而,通过参数索引确定一维流形上的最近点信息.如果对于所有的l均有G(l)=E(P|lf(p)=l),其中,E为数学期望,则称G(l)为点集P的一维主流形,即主曲线.主曲线上的点可以视为所有投影点的平均,可以最小化重构误差:D2(P,G)=E(||P-G(& lt; span lang="EN-US" style='font-family:Symbol' xml:lang="EN-US">lf(P))||2),其中,D2(P,G)表示P与G之间的距离误差,||P-G(lf(P))||表示P和G(lf(P))之间的欧氏距离.
常用的线性降维方法PCA在处理多元正态分布的椭圆分布数据效果较好,但对一般的非线性数据结构的效果比较差,比如二次、三次或高次多项式数据;同时,线性的主成分分析受随机扰动的影响也比较大.而二次主流形作为非线性主成分分析方法,较好地回避了此类缺陷,并能够消除高维数据的统计冗余,降低了数据信息的损失.
主流形在一些领域应用比较广泛,例如分子生物学分析[23]、动态系统分析等.在文字检索处理方面,Sun等人[24]对比了3种不同主流形匹配算法在跨语言文本检索中的匹配效果,这3种方法都是将数据视为高维空间中的向量,通过主流体提取算法,将数据从不同的多重高维度空间嵌入到相同的低维度空间中,实现了不同类型的数据分类.He等人[25]针对图像和视频处理问题提出半监督降维方法MMP(maximum margin projection),该方法建立局部的主流形结构,对图像及视频进行降维,与待检索图像相似度高的图像在低维度空间中趋近于待检索图像,从而实现图像的检索.Chen等人[26]通过直方图估计和高斯混合模型估算视频队列的特征概率分布,提取概率特征分布主流形,将高维视频数据投影到低维空间,在低维空间比较映射队列实现视频的检索.在三维数字几何处理方面,Guskov[27]首先将输入模型分裂成多个Voronoi部分、建立参数化曲面,通过优化全局平滑函数生成最后的参数域,即主曲面参数域,最后对参数域进行重采样实现模型的重新网格化.
本文首先构造三维点云模型的二次主流形,并实现二次主流形的曲面网格逼近;然后,从距离、面积、平滑性这3方面优化主流形的参数化曲面网格;最后,基于极轴实现主流形曲面网格的粗对齐、基于ICNP实现主流形曲面网格的快速精准精对齐,并将两个主流形曲面网格间的配准误差作为三维形状的相似测度,实现了三维点云模型的形状描述.
2 主流形的曲面逼近及优化 2.1 二维主流形的二次曲面网格逼近Hastie[22]将主流形视为r维空间中的参数化流体,并分别定义了一维主流形和二维主流形.1997年,Kegl[28]采用了梯度优化算法提出了有长度约束的K主流形,并指出:如果数据点集存在有限的二阶矩,则其主流形一定存在.根据文献[4]可知,三维点云模型存在有限的二阶矩,故可以定义三维点云模型的一维主流形和二维主流形(或主曲面).
二维主流形由两个参数(l1,l2)控制生成,可表示为G(l1,l2)={G1(l1,l2),G2(l1,l2),…,Gr(l1,l2)},二维主流形上的点同样是原始投影点的局部均值,可最小化重构误差.对于三维点云模型输入的点集合P={pi,i=1,2,…,m},本文给出球形拓扑点云二维主流体的二次曲面逼近网格构建算法,描述如下[29]:
Step 1.对其进行主成分分析PCA,得到P的第一、第二和第三主轴Y1,Y2,Y3,以3个主轴为轴构建椭球面;
Step 2.以Y3与椭球的两个交点为极点,以Y1,Y2形成的主椭圆为赤道,以椭球面的经度和纬度方向为参数(l1,l2)的方向,沿(l1,l2)进行均匀的20x20采样;
Step 3.以20x20的采样点为结点集合V,在采样点间沿参数(l1,l2)方向顺次连接,构造边的集合,记作E,从而得到封闭的二维主流形的逼近网格MG,记为MG={V,E};
Step 4.将MG作为初始二维主流形的二次曲面网格逼近,调整MG得到优化网格逼近(见第3.2节).
2.2 逼近网格的优化对于主流形的初始网格MG={V,E},V={vi,i=1,2,…,t}为MG的结点集合,E={ei,i=1,2,…,s}为MG的无向边集合.设边ei的一个相邻边为ek,则定义结构Ri={ei,ek},将所有结构的集合记为R={Ri,i=1,2,…,r}.
对于给定三维模型,令其顶点集合P={pi,i=1,2,…,m},根据点pi距离MG上t个结点中的结点vi距离最近的分类原则,将集合P划分为t个子集,记为K={Ki,i=1,2,…,t},其中,Ki={pj:||pj-vi||≤||pj-va||,a=1,2,…,i-1,i+1,…,t;j=1, 2,…,m}.令:
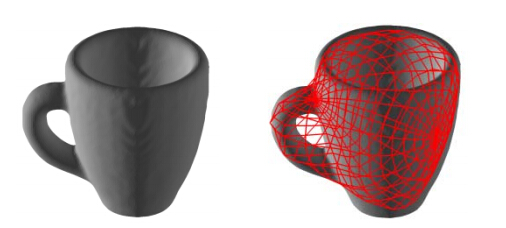 | Fig. 1 The left is the input model, and the right is the optimization approach of 2D manifold by quadric surface mesh图 1 左图为输入模型,右图为二维主流形的二次曲面网格优化逼近 |
三维模型的形状描述及匹配的实质是将多个局部空间的三维数据统一到世界坐标系中,然后,基于几何学与统计学的算法寻找模型之间的最优变换,以最小化模型点集之间的距离.本文将该匹配过程分为基于主流形极轴的粗对齐以及基于ICNP的精准对齐等两个步骤.
3.1 主流形网格的粗对齐粗对齐通过简单的平移、旋转和缩放等基本几何变化,简单快速地消除三维模型数据点集之间的位置和姿态差异,为后续基于ICNP的精准对齐提供好的初始条件,并降低ICNP的迭代次数、提对齐精准度.本文提出的二维主流形的逼近网格的拓扑结构为封闭的球形网格,故基于基本几何变化的粗对齐方法如下:
对于两个主流形的初始网格MG和${M'_G}$:
Step 1. 分别连接它们的两个极点p1和p2、${p'_1}$和${p'_2}$作为它们各自的极轴,记为L和L¢;
Step 2. 平移主流形网格MG,使其极点p1与${M'_G}$的极点${p'_1}$对齐;
Step 3. 旋转主流形网格MG,使其极轴L与与${M'_G}$的极轴L¢重合;
Step 4. 以p1为缩放中心、以L¢/L为缩放系数对MG缩放,使MG的极点p2与${M'_G}$的极点${p'_2}$重合.
至此,完成基于基本几何变换的主流形网格粗对齐.
3.2 基于ICNP的精准对齐主成分分析(PCA)以及迭代最近点(ICP)算法[30]经常用以解决三维模型的旋转、平移以及缩放不变性问题: PCA仅能够实现模型的粗略对齐,ICP算法则通过反复迭代、寻找待比较模型之间的最佳变换矩阵,但模型的初始位置对ICP算法的准确性有较大影响.ICNP算法是ICP算法一种改进,同样通过反复迭代以确定模型之间最佳刚性变换[31].与ICP不同,ICNP在寻找最近点时考虑法向夹角,迭代过程中利用了更多的几何信息,故所得的对齐结果更加精准.具体过程如下:
对于经过粗对齐的两个主流形网格MG和${M'_G}$,首先对MG中的每一个结点vi,在${M'_G}$中寻找与其欧式距离最小的点
,其中,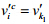
,这里,${k_1} = \arg {\min _{j \in [1,t]}}||{v_i} - {v'_j}||$;然后,在以为中心的邻域点集内,迭代寻找与vi法向夹角最小值的点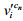
,其中,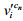$ = {v'_{{k_2}}},{k_2} = \arg {\min _{j \in \Omega }}(\arccos ({\alpha _i},{\beta _j}))$,W为相应邻域内的点在原点集${v'_i}$中的索引值集合,ai和bj分别为点vi和${v'_j}$的单位法向量,将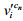记作vi的CNP(closest normal point).对MG进行平移旋转变换以减小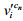和vi的距离总和,即最小化目标函数:
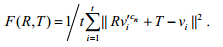
本文使用奇异值分解(singular value decomposition,SVD)计算最优旋转矩阵R以及平移矩阵T,使F(R,T)取得最小值[31].反复迭代此过程,直到两次迭代F(R,T)的差异小于一个阈值,迭代结束,算法取得了最优旋转矩阵R0和平移矩阵T0.
记d(MG,${M'_G}$)=F(R0,T0),令d(MG,${M'_G}$)为两个二维主流形的二次逼近曲面的形状差异测度,显然,d(MG,${M'_G}$) 越小,两个二维主流形之间形状差异就越小,对应的两个三维点云模型的形状相似度就越高.
4 实验结果与分析 4.1 实验环境本文的实验数据来自Princeton大学的三维模型数据库,选取茶杯、桌椅、鱼、汽车等48类共1 230个模型进行了实验.实验的软件环境是主频为2.4Ghz的Intel Xeon处理器、16GB RAM以及64位Windows 7操作系统,使用Matlab以及C++编程.本文根据检索评价基准,基于距离矩阵[32]、Tier图[32]、Precision-recall曲线[32]、GSS S曲线[33]、最近邻[32]、First tier[32]、second tier[32]、E-measure[32]、DCG[32]等工具对实验结果进行分析.
4.2 二维主流形的二次逼近网格部分三维点云模型的二次流形曲面逼近网格如图 2所示.显然:同一类模型的流形网格相似度较高,并且极轴长度也大体相近;而不同类别的模型之间,其流形网格的形状差别显著,极轴的长度和方向也存在明显差异.
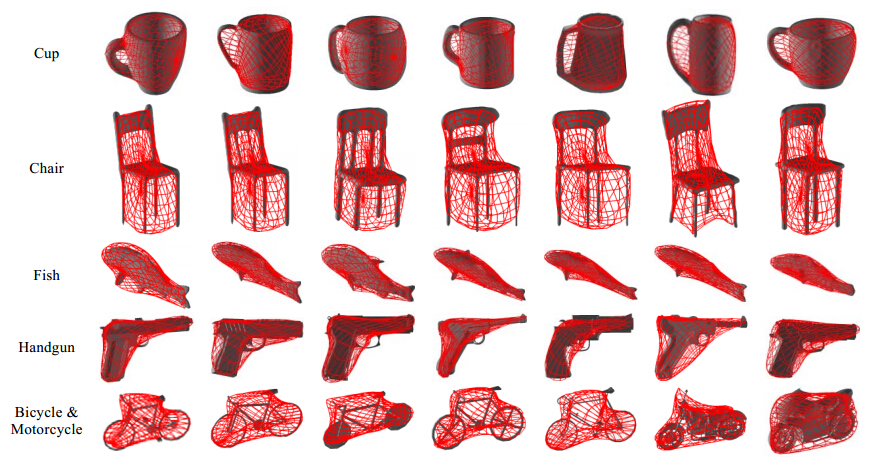 | Fig. 2 Results of some surface approximation mesh of their 2D manifold图 2 部分模型二维主流形的曲面逼近网格 |
为了验证本文二次主流形的曲面网格提取算法对噪声的健壮性,我们对输入点云模型上每个顶点的法向方向进行随机扰动,扰动角度区间为[0°,10°];同时,对每个顶点按照新的法向进行了位置扰动,扰动距离为[-d, d],d为最大扰动距离.按照最大扰动距离与模型最长轴比值的不同,分为3%,5%及10%等三级扰动,实验结果如图 3所示.图 4是同一个杯子模型、不同分辨率情况下的主流形网格曲面形状,图 4(a)~图 4(d)中,三维模型的顶点集合分别为1 000,4 000,8 000,10 000等不同的大小规模;图 4(e)是对模型进行旋转之后的主曲面形状.
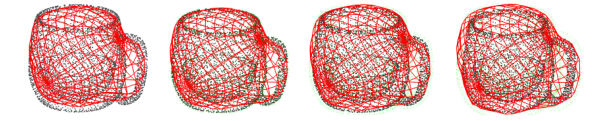 | Fig. 3 Noise test, from left to right is noise-free, with 3%, 5% and 10% noise respectively图 3 噪声测试,从左向右分别为无噪声、3%噪声、5%噪声以及10%噪声近网格 |
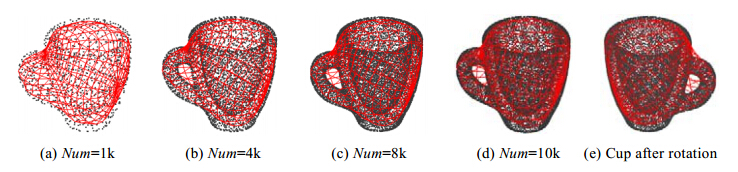 | Fig. 4 The surface approximation meshes of one cup with different resolution and pos图 4 不同分辨率及不同姿态Cup模型主流形的曲面网格逼近 |
表 1为图 4中模型与数据库中其他模型之间相似测度的距离矩阵.显然,本文算法对噪声干扰、细分和简化、以及旋转变换等情况具有较强的健壮性.
|
Table 1 The similarity measure d matrix of the models in Fig. 4表 1 图 4中的模型与其他模型之间相似测度d的矩阵 |
· 检索性能.
部分检索结果如图 5所示,左侧第1列为待检索模型,第2列~第11列为数据库模型按照与待检索模型之间相似测度d从左向右降序排列,模型下方的数字为该模型与待检索模型之间的相似测度d.显然,所有的待检索模型均被正确找出,并排在第1位,同类模型也排在靠前的位置.本文算法存在少量检索失败的情况,例如在第3行对自行车的检索结果中,由于四足兽模型具有相近的主流形网格外形而被错误检出.同样的情况也出现在第4行对鱼类检索时瓶子被错误检出,以及第8行对眼镜检索时四足兽和桌子被错误检出等;对于任意非零亏格的三维模型,本文算法计算所得的主流形曲面的亏格总为0,导致在模型细节信息方面有所丢失,对拓扑分支无法正确描述,今后的工作将充分考虑主流形的亏格特征,从而改善检测结果.
 | Fig. 5 Search results, ranked by the similarity in descending from left to right图 5 检索结果按照相似度从左向右降序排列 |
· 时间性能.
全部模型的主曲面拟合、特征提取工作在2.4Ghz的Intel Xeon处理器、16GB RAM的计算环境中平均用时为2.17s,对两个主曲面进行粗对齐以及精对齐操作平均用时为1.54s,其中大部分时间耗在基于迭代进行的ICNP精对齐步骤,粗对齐平均耗时不足0.01s.图 6是本文实验结果的局部Tier图[32],其中,第i行表示i模型的检索结果队列.点(i,j)位置上的色彩定义如下:如果模型i是模型j、或者为模型j的最近邻,那么该点显示为黑色;如果模型j在前N-1的匹配结果之中,则该点为第1层邻域;如果模型j在前& lt; /span>2x(N-1)个匹配模型之中,则该点为第2层邻域.图 6显示,在矩阵对角线处出现聚类现象、在远离对角线的位置上聚类情况较弱,这说明了本文算法在描述不同分类的三维模型上具有较高的类内相似性和较低的类间相似性.
 | Fig. 6 Tier matrix图 6 Tier图 |
我们将本文检索算法(principal manifold,简称PM)与相关性很强的调和形状直方图特征法(harmonic shape histogram,简称HSH)[7]以及形状投影特征法(projections of shape feature,简称PSF)[16]这3种算法的检索结果进行了对比,图 7给出了3种算法的PR(precision-recall)曲线,描述了查准率和查全率之间的关系.查准率是衡量检索系统的信号噪声比的一种指标,即,检出的相关模型与检出的全部模型的百分比;查全率是衡量检索系统从模型数据库中检出相关模型成功度的一项指标,即检出的相关模型与全部相关模型的百分比.PR曲线位置越高,则算法的检索性能越好.如 图 7所示:本文检索算法(PM)的检索结果要优于另外两种检索,在相同查全率的前提下,PM算法具有更高的检索精度.
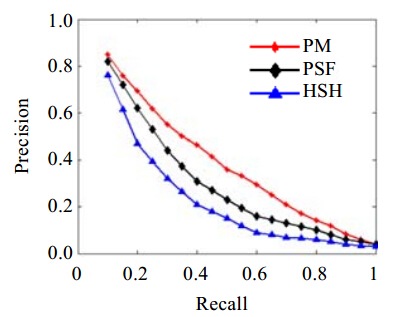 | Fig. 7 Precision-Recall curve图 7 Precision-Recall曲线 |
另外,基于GSSS(get score from similarity sequence)曲线评价标准对本文PM算法的检索结果的类间差异性和类内相似性进行了分析.与Shilane等人[32]以及Lin等人[33]的工作不同,本文没有基于形状对数据进行重新分类,避免了对数据语义信息的破坏.首先计算模型的类间相似度,考虑每个模型相似度最高的前10个检索结果并降序排列,根据文献[32]的记分规则,将每个队列的总分值并归一化至0~1之间,即为该模型的GSSS值.将所有模型的GSSS值按照升序排列,得到本文提出的PM算法、PSF算法以及HSH算法的GSSS曲线对比(如图 8所示),纵坐标表示该模型的GSSS值,横坐标表示经过排序后的模型索引.显然,本文提出的PM算法更能够区分两类模型之间的差异.
 | Fig. 8 GSSS curve 图 8 GSSS曲线 |
表 2是对PM,PSF和HSH等3种检索方法的定性分析评价,其中,E-Measure=2/(1/P+1/R)是查全率和查准率的复合评价,最大值为1.0,其值越大表示匹配结果越好.最近邻、第1层邻域、第2层邻域为Tier图中的概念,表 2中的最近邻一列的值为检索结果第1项(忽略待查询模型本身)与待查询模型为同类的比率,第1层、第2层的计算方法与最近邻相类似.DCG(discounted cumulative gain)统计衡量正确检索结果排在队列前端是否比排在队列后端多.显然,根据表 2的多种评价准则,PM方法仍然优于PSF方法和HSH方法.
|
|
Table 2 Qualitative comparison and analysis of three different search methods表 2 3种检索方法的定性比较分析 |
本文首先基于二维主流形的基本理论构造了三维点云模型主流形的曲面逼近网格,从而将空间分布的高度随机和高度不均匀的三维点云集合转换为二维主流形上与球面同胚的空间分布有序的、均匀的规则化参数分布,进而建立三维点云模型的形状特征描述;然后,基于简单几何变换粗对齐二维主流形的曲面网格极轴、并基于ICNP算法实现精准对齐,最终将对齐误差作为三维点云模型间的形状差异测度.实验证明:本文算法对噪声干扰、点云模型的不同尺度和空间姿态等因素具有较高的健壮性;与其他相关方法对比,本文算法的检索结果在查全率和查准率两方面表现更优,在Tier图、DCG等多种定量评价准则下,本文算法也表现出更好的性能,较好地实现了快速精准的三维点云模型形状特征描述和检索.
下一步将考虑对三维点云的二维主流形曲面网格进行优化,充分考虑非零亏格的流形特性,提出新的、更加突出局部形状特征的主流形表示,进一步提高三维形状特征描述和检索的精度和速度.
| [1] | Jayanti S, Kalyanaraman K, Iyer N, Ramani K. Developing an engineering shape benchmark for CAD models. Computer-Aided Design, 2006,38(9):939-953 . |
| [2] | Funkhouser T, Shilane P. Partial matching of 3D shapes with priority-driven search. In: Proc. of the 4th Eurographics Symp. on Geometry Processing. Eurographic Association, 2006. 131-142. |
| [3] | Tangelder JWH, Veltkamp RC. A survey of content based 3D shape retrieval methods. Multimedia Tools and Application, 2008, 39(3):441-471 . |
| [4] | Elad M, Tal A, Ar S. Content based retrieval of VRML object: An iterative and interactive approach. In: Proc. of the 6th Eurographic Workshop on Multimedia. New York: Springer-Verlag, 2001. 107-118 . |
| [5] | Daras P, Axenopoulos A. A 3D shape retrieval framework supporting multimodal queries. Int’l Journal of Computer Vision, 2010, 89(2-3):229-247 . |
| [6] | Zaharia T, Preteux F. Shape-Based retrieval of 3D mesh models. In: Proc. of the IEEE Int’l Conf. on Multimedia and Expo. IEEE Computer Society Press, 2002. 437-440 . |
| [7] | Fehr J, Burkhardt H. Harmonic shape histograms for 3D shape classification and retrieval. In: Proc. of the IAPR Conf. on Machine Vision Application. 2007. 384-387. |
| [8] | Liu ZB, Wang ZS, Zhang C. A novel 3D shape retrieval method using point spatial distributions along principal axis. In: Proc. of the Int’l Conf. on Information Management, Innovation Management and Industrial Engineering. 2009. 176-180 . |
| [9] | Akgul CB, Sankui B, Yemez Y, Schmitt F. 3D model retrieval using probability density-based shape descriptors. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2009,31(6):1117-1133 . |
| [10] | Papadakis P, Pratikakis I, Perantonis S, Theoharis T. Efficient 3D shape matching and retrieval using a concrete radicalized spherical projection representation. Pattern Recognition, 2007,40(9):2437-2452 . |
| [11] | Chen DY, Ouhyoung M, Tian XP, Shen YT. On visual similarity based 3D model retrieval. Computer Graphics Forum, 2003,22(3): 223-232 . |
| [12] | Tatsuma A, Aono M. Multi-Fourier spectra descriptor and augmentation with spectral clustering for 3D shape retrieval. The Visual Computer, 2009,25(8):785-804 . |
| [13] | de Oliveira WAA, Barcelos CAZ, Giraldi G, Guliato D. HSD: A 3D shape descriptor based on the Hilbert curve and a reduction dimensionality approach. In: Proc. of the IEEE Int’l Conf. on Systems, Man, and Cybernetics. 2012. 156-161 . |
| [14] | Papadakis P, Pratikakis I, Theoharis T, Perantonis S. PANORAMA: A 3D shape descriptor based on panoramic views for unsupervised 3D object retrieval. Int’l Journal of Computer Vision, 2010,89(2-3):177-192 . |
| [15] | Shih JL, Lee CH, Chou CH, Chang HY. A 3D model retrieval system based on the cylindrical projection descriptor. In: Proc. of the Int’l Conf. on Broadband, Wireless Computing, Communication and Applications. 2010. 550-555 . |
| [16] | Lee CH, Shih JL, Yu KM, Chang HY, Chiou YC. Projection of shape features for 3D model retrieval. In: Proc. of the Int’l Conf. on Multimedia Technology. 2011. 634-637 . |
| [17] | Tang J, Hong R, Yan S, Dai Q, Zhang N, Chua T. Camera constraint-free view-based 3-D object retrieval. IEEE Trans. on Image Processing, 2012,21(4):2269-2281 . |
| [18] | Chaouch M, Verroust-Blondet A. 3D model retrieval based on depth line descriptor. In: Proc. of the IEEE Int’l Conf. on Multimedia and Expo. 2007. 599-602 . |
| [19] | Tierny J, Vandeborre JP, Daoudi M. Partial 3D shape retrieval by reeb pattern unfolding. Computer Graphics Forum, 2009,28(1): 41-55 . |
| [20] | Shao T, Xu W, Yin K, Wang J, Zhou K, Guo B. Discriminative sketch-based 3D model retrieval via robust shape matching. Computer Graphics Forum, 2011,30(7):2011-2020 . |
| [21] | Eitz M, Richter R, Boubekeur T, Hildebrand K, Alexa M. Sketch-Based shape retrieval. ACM Trans. on Graphics, 2012,31(4): 31:1-31:10 . |
| [22] | Hastie T. Principal curves and surfaces [Ph.D. Thesis]. Stanford: Stanford University, 1984. |
| [23] | Gorban AN, Zinovyev A. Principal manifolds and graphs in practice: From molecular biology to dynamical systems. Int’l Journal of Neural Systems, 2010,20(3):219-232 . |
| [24] | Sun M, Priebe CE.Efficiency investigation of manifold matching for text document classification. Pattern Recognition Letter, 2013, 34(11):1263-1269 . |
| [25] | He X, Cai D, Han J. Learning a maximum margin subspace for image retrieval. IEEE Trans. on Knowledge and Date Engineering, 2008,20(2):189-201 . |
| [26] | Chen X, Hero A. Fisher information embedding for video indexing and retrieval. In: Proc. of the SPIE Electronic Imaging Conf. on Computational Imaging. 2011. 7873-7879 . |
| [27] | Guskov I. Manifold-Based approach to semi-regular remeshing. Graph Models, 2007,69(1):1-18 . |
| [28] | Kegl B, Krzyzak A, Linder T, Zeger K. A polygonal line algorithm for constructing principal curves. In: Proc. of the Neural Information Processing System. 1999. 501-507. |
| [29] | Zinovyev A. Method and software for fast construction of principal manifolds approximations. Technical Report, France: Institute of Advanced Scientific Studies, 2003. |
| [30] | Besl PJ, McKay ND. Method for registration of 3-D shapes. IEEE Trans. on Pattern Analysis and Machine Intelligence, 1992,14(2): 239-256 . |
| [31] | Mohammadzade H, Harzinakos D. Iterative closest normal point for 3D face recognition. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2013,35(2):381-397 . |
| [32] | Shilane P, Min P, Kazhdan M, Funkhouser T. The Princeton shape benchmark. In: Proc. of the Shape Modeling Applications. 2004. 167-178 . |
| [33] | Lin JJ, Yang YB, Lu T, Ruan JB, Wei W. A new performance benchmark for content-based 3D model retrieval. In: Proc. of the 9th Int’l Conf. on Web-Age Information Management. 2008. 285-292 . |